基于感应电势分解的永磁同步电机失磁故障诊断方法

杨 峰，杨永明

(重庆大学输配电装备及系统安全与新技术国家重点实验室，重庆 400044)

0　引言

在永磁电机永磁体生产材料的选择中，钕铁硼永磁材料的剩磁密度高、矫顽力大、磁能积大以及线性退磁曲线特性等优异性能使得其脱颖而出，是公认为非常适用于当作永磁体生产的磁性材料[1-2]。不过另一方面钕铁硼材料存在缺点，其磁性能受温度的影响比较明显，因此导致永磁体热稳定性能比较差、矫顽力具有负温度系数，温度较高时永磁体的磁性能将会下降[3]。随着电机运行温度的逐渐升高，永磁材料的磁性能将沿退磁曲线发生变化，在温度下降到正常以后永磁材料不会恢复原本磁性能，产生了一定程度的磁性能损失，当永磁体磁性能损失到达磁化曲线拐点时就会发生不可逆退磁，进而将会引起永磁电机的不可逆失磁故障[4]。在经过一批学者和一些机构多年的深入的研究，最近几年来针对永磁同步电机的失磁故障诊断主要有以下几个方面的成果：从电机设计方面的预防失磁设计[5-8]、在基于数学模型和有限元仿真模型方面的失磁故障模型研究[9-10]、采用多种信号处理提取失磁故障特征[11,12]以及在线监测方面的失磁故障检测与重构技术[13,14-17]。

本文最主要的研究目的在于对失磁故障下永磁同步电机定子齿磁通进行深入分析，根据数学模型发现失磁故障仅对故障磁极范围内的定子齿磁通转子分量有明显影响，于是采用探测线圈监测定子齿磁通分布，用探测线圈上的感应电势表示齿磁通，从而提出了一种基于感应电势分解的永磁同步电机失磁故障诊断方法。搭建了永磁同步电机局部失磁模型,并对诊断结果与仿真结果进行了分析对比，验证了诊断方法的有效性和正确性。

图1　定子绕组合成磁场示意图Fig.1 Schematic diagram of synthetic magnetic field of stator winding

1　永磁同步电机定子齿磁通数学模型

永磁同步电机定子齿中的磁通是由定子绕组产生的定子分量和永磁体产生的转子分量合成得到。为了便于理论分析，只考虑磁通的基波分量，并且不计铁心饱和程度的变化，在这种情况下，定子齿磁通是由定转子分量线性叠加得到。因此可对这两种分量分别计算。

1.1　定子齿磁通的定子分量

永磁同步电机定子绕组和传统交流电机类似，也是由对称的定子绕组构成。各项定子绕组中通入对称的电流，可以在电机内部合成一个随转子同步旋转的定子磁动势。对于常见的三相永磁同步电机，定子绕组产生的磁动势合成如图1所示。

旋转的磁动势会在每个定子齿上产生磁通。对于某一定子齿而言，磁动势的位置不同，产生磁通大小也不同。由于磁动势是同步旋转的，它和定子齿的相对位置随时间周期性变化，因此其在定子齿产生的磁通也是随时间周期性变化的。通常。定子齿磁通波形和定子磁动势位置之间的关系如图2所示。

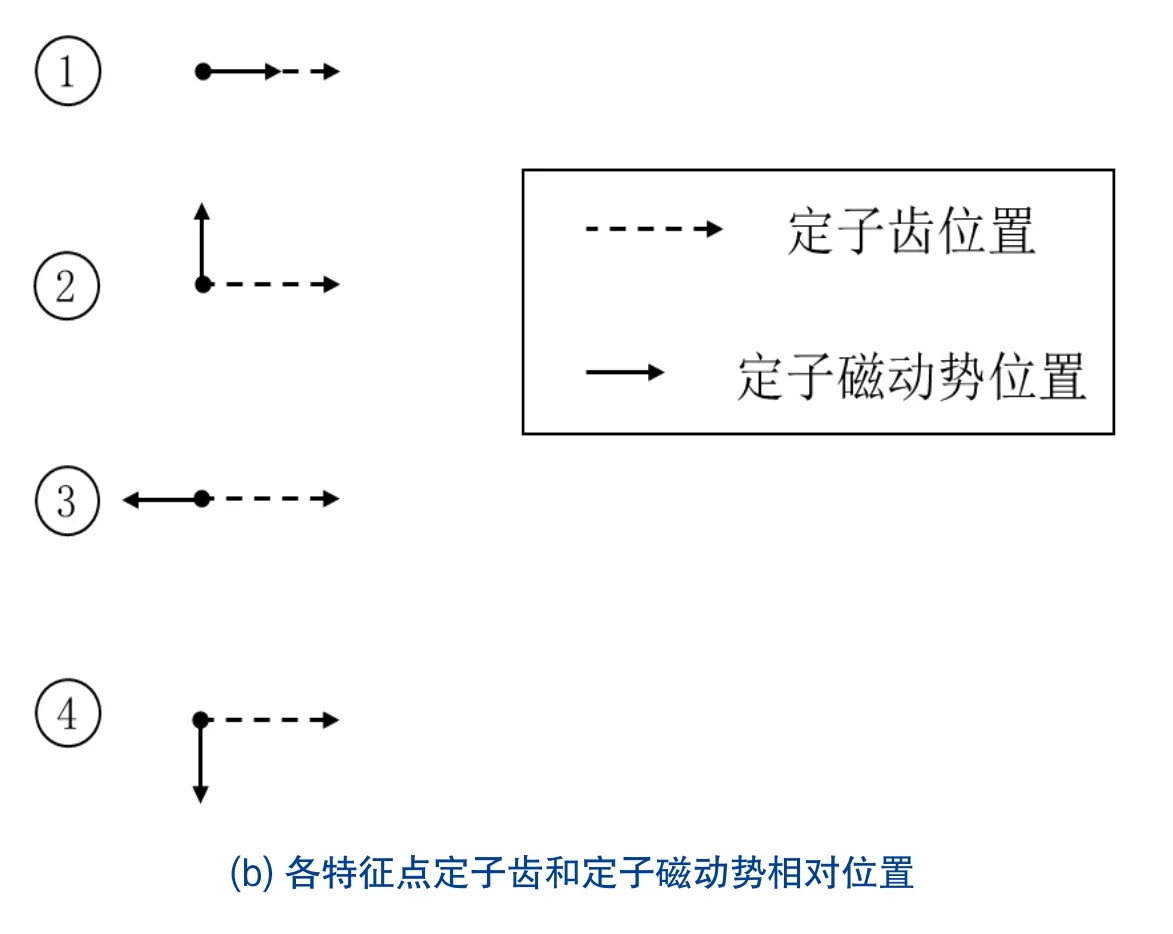
图2　定子齿磁通波形与对应的定子磁动势位置Fig.2 Stator tooth flux waveform and corresponding stator Magnetodynamic position

从图2可知，当磁动势方向和定子齿轴线重合时，定子齿磁通定子分量达到最大值；当磁动势方向和定子齿轴线夹角成90°时，定子齿磁通定子分量为零；当磁动势方向和定子齿轴线方向相反时，定子齿磁通定子分量达到负的最大值。

根据上述分析可知，定子齿磁通定子分量满足下式：

其中，是定子绕组产生的旋转磁动势相量，Rta是定子绕组产生的旋转磁动势在一个齿上产生磁通的等效磁阻,θa是定子绕组产生的旋转磁动势空间位置角（电角度），θt是定子齿轴线的空间位置角（电角度）。

以A相绕组轴线为参考位置(0°)，上式可以变换为：

其中，θA是A相电流相位。

根据上述推导可知，定子齿磁通定子分量的相位可由该定子齿和定子磁动势的相对位置确定。

1.2　定子齿磁通的转子分量

除定子分量以外，定子齿中的磁通还有转子分量，对于永磁同步电机而言，转子分量是由永磁体产生的。对于某一定子齿而言，磁通转子分量同样与定子齿和永磁体的相对位置有关，由于永磁体随转子同步旋转，引起磁通转子分量也是随时间周期性变化的。转子位置可以由d轴位置表示，定子齿磁通转子分量波形和d轴位置之间的关系如图3所示。

图3　转子齿磁通波形与对应的d轴位置Fig.3 Rotor tooth flux waveform and corresponding d axis position

从图3可以看出，当d轴和定子齿轴线重合时，定子齿磁通转子分量达到最大值；当d轴和定子齿轴线夹角成90°时，定子齿磁通转子分量为零；当d轴和定子齿轴线方向相反时，定子齿磁通转子分量达到负的最大值。

根据上述分析可知，定子齿磁转子分量通满足下式：

其中，是永磁体产生的磁动势相量，是永磁体在一个齿上产生磁通的等效磁阻，θf是d轴位置角（电角度）。

根据上述推导可知，定子齿磁通转子分量的相位可由该定子齿和d轴的相对位置确定。

1.3　失磁故障下的定子齿磁通

永磁体失磁后，其产生的磁动势大小和相位都会改变：

其中，Dd是失磁程度，用百分比表示，Δθf表示失磁故障对永磁体产生磁动势相位的影响。

通常一台永磁电机有多对永磁体磁极，根据失磁故障类型的不同，可能部分是部分永磁体失磁也可能是全部永磁体失磁。由于永磁体产生的磁场主要集中在磁极覆盖的范围以内。因此当电机发生失磁故障后，各定子齿磁通转子分量满足下式：

在不计铁心磁阻变化的假设下，失磁故障并不会影响磁通定子分量对应的磁路，因此失磁故障下磁通定子分量仍满足式(2)。

根据上述推导可知，发生失磁故障后，磁通定子分量、非故障磁极范围内磁通转子分量基本不变；失磁故障仅对故障磁极范围内的磁通转子分量有明显影响。

2　基于感应电势分解的失磁故障诊断方法

2.1　探测线圈的放置及工作原理

从上一节的分析可知，失磁故障对其范围内的定子齿磁通转子分量有明显的影响，因此可以利用这一特点对失磁故障进行诊断。为了实现这一想法，首先需要对定子齿磁通进行实时监测。

本文采用探测线圈对定子齿上的磁通进行实时监测。根据电磁感应定律，探测线圈上的电势和定子齿磁通满足下述方程：

其中，Ns是探测线圈的匝数，Uc是探测线圈上的电势。

显然，探测线圈上的电势和齿磁通的微分成正比，由于电机运行时齿磁通是周期性波动的，因此可直接用探测线圈上的电势表示齿磁通。

失磁故障主要是对转子分量的基波产生影响，因此本文仅对基波进行分析。失磁故障时探测线圈上的电势基波幅值可能随时间变化，因此采用短时傅里叶变换计算感应电势在一个周期内的平均基波幅值：

其中，T是同步电周期。

为了同时监测每个定子齿的磁通，在每个定子齿上都安装探测线圈，如图4所示。为了便于诊断时对故障位置的判定，安装时对每个线圈进行编号，并记录它们的位置。由于安装线圈需要重新绕制定子绕组，因此该程序适合在电机组装时同时完成。

图4　探测线圈位置示意图Fig.4 Schematic diagram of detecting coil position

2.2　感应电势分解与诊断方法

探测线圈上的感应电动势表示的是定子齿上的总磁通，在不计铁心饱和程度变化的假设下，感应电视同样可以分为定子分量和转子分量。下面，分别针对正常和失磁故障的情况进行分析。

(1) 正常工况

电机正常运行时，感应电势中定转子分量和磁通定转子分量满足下列方程：

图5　正常工况感应电势相量图Fig.5 Normal condition inductive potential phasor diagram

其中，ω是同步电角速度。

根据上述方程可知，正常工况下，感应电势及其各分量的向量图可以表示为：

从图5可以看出，感应电势可以分解为定、转子分量。实际中，的大小和相位可以根据实测波形利用信号变换得到。A相电流相位θA可根据实测电流波形计算得出，定子齿位置θt是一个常数可根据安装线圈时记录的位置得出。因此，可以根据定转子分量的相位对感应电势相量进行分解，从而得到定转子分量相量。

(2) 失磁故障

发生失磁故障时，故障范围外的感应电势仍满足式(9)和式(10)，故障范围内的感应电势定子分量也满足式(9)，转子分量满足下列方程：

正常工况和失磁故障范围内感应电势相量图对比如下：

从图6可以看出，失磁故障时，感应电势仍然由定子分量和转子分量构成。但是由于在实际中，无法得知失磁故障对转子分量相位的影响Δθf，因此无法按照该相量图对感应电势进行分解。

故障诊断的本质是在检测信号中分离出故障产生的信号，并根据故障信号对故障参数进行判断。从图6还可以看出，失磁故障对感应电势的影响都集中在转子分量部分，因此可以在失磁故障感应电势中分别减去正常运行时的定子分量和转子分量来获取失磁故障对感应电势的影响。

(3) 诊断方法

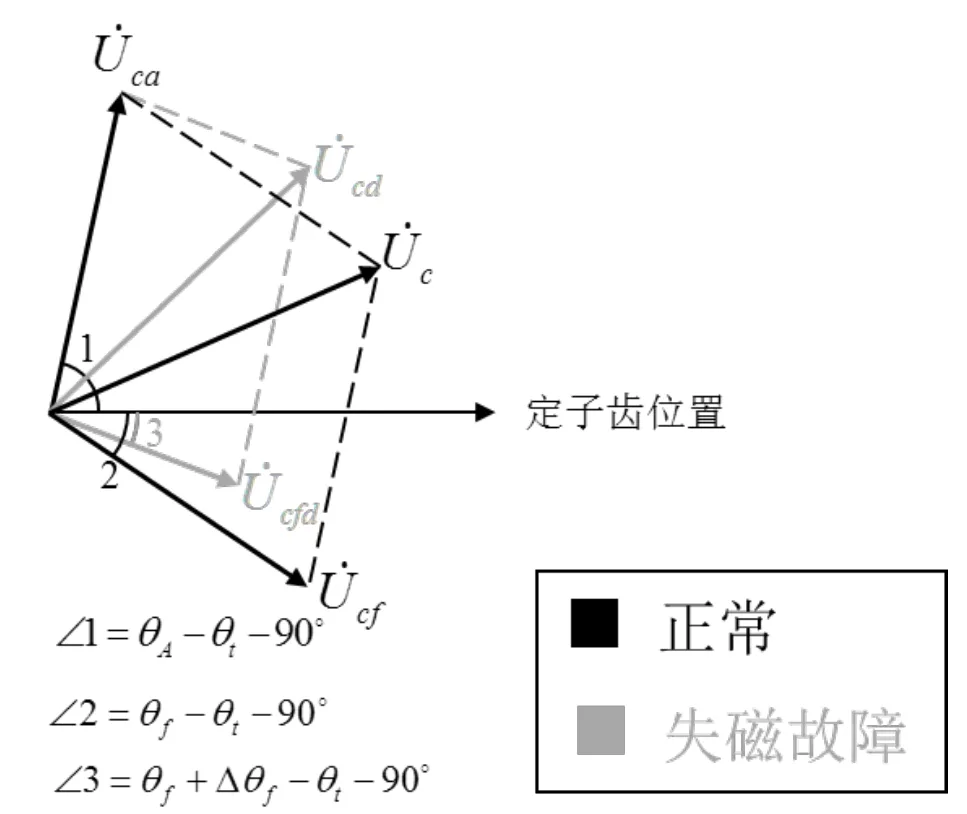
图6　正常工况和失磁故障范围内感应电势相量图Fig.6 Phasor Diagram of Induction potential in normal working condition and loss of excitation Fault range

基于上述分析可知，可以通过在实测感应电势中减去正常运行的定、转子分离来获取失磁故障产生的感应电势。为了实现这一想法首先需要获取电机在整个运行区间的定转子分量参考值；然后在实际监测时，根据电机工况（转速、转矩）在实测感应电势中减去相应的定转子分量；最后将各个定子齿所得结果进行汇总，并根据结果分布特性对失磁故障进行诊断。

具体而言，本文采用下述方法实现上文所述思想：

(1) 获取参考值

在作为参照的正常永磁同步电机的每一个定子齿上绕制探测线圈，尽可能对电机所有可能出现的工况下(不同转矩、不同转速)，提取每一个感应线圈上随时间变化的感应电势，并计算其在各个时刻的基波相量表示的幅值，θofai表示的相位，i为线圈的编号。

计算定子绕组在每一个该线圈产生感应电势的相位如下式：

其中是A相电流的相位，是A相绕组轴线与第i号线圈位置的电角度差。

计算永磁体在每一个线圈产生的感应电势相位如下式：

其中是d轴与第i号线圈位置的电角度差。

计算每一个线圈上由定子电流产生的感应电势参考值：

计算每一个线圈上由转子永磁体产生的感应电势参考值：

(2) 求取故障分量

提取故障永磁同步电机每一个感应线圈上随时间变化的感应电势，并计算其在各个时刻的基波幅值并计算其在各个时刻的基波相量表示幅值，表示的相位。选取与故障电机运行工况相对应的参考值，即同一转矩、同一转速下正常运行的电机的定子分量和转子分量按下式求得故障电机每一个定子齿上的探测线圈感应电势的故障分量：

(3) 故障诊断

将故障分量绘制成雷达图，利用故障分量雷达图分布情况诊断永磁同步电机失磁故障位置和失磁程度。为了便于区分由信号提取和分析计算过程中产生的误差值与故障分量，引入一个判断阈值TH，其计算公式如下：

a为阈值系数，取值与电机参数有关，根据本文所采用电机情况取值100。

若被监测永磁同步电机的所有线圈上的故障分量均小于阈值则电机正常；若雷达图上故障分量明显增大，且随电机旋转而变化，则判定为永磁体失磁故障，故障分量明显增大的位置就是发生失磁的位置，根据故障分量计算失磁程度。

3　诊断方法的仿真验证

为验证提出的诊断方法的有效性，本文在ANSYS Maxwell中搭建了永磁同步电机局部失磁模型，电机设计参数见表1。

表1　永磁同步电机参数Tab.1 PMSM parameters

3.1　诊断方法对失磁故障定位的诊断结果分析

根据搭建的局部失磁模型，设置3块永磁体失磁20%，电机的工况为转速3000 rpm、转矩40 Nm。图7为此时故障分量UF雷达图与故障永磁体该时刻所在位置对比图。

图7(a)中，三块失磁永磁体的位置覆盖在18号定子齿、1号定子齿、2号定子齿和3号定子齿；图7(b)中探测线圈感应电势的故障分量存在于18号线圈、1号线圈、2号线圈和3号线圈中，其幅值分布在0.375 V到0.625 V之间。可以看到，永磁体同步电机三块永磁体发生失磁故障时，故障分量在雷达图中出现的位置与失磁永磁体位置相同。因此，诊断方法对永磁同步电机局部失磁定位是准确的。

图7　三块永磁体失磁故障分量雷达图与故障永磁体位置对比图Fig.7 Comparison of fault component radar diagram and fault permanent magnet position when three block permanent magnet fault

3.2　诊断方法对失磁故障程度的诊断结果分析

分别设置失磁模型失磁10%、20%、30%、40%、50%、60%、70%、80%、90%，由仿真结果计算得出不同失磁程度下的故障特征量如图3.2所示。

图8可看出，当永磁体失磁程度为10%时，故障特征量在图中为最小值0.277 V；当永磁体失磁程度为90%时，故障特征量在图中为最大值3.39 V。而且还可以清楚的看到，故障特征量随着失磁程度增加而增大，且为良好的线性关系。因此，诊断方法对永磁同步电机的失磁故障程度诊断结果是准确的。

图8　失磁程度与故障特征量曲线图Fig.8 The curve of demagnetic level and fault characteristic quantity

综上，本文所提出的基于感应电势分解的永磁同步电机失磁故障诊断方法可以及时判断永磁体失磁位置和失磁程度，仿真结果验证了诊断方法的有效性和正确性。

4　结论

本文以内嵌式永磁同步电机作为研究对象，对永磁同步电机定子齿磁通分布、永磁体局部失磁磁场特征、失磁故障特征量提取及失磁诊断方法等几个方面进行了分析和研究，归纳总结如下：

1) 分别建立定子齿磁通定子分量数学模型和转子分量数学模型，并得出了永磁同步电机在各种工况（正常运行和失磁故障状态下）运行时的定子齿磁通计算公式。基于永磁同步电机定子齿磁通数学模型对失磁故障下定子齿磁通的分析发现，当永磁同步电机发生失磁故障时对故障范围内的定子齿磁通转子分量有明显的影响。利用这一特点，采用探测线圈对定子齿上的磁通进行实时监测，用探测线圈上的电势表示齿磁通，提出了一种基于感应电势分解的失磁故障诊断方法。

2) 基于ANSYS Maxwell软件建立了失磁故障仿真模型对诊断方法性能进行了评估，得出的结论是：故障分量所在雷达图中出现的位置能准确地对电机失磁位置进行定位；提取的故障特征量与永磁体失磁程度之间线性关系良好，诊断方法能正确的判断永磁同步电机的失磁程度。

[1] ZHILICHEV Y. Analysis of Permanent Magnet Demagnetization Accounting for Minor B-H Curves [J]. IEEE Transactions on Magnetics,2008, 44(11):4285-4288.

[2] 刘国征, 夏宁, 赵明静. 永磁材料长期稳定性研究进展[J]. 稀土, 2010, 31(2): 40-44.LIU Guo-zheng, XIA Ning, ZHAO Ming-jing. Progress in long-term stability of permanent magnet materials [J] . Rare Earth, 2010,31(2):40-44.

[3] BINNER A, ROTH S, STILLER C. Calulation of demagnetisation curvers of NdFeB-magnets using the finite-element-method[J]. IEEE Transactions on Magnetics Mag, 2002, 30(2): 622-624.

[4] 刘荣林. 永磁电动机失磁分析[J]. 中国民航大学学报, 2004, 22(s1):18-20.LIU Rong-lin. Demagnetism analysis of permanent magnet motor [J]. Journal of Civil Aviation University of China , 2004, 22(s1):18-20.

[5] XING J Q, WANG F X, WANG T Y, et al. Study on anti-demagnetization of magnet for high speed permanent magnet machine[J]. IEEE Transactions on Applied Superconductivity, 2010, 20(3): 856-860.

[6] YANG Y H, WU C J. Study of anti-demagnetization property for a flux-shunt magnet DCmotor[C]. IEEE International Conference on Industrial Technology, 2010: 422-426.

[7] JANG S M, PARK H L, CHOI J Y, et al. Magnet pole shape design of permanent magnet machine for minimization of torque ripple based on electromagnetic field thirty[J]. IEEE Transactions on Magnetics, 2011, 47(10): 3586-3589.

[8] HONG H, YOO J. Shape design of the surface mounted permanent magnet in a synchronous machine[J]. IEEE Transactions on Magnetics,2011, 47(8): 2109-2117.

[9] 钟钦, 马宏忠, 梁伟铭, 等. 电动汽车永磁同步电机失磁故障数学模型的初步研究[J]. 微电机, 2013, 46(6): 9-12.ZHONG Qin, MA Hong-zhong, LIANG Wei-ming, et al. A preliminary study on the mathematical model of magnetic failure of permanent magnet synchronous motor of electric vehicle[J]. Micromotors, 2013, 46(6): 9-12.

[10] URRESTY J C, RIBA J R, DELGADO M, et al. Detection of Demagnetization Faults in Surface Mounted Permanent Magnet Synchronous Motors by Means of the Zero-sequence Voltage Component[J]. IEEE Transactions on Energy Conversion, 2012, 27(1): 42-51.

[11] 李伟力, 程鹏, 吴振兴, 等. 并网永磁同步发电机转子永磁体局部失磁特征量的计算与分析[J]. 中国电机工程学报. 2013, 33(33): 95-105.LI Wei-li, CHENG Peng, WU Zhen-xing, et al. Calculation and analysis of the local magnetic loss characteristics of the rotor permanent magnet of a synchronous synchronous synchronous generator with mesh[ [J]. Journal of Chinese Electrical Engineering, 2013, 33(33): 95-105.

[12] URRESTY J C, RIBA J R, ROMERAL L. A Back-emf Based Method to Detect Magnet Failures in PMSMs[J]. IEEE Transactions on Magnetics, 2013, 49(1): 591-598.

[13] HONG J, HYUN D, SANG B L, et al. Automated Monitoring of magnet quality for Permanent Magnet Synchronous Motors at standstill[J].IEEE Transactions on Industrial Applications, 2010, 46(4): 1397-1405.

[14] DA Y, SHI X D, KRISHNAMURTHY M. A new approach to fault diagnostics for Permanent Magnet Synchronous Machines using electromagnetic signature analysis[J]. IEEE Transactions on Power Electronics, 2013, 28(8): 4104-4112.

[15] KIM K C, LIM S B, KOO D H, et al. The shape design of permanent magnet for permanent magnet synchronous motor considering partial demagnetization[J]. IEEE Transactions on Magnetics, 2006, 42(10): 3485-3487.

[16] HONG J, HYUN D, KANG T J, et al. Detection and classification of rotor demagnetization and eccentricity faults for PM synchronous motors[C]// Energy Conversion Congress and Exposition. IEEE, 2011:2512-2519.

[17] HOSOI T, WATANABE H, SHIMA K, et al. Demagnetization analysis of additional permanent magnet in salient-pole synchronous machines with damper bars under sudden short circuit[J]. IEEE Transactions on Industrial Electronics, 2012, 59(6): 2448-2456.