基于交织技术的最优低碰撞区跳频序列集
2018-04-04牛宪华胡梦婷西华大学计算机与软件工程学院四川成都610039
凌 龙,牛宪华,胡梦婷,吕 中(西华大学计算机与软件工程学院,四川 成都 610039)
跳频扩频是扩频通信中一种很常见的扩频方式,具有较好的抗干扰性、安全性、多址性,被广泛应用于蓝牙、军事通信、移动通信、雷达和声纳等系统[1-3]。所谓跳频就是利用伪随机序列来对数据调制的载波中心频率进行控制,使其按照一定的顺序和速率在一组频率中进行任意随机的跳变,相应地接收端也按照同样的顺序和速率来进行接收并且解调[4]。通常情况下在码分多址环境中,总是希望保持发射机之间的相互干扰在尽可能低的水平[5-8]。当2个或多个发射机同时在同一频率上传输时易发生相互干扰,相互干扰的程度和跳频序列的汉明相关性紧密相连;因此,设计具有良好的汉明相关特性的跳频序列(frequency hopping sequences,FHS)是研究跳频技术的重要内容。
2003年Ye等[9]首次提出低碰撞区/零碰撞区(low hit zone/no hit zone,LHZ/NHZ)跳频序列的概念。LHZ跳频序列是一种具有特殊性质的跳频序列,序列在LHZ的汉明相关性能决定了系统抗多址干扰的能力。有关LHZ跳频序列集(frequency hopping sequences sets, FHSS)构造的研究有重要意义并取得了一些成果[10-13],但现有成果中构造的序列集序列数目还不够大,不能充分利用带宽。本文基于交织技术构造得到了序列数目更大的最优低碰撞区跳频序列集。
1 预备知识
首先给出跳频序列汉明相关函数的定义。设F={f0,f1,…,fq-1}是一个大小为q的频隙集,S是由F上M个长度为N的跳频序列组成的集合。
定义1设频隙集F={f0,f1,…,fq-1},令x={x0,x1,…,xN-1},y={y0,y1,…,yN-1},(xi,yi∈F,i=0,1,…,N-1)为频隙集F上2个长度为N的跳频序列,x和y在相对时延τ的周期汉明互相关函数为

(1)
式中:i+τ按模N运算;当x=y时,H(x,y;τ)称为周期汉明自相关函数;当x≠y时,H(x,y;τ)称为周期汉明互相关函数。
对于已知的跳频序列集S,序列集的最大周期汉明自相关Ha(S)、最大周期汉明互相关Hc(S)和最大周期汉明相关Hm(S)分别定义为:
Ha(S)=max{H(x,x;τ)|x∈S,0<τ 简记为Ha=Ha(S),Hc=Hc(S),Hm=Hm(S)。 在2004年,Peng等[14]建立了FHSS的最大周期汉明相关值的下界。 引理1(Peng-Fan界) 令F是一个大小为q的频隙集,S为F上M个长度为N的跳频序列构成的集合,有 (2) 对于任意跳频序列集S,令整数Ha≥0,Hc≥0,F是一个大小为q的频隙集,S为F上M个长度为N的低碰撞区跳频序列构成的集合,那么S关于周期汉明相关函数的低碰撞区LH、自相关低碰撞区LAH和互相关低碰撞区LCH分别定义为: 当Ha=Hc=0时,LH称为S的零碰撞区,亦表示成NH。一个具有LH≥0(或NH≥0)的跳频序列集S称为LHZ FHSS(或NHZ FHSS)。有关LHZ或NHZ FHSS构造的研究有重要意义并取得了丰富的成果[15-18]。 在2004年,Peng等[19]推导了LHZ跳频序列集的周期汉明相关理论界。 引理2(Peng-Fan-Lee界) 令F是一个大小为q的频隙集,S为F上M个长度为N的跳频序列构成的集合,LH是序列集S关于周期汉明相关函数的LHZ。对于任意整数Z,0≤Z≤LH,有 (3) 在本文中:用(N,q,l,Hm)表示一个序列长度为N,频隙大小为q,序列数目为l,最大汉明相关为Hm的FHSS;用(N,q,l,L,Hm)表示一个序列长度为N,频隙大小为q,序列数目为l,LHZ为L,最大汉明相关为Hm的FHSS。 交织序列理论在1995年由Gong首先提出[20]。 设A={a0,a1,…,al-1}是一个(N,q,l,Hm) FHSS,e=(e0,e1,…,el-1)是ZN上长度为l的移位序列,则由序列a和移位序列e可以构成一个N×l的矩阵 其中下标按模N运算。把矩阵U中的元素按行读出,可以得到一个周期为Nl的序列u=(u0,u1,…,uNl-1)。将a称为基序列,e称为移位序列,u称为交织序列。矩阵U是序列u的矩阵表示。为了简化,把交织序列u表示为 u=I(Le0(a0),Le1(a1),…,Lel-1(al-1))。 其中I表示交织操作。令g=(g0,g1,…,gl-1)为ZN上长度为l的移位序列,可生成交织序列 v=I(Lg0(a0),Lg1(a1),…,Lgl-1(al-1))。 对于时延τ=lτ1+τ2(0≤τ1 Lτ(v)=I(Lτ1+gτ2(a),…,Lτ1+gl-1(a), Lτ1+g0+1(a),…,Lτ1+gτ2-1+1(a)), 那么交织序列u和v在时延τ时的汉明相关函数可以表示为 特别地,当τ2=0时,有 从式(5)和式(6)中,当且仅当τ2=0时,交织序列u和v是移位等价的,等式(7)成立。 ei-gi=ej-gj,0≤∀i,j (7) 定义2Zn上任意2个移位序列e=(e0,e1,…,el-1),g=(g0,g1,…,gl-1),若等式(7)不成立,则e和g被称为不等价移位序列。 引理3基于上述分析,如果交织序列u和v是循环不等价的,而且e和g是不等价移位序列,则Huv(τ)=lHm。 此节将基于上述交织技术构造具有新参数的最优LHZ FHSS。 设F={f0,,f1,…,fq-1}是一个大小为q的频隙集,LHZ FHSS的构造如下。 构造1最优LHZ FHSS的构造。 步骤1,选择一个在F={f0,,f1,…,fq-1}上的最优A(N,q,l,Hm), 步骤2,令M,w为2个正整数,且满足 构造移位序列集H={E,G},有 其中0 步骤3,构造最优LHZ FHSSS={SA,SB}。 L(j+2l-2)w+(2l-2)(ai)), 其中x=iM+j(0≤i L(j+r)w+r(al-1)), 其中 0≤j 证明 首先,根据交织技术的原理,得出S的序列长度为lN,频隙大小为q。 其次,序列个数MS表示为 MS=MA+MB=lM+((w-1)-(2l-2))M= (w-l+1)M。 证毕。 定理2构造1中,如果参数满足 则得到的FHSSS是最优的(lN,q,(w-l+1)M,l-1,lHm)FHSS。 证明 频隙集F的大小为q,令Z=LH。FHSSS的最大汉明相关 根据Peng-Fan-Lee 界,FHSSS的最优汉明相关Hmo应为 所以,当 (8) 成立时,有 因此当式(8)成立时,序列集S是最优的(lN,q,(w-l+1)M,l-1,lHm)LHZ FHSS。 证毕。 注1:在构造1中,发现有移位等价的情况,接下来将消除等价的移位性。 算法1 输入:常数w,M。 输出:移位序列集H。 步骤1,生成初始移位序列 步骤2,生成等价的移位序列 步骤3,生成不等价的移位序列,H′={E′,G′}。 对E={ej|0≤j 说明:对移位序列集E={ej|0≤j 下面给出一个实例。 例1选择一个(56,13,3,4)的FHSSA={a0,a1,a2}如下: a0={2,2,6,12,1,0,8,12,4,11,3,8,10,1,10,10,4,8,5,0,1,8,7,3,2,1,1,5,11,11,7,1,12,0,5,1,9,2,10,5,3,12,3,3,9,5,8,0,12,5,6,10,11,12,2,8}; a1={4,4,12,11,2,0,3,11,8,9,6,3,7,2,7,7,8,3,10,0,2,3,1,6,4,2,9,10,9,9,1,2,11,0,10,2,5,4,7,10,6,11,6,6,5,10,3,0,11,10,12,7,9,11,4,3}; a2={8,8,11,9,4,0,6,9,3,5,12,6,1,4,1,1,3,6,7,0,4,6,2,12,8,4,5,7,5,5,2,4,9,0,7,4,10,8,1,7,12,9,12,12,10,7,6,0,9,7,11,1,5,9,8,6}。 令M=4,w=14,得到移位序列集H={E,G},根据构造1的步骤2得到移位序列集E和G,为 根据构造1的步骤3,利用交织技术得到以下FHSSS: ⋮ ⋮ 根据汉明相关性的定义,得到最大汉明自相关和最大汉明互相关,如图1所示。当τ<3时,Hm=12,S是一个(168, 13, 48,2,12) FHSS。 注2:观察图1,S的最大汉明互相关最大为168,发生了移位等价的情况。 图1 S的最大汉明相关函数 接下来消除移位等价。根据文献[10]中的构造3方法,替换E的最后2列,得到新的移位序列E′,根据文献[11]中的构造2,修改G中的最后2列,得到移位不等价序列集G′,其中E′和G′矩阵表示为: 交织后得到不等价的移位序列集 ⋮ ⋮ 根据汉明相关性的定义,得到最大汉明自相关和最大汉明互相关,如图2所示。当τ<3时,Hm=12,S′是一个(168,13,48,2,12)FHSS,并且S′中所有序列是移位不等价的。 图2 S′的最大汉明相关函数 注3:观察图2,S的最大汉明相关小于序列长度,说明移位等价的情况已经被消除。 基于交织技术,本文提出一种新的构造方法,与文献[12]和[13]相比,该方法所构造出的序列集具有新的参数。本文构造的序列集,其序列数目比已有文献的序列数目更大,且所有序列都是移位不等价的。通过选择一些已知的最优FHSS,满足特定条件可以构造出最优的LHZ FHSS。通过使用不同的移位序列,可以构造出参数设置更灵活的LHZ FHSS。该FHSS可以应用到准同步的跳时/跳频码分多址系统中,用于消除多址干扰。 [1]梅文华,杨义先.跳频通信编码地址理论[M].北京:国防工业出版社,1996. [2]赵寰, 全厚德, 崔佩璋. 抗跟踪干扰的多序列跳频无线通信系统[J]. 系统工程与电子技术, 2015, 37(3):671. [3]牛宪华,陈思利,王瑜. 跳频序列研究综述[J]. 西华大学学报(自然科学版),2016,35(2):259. [4]梅文华,王淑波,邱永红.跳频通信[M].北京:国防工业出版社,2005. [5]朱永松,张海勇,汲万峰. 跳频通信抗干扰性能分析[J]. 现代防御技术, 2005, 33(5):37. [6]苑雪, 曾兴雯, 申振宁. 跳频同步信号的干扰研究[J]. 西安电子科技大学学报(自然科学版), 2004, 31(6):896. [7]滕振宇,冯永新.差分跳频通信抗干扰效能分析[J].火力与指挥控制, 2012, 37(1):11. [8]牛宪华,曾柏森. 低碰撞区跳频序列平均部分汉明相关理论界研究[J]. 西华大学学报(自然科学版),2014,33(3):1. [9]YE W X, FAN P Z. Two class of frequency-hopping sequences with no-hit zone[C]//Proceedings of the Seventh International Symposium on Communications Theory and Applications (ISCTA’2003). Ambleside, UK:[s.n.], 2003:304-306. [10]LIU X, PENG D. Frequency hopping sequences with optimal partial Hamming correlation by interleaving techniques[C]//International Workshop on Signal Design and ITS Applications in Communications. Tokyo, Japan:IEEE, 2014:158-161. [11]XU Shanding,CAO Xiwang,XU Guangkui. Recursive construction of optimal frequency-hopping sequence sets[J]. IET Communications, 2016, 10(9):1080. [12]NIU X H, PENG D Y, ZHOU Z C. New classes of optimal low hit zone frequency hopping sequence with new parameters by interleaving techniques [J]. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Science, 2012, E95-A (11):1835. [13]NIU X H, ZHOU Z C. New classes of optimal low hit zone frequency hopping sequences with new parameters[J]. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Science, 2014, E97-A (12): 2567. [14]PENG D Y, FAN P Z. Lower bounds on the Hamming auto and cross correlations of frequency-hopping sequences [J]. IEEE Trans Inform Theory,2004, 50(9): 2149. [15]WENPING M S. New designs of frequency hopping sequences with low hit zone[J]. Designs, Codes and Cryptography, 2011, 60(2): 145. [16]HAN Y K, YANG K. New near-optimal frequency-Hopping sequences of length pq[C]//International Symposium on Information Theory. Toronto, ON, Canada:IEEE, 2008:2593-2597. [17]CHUNG J H, GONG G, YANG K. New families of optimal frequency-hopping sequences of composite lengths[J]. IEEE Transactions on Information Theory, 2014, 60(6):3688. [18]HAN H, PENG D, PARAMPALLI U. New sets of optimal low-hit-zone frequency-hopping sequences based on m-sequences[J]. Cryptography & Comm, 2016,9(4):1. [19]PENG D Y, FAN P Z, LEE M H. Lower bounds on the periodic Hamming correlations of frequency hopping sequences with low hit zone [J].Science in China Series F: Information Sciences,2006, 49(2):208. [20]GONG G. Theory and applications of q-ary interleaved sequences [J]. IEEE Trans Inform Theory,1995, 41(2):400.


2 交织序列理论
3 最优低碰撞区跳频序列集的构造
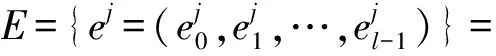


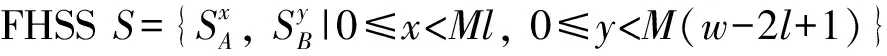

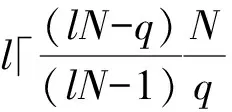
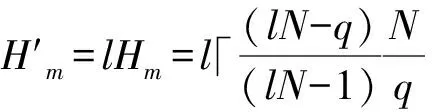

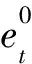
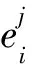






4 结论
