T字形钢箱梁异形块设计及空间受力特性研究

刘建威，于鹏，李德建

(1. 长沙市规划设计院有限责任公司，湖南 长沙 410007；2. 中南大学 土木工程学院，湖南 长沙 410075)

为顺应日益复杂的城市交通，异形桥梁成为城市立交的重要组成部分，尤其在车站、机场等大型交通枢纽的附属道路工程设计中更为常见。这类场地的路线设计常受限于施工条件及跨越能力的影响，而钢箱梁桥由于其结构自重轻、建筑高度小、受力性能好、制作精度高和施工周期短等优点，已成为复杂异形桥梁的结构形式之首选[1]。然而异形桥梁自身的力学特性较普通的直线桥、曲线桥更为复杂，且钢箱梁又为典型的空间薄壁构件，在偏心荷载下，会产生纵向弯曲、扭转、畸变和横向挠曲等变形，引发明显的弯扭耦合效应[2−4]，因此，钢箱梁异形块即便由恒载引起的应力和反力分布也较为复杂，实际中便曾出现对其受力情况掌握不全面而引发的的疲劳破坏、支座脱空等事故。针对异形桥梁的计算问题，设计中常用的分析方法有以下3种：1)根据结构特征和车道布载将异形块划分为各自独立的桥梁结构，从而采用平面梁单元分别进行建模计算，然而该方法忽略了各车道和各桥梁结构间的相互影响[5]；2)根据剪力柔性梁格理论对异形块进行结构离散，采用空间梁单元建模分析，该方法难以准确模拟薄壁结构的扭转、畸变及剪力滞效应，尤其对于曲率半径较小的异形结构，用梁格法计算各腹板分配内力时会引起较大误差[6−7]；3)采用板壳或实体单元建模计算，该方法建模过程相对复杂，后处理工作量较大，对于混凝土结构难以直接给出内力，但对于钢结构可以很好地进行构件设计和验算。随着通用有限元程序的发展，基于平面应力与弯曲复合的板壳元分析异形桥梁已是一种趋势[1,8]。因此为全面掌握钢箱梁异形块的空间受力特性，有必要采用板壳单元进行精细化建模分析，确定出结构在最不利工况之下的最不利部位，尤其是支座处的局部应力，这在桥梁设计和施工中既具理论价值又含现实意义。既有异形桥梁的研究多集中在 Y字形混凝土桥的梁格法分析方面[1,9]，基于板壳单元分析T字形钢箱梁异形块的文献仍旧较少。故本文以长沙市红旗路主线 65号~68号墩钢箱梁异形块为例，采用MIDAS/Civil考虑剪切变形的厚板单元进行全桥空间精细化仿真建模，以减少传统简化计算时因自由扭转假设、边界条件假设及横向尺寸效应假设等所引起的失真，从而对其空间受力特性进行更为可靠的分析，研究其在不同荷载作用之下的结构位移、截面应力、支座反力、自振特性及局部屈曲情况，为今后类似桥梁的设计计算提供参考。

1　钢箱梁异形块设计

1.1　工程概况

红旗路主线65号~68号墩钢箱梁异形块位于长沙火车南站东广场，该处道路交叉口为一T字形结构，南北主线为双向四车道，往进站口支线为双车道行车。该桥上部结构采用连续钢箱梁，南北向全长81 m，跨径布置为(32+15+34) m，东西向全长56 m，曲率半径最小至36 m，南北向桥宽16~20 m，东西向最小桥宽为9 m。本桥施工方法采用节段预制、现场支架拼装。

全桥平面布置如图 1。图中支座由南向北编号为65号~68号，自东向西按a，b，c和d编号，其中66号墩a支座为固定支座。图中Ⅰ-Ⅰ截面代表东西支线中跨跨中截面，Ⅱ-Ⅱ截面代表南北主线边跨跨中截面，A~F点分别代表对应截面上缘中点附近和外边缘处的点。

图1　T字形钢箱梁异形块平面布置图Fig. 1　Sketch map of plane layout of special T-shaped block of steel box girder

1.2　设计荷载

该桥主要设计荷载如下：

1) 恒载：Q345D钢材容重 78.5 kN/m3，护栏7.5 kN/m，沥青混凝土容重24.00 kN/m3，C50混凝土容重24.00 kN/m3。

2) 汽车荷载：城-A级，由于该处车流量较大，故不考虑横向折减效应。

3) 支座沉降：考虑纵横向的不均匀沉降，按单个支座处沉降5 mm考虑。

4) 局部温差：按升温14 ℃、降温7 ℃计。

1.3　设计细节

1.3.1截面总体设计

本钢箱梁异形块采用单箱多室截面，为尽可能合理地利用材料，在确定腹板间距时，综合考虑翼缘板有效宽度和正交异性钢桥面板的跨径来共同确定[10]。本桥梁高取为1.8 m，箱梁顶板采用闭口加劲肋，根据《公路钢结构桥梁设计规范》(JTG D64—2015)，横隔板的间距不宜大于4 m，即正交异性钢桥面板的跨径为不超过4 m。根据日本规范《道路桥示方书》对主梁有效宽度的规定，当连续梁单侧翼缘宽度小于跨径的1/20时，桥梁全跨度范围内翼缘全宽有效[11]。故本桥南北主线最终采用单箱五室截面，每个箱室宽度 3.2 m，左右侧悬臂长度均取2 m，桥梁其余部位通过加设横隔板使得各项参数取值均不大于以上。

1.3.2顶底板设计

为避免顶底板刚度过小导致的桥面铺装破坏，同时防止轮压荷载下产生局部屈曲，钢箱梁顶板厚度一般不小于12 mm，底板厚度不小于10 mm[12]。考虑到异形块的结构受力复杂和使用安全需求，本桥全桥顶板厚度取为27 mm，底板厚度为22 mm。为承受连续梁中间墩支座处产生负弯矩带来的压应力，并减小支座附近应力集中的影响，在支座两侧范围内将底板加厚至40 mm。

1.3.3横隔板设计

横隔板的设置会较大地影响钢箱梁的受力形态，一般横隔板厚度取为16 mm，支点处横隔板则加厚至32 mm，以起到局部加固作用，并较好地保证腹板通过横隔板将力传给支座[12]。设计中应注意合理布置横隔板间距，以尽量保证足够的施工作业空间。对于本钢箱梁异形块，由于结构线形限制难以保证横隔板按规律等间距布置，一般在跨中附近间距取为2.5~3.0 m，支座附近加密至2 m左右。

1.3.4纵向加劲肋设计

本钢箱梁异形块的顶底板宽度较大，为防止顶底板在使用阶段或者施工制作、运输、安装架设中不可预料的作用下发生局部失稳，设置纵横加劲肋是最有效的方法[13]。闭口截面加劲肋具有更大的抗扭刚度和屈曲稳定性，由于顶板承受汽车局部轮压，为提高桥面板刚度，选用10 mm厚的U形闭口纵肋；而底板主要承受拉应力，除在支座处设置局部加劲肋外，其余部位采用Ⅰ形开口纵肋，板厚约11~25 mm[14]，本桥取为20 mm，并保证顶板U形肋中心距不大于500 mm，底板I形肋中心距不大于450 mm。以68号墩顶处截面为例，最终确定的截面尺寸如图2。

图2　68号墩处横断面示意图Fig. 2　Sketch map of cross section of 68# pier

2　有限元模型的建立

2.1　单元选用

钢箱梁异形块结构复杂，且本桥汽车荷载和恒载相差不大，在各种荷载工况(尤其是偏载)作用下，会产生较大的约束扭转、畸变效应，全桥空间效应明显，局部容易产生应力集中和屈曲失稳，采用梁单元不能很好的模拟钢箱梁的细部结构，对于局部的变形失稳等情况的研究更不方便，而钢箱梁主要由顶板、底板、腹板、横隔板和纵横向加劲肋构成，其各组成部分均属于典型的薄壁构件，特别适合用板壳单元进行仿真建模，故本文采用 MIDAS/Civil中考虑剪切变形的板单元建模分析，该单元是基于Mindlin- Reissner板理论[15]建立的，每个节点包含6个自由度，属于小挠度弹性板单元，能较好地解决平面压缩、平面张拉、平面剪切及平板沿其厚度的剪切和弯曲等力学问题。由于本桥部分构件钢板厚度达到40 mm，其横向剪切应力也会对变形产生较大影响，故选用厚板单元进行建模。

2.2　模型建立

本文建模及分析的关键点如下：

1) 结构模拟：桥梁的平竖曲线、腹板和横隔板的尺寸和位置完全与施工图纸一致；支座加劲肋也采用厚板单元模拟，纵横向加劲肋则等效计入顶底板的厚度内；不考虑钢箱梁的制作过程中产生的残余应力和初始几何缺陷的影响。

2) 网格划分：采用混合网格划分，其中四边形单元用作全桥结构的主要单元，以避免三角形单元可能带来的较大应力计算误差；三角形单元则在不同尺度单元间起过渡作用，主要出现在结构曲线轮廓处，以及支座处顶底板等因为应力集中需要进行网格细分的部位。

3) 约束处理：固定支座处采用面支承，约束3个方向的线位移；活动支座也在支座支承面内约束竖向位移，并按实际布置情况施加水平方向的约束。

4) 荷载施加：桥面铺装按面荷载均匀施加在顶板单元上；防撞栏杆重量则视为线性均布荷载，施加在箱梁翼缘外边界单元上；车道荷载则按空间影响面进行加载，以准确模拟活载实际的作用效应。

5) 工况考虑：恒载(自重和二恒)、汽车活载(考虑车道满载和东、西、北侧偏载四种情况)、温度荷载和支座沉降。其中车道东、西侧偏载的加载方式如图3所示。各工况按相应规范在最不利的情况下进行组合，取其效应最大值，得出结构位移、反力、内力、应力等效应的包络值。

全桥共36 384个单元，31 564个节点，桥梁有限元模型及细部网格划分如图4所示。

图3　车道荷载加载示意图Fig. 3　Loading sketch map of lane load

图4　T字形钢箱梁异形块空间有限元精细化模型Fig. 4　Spatial FEM model of special T-shaped block of steel box girder

3　计算结果及分析

3.1　结构变形

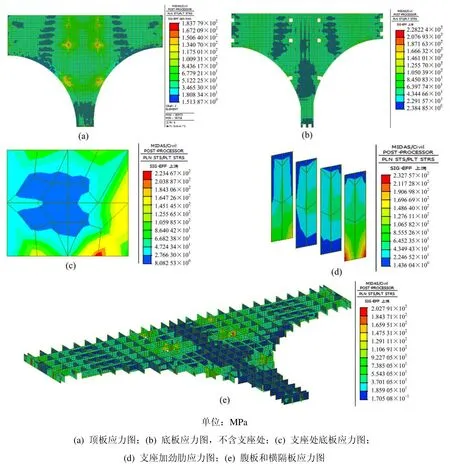
板单元模型能计算得出全桥任意位置的挠度分布，在恒载和1/2汽车活载作用下，钢箱梁顶板的竖向位移如图 5。可知，桥梁顶板内最大竖向位移出现在南北主线 65号~66号墩跨中截面外边缘处，其值为19.4 mm

图5　恒载+1/2汽车活载作用下主梁竖向位移Fig. 5　Vertical displacement under the action of dead load and half of vehicle load

边跨和中跨跨中截面各点位移如表 1所示(表中A~F点位置见图1)。可知在车道满载作用下，钢箱梁竖向位移最大值为17.49 mm

表1　钢箱梁桥竖向位移(以向下为正)Table 1　Deflection of steel box girder bridge (down direction is positive)　mm

3.2　 结构应力

在各种最不利工况基本组合下，钢箱梁顶底板最大Mises应力见图6(a)~6(b)。可知，顶底板等效应力除局部出现应力集中导致应力较大外，其他区域应力水平不高，均小于Q345D钢材设计强度值。顶板出现的应力最大值为183.8 MPa，不含支座加强板的底板最大应力为228.2 MPa，均出现在66号墩b支座附近，但面积较小。故设计中应对该部位构件进行适当加强，本桥支座处钢板厚度已加厚至40 mm，并设置了支座加劲肋。

钢箱梁局部构件最大Mises应力如图6(c)~6(e)所示，可见在支座横隔板、支座加强板和支座加劲肋处也出现了应力集中现象，应力最大值达到232.8 MPa，已接近钢材抗拉强度设计值260 MPa。但其面积很小、变形也很小，且发生在局部构件连接的地方，原因是由于多个板块相交时产生的局部应力集中，故在设计时应采取有效的方式减小和避免其带来的不利影响。

图6　基本组合下T字形钢箱梁异形块应力云图Fig. 6　Stress map of special T-shaped block of steel box girder under the basic combination

3.3　支座反力

由于该桥具有明显的空间效应，为了准确验算支座反力，各种荷载工况按最不利进行组合，各支座竖向反力根据支承面内节点反力计算合力而得，其结果如表2。可见，全桥最大支反力出现在66号墩b支座处，其值为9 377 kN，已接近该处所采用的GPZ 10000SX支座承载力设计值；全桥支座未出现脱空现象，最小支反力出现在66号墩d支座处，此时仍有952 kN的压力储备。进一步比较可知，T字形钢箱梁异形块的支反力不均匀现象明显，全桥具有显著的空间效应。其中66号墩和67号墩的a和b支座反力差值最大，分析可知，一是两处支座的荷载分担情况有较大差别，二是因为该处支座对约束主梁的扭转变形起较大的贡献作用。

3.4　结构自振特性

本文结构模态分析采用Lanczos法，计算得其前五阶自振特性结果如表3，对应的振型图如图7。由表可知，MIDAS板单元模型计算得本桥的基频为6.313 Hz，该桥一阶振型为南北线65号~66号跨竖向弯曲。由振型图可知，弯扭耦合效应对该桥振型具有较大的影响，设计中应引起重视，避免桥梁自振基频过低引发车桥耦合共振现象。

表2　支座竖向反力汇总表Table 2　Summary sheet of end reaction kN

表3　自振特性计算结果Table 3　Result of natural vibration calculation　Hz

图7　T字形钢箱梁异形块结构自振振型Fig. 7　Natural vibration modes of special T-shaped block of steel box girder

3.5　局部屈曲分析

为准确求出钢箱梁异形块局部构件在车辆荷载作用下的屈曲临界荷载，以横隔板为例，在全桥模型中对其进行弹性屈曲分析。选取支座反力最大处的66号墩横隔板为研究对象，考虑一排后轮(轴重为140 kN)的集中力作用在66号墩b支座附近，计算过程中采用两种模型进行比较，荷载的加载方式见图8：

模型1，不考虑混凝土桥面板影响的全桥模型；模型2，考虑混凝土桥面板(采用实体单元模拟)影响的全桥模型。

图8　车轮荷栽加载示意图Fig. 8　Sketch map of wheel load

66号墩横隔板在全桥模型中的弹性屈曲特征值分析结果如表4所示。可知，模型1的屈曲特征值为50，说明钢箱梁顶板将腹板和横隔板连成了一个整体，对车辆轮载起到了分散作用；比较模型 1和模型2的结果可知，钢筋混凝土桥面板大大增大了异形钢桥的刚度，使得荷载分配更为均匀，且 2种情况下特征值均大于 4，可认为横隔板在车辆荷载作用下有足够的安全系数[6,16]，不会发生屈曲。

表4　横隔板弹性屈曲特征值Table 4　Eigenvalues of diaphragm in elastic buckling analysis

4　结论

1) T字形钢箱梁异形块适合用于大型交通枢纽的设计中，但其结构受力复杂，活载分布情况多变，采用梁单元分析存在较大误差，设计中应尽可能地选用板壳或实体单元进行精细化建模，通过空间影响面加载对各种可能出现的活载分布情况进行分析，以全面掌握其空间受力特性，尽可能地减小结构空间效应带来的不利影响，防止过大的应力集中和支座脱空现象出现。

2) 该桥空间效应明显，即使在恒荷载作用下，钢箱梁同一截面顶缘中心处和外边缘的位移仍有较大差别；当发生车道偏载作用时，这种效应最为明显，A和B点最大位移差达到14.55 mm。此外B点竖向位移一直保持在1 mm左右的水平，这也是由于该类结构的空间效应导致的。

3) 该桥支反力不均匀现象明显，其反力值受纵横向荷载的分布情况影响较大。全桥最大支反力出现在66号墩b支座处为9 377 kN，最小支反力则出现在66号墩d支座处为952 kN，因此在设计中应特别注意支座型号的选用，以保证承载能力的需要。

4) 在各种最不利工况基本组合下，钢箱梁最大Mises应力达到232.8 MPa，发生在66号墩b支座处底板和支座加劲肋连接处，这是由于局部应力集中导致的。在设计中应对支座处构件进行适当加强，尤其需将底板加厚、横隔板加密，并单独设置支座加劲肋。

5) 局部轮压荷载作用下，横隔板具有足够的安全系数，不会发生屈曲。考虑钢筋混凝土板后的弹性屈曲特征值从50增大到229，表明钢筋混凝土桥面板大大增大了异形钢桥的刚度，使得荷载分配更为均匀，可有效地改善结构受力状况。

参考文献：

[1] 刘超凤. 城市高架桥异型曲线钢箱梁空间受力性能研究[D]. 长沙: 中南大学, 2012.LIU Chaofeng. The study of urban viaduct heterotypic curved steel box girder spatial mechanical behavior[D].Changsha: Central South University, 2012.

[2] ZHANG Yuanhai, LIN Lixia. Shear lag analysis of thin-walled box girders adopting additional deflection as generalized displacement[J]. Journal of Engineering Mechanics, 2014, 140(4): 1−8.

[3] TAI Yongpeng, LI Pu, FANG Yuming. Thermoelastic damping in torsion microresonators with coupling effect between torsion and bending[J]. Journal of Sound &Vibration, 2014, 333(333): 1509−1525.

[4] 何旭辉, 封周权, 陈政清, 等. 基于混合有限元法的钢箱拱相关稳定分析[J]. 铁道科学与工程学报, 2007,4(6): 7−11.HE Xuhui, FENG Zhouquan, CHEN Zhengqing, et al.Interactive stability analysis of steel box arch based on mixed finite element method[J]. Journal of Railway Science and Engineering, 2007, 4(6): 7−11.

[5] 卢彭真, 张俊平, 赵人达, 等. 箱梁单元与梁格法在异型桥梁分析中的应用[J]. 中山大学学报(自然科学版),2008, 47(2): 54−57.LU Pengzhen, ZHANG Junping, ZHAO Renda, et al.Application of a thin-walled box girder element and grillage method in the special-shaped bridge[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2008,47(2): 54−57.

[6] 戴公连, 李德建. 桥梁结构空间分析设计方法与应用[M]. 北京: 人民交通出版社, 2001.DAI Gonglian, LI Dejian. Spatial analysis and design method and its application for bridge structure[M]. China Communications Press, 2001.

[7] 刘振江, 陈钒. 梁格法及壳单元法在三跨连续箱梁桥计算中的比较[J]. 四川建筑, 2013, 33(3): 122−124.LIU Zhenjiang, CHEN Fan. Comparison between grid frame and shell element method in calculation of three-span continuous box girder bridge[J]. Sichuan Architecture, 2013, 33(3): 122−124.

[8] 董杰. 曲线连续钢箱梁梁单元与板单元模型计算分析[J]. 城市道桥与防洪, 2014(1): 59−60, 71.DONG Jie. FEM calculation and comparison of continuous curve steel box beam between beam element and plate element model[J]. Urban Roads Bridges &Flood Control, 2014(1): 59−60.

[9] 严定国, 王元汉. 异形连续箱梁桥的空间分析方法的研究[J]. 华东公路, 2005, 25(3): 93−95.YAN Dingguo, WANG Yuanhan. Research on spatial analysis method of special-shaped continuous box girder bridge[J]. East China Highway, 2005, 25(3): 93−95.

[10] Reissner E. On the problem of stress distribution in wide-flanged box-beams[J]. Journal of the Aeronautical Sciences (Institute of the Aeronautical Sciences), 2015,5(8): 295−299.

[11] 康崇杰, 戴公连, 粟淼, 等. 斜交薄壁连续钢箱梁桥设计与受力特性研究[J]. 铁道科学与工程学报, 2015,12(1): 119−126.KANG Chongjie, DAI Gonglian, SU Miao, et al. Design and mechanical analysis of skew steel box grid[J].Journal of Railway Science and Engineering, 2015, 12(1):119−126.

[12] 李海锋, 罗永峰. 横隔板对薄壁钢箱梁纵向正应力的影响[J]. 建筑结构学报, 2010(增1): 39−44.LI Haifeng, LUO Yongfeng. Influences of diaphragms of thin-walled box steel beams on longitudinal mormal stress[J]. Journal of Building Structures, 2010(Suppl 1):39−44.

[13] Chai H Yoo, Choi Byung H, Ford Elizabeth M. Stiffness requirements for longitudinally stiffened box-girder flanges[J]. Journal of Structural Engineering, 2001,127(6): 705−711.

[14] 李立峰, 邵旭东. 扁平钢箱梁闭口 U 形加劲板屈曲特性理论分析[J]. 公路交通科技, 2008, 25(3): 88−92.LI Lifeng, SHAO Xudong. Theoretical analysis plate stability property of U-rib stiffened flat steel box girder[J].Journal of Highway and Transportation Research and Development, 2008, 25(3): 88−92.

[15] Le, Canh V. A stabilized discrete shear gap finite element for adaptive limit analysis of Mindlin–Reissner plates[J].International Journal for Numerical Methods in Engineering, 2013, 96(4): 231−246.

[16] 李德建. 土木工程结构分析程序设计原理与应用[M].长沙: 中南大学出版社, 2014.LI Dejian. Civil engineering structure analysis programning principle and its application[M]. Changsha:Central South University Press, 2014.