以附加挠度为广义位移的双室箱梁剪力滞效应研究
2018-04-04张学西郭发蔚张玉元师彬杨娟
张学西,郭发蔚,张玉元,师彬,杨娟
(1. 中铁第一勘察设计院集团有限公司,陕西 西安 710043;2. 兰州交通大学 土木工程学院,甘肃 兰州 730070;3. 甘肃省陇南公路管理局,甘肃 陇南 746000)
薄壁箱梁因其有利的受力特性而被广泛应用于现代桥梁工程中。薄壁箱梁发生竖向挠曲变形时,由腹板传递给翼缘板的剪力流使翼缘板在远离腹板处的纵向位移滞后于靠近腹板处的纵向位移,从而使箱梁翼缘板不满足平截面假设,这就是剪力滞效应[1]。在薄壁箱梁的设计和计算时必须考虑剪力滞效应这已是众所周知的[1−3]。Reissner[4]针对不带悬臂板的双轴对称矩形截面箱梁,选取最大剪切转角差为广义位移,首次应用能量变分原理建立剪力滞效应分析理论。钱寅泉等[5-6]在Reissner的基础上,将矩形箱梁进一步拓展到带有悬臂板的斜腹板箱梁中,考虑截面翘曲正应力自平衡条件对各个翼板的纵向位移函数进一步修正,利用能量变分原理建立剪力滞效应分析理论,研究表明,考虑翘曲正应力自平衡条件获得的解析解计算精度得到进一步提高。近年来,国内外学者对剪力滞广义位移的选取有以下2种方式:方式一,采用最大剪切转角差为广义位移;方式二,采用附加挠度为广义位移;文献[7−9]中各个翼板采用同一最大剪切转角差为广义位移,此方式比较传统,自Reissner提出以来,至今应用较为广泛;文献[10−11]中从各个翼板在纵向翘曲时存在差异这一本质出发,考虑各个翼板选取不同的最大剪切转角差为广义位移,这对于研究剪力滞效应的精度有一定的提高,但是计算较为麻烦并且不具有明确的物理意义,不便于工程应用。文献[1−2,12−13]中采用附加挠度为广义位移,从应用和计算方面来讲,附加挠度具有明确的物理意义,便于工程人员理解和应用。此外,现有诸多文献在求解剪力滞效应时,将初等梁理论和剪力滞翘曲理论耦合在一起分析,这样不仅不能明确的反映剪力滞效应对初等梁理论的影响程度,而且不便于设计人员使用。本文将竖向对称荷载作用下的挠曲变形分解成剪力滞翘曲理论和初等梁理论2个独立的力学行为,选取附加挠度为广义位移,计算外力势能时考虑附加挠度的影响,同时引入参数对翘曲位移函数进一步修正,应用能量变分原理建立剪力滞效应分析理论。应用本文解研究简支箱梁作用集中荷载和均布荷载时,附加挠度及剪力滞效应对挠度提高幅度的影响规律。
1 控制微分方程及边界条件
1.1 微分方程的建立
箱梁在竖向对称荷载作用下的挠曲变形位移模式,可分解为初等梁理论下平截面假定的纵向位移和剪力滞翘曲模式下上下翼板剪切变形所产生的纵向位移。与传统分析剪力滞效应的方法不同,将初等梁理论和剪力滞翘曲理论解耦分析。针对剪力滞翘曲模式,假设坐标中心位于截面形心处,腹板服从平截面假定。箱梁截面简图如图1所示,箱梁在竖向任意荷载q(z)作用下的挠曲变形,选取附加挠度为剪力滞广义位移,则箱梁截面任意一点处的纵向位移u(x,y,z)为

图1中规定u(x,y,z)的方向为:当u与z方向一致取正,反之取负;w'(z)与f '(z)方向为:顺时针旋转为正,逆时针旋转为负。
其中:u0(y,z)为初等梁纵向位移;uω(x,y,z)为剪力滞翘曲位移;w(z)为初等梁挠度;ωζ(x,y)为剪力滞翘曲位移函数;f (z)为附加挠度。

图1 箱型截面简图Fig. 1 Box girder with cross section
图 1中,b1,b2,b3与 tu,tb,tu分别为顶板、底板、悬臂板的宽度和厚度;tw1和θ分别为斜腹板的厚度和倾角;tw2为中间直腹板厚度;hu为形心至顶板中面的距离;hb为形心至底板中面的距离;h为顶底板中面之间的距离,计算悬臂板时将x坐标原点放至翼缘板右侧端部。剪力滞翘曲位移函数取余弦函数,考虑截面翘曲正应力自平衡条件,引入修正系数d(0 各个翼板的应变能表达式: 顶板、底板应变能: 悬臂板应变能: 外力势能: 箱梁总势能: 将式(8)求一阶变分,并令0δΠ= 根据变分引理,由式(9)可得截面控制微分方程 式(13)中的待定系数由边界条件求解,f*为仅与q(z)分布有关的特解。 1) 附加挠度边界条件: 2) 初等梁挠度边界条件: 3) 变分要求的边界条件: 由弹性力学应力位移关系可得剪力滞翘曲正应力表达式 剪力滞翘曲正应力合成轴力为0 简支箱梁承受满跨均布荷载 q,结合简支边界条件解得附加挠度和初等梁挠度的解析解 简支箱梁承受跨中集中荷载P,将集中荷载P按照文献[14]介绍的方法换算成均布荷载并取其前4项 结合简支边界条件解得附加挠度和初等梁挠度的解析解 以文献[15]跨度 50 m 的简支单箱双室混凝土箱梁为例,截面尺寸、测点位置见图 2,材料E=3.1×104MPa,泊松比µ=1/6。满跨均布荷载q=2 kN/m;跨中集中荷载P=20 kN。 图2 截面尺寸及测点Fig. 2 Cross section size 利用本文求得的剪力滞效应纵向应力解分别求得集中荷载和均布荷载2种工况下跨中截面各个测点的纵向应力解,与文献[15]的有限元解对比分析,研究本文建立剪力滞效应分析理论的正确性。简支梁跨中截面测点纵向应力,如表1。 表1 简支梁跨中截面测点纵向应力Table 1 Longitudinal stress of cross section of simply supported beam kPa 由表1可以看出:集中荷载作用下,本文解与文献解的误差比在 1.73%~11.87%;均布荷载作用下,二者的误差比在0.10%~1.96%;二者误差比较小,验证了本文推导的剪力滞效应纵向应力解具有良好的计算精度。 采用图2所示的箱梁截面尺寸、跨度及荷载工况,沿跨度方向每隔5 m取一个测点,应用本文解析解及文献[16]初等梁挠度解,分析并绘制两种荷载工况下材料力学初等梁挠度、本文初等梁挠度、考虑剪力滞效应后的总挠度以及附加挠度随跨度的变化规律曲线,如图3~图5,表2示出了跨中截面挠度。 图3 集中荷载作用下挠度曲线Fig. 3 Deflection curves under the concentrated load 其中:w0为材料力学初等梁挠度;w为本文初等梁挠度;f为剪力滞效应引起的挠度;w+f为考虑剪力滞效应后的挠度(下同)。 图4 均布荷载作用下挠度曲线Fig. 4 Deflection curves under the uniform load 由图3和图4可以看出:2种荷载工况下,材力初等梁挠度和本文初等梁挠度吻合程度良好,证明了本文将剪力滞翘曲变形从一般的箱梁竖向挠曲变形中分离出来的假设是正确的,并且能够精确的反映剪力滞效应。剪力滞效应使得跨中区域挠度提高幅度较大,两侧支点附近的区域挠度提高幅度较小。由图5可以看出:2种荷载作用下,附加挠度由跨中向两侧支点递减,集中荷载对附加挠度的影响远大于均布荷载对附加挠度的影响。表2示出了2种荷载作用下的跨中截面挠度,均布荷载和集中荷载作用下,剪力滞效应对跨中挠度分别提高了3.17%和3.73%。 图5 附加挠度随跨度的变化曲线Fig. 5 Variation curves of the additional deflection with the span 表2 跨中截面挠度Table 2 Deflection of the cross section 1) 本文将箱梁的剪力滞效应与初等梁理论解耦分析,应用能量变分法建立了剪力滞效应分析理论。针对同一算例,对比本文初等梁挠度解和材料力学初等梁挠度解、跨中截面测点本文应力解和文献有限元解发现二者均吻合良好,证明本文将剪力滞纵向翘曲模式与初等梁竖向挠曲模式分离的假设是正确的。 2) 从剪力滞翘曲正应力自平衡这一条件出发,利用翘曲应力合成轴力为零将剪力滞翘曲位移函数进一步修正,通过算例验证并证实了此修正途径对于研究剪力滞效应具有良好计算精度。 3) 挠度分析得到以下几条规律:剪力滞效应对挠度提高幅度在跨中区域较明显,在两侧支点附近的区域较微小;附加挠度从跨中向两侧支点递减;对于本算例,剪力滞效应对均布荷载和集中荷载跨中挠度分别提高了3.17%和3.73%。 参考文献: [1] 张元海, 胡玉茹, 林丽霞. 基于翘曲位移模式的薄壁箱梁剪力滞效应分析[J]. 土木工程学报, 2015, 48(6): 44−45.ZHANG Yuanhai, HU Yuru, LIN Lixia. Analysis on shear lag effect of thin-walled box girders based on a modified warping displacement mode[J]. Journal of Civil Engineering, 2015, 48(6): 44−45. [2] ZHANG Yuanhai. Improved finite-segment method for analyzing shear lag effect in thin-walled box girders[J].Journal of Structural Engineering, 2012, 138(10): 1279−1284. [3] ZHOU Shijun. Finite beam element considering shear-lag effect in box girder[J]. Journal of Engineering Machinery,2010, 136(9): 1115−1122. [4] Reissner E. Analysis of shear lag in box beams by the principle of the minimum potential energy[J]. Quarterly of Applied Mathematics, 1946, 4(3): 268−278. [5] 钱寅泉, 倪元增. 单室箱桥的剪力滞分析[J]. 中国公路学报, 1989, 2(2): 28−37.QIAN Yinquan, NI Yuanzeng. Shear lag analysis of single room box girder[J]. Chinese Journal of Highway, 1989,2(2): 28−37. [6] 倪元增, 钱寅泉. 箱梁剪力滞计算的翘曲函数法[J].铁道学报, 1990, 12(2): 57−70.NI Yuanzeng, QIAN Yinquan. Warping function method for shear lag calculation of box girder[J]. Journal of Railway, 1990, 12(2): 57−70. [7] 谢旭, 黄剑源. 薄壁箱型梁剪力滞效应分析的刚度法[J]. 工程力学, 1995, 12(2): 95−101.XIE Xu, HUANG Jianyuan. Stiffness method for analysis of shear-lag effect on thin-walled boxed girder[J].Engineering Mechanics, 1995, 12(2): 95−101. [8] 冀伟, 吴焕庆, 刘世忠. 附加轴向位移对薄壁箱梁翼板应力的影响[J]. 公路交通科技, 2013, 30(9): 69−73.JI Wei, WU Huanqing, LIU Shizhong. Influence of additional axial displacement on flange stress of thinwalled box girder[J]. Highway Traffic Science and Technology, 2013, 30(9): 69−73. [9] 韦成龙, 曾庆元, 刘小燕. 薄壁箱梁剪力滞分析的多参数翘曲位移函数及其有限元法[J]. 铁道学报, 2000,22(5): 60−64.WEI Chenglong, ZENG Qingyuan, LIU Xiaoyan.Warping displacement function and finite element method for calculation of shear lag effect in box girder[J]. Journal of the China Railway Society, 2000, 22(5): 60−64. [10] 张玉元, 张慧, 李巍, 等. 基于选取不同剪力滞广义位移的薄壁箱梁剪力滞效应研究[J]. 铁道科学与工程学报, 2016, 13(6): 1083−1090.ZHANG Yuyuan, ZHANG Hui, LI Wei, et al. Analysis on shear-lag effect of box girders based on different shear–lag generalized displacement[J]. Journal of Railway Science and Engineering, 2016, 13(6): 1083−1090. [11] 罗旗帜. 基于能量原理的薄壁箱梁剪力滞理论与试验研究[D]. 长沙: 湖南大学, 2005: 24−27.LUO Qizhi. Theory and model test studies of the shear lag in thin-walled box girders based on energy principle[D]. Changsha: Hunan University, 2005: 24−27. [12] 杨绿峰, 周月娥. 基于挠度的剪力滞系数分析箱梁剪力滞效应[J]. 防灾减灾工程学报, 2013, 33(5): 494−496.YANG Lüfeng, ZHOU Yuee. Application of deflectionbased shear lag coefficient to analysis of shear lag effect of box-girders[J]. Journal of Disaster Prevention and Mitigation of Engineering, 2013, 33(5): 494−496. [13] 周茂定, 李丽园, 张元海. 薄壁箱梁的剪力滞翘曲位移函数研究[J]. 中国公路学报, 2015, 28(6): 67−73.ZHOU Maoding, LI Liyuan, ZHANG Yuanhai. Research on shear-lag displacement function of thin-walled boxed girders[J]. China Journal of Highway and Transportation,2015, 28 (6): 67−73. [14] 范立础. 桥梁工程(上册)[M]. 北京: 人民交通出版社,2012: 233−234.FAN Lichu. Bridge engineering (first volume)[M].Beijing: People Traffic Press, 2012: 233−234. [15] 牟兆祥. 基于能量变分原理的薄壁箱梁剪力滞效应解析法研究[D]. 长沙: 中南大学, 2014: 108−109.MOU Zhaoxiang. Analytical study on shear lag effect of twin-walled box girder based on energy-variational principle[D]. Changsha: Central South University, 2014:108−109. [16] 武建华, 郑辉中, 古滨. 材料力学[M]. 重庆: 重庆大学出版社, 2008: 388−390.WU Jianhua, ZHENG Huizhong, GU Bin. Mechanics of materials[M]. Chongqing: Chongqing University Press,2008: 388−390.
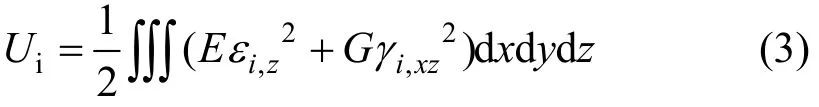
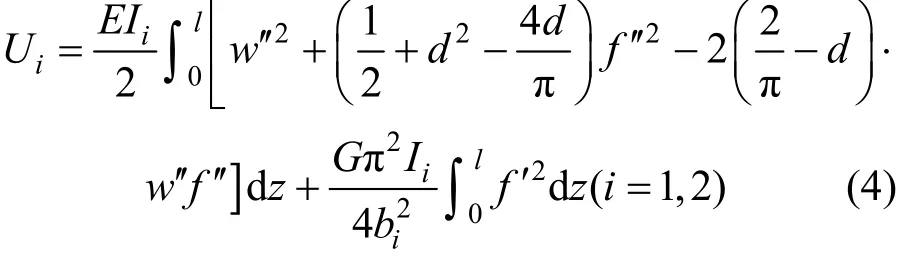






1.2 简支边界条件


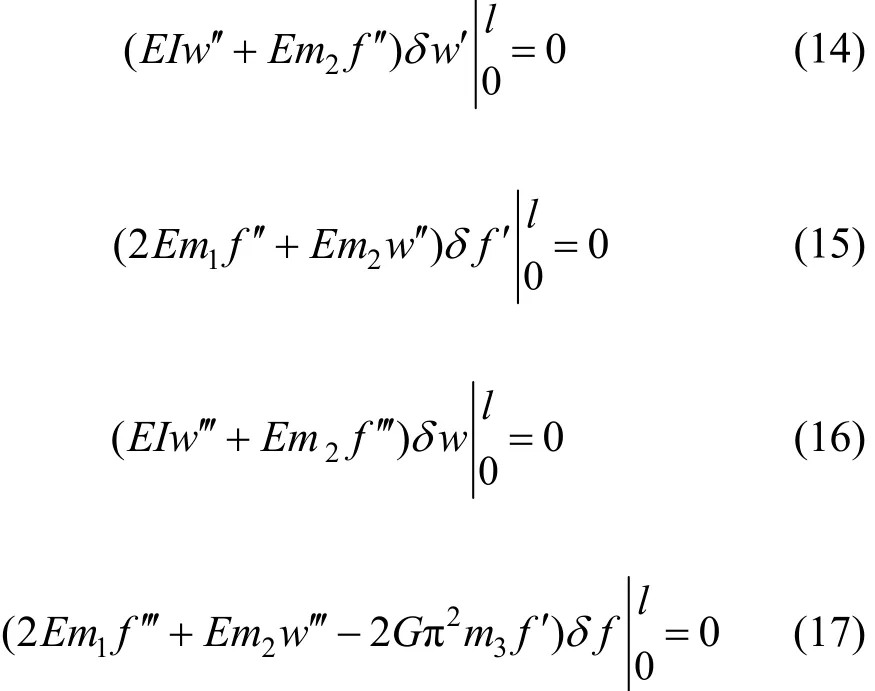
2 修正系数d的确定及挠度的求解
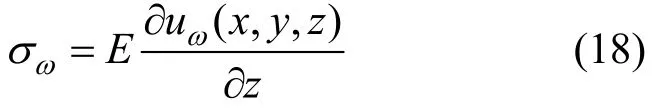




3 算例分析
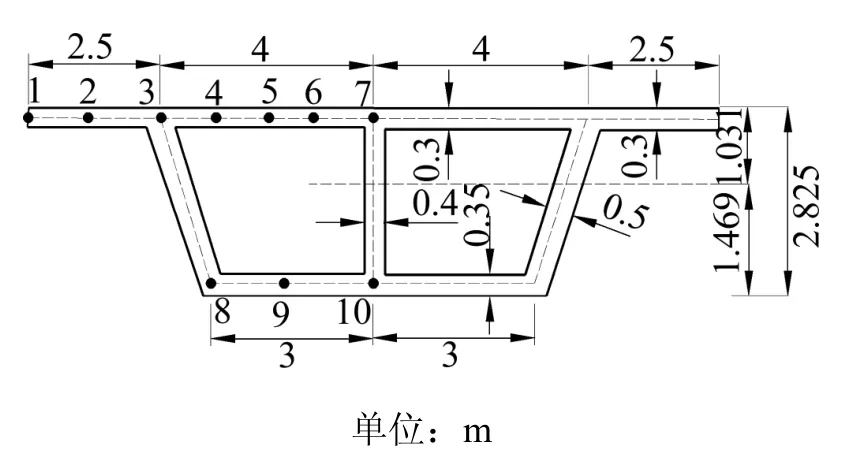
3.1 跨中截面正应力

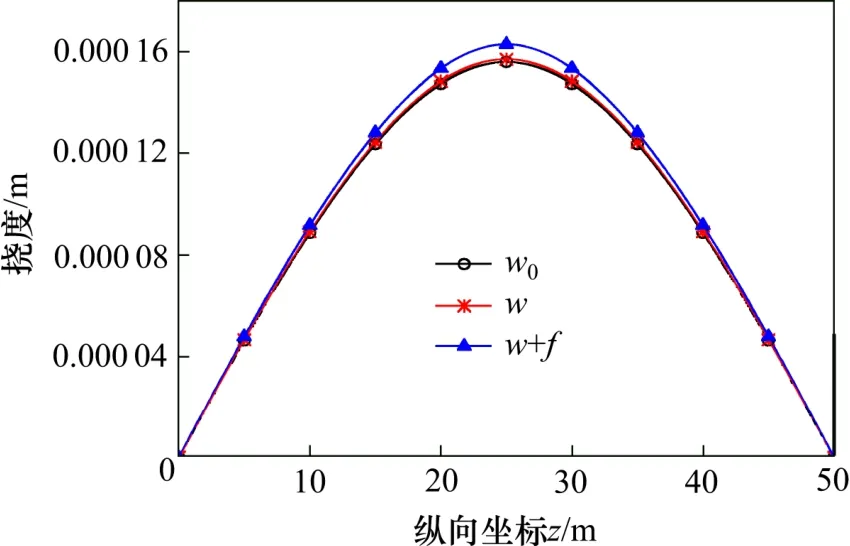
3.2 挠度分析



4 结论
