大跨度预应力混凝土连续刚构桥时域抖振分析

李　飞，刘多特

(1.中交基础设施养护集团有限公司，北京　100011；2.西南交通大学 土木工程学院，四川 成都　610031)

大气环境下的桥梁结构受到自然风的作用会发生振动。对风致振动现象的研究大多针对柔性体系的大跨度悬索桥或斜拉桥[1]，这类结构因其特有的施工方式、建设材料、约束条件等，一般允许主梁在体系转变前后存在一定的位移量。而内力重分配可通过施工监控[2]及成桥抗风性能的优化[3]予以有效的控制。但对于整体刚度偏大的预应力混凝土连续刚构桥，主梁断面比缆索承重桥梁更高、更钝，在风的作用下可能表现出更为复杂的空气动力效应[4]。与柔性体系桥梁的施工工艺不同，大跨连续刚构桥的预应力混凝土悬臂块一旦浇筑张拉完毕且达到材料龄期，后续可进行的整体线形调控空间非常有限[5]。这就要求各梁段在施工过程的体系转变中应具有足够的立模标高精度以适应内力的动态平衡，减小后期主梁合龙、桥面二期恒载施工的难度。因此，为满足成桥状态主梁的合理线形及内力优化分布，对该类体系桥梁的风致动力行为进行研究并为其监控提供必要的数据预测与反馈就非常重要，而专门针对此类桥型的研究较少。

结构风致振动现象主要包括驰振、颤振、涡振及抖振，其中驰振与颤振多发生于纤细及扁平柔性构件，涡振主要与断面构造形式有关，这3类振动问题均较少出现在刚度较大的连续梁或连续刚构桥上。抖振由自然风的脉动激励引起，并与风场背景成分和结构固有模态直接相关，是存在于任何大气条件下的环境振动，其随机往复变形也可能对结构的疲劳性能产生影响[6]。因此，本文采用数值模拟方法，结合计算流体动力学(Computational Fluid Dynamics，CFD)技术，以Scanlan准定常气动力[7]表达式为基础，对一座大跨度预应力混凝土连续刚构铁路桥的风致抖振现象进行研究，分析在施工最大双悬臂、最大单悬臂及成桥合龙3个关键状态下，主梁各节点的静风、抖振位移分布规律。

1　结构模型

预应力混凝土连续刚构桥桥跨布置如图1所示，其中hp为墩柱高。主梁采用变截面单箱单室梁，梁高由跨中至根部按抛物线渐变，顶板宽11.2 m。桥墩采用混凝土实心双薄壁墩，厚度均为2.5 m，宽度随墩高线性变化(见图2)。采用ANSYS Mechanical对主桥结构进行离散，其中，主梁桥墩等受弯构件均采用Beam 4单元模拟，二期恒载、转动惯量等均采用Mass 21单元模拟。

图1　桥跨布置(单位：m)

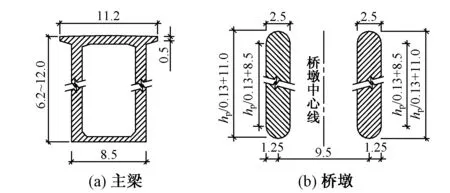
图2　主梁及桥墩断面尺寸(单位：m)

计算风致抖振效应工况共包括2个大悬臂及1个合龙状态。边界条件设置如下：最大双悬臂时(两侧梁端均未合龙前的最后1个体系)，仅约束左侧墩底全部自由度；最大单悬臂时(边跨梁端已浇筑合龙，中跨梁端即将合龙的最后1个体系)，增设与路基边坡相连梁端的竖向(y方向)、横桥向(z方向)的线位移约束及顺桥向(x方向)扭转与竖向的横弯限制；成桥合龙状态时，两侧墩底均被固结，进一步增加右侧边跨梁端y，z方向的线位移及x，y方向的角位移约束。对于最大双、单悬臂施工状态，本文均考虑边跨较大、墩高较高的左侧结构体系，模拟结构在不同状态下的基频与振型，见表1。可知，随着结构体系的进一步完善，自振频率单调增大。

表1　结构在不同状态下的基频与振型　Hz

2　时域抖振模拟

2.1　风场信息模拟

基于JTG/T D60-01—2004《公路桥梁抗风设计规范》[8]，结合桥址区地形地貌，近似将地表粗糙度取C类，地表粗糙度影响系数取0.22。该地区100年一遇10 min年平均最大风速V10=27.5 m/s。偏安全地考虑跨中桥面与最低通航水位距离d=69.58 m后，风速沿高度变化的修正系数K1c=0.785×(d/10)0.22=1.203，则桥面高程处设计基准风速U(d)=K1cV10≈33.08 m/s。在缺少脉动风场实测信息的情况下，根据JTG/T D60-01—2004可知z方向及y方向的脉动风速目标功率谱密度函数Sz(f),Sy(f)分别为

(1)

(2)

式中：f为风的脉动频率；ζ为折算频率，是关于f、离地高度y及其对应位置处平均风速U(y)的函数；u*为气流摩擦速度。

对于主梁而言，将其整体相关脉动风场简化为沿桥轴线分布的独立一维脉动风场后，可得到z方向及y方向的2个独立一维多变量随机信号。由于主梁共离散为119个单元，则沿x方向等间距模拟了120个风速点。时间步长取0.2 s，共模拟了 3 000 个时刻下总时长10 min的脉动风速片段。对于桥墩而言，由于各节点高程不同，考虑某一墩柱脉动风速的竖向相关性后，墩顶位置的平均风速近似由U(d)及0号块的高度确定。两桥墩(4肢)模拟点位总数为41，生成脉动风场包括x方向和z方向，模拟总时长为10 min，来流平均风速沿墩高按对数分布规律递增。采用基于三角级数叠加的谱解法(谐波合成法[9-10])模拟得到的主梁和桥墩脉动风速如图3所示，模拟边跨节点脉动风速功率谱如图4所示。

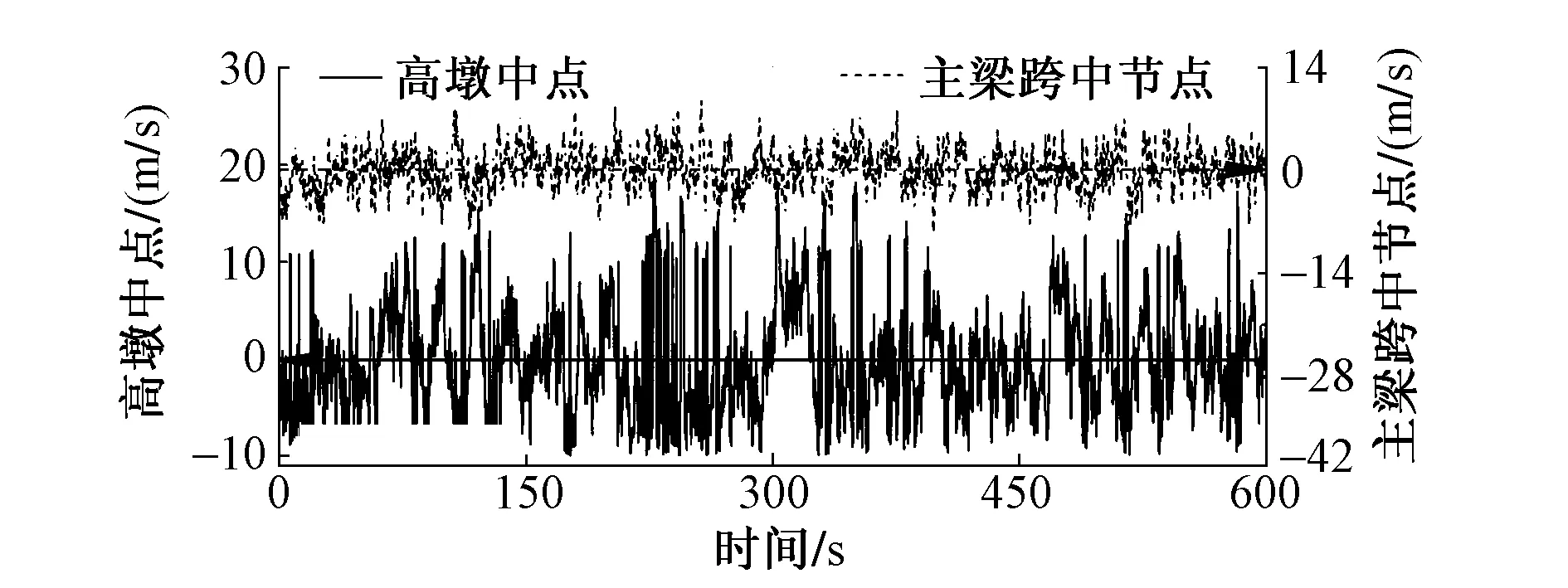
图3　模拟主梁和桥墩脉动风速

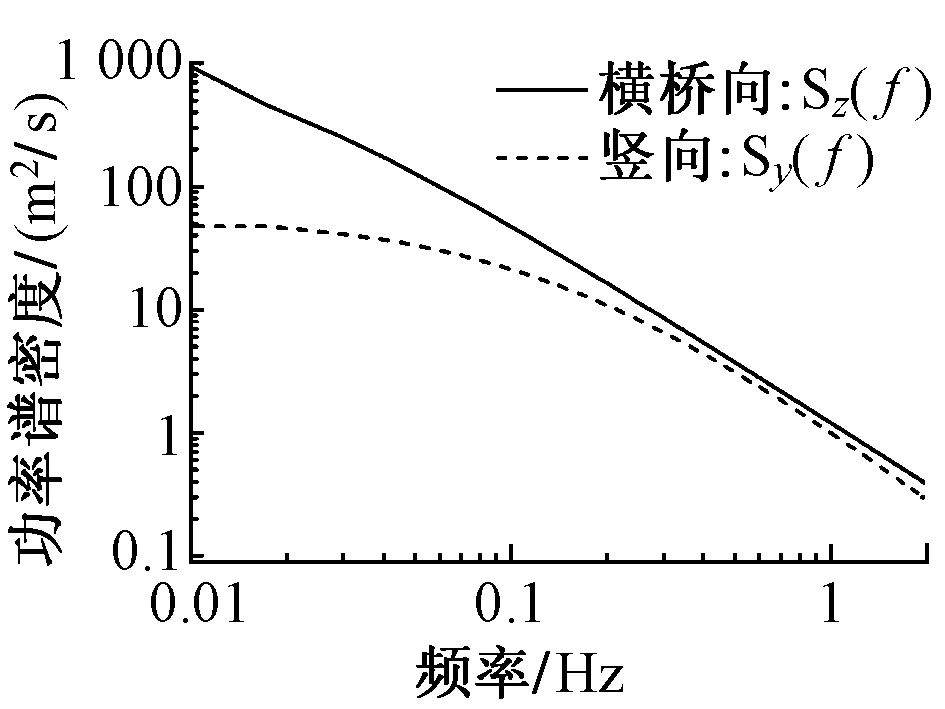
图4　模拟边跨节点脉动风速功率谱

2.2　静风气动力参数模拟

采用通用计算流体动力学软件FLUENT对图2中的主梁及桥墩断面进行静风气动力系数的求解。根据文献[11]中风洞实验的结论可知，对于变截面钝体绕流情况，当展向尺度远大于断面尺度时，其整体气动力效应可近似采用分段线性插值下的二维断面气动效应等效。因此，就主梁而言，根据桥跨对称性主要选取5种不同梁高断面进行网格划分。而桥墩由于线性变宽且尺寸沿墩高变化不显著，则选取墩顶及墩底断面进行计算。

静风气动力系数主要采用结构网格下的非定常模拟方式进行求解。对于各静风气动力系数斜率，本文采用非结构网格下的定常计算方式获得。为提高模拟精度，选用两方程的SSTk-ω湍流模型，并配合低雷诺数修正(Low-ReCorrections)方式对各断面进行求解。压力-速度耦合采用SIMPLEC算法，具体计算参数的设置及模型关键指标的验证可参见文献[4]。求解稳定后的计算跨中断面绕流速度分布见图5。

图5　计算跨中断面绕流速度分布(单位：m/s)

计算主梁静风气动力系数见图6，其余位置的系数可通过线性插值获得。可知，除0号块(x=98.9 m)断面外，计算来流平均风风攻角α0下的主梁断面阻力系数CD(α0)与升力系数CL(α0)总体随梁高增大而增大，而力矩系数CM(α0)随梁高变化不明显。对于墩梁固结位置，由于受桥墩影响，三维绕流效应复杂，采用二维方式得到的升力系数与力矩系数已不再服从真实气动行为。考虑墩顶对根部梁段的弹性约束较强，因此由上述位置对应系数CL(α0)，CM(α0)计算得到的0号块附近升力与力矩误差可忽略不计，其位移变形主要受气动阻力影响。

图6　计算主梁静风气动力系数(α0=0°)

对于尺寸变化不显著的桥墩断面，由墩顶与墩底断面所确定的在平均风风偏角β0=0°下墩柱平均阻力系数CD(β0)(z方向)为0.31，CL(β0)(x方向)与CM(β0)(y方向)则为0。

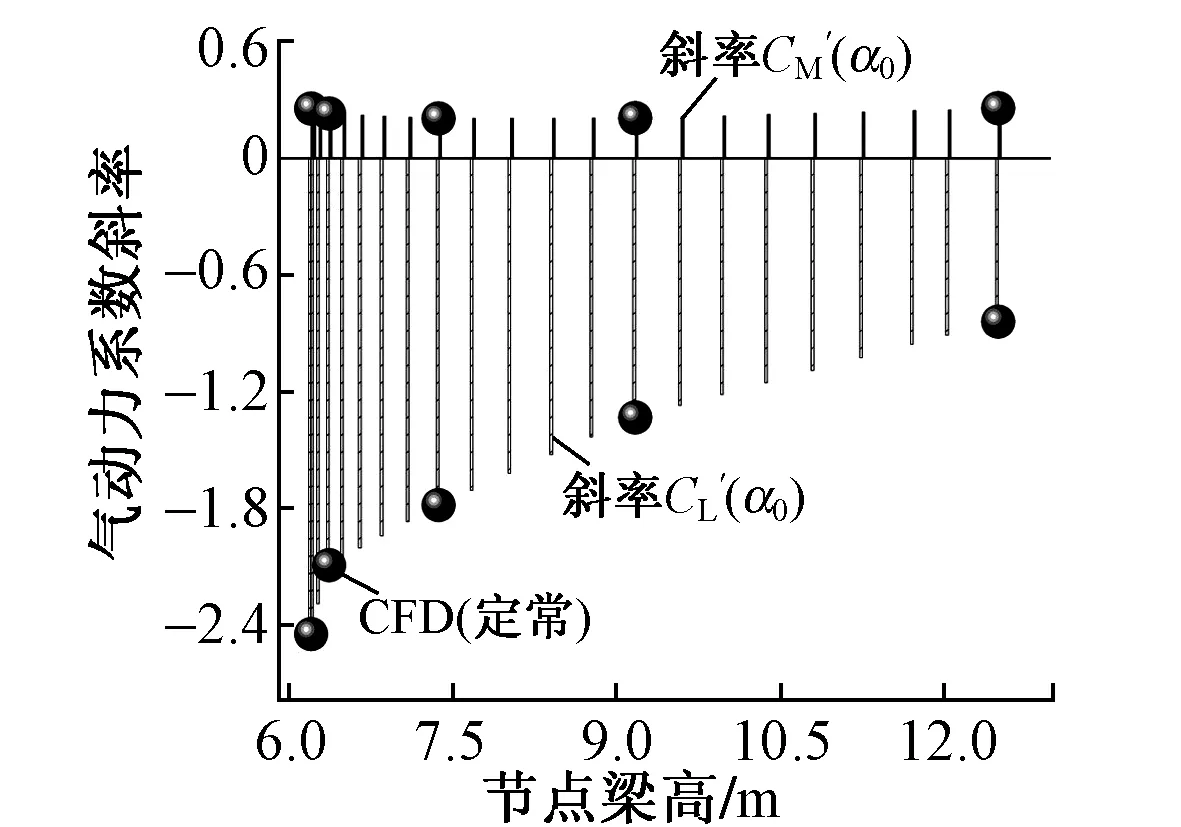
图7　计算主梁静风气动力系数斜率

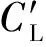
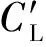
2.3　抖振及静风力计算

获取桥址区平均、脉动风场信息及主梁与桥墩断面的静风气动力系数、斜率后，可通过Scanlan准定常气动力表达式[7]对主梁及墩柱所受抖振力进行求解。考虑沿桥跨变化的主梁断面高度及各气动参数，作用于主梁上各方向的抖振力分别为

(3)

(4)

(5)

式中：Dbu，Lbu，Mbu分别为平均风(静风)风攻角α0=0°时，脉动风在来流及对应正交方向所形成的抖振阻力、抖振升力及抖振力矩。对于本文模拟的主梁而言，它们分别指向全局坐标z,y及x方向；对于桥墩而言，分别指向z，x及y方向。ρ为空气密度，取1.225 kg/m3；U为来流平均风速，可根据主梁及桥墩节点高度按风速廓线取值；B，D分别为主梁(桥塔)宽度与高度(厚度)；uz(x,t)与uy(x,t)分别为主梁展向x位置的水平(z方向)及竖向(y方向)的脉动风速，考虑到本桥为铁路桥，桥面宽度较窄，故忽略自激力的影响[12]。

计入静风效应后，静风阻力FD、升力FL及力矩FM[8]分别为

(6)

(7)

(8)

进行数值模拟时，首先求解不同结构在自重及静风力下的初始静变形，再对主梁及桥墩所有节点进行抖振力的加载。待瞬态分析完成后，对整个模型的节点位移时程结果进行提取。

3　计算结果及分析

3.1　施工悬臂状态

根据连续刚构桥的施工工艺可知，在最大双悬臂状态时梁端自由，结构最易发生绕桥墩扭转，出现主梁横摆的自振振型(参见表1)。此时，在来流作用下，风致振动现象相较于之前的各个悬臂浇筑阶段可能更为不利。

计算最大双悬臂主梁节点位移如图8所示，其中，Dis_,rms为主梁节点某一方向的线位移，相对位移为抖振位移与对应方向静风位移Dis_,avg的百分比。考虑连续刚构桥主梁断面整体抗弯扭刚度较大，且实际计算主梁节点静风位移及抖振转角位移非常小，后续不对其进行讨论。

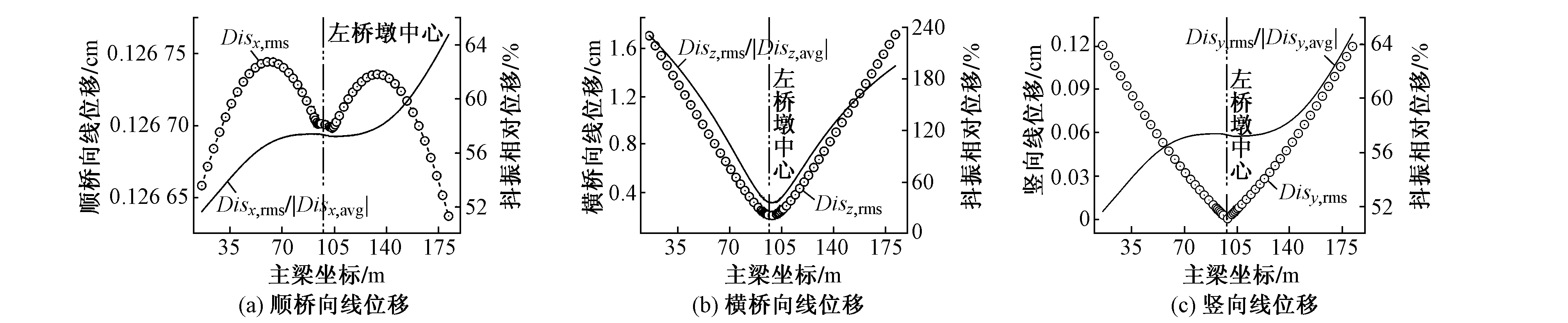
图8　计算最大双悬臂主梁节点位移(α0=0°)

由图8(a)可知，受桥墩风致作用力的影响，主梁各节点将发生沿x方向的均匀振动，但线位移总体较小，Disx,rms仅为1 mm左右，占静风位移的50%～60%左右；受桥墩限制，主梁节点横桥向抖振线位移Disz,rms最大值出现在两侧自由梁端，约为1.8 cm，且相对位移达到静风位移的240%，表明该方向结构的动力效应更为显著，内力由抖振力主导。由图8(b)可知，将横向线位移最大值的有效值换算至峰-峰值后，梁端往复横桥向振动幅值超过5 cm。由图8(c)可知，受双薄壁墩影响，主梁在y方向的振动RMS(Root Meam Square)分布仍表现为V形，Disy,rms总体小于1 mm，这主要与梁体竖向抗弯、抗剪刚度均较大有关。对于最大双悬臂状态下的连续刚构桥，受当前桥址区脉动风及主梁各方向刚度的影响，节点的最不利风致抖振位移响应主要发生在水平横桥向，且梁端最大横向位移超过竖向位移的10倍，施工监控时应予以关注。

主梁左侧边跨浇筑合龙时，计算最大单悬臂主梁横桥向线位移如图9所示。由于引入单侧梁端竖向及横向约束，该侧梁体的风致横向位移较双悬臂状态(参见图8(b))显著减小。同时，受结构协调变形影响，主梁各节点位移沿x方向单调增大，自由梁端节点抖振线位移最大值约为0.6 cm，占静风位移的40%。说明结构体系的转变所引起动力响应的改变程度大于静风响应的改变程度。相对于静风响应，结构形式的改变更容易引起抖振响应的较大改变。此时，内力由静风力主导。

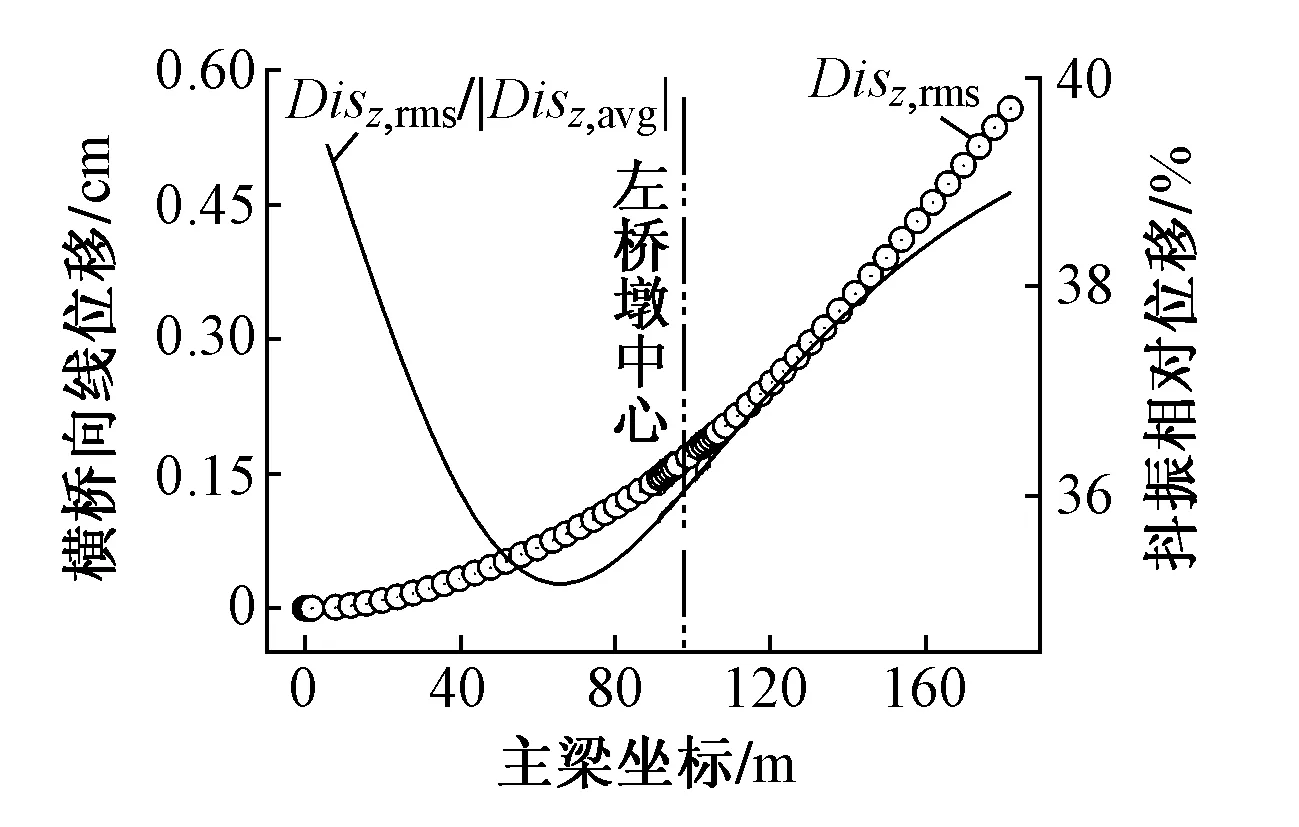
图9　计算最大单悬臂主梁横桥向线位移(α0=0°)

3.2　主梁合龙状态

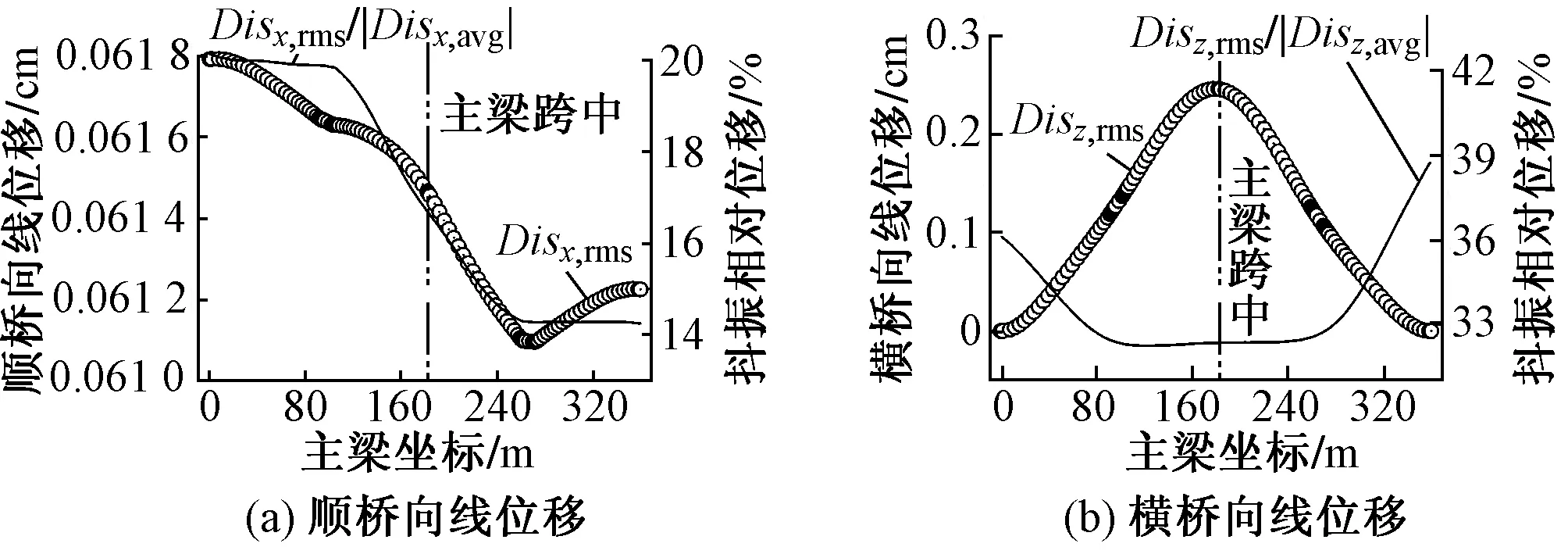
图10　计算合龙主梁节点位移(α0=0°)

计算合龙主梁节点位移如图10所示。由于两侧梁端均被约束，此时结构的整体刚度相对于之前2个施工悬臂状态均显著增大。由图10(a)可知，Disx,rms再度减小，仅为0.06 cm，约占最大双悬臂时的1/2。由图10(b)可知，受右边跨桥墩的影响，主桥部分形成完整框架体系，Disz,rms的最大值出现在跨中附近，约为0.25 cm，相较于前面2个悬臂状态进一步减小。由此可知，对于该种桥型，脉动风作用下的主梁抖振效应最不利工况为最大双悬臂状态时的梁端节点横向振动，但在结构合龙后，可忽略风致抖振效应的影响。

4　结论

对混凝土连续刚构桥施工大悬臂及合龙状态的风致抖振现象进行了时域数值计算，通过对比不同施工体系转变下主梁节点的位移响应，得到以下结论：

1)自然风引起的主梁节点位移响应并非总是以静风或抖振力作为主要控制外因，不同方向、不同施工体系下结构的动静力效应敏感程度随施工过程改变。

2)不同施工状态下，主梁节点的顺桥向及横桥向抖振线位移最大值随施工阶段的推进而单调减小。在最大双悬臂状态下，梁端节点横向往复振动位移超过5 cm，可能对监控产生干扰。

3)箱梁作为主要承重构件，因具有较强的竖向抗弯、抗剪及抗扭强度，故来流作用下连续刚构桥主梁节点的风致竖向及各方向转动位移均可忽略不计。

4)随着结构体系的逐渐完善，连续刚构桥风致动力效应逐渐减弱，内力由抖振力转变为静风力主导，这与结构基阶振动频率的提高有关。

[1]葛耀君.大跨度桥梁抗风的技术挑战与精细化研究[J].工程力学，2011，28(增2):11-23.

[2]赵晓晋，景强，贺拴海，等.港珠澳大桥青州航道桥主梁合龙施工技术[J].桥梁建设，2017，47(5):117-121.

[3]李永乐，侯光阳，向活跃，等.大跨度悬索桥钢箱主梁涡振性能优化风洞试验研究[J].空气动力学学报，2011，29(6):702-708.

[4]刘多特，李永乐，向活跃.错列双钝体断面气动绕流干扰效应的数值模拟[J].公路交通科技，2014，31(7):97-102.

[5]吴刚刚.高墩大跨曲线刚构箱梁桥挠度监控参数分析[J].公路，2016(9):180-183.

[6]韩艳，刘跃飞，刘志文，等.江顺大桥风致抖振响应及斜拉索疲劳损伤分析[J].长沙理工大学学报(自然科学版)，2016，13(3):50-57.

[7]SCANLAN R H，TOMKO J J.Airfoil and Bridges Deck Flutter Derivatives[J].Journal of the Engineering Mechanics Division，1971,97:1717-1733.

[8]中华人民共和国交通部.JTG/T D60-01—2004公路桥梁抗风设计规范[S].北京:人民交通出版社，2004.

[9]李永乐，周述华，强士中.大跨度斜拉桥三维脉动风场模拟[J].土木工程学报，2003，36(10):60-65.

[10]LI Y L,LIAO H L,QIANG S Z.Simplifying the Simulation of Stochastic Wind Velocity Field for Long Cable-stayed Bridge[J].Computer and Structures,2004,82(20/21):1591-1598.

[11]李永乐，刘多特，李少波，等.独柱式变截面倾斜桥塔气动特性风洞试验研究[J].实验流体力学，2013，27(5):38-43.

[12]张明金，李永乐，廖海黎.大跨度柔性斜拉-悬索体系风致静动力响应研究[J].工程力学，2014，31(2):151-157.