考虑悬臂板贡献的箱梁约束扭转效应研究

2018-04-04马俊军蔺鹏臻

铁道建筑 2018年3期

马俊军，蔺鹏臻

(1.兰州交通大学甘肃省道路桥梁与地下工程重点实验室，甘肃兰州　730070；2.兰州交通大学土木工程学院，甘肃兰州　730070)

箱形截面因其独特的结构性能在国内外大跨度桥梁建设中一直被广泛采用。为了满足这种大跨度的要求以及高强轻质材料的选用和预应力技术的快速发展，箱梁的截面变得更薄更宽。但是，薄壁宽箱梁在偏心荷载作用下除了发生纵向的弯曲作用外，还会发生很大的扭转和畸变。目前，很多学者在箱梁扭转分析方面进行了大量研究。文献[1]利用块体有限元方法对箱梁约束扭转效应进行了分析。文献[2-5]基于传统薄壁杆件理论，建立了考虑箱梁剪切变形和翘曲应力影响的梁单元，并对箱梁的约束扭转效应进行了分析。文献[6-7]在考虑自由扭转刚度影响的翘曲理论的基础上，提出了一种新的数值分析方法——单肢解析化分析方法。文献[8-9]在薄壁杆件理论的基础上，通过考虑箱梁约束扭转时二次剪切变形对翘曲位移的影响，分析了曲线箱梁的剪滞效应和挠曲扭转效应。文献[10]研究发现，悬臂翼缘板对箱梁约束扭转存在很大的影响，在箱梁发生约束扭转时，翼缘板导致箱梁约束扭转正应力发生应力重分布。文献[11]进行了长悬臂板箱梁畸变效应的试验研究，结果表明大悬臂箱梁比普通箱梁的空间效应更显著，在结构设计和分析时应予以重视。虽然上述文献从不同的角度利用不同的方法分析了箱梁的约束扭转效应，但大多数文献在计算时仅考虑了箱梁中闭口截面部分对箱梁约束扭转的贡献，很少有文献考虑箱梁的翼缘板部分对箱梁约束扭转的影响。

基于以上论述，在采用箱梁除翼缘板外闭口截面部分计算截面几何特性的基础上，本文通过求解截面极惯性矩时考虑箱梁翼缘板部分对截面极惯性矩的影响，对箱梁约束扭转公式进行修正。利用修正前后的计算公式分别计算简支箱梁在约束扭转时截面的翘曲应力及内力，再与有限元计算结果进行对比，并研究结构参数对箱梁约束扭转效应的影响和变化规律。

1　约束扭转分析理论

1.1　基本假定

为了便于分析，假设箱梁约束扭转满足自由扭转时的3个基本假定[12-13]：①横截面周边不变形；②横截面上法向应力和剪应力沿壁厚均匀分布；③横截面上位移的分布规律和自由扭转时的一样。

1.2　翘曲正应力及内力

根据文献[13]可知，箱梁在发生扭转时截面的变形如图1所示，截面产生的翘曲正应力为

(1)

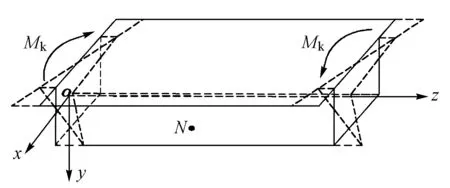
图1　截面变形

为了便于描述箱梁在约束扭转时内力的变化规律，引入约束扭转双力矩，则式(1)可描述为

(2)

1.3　翘曲剪应力及内力

根据基本假定②，用截面翘曲剪力流qW来代替截面翘曲剪应力τW。根据图1中N点微元体纵向平衡条件可得[15]

(3)

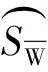
根据文献[13]可以得到截面上自由扭转剪应力为

(4)

1.4　约束扭转微分方程及求解方法

根据扭转时剪应变方程和切线位移方程以及翘曲位移的连续性条件(沿截面周边积分一周，积分起始点纵向位移等于积分终止点纵向位移)，得到关于扭转角φ的约束扭转微分方程[13]为

EIWφ″″-μGIdφ″=μm-EIWm″/(GId)

(5)

式中：μ为截面约束系数，μ=1-Id/Iρ，其中，Iρ为采用闭口截面计算的极惯性矩;G为材料的剪切模量；m为截面的外扭矩。

本文采用2种方式计算Iρ：

1)不考虑悬臂板贡献，极惯性矩Iρ为箱梁除翼缘板外的闭口截面对扭转中心的积分，计算公式为

Iρ=∮ρ2tds

(6)

式中，ρ为截面积分点到截面扭转中心的距离。

(7)

实际工程结构中，桥跨结构往往以承受竖向集中荷载或均布荷载为主，此时截面的外扭矩的二阶导数(m″)为0，则式(5)可进一步简化为

EIWφ″″-μGIdφ″=μm

(8)

箱梁所受外加扭矩如图2所示。

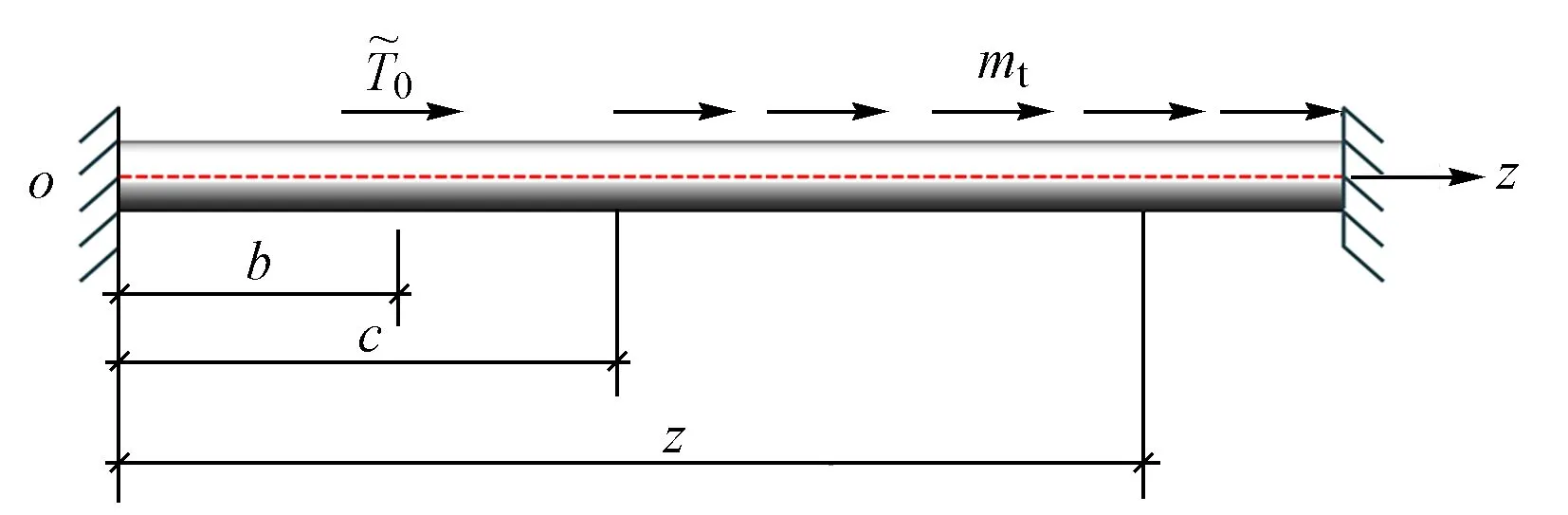
图2　箱梁所受外加扭矩

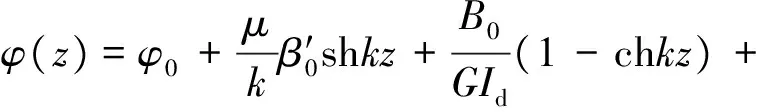
(9)

(10)

(11)

(12)

根据式(9)—式(12)以及箱梁约束扭转的边界条件，可求解任意荷载作用下箱梁的约束扭转效应。

2　约束扭转翘曲应力和截面内力分析

图3　箱梁截面(单位：dm)

2.1　翘曲应力分析

针对上述混凝土简支箱梁，本文分别按照第Ⅰ类分析方法和第Ⅱ类分析方法得到了在均布扭转力矩作用和集中扭转力矩作用下，跨中截面和梁端截面控制点的翘曲应力，分别见表1和表2。同时，为了便于比较，本文还采用ANSYS软件中的Shell 63单元分别建立了2种工况下的混凝土箱梁有限元模型。每个模型共计采用 5 246 个结点、5 160 个单元，并将有限元计算结果分别列于表1和表2中。

表1　均布扭转力矩作用下翘曲应力　kPa

表2　集中扭转力矩作用下翘曲应力　kPa

由表1可知，按第Ⅰ类和第Ⅱ类方法得到的计算值与有限元解吻合良好。在均布扭转力矩作用下，箱梁跨中截面翼缘板端部翘曲正应力和顶板中心处翘曲剪应力最大。另外，按第Ⅱ类方法得到的翘曲应力比按照第Ⅰ类方法的结果整体上大。虽然按2种方法计算的翘曲正应力相差较小(差值不到1%)，但翘曲剪应力相差较大，跨中截面顶板中心处按第Ⅱ类方法得到的翘曲剪应力是第Ⅰ类方法的128%。

由表2可知，按第Ⅰ类和第Ⅱ类方法得到的计算值与有限元解比较吻合，说明本文的方法能够准确分析箱梁的约束扭转效应。与均布扭转力矩作用下翘曲应力的变化相比，在集中扭转力矩作用下应力变化更加明显，按第Ⅱ类方法得到的跨中截面悬臂板端部翘曲正应力是第Ⅰ类方法的127.68%；按第Ⅱ类方法得到的梁端截面顶板中心处翘曲剪应力是第Ⅰ类方法的163.7%。

2.2　截面内力分析

在上述分析的基础上，按照2种分析方法进一步得到在均布扭转力矩和集中扭转力矩作用下各个截面约束扭转翘曲内力的变化情况，结果分别如图4、图5所示。其中，l为跨度。

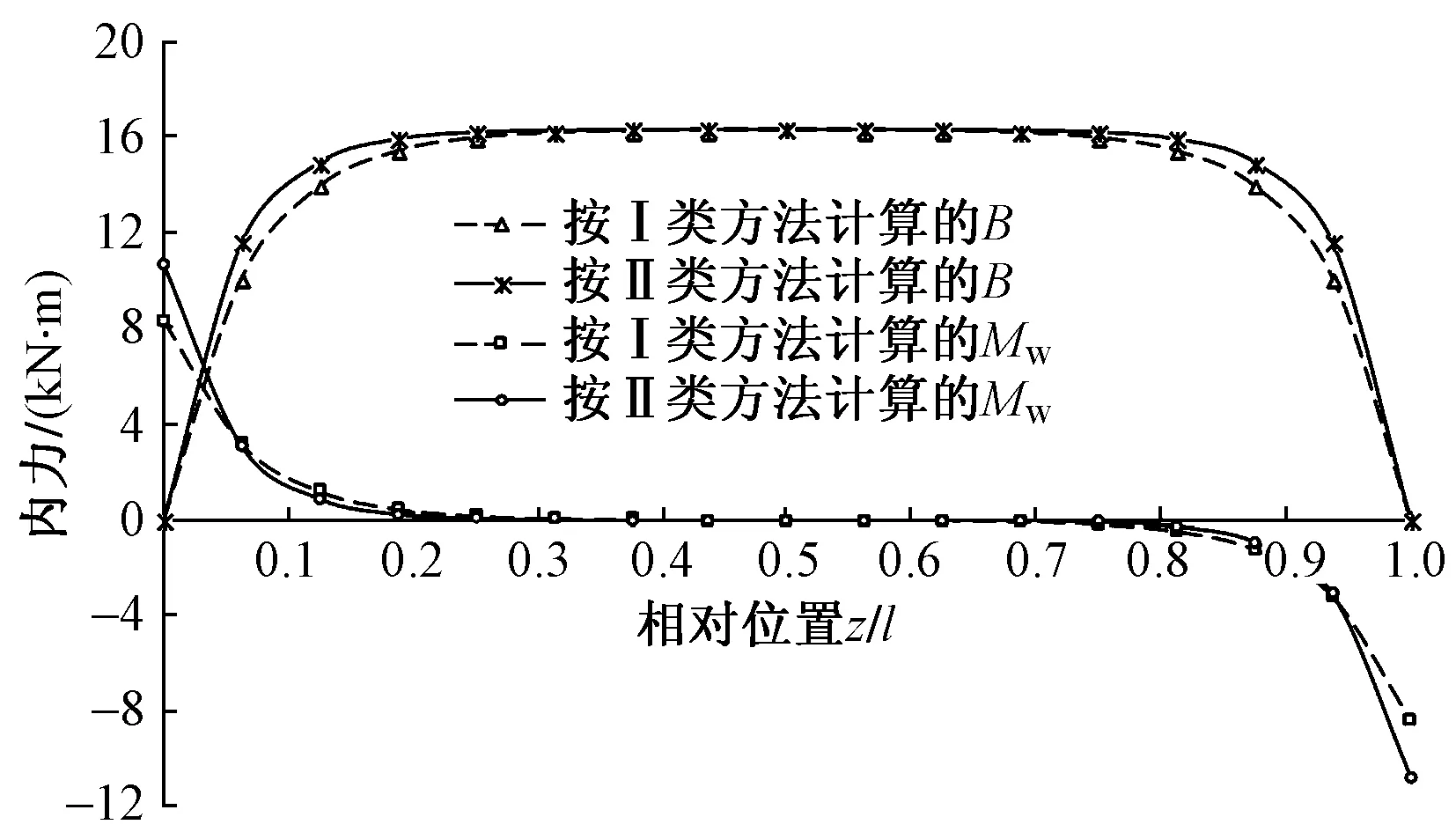
图4　均布扭转力矩作用下的内力曲线

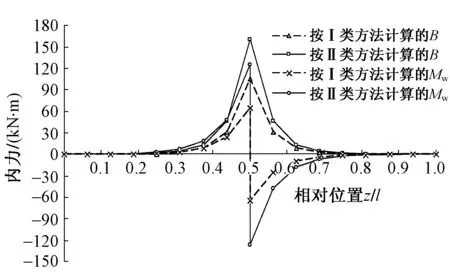
图5　集中扭转力矩作用下的内力曲线

由图4可知，随着截面与梁端距离的减小，截面约束扭转双力矩逐渐减小，而截面二次扭矩逐渐增大，说明截面翘曲正应力逐渐减小、翘曲剪应力逐渐增大。距跨中0.2l范围内，按2种方法计算的箱梁约束扭转内力很接近，这段范围内只产生翘曲正应力，而翘曲剪应力几乎为0。在距离梁端0.3l范围内，按第Ⅱ类方法计算的内力值比按第Ⅰ类方法计算的偏大。

由图5可知，在集中扭转力矩作用下，按第Ⅱ类方法计算的约束扭转内力值比按第Ⅰ类方法计算的大。在集中扭转力矩作用处的截面，其约束扭转双力矩和二次扭矩都非常大，但衰减很快，这将使此处截面产生很大的翘曲应力，而远离该截面的约束扭转双力矩和二次扭矩几乎为0，几乎不会产生翘曲应力。

3　结构参数对约束扭转内力的影响

3.1　高跨比

高跨比(h/l)是箱梁重要的设计参数之一。在跨径为30 m的简支箱梁上作用集中扭转力矩705 kN·m，通过改变桥梁跨度来实现高跨比的变化。高跨比对约束扭转效应的影响如图6所示。

图6　高跨比对约束扭转效应的影响

由图6可知，对跨中截面而言，截面约束扭转双力矩和二次扭矩最大，且不随高跨比的变化而变化。对除跨中截面外的任意一个截面而言，高跨比越小，截面约束扭转双力矩和二次扭矩越小，受约束扭转影响的截面的范围越少，说明箱梁受约束扭转效应的影响越小。

3.2　高宽比

截面的高宽比(h/b)对箱梁的约束扭转有很大的影响。在跨径为20 m的箱形简支梁跨中作用集中扭转力矩705 kN·m，通过改变截面高度来实现截面高宽比的变化。高宽比对约束扭转效应的影响如图7所示。

图7　高宽比对约束扭转效应的影响

由图7可知，对于箱梁任意截面，尤其是跨中截面，在集中扭转力矩的作用下，截面约束扭转双力矩和二次扭矩均随高宽比的增加而减小，但箱梁受约束扭转影响的范围没有发生变化。

3.3　宽厚比

截面的宽厚比(b/δ)是影响箱梁约束扭转的另一个重要因素。在跨径为20 m的箱形简支梁跨中作用集中扭转力矩705 kN·m，其顶板厚度分别为0.2，0.3，0.4 m，底板厚度变化规律与顶板相同。保持截面腹板厚度和宽度不变，通过改变截面的顶板和底板厚度来研究截面宽厚比对约束扭转内力的影响。宽厚比对约束扭转效应的影响如图8所示。