基于预估-反馈联合处理的射频噪声干扰抑制算法

王国宏，孙殿星，白杰，张翔宇

海军航空大学, 信息融合研究所,烟台 264001

现代雷达所面临的电磁环境日益恶劣，针对雷达的电磁干扰技术迅速发展，噪声压制干扰作为一种常用的干扰类型，通过在时域和频域对目标回波信号形成全覆盖达到其压制干扰效果，其中射频噪声干扰相比于噪声调制类干扰，其信号熵值最大且遮盖性较好[1]，从而增大了雷达对抗的难度，同时，线性调频(Linear Frequency Modulation, LFM)信号具有较大的时宽带宽积，能够同时满足作用距离和距离分辨率的要求，从而被广泛应用于现代雷达系统中,所以适用于脉冲压缩雷达的射频噪声干扰抑制技术对雷达的实战和发展具有实际性的推动作用。

目前，国内外学者在噪声干扰抑制方面做了大量研究，文献[2-3]通过不同算法实现目标回波信号与干扰信号的分离，从而达到干扰抑制的目的；文献[4-6]分别提出了在干扰背景下直接进行目标检测的算法；文献[7-8] 利用LFM信号在分数阶傅里叶变换(FRFT)域的处理增益，通过构建滤波器实现干扰抑制。上述文献基于信号层的处理，从不同角度入手，较好的实现了对噪声压制干扰的抑制，但是上述文献均未建立合理的干扰抑制检验量，而算法参数又很难在没有任何先验信息的情况下达到最优，从而导致算法实时性以及在不同环境下的“应变能力”较差。

文献[9]通过点迹关联、数据压缩以及数据跟踪等技术，解决了压制干扰下雷达目标检测概率低的问题；文献[10] 通过建立量测模型及序贯滤波跟踪，提升了组网雷达的目标检测与跟踪能力；文献[11] 提出了点目标概率多假设跟踪(DC-PPMHT)算法，降低了航迹丢失率；文献[12] 依据干扰强度选择基于粒子滤波的检测前跟踪(PF-TBD)或门限自适应的多假设跟踪，提高了远距离支援干扰下的目标跟踪能力。上述文献利用目标点迹和噪声点迹的不同特征，通过数据层处理达到了干扰抑制的目的，但由于缺乏目标运动的先验信息，为减小漏检概率，会在较大的速度、加速度以及运动方向范围内对目标点迹进行检测，从而导致当压制干扰较强，噪声点迹较密集时，过多的噪声点迹满足判决条件，造成真实目标的检测以及跟踪困难。

针对上述文献所出现的问题，本文提出了一种基于预估-反馈联合处理的射频噪声干扰抑制技术，通过将信号层的信号估计算法和数据层的航迹检测算法相结合，并对反馈调节环节进行构建，有效实现了射频噪声干扰的抑制。

1 问题描述

假设在一段观测时间内目标的运动速度不变，在强射频噪声干扰环境下脉压警戒雷达所接收到的回波信号x(t)为

JRF(t)+n(t)

(1)

式中：si(t)为第i个目标的回波信号；Ai、fi和φi(i=0,1,…,k-1)分别为第i个目标回波的幅度、载频和相位；μ为LFM信号的调制斜率；n(t)为背景噪声，包括接收机热噪声、电磁环境噪声、杂波噪声等，为高斯白噪声；JRF(t)为射频噪声干扰，由带限高斯白噪声放大产生，其时域表达式为

JRF(t)=Uj(t)cos[ωjt+φ(t)]

(2)

式中：Uj(t)为包络函数，服从瑞利分布；φ(t)为相位函数；ωj为中频窄带噪声的中心频率，且ωj远大于JRF(t)的谱宽。

由式(1)可以看出，强射频噪声干扰环境下的干扰抑制技术需要解决以下几个问题：

1)射频噪声干扰在时域和频域对LFM信号形成全覆盖，如何在强噪声干扰环境下利用信号特性差异实现干扰能量消除，是信号层处理需要解决的难题。

2)信号层处理之后，噪声点迹与目标点迹并存，如何对所有可能形成的航迹进行检测以减小漏检概率，是数据层处理需要解决的难题。

3)信号层的干扰消除效果依赖于算法参数的选择，如何利用数据层对航迹的实时估计，对信号层算法参数进行调整，是联合处理需要解决的难题。

2 射频噪声干扰抑制技术

综合考虑以上问题，本文拟从以下3个方面进行强射频噪声干扰的抑制：①信号层窄带滤波，以解决干扰消除问题；②数据层逻辑判决，以解决航迹生成问题；③反馈调节，以解决参数调节问题。本文总体思路如图1所示。

2.1 基于信号估计的窄带滤波干扰消除

首先对回波信号进行盲源分离预处理，以解决目标回波之间的交叉干扰[13]问题，然后利用LFM信号在FRFT域不同阶次的不同特性，通过对LFM信号能量聚集点的坐标估计，构建窄带滤波器进行信号层干扰消除。基于坐标估计的信号层窄带滤波干扰消除原理如图2所示。

图中：B为LFM信号带宽；T为LFM信号时长。在FRFT某一变换阶次，如图2中轴所示，LFM信号表示为复正弦信号，且正弦信号载频与LFM信号的载频存在确定关系，因此利用子空间正交方法[14]可以完成LFM信号的检测和参数估计，而在FRFT域的正交变换阶次，如图2中轴所示，LFM信号表现为冲激函数，此时能够根据参数估计结果对LFM信号的能量聚集点坐标进行估计，并基此构建窄带滤波器，完成滤波处理。

2.1.1 Fast ICA算法盲源分离预处理

由式(1)可以看出，在实际干扰环境下，雷达所接收的信号是由不同目标回波和干扰信号组成的混合信号，由于不同目标回波信号之间相互独立，且满足非高斯分布的要求，所以本文首先采用独立成分分析(ICA)算法对多分量LFM信号进行分离，同时考虑到基于最大负熵理论的Fast ICA算法收敛速度为3阶，较ICA算法的线性收敛速度更快，算法实时性更强，所以本文最终采用Fast ICA算法对回波信号进行处理。

假设战场环境中目标个数n不大于接收系统的通道数m，采用多通道宽带接收体制对多分量LFM信号进行接收，复数信号矩阵形式表示为

X=AS

(3)

式中：X=[x1x2…xm]T为m个观测复数信号矢量；S=[s1s2…sn]T为n个独立复数信号矢量包括n-1路LFM信号和1路噪声干扰信号；A=[ωij]为m×n维复数混合矩阵，并且A列满秩。Fast ICA算法主要包括中心化、白化和独立分量提取3个步骤，其处理流程如图3所示。

(4)

(5)

最后提取独立分量，采用峭度来衡量分离信号的非高斯性，由于目标回波信号满足非高斯分布，所以如果存在矩阵B，使得Y=BHZ的各个分量的峭度值离零值最远，则认为Y是对源信号S的估计。对于矩阵B的具体求解过程可参考文献[15]，本文在此不再赘述。

通过对回波信号进行Fast ICA预处理，使得不同分量目标回波信号相分离，既减小了强目标回波信号对弱目标回波信号检测的影响，同时对信号信干比也有所改善。

2.1.2 LFM信号检测与参数估计

在强噪声干扰环境下，目标回波(LFM)信号在FRFT域的能量聚集点被干扰信号所淹没，从而导致传统的基于峰值搜索的聚集点坐标估计算法不再适用，但是滤波器始末位置的确定需要以LFM信号的能量聚集点坐标为参考，为此，本文利用子空间正交方法更优的抗干扰能力，首先进行LFM信号的检测和参数估计[16-17]，然后再根据参数估计结果进行聚集点坐标的估计。

经过Fast ICA预处理后，除噪声分量之外各分量信号统一表示为

r(t)=s(t)+N(t)=exp{-j[(ω0+ωd)t+

μt2/2+φ]}+N(t)

(6)

式中：ω0为发射信号载频；ωd为目标多普勒频移；N(t)为噪声干扰信号，满足高斯分布。

当FRFT变换角度α1满足α1=-arctanμ时，LFM信号的FRFT变换为[18]

Aexp(-juωcosα1)

(7)

式中：w为LFM信号的载频；

exp[-j(ω2sinα1cosα1-φ)/2]。

由式(7)可以看出Sp(u)为一个严格的复正弦信号，定义此时的变换阶次为LFM信号的平行变换阶次。由于FRFT是线性变换，式(6)的FRFT变换为

Rp(u)=A′exp(-jωnu)+Np(u)

(8)

式中：ωn=(ω0+ωd)cosα1为正弦信号角频率；A′为复值常量；Np(u)=FRFTp[N(t)]，满足高斯分布。

对式(8)进行抽样，并用矩阵形式表示：

R(k)=A′exp(jkωn)γ+N(k)

(9)

式中：γ=[1ejωn…ejmωn]T；N(k)=[Np(k)Np(k+1)…Np(k+m)]T。

向量R(k)的协方差矩阵为

(10)

由于矩阵rank(γγH)=1，根据文献[19]的结论容易证明：

(11)

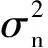
由于多普勒频移的存在，当分量信号中存在目标回波信号时，信号频率满足：

(12)

式中：wdmax为多普勒频移最大值。

通过子空间正交方法最终得到LFM信号的载频为

(13)

以上完成了LFM信号的检测和估计，当有LFM信号存在时，根据以上所得到的载频估计，可以对LFM信号在FRFT域的能量聚集点坐标进行估计，进而构建窄带滤波器，完成窄带滤波过程。

2.1.3 LFM信号窄带滤波

由于LFM信号的线性时频特性使得LFM信号在FRFT域具备能量高度聚集的特征，而射频噪声干扰以及过程噪声则不具备此特征，据此建立窄带滤波器，使得LFM信号的能量包含在滤波器宽度范围之内，而干扰以及噪声的能量在滤波器宽度范围之外，以此在完整保留LFM信号能量的前提下滤除大部分干扰和噪声的能量[20]。

当变换角度α2与LFM信号的调频率正交时，即α2=arctan(-1/2πμ)，LFM信号的FRFT变换可表示为

|Sp(u)|=|A(t)Aα2σ(ω-ucosα2)|

(14)

由式(14)可以看出，当变换角度α2与LFM信号的调频率正交时，LFM信号在u域表现为冲激函数，具有明显的能量聚集效果，并称此时的变换阶次为FRFT域LFM信号的正交变换阶次。根据LFM信号的能量聚集特性构建窄带滤波器，使滤波器输出在完整保留LFM信号能量的同时，滤除大部分噪声干扰能量。

为了对量纲进行归一化处理，引入尺度因子S=T/fs，定义新的尺度化坐标为

(15)

式中：T为观测时间；fs为采样频率。新的坐标实现了无量纲化。

根据式(13)，LFM信号在(p,u)二维平面上的能量聚集点坐标(p0,u0)估计为

(16)

L=2ρsin(p0π/2)S/(2πcosα1)+2/B

(17)

式中：ρ为目标多普勒频率的估计误差标准差。由式(17)可以看出，载频的估计精度直接决定着滤波器宽度L的取值。

2.2 基于逻辑判决的数据层航迹检测

在恒虚警检测形成点迹之后，利用目标的运动特性在数据层对点迹进行处理：由于受机动性能的影响，目标点迹满足一定的分布规律，而噪声点迹则呈现出无序性的特点，运用M/N逻辑法对所有可能生成的航迹进行检测，并根据信号层对目标运动状态的估计，利用径向速度方向判决算法，对不满足要求的噪声航迹进行剔除。

2.2.1 基于M/N逻辑法的航迹检测

M/N逻辑法是以多重假设的方式通过预测和相关波门来确认可能存在的航迹，当N个扫描周期中有M个观测点落入相关波门中时判断航迹起始成功。

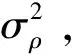
(18)

式中:c为光速。

量测协方差矩阵R为[22]

(19)

式中：

(20)

运用M/N逻辑法对目标进行检测。其具体工作方式如图4所示。

1)在xoy坐标系中，以暂时航迹的第一个点p1[x(1) y(1)]为圆心，以vmaxt、vmint为半径构建圆环形关联区域。如果在下一个扫描周期雷达在此区域内观测到新的点迹，则暂时航迹形成第2个点p2[x(2) y(2)]， 否则删除该暂时航迹。vmax、vmin分别

为目标运动的最大速度和最小速度,t为雷达的扫描周期。

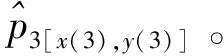
(21)

式中：

(22)

这里D3是服从自由度为m的χ2分布的随机变量。由给定的门限概率查表可得门限γ，若第3次扫描量测所得的最小D3min值小于γ，则对该D3min值所对应的量测点p3[x(3) y(3)]给予互联。此后重复步骤2)，从而完成目标检测。

通过M/N逻辑法可以实现对目标的检测，但是由于噪声点迹较密集的原因，可能存在检测到的航迹为噪声航迹的情况，所以需要对所有检测到的航迹进行进一步的判决。

2.2.2 基于径向速度方向判决的噪声航迹剔除

通过信号层处理可以对目标的多普勒频率进行估计，而在M/N逻辑法中并没有对目标的径向速度加以约束，所以可以将一部分径向速度不满足多普勒频率估计的航迹进行剔除，实现目标航迹的预估检测。

设k1、k2时刻的点迹坐标分别为(x1,y1)和(x2,y2)，则数据层对k2时刻目标的多普勒频率估计为

(23)

式中：sign(·)为取符号函数；λ为雷达工作波长。

由式(13)可以得到信号层对目标当前时刻的多普勒频率估计为

(24)

由于信号层对目标径向速度的估计精度较低，所以在此只根据所估计的多普勒频率方向进行判决。对每个时刻的航迹点进行如下判决：

对于某一条航迹而言，当速度估计矛盾的时刻数大于d时，判定航迹为噪声航迹，并予以剔除。

通过径向速度方向判决，一部分不满足判决要求的航迹被剔除，但同时需要注意的是，通过径向速度方向判决的方法并不能从根源上解决噪声航迹的产生问题。噪声航迹的产生来源于噪声点迹，只有通过调整滤波器的滤波中心以及带宽，才能减少噪声点迹的数量，从而降低噪声航迹产生的概率，所以，接下来对窄带滤波器的反馈调节环节进行构建。

2.3 基于反馈调节的联合处理

2.3.1 反馈调节的原因

由式(17)的分析可知，目标多普勒频率的估计精度直接影响着滤波器宽度的取值，进而影响到滤波效果的好坏，但是受采样频率等因素的影响，信号层对目标多普勒频率的估计精度较低，从而导致滤波效果较差，增大了数据层噪声航迹产生的可能性。

但同时，随着观测时间的延长，数据层能够得到较为准确的航迹径向速度估计，并且在一定时长后，能够将估计误差保持在较低的水平。因此，可以利用数据层对航迹径向速度估计的反馈对窄带滤波器的参数进行实时调整，从而使滤波效果更好，从根本上解决噪声航迹的产生问题。

2.3.2 基于数据层反馈信息的滤波器调节

设k时刻对目标的速度预测矢量V为

(25)

(26)

则V在τ方向上的投影为

(27)

投影的方差为

(28)

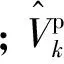
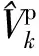
第k时刻滤波器中心坐标修正为

(29)

根据正态分布的“3σ”原则，将滤波器宽度修正为

(30)

通过式(29)和式(30)实现了利用数据层的反馈信息对滤波器参数进行实时调整。对于目标航迹而言，通过反馈可以使滤波器达到更好的滤波效果，从而减少噪声点迹对目标航迹的干扰；而对于噪声航迹而言，噪声点迹的减少会直接造成其航迹中断。

2.4 总体思路流程图

本文的射频噪声干扰抑制技术流程图如图5所示。

3 仿真实验

为了验证预估-反馈联合处理算法的有效性，本文从信号层算法、数据层算法以及反馈调节算法3部分对射频噪声干扰的抑制问题进行仿真实验，并与现有算法进行比较。

3.1 仿真条件设置

设雷达发射的LFM信号脉宽为50 μs，带宽为5 MHz，载频为5 GHz，中频为1 MHz，中频采样频率为15 MHz；雷达扫描周期为5 s，测距和测角误差分别为100 m和0.2°。射频噪声干扰信号的带宽为20 MHz，能够在频带上覆盖目标回波信号，目标参数信息如表1所示。

在雷达回波信号信干比为-25 dB条件下进行仿真实验。

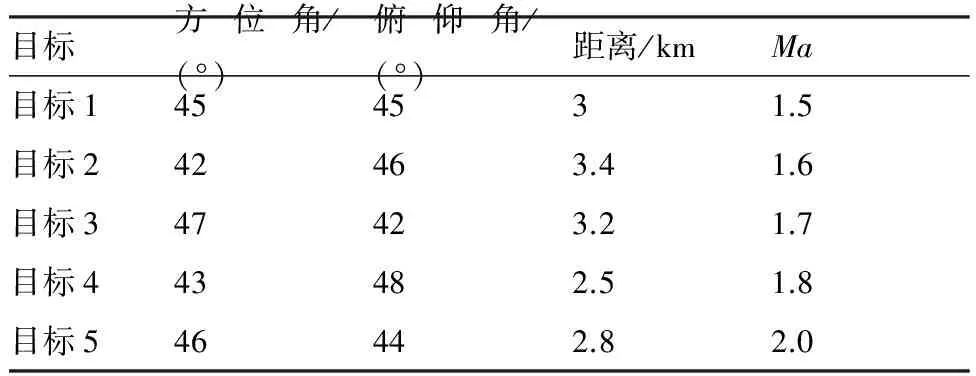
表1 目标参数Table 1 Target parameters

3.2 仿真结果与分析

3.2.1 信号层处理仿真验证

1)首先为验证本文信号层处理算法的有效性，与现有的基于峰值搜索的FRFT域滤波算法进行比较分析，其仿真结果如图6和图7所示。

图6为信干比为-25 dB条件下，LFM信号在FRFT域正交阶次的谱分布情况。由图6可以看出，信干比为-25 dB时，LFM信号在FRFT域的能量聚集点被完全淹没在噪声干扰中，无法通过峰值搜索的方法得到能量聚集点坐标。

图7为信干比为-25 dB条件下，通过子空间正交法得到的信号伪谱分布，其中，类似脉冲的尖峰代表复正弦信号所对应的角频率。由图7可以看出，信干比为-25 dB时，复正弦信号的角频率能够较准确的被估计出来，进而根据式(14)得到能量聚集点坐标。

表2所示为在不同信干比条件下，本文算法与峰值搜索算法的坐标估计均方根误差对比。

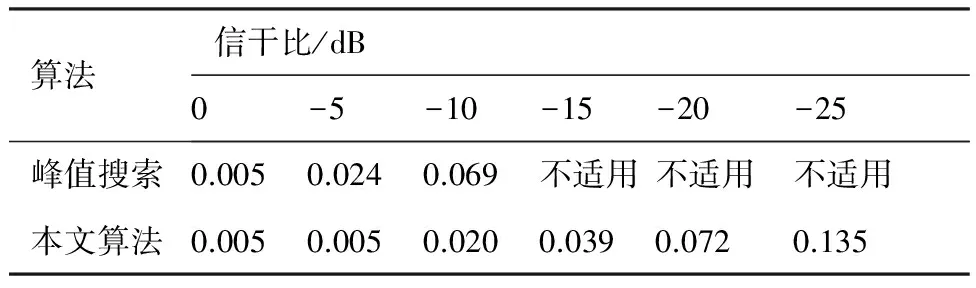
表2 与传统算法均方根误差(RMSE)对比

由表2数据可以看出，本文的坐标估计算法在估计精度以及稳定性方面均优于传统的峰值搜索算法。

通过以上仿真实验可以看出，相比于峰值搜索算法，本文所提算法抗噪声干扰能力更强，能够在信干比更低时实现LFM信号的检测和参数估计。

2)为进一步验证本文所提算法的有效性，对窄带滤波算法进行仿真验证，并给出了滤波前后的对比如图8和图9所示。图8(a)和图8(b)分别为窄带滤波前后的脉冲压缩结果，其中标注点表示目标所在位置。图9(a)和图9(b)分别为窄带滤波前后连续5个扫描周期所得到的点迹情况。

通过图8(a)和图8(b)的对比可以看出，本文算法在较好保留目标回波信息前提下滤除了大部分干扰信号；通过图9(a)和图9(b)的对比可以看出，窄带滤波之后所生成的点迹数量明显减少，从而有利于数据层对目标的检测。

结合本文算法，定义干扰抑制比为窄带滤波前后信干比的差值，则干扰抑制比随输入信号信干比的变化情况如图10所示。

图10中横坐标表示回波信号信干比，纵坐标表示干扰抑制比，随着信干比的增大，干扰抑制比的增大趋势逐渐减缓，并最终在信干比为35 dB时出现下降，其原因在于：回波信号信干比增大，使得LFM信号的载频估计误差增大，根据式(17)，滤波器的宽度逐渐增大，最终导致窄带滤波的干扰滤除效果下降。

3.2.2 数据层处理仿真验证

为验证本文数据层处理算法的有效性，对目标检测算法进行仿真验证。应用M/N逻辑法对窄带滤波之后连续5个扫描周期的点迹进行目标检测，仿真结果如图11所示。

图11为对连续5个扫描周期的点迹进行目标检测所形成的航迹情况。由图11可以看出，M/N逻辑法能够对目标进行检测，但同时，由于噪声点迹较密集分布在目标周围，所以一部分由噪声点迹形成的噪声航迹也被误检出来。

进一步对径向速度方向判决算法进行仿真验证，其仿真结果如图12所示。图12为根据径向速度判决对图10中的噪声航迹进行剔除后的结果。由图12可以看出，径向速度判决能够对一部分径向速度不满足判决条件的噪声航迹进行剔除，效果较为明显。

径向速度判决前后，噪声航迹的平均生成数量如表3所示。由表3可以看出，经过径向速度方向判决，噪声航迹的生成数量在很大程度上有所减少。同时仍有部分噪声航迹被保留下来，所以需要进一步通过数据层的反馈调节对噪声航迹进行剔除。

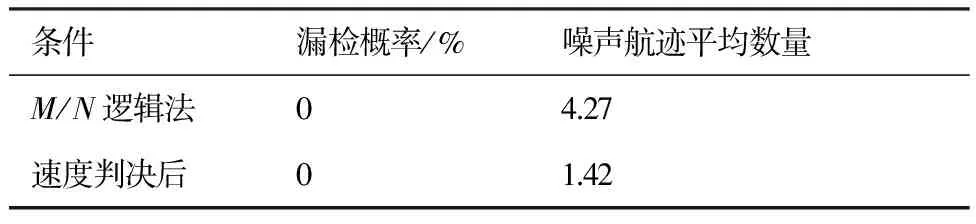
表3 噪声航迹数量对比Table 3 Comparison of noise track numbers

3.2.3 反馈调节仿真验证

为验证反馈调节的有效性，对滤波器在不同时刻的参数进行记录，其变化情况如表4所示。

表4为目标5的滤波中心以及滤波器带宽的变化情况，其中，LFM信号的能量聚集点坐标为1.736 8。由表4可以看出，加入反馈调节之后，滤波器的中心更加接近于能量聚集点坐标，并最终保持在很小的误差范围内，同时滤波器带宽也逐渐变窄，从而对噪声起到了较好的滤除效果。

为进一步验证反馈调节的有效性，对加入反馈调节之后数据层的目标检测情况进行仿真验证，其目标检测效果如图13所示。

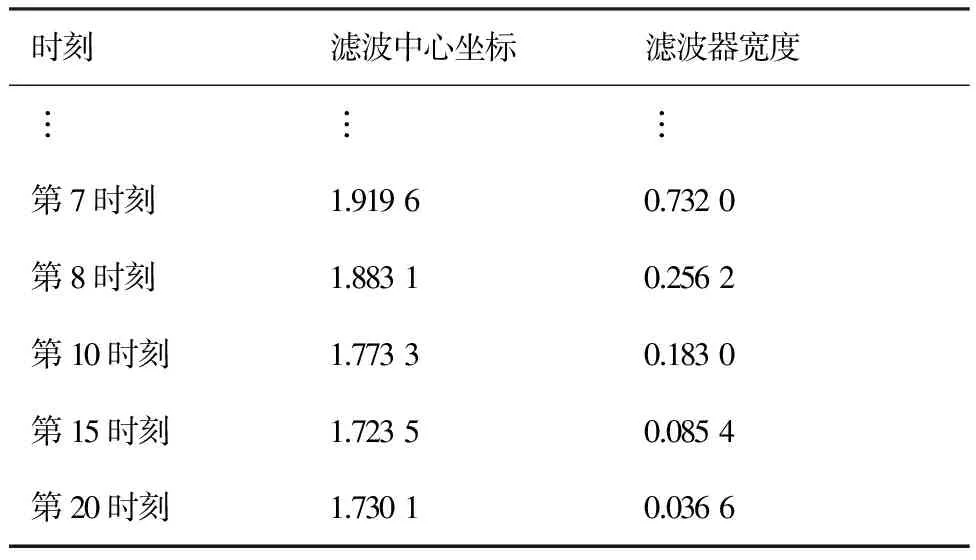
表4 滤波器参数Table 4 The filter parameter

图13为加入反馈调节之后的目标检测的结果。由图13可以看出，数据层的反馈调节对目标航迹没有产生影响，而对于噪声航迹而言，数据层的反馈直接导致了其航迹中断，可见，数据层的反馈调节能够起到较好的噪声航迹剔除作用。

将本文算法与文献[24]中算法的目标检测概率进行比较，蒙特卡罗实验次数为200次，实验结果如图14所示。

由图14可以看出，本文算法优于文献[24]中的算法，并且将压制干扰下的目标检测信干比提高了约10 dB左右，能够应用于信干比更低时的情况。

4 结 论

针对射频噪声干扰抑制问题，本文提出了一种预估-反馈联合处理算法。通过仿真实验证明了本文算法能够在信干比较低的情况下，实现对射频噪声干扰的抑制以及对目标的检测，并且该算法较传统算法具有更优的干扰抑制能力。

1)通过对信号层算法与数据层算法关联信息的提取以及反馈调节量的构建，实现了对射频噪声干扰的一体化抑制，有效提高了本文算法的干扰抑制能力。

2)利用数据层对目标径向速度的预测信息，合理构建能够调节信号层算法参数的反馈调节量，从而保证信号层处理算法的有效性和实时性。

3)通过仿真实验与文献[24]中基于Radon-分数阶傅里叶变换的算法进行了比较，证明了本文算法在射频噪声干扰环境中具有更好的目标检测能力。

参 考 文 献

[1] 赵国庆. 雷达对抗原理[M]. 西安: 西安电子科技大学出版社, 2012: 122-123.

ZHAO G Q. Radar countermeasure principle[M]. Xi’an: Xidian University Press, 2012: 122-123 (in Chinese).

[2] 李冬霞, 崔颜敏, 刘海涛, 等. 基于JADE的测距仪脉冲干扰抑制技术[J].系统工程与电子技术, 2016, 38(2): 423-427.

LI D X, CUI Y M, LIU H T, et al. Distance measure equipment impulse interference mitigation method based on JADE[J]. Systems Engineering and Electronics. 2016, 38(2): 423-427 (in Chinese).

[3] 温媛媛, 陈豪. 基于时域卷积盲信号分离的雷达干扰抑制技术算法[J].中国科学院大学学报, 2013, 30(4): 523-527.

WEN Y Y, CHEN H. Algorithm of radar interference suppression based on blind signal separation in the time domain[J]. Journal of University of Chinese Academy of Sciences, 2013, 30(4): 523-527 (in Chinese).

[4] JONEIDI M, ZAEEMZADEH A, REZAEIFAR S, et al. LFM signal detection and estimation based on sparse representation[C]∥Information Sciences and Systems. Piscataway, NJ: IEEE Press, 2015: 1-5.

[5] JIN Y, DUAN P, JI H. Parameter estimation of LFM signals based on scaled ambiguity function[J]. Circuits Systems & Signal Processing, 2016, 35(12): 1-18.

[6] DING Y, SUN L, ZHANG H, et al. A multi-component LFM signal parameters estimation method using STFT and Zoom-FRFT[C]∥IEEE International Conference on Communication Software and Networks. Piscataway, NJ: IEEE Press, 2016: 112-117.

[7] LIU D, LIU Y, CAI H, et al. Linear frequency-modulated continuous wave active sonar signal processing[C]∥OCEANS. Piscataway, NJ: IEEE Press, 2014: 1-5.

[8] 陈小龙, 关键, 刘宁波, 等. 基于FRFT的LFM信号自适应滤波算法及分析[J]. 现代雷达, 2010, 32(12): 48-53.

CHEN X L, GUAN J, LIU N B, et al. Adaptive filtering algorithm for LFM signal and performance analysis based on FRFT[J]. Modern Radar, 2010, 32(12): 48-53 (in Chinese).

[9] 贺达超, 王国宏, 孙殿星. 压制干扰下长基线雷达网多目标跟踪技术[J]. 指挥控制与仿真, 2015(6): 1-7.

HE D C, WANG G H, SUN D X. Multi-target tracking technique for long baseline radar network in the presence of suppressive jamming[J]. Command Control & Simulation, 2015(6): 1-7 (in Chinese).

[10] 王国宏, 李世忠, 白晶, 等. 压制干扰下组网雷达目标检测与跟踪技术[J]. 宇航学报, 2012, 33(12): 1781-1787.

WANG G H, LI S Z, BAI J, et al. Target detection and tracking technique for radar network in the presence of suppressive jamming[J]. Journal of Astronautics, 2012, 33(12): 1781-1787 (in Chinese).

[11] 李世忠, 王国宏, 白晶, 等. 压制干扰下雷达网点目标概率多假设跟踪算法[J]. 西安交通大学学报, 2012, 46(10): 101-106.

LI S Z, WANG G H, BAI J, et al. A tracking algorithm with multiple probabilities hypothesis for radar network point target in the presence of suppressive jamming[J]. Journal of Xi’an Jiaotong University, 2012, 46(10): 101-106 (in Chinese).

[12] 徐海全, 王国宏, 关成斌. 远距离支援干扰下的目标跟踪技术[J]. 北京航空航天大学学报, 2011, 37(11): 1353-1358.

XU H Q, WANG G H, GUAN C B. Tracking technique in the presence of standoff jamming[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011,37(11): 1353-1358 (in Chinese).

[13] 谢艾彤. 低信噪比信号的检测与参数估计方法研究[D]. 成都: 电子科技大学, 2007: 33-35.

XIE A T. Study on detection and parameter estimation of signal in low signal-to-noise ratio[D]. Chengdu: Electronic Science and Technology University, 2007: 33-35 (in Chinese).

[14] 杜东平. 雷达压制式干扰抑制算法研究[D]. 成都: 电子科技大学, 2008: 24-27.

DU D P. The research of radar pressure jamming suppression algorithm[D]. Chengdu: Electronic Science and Technology University, 2008: 24-27 (in Chinese).

[15] 李智明. 基于改进Fast ICA算法的混合语音盲分离[D]. 上海:上海交通大学, 2015: 21-43.

LI Z M. Blind separation of mixed audio signals based on improved fast ICA[D]. Shanghai: Shanghai Jiao Tong University, 2015: 21-43 (in Chinese).

[16] 齐林, 陶然, 周思永, 等. 基于分数阶Fourier变换的多分量LFM信号的检测和参数估计[J]. 中国科学, 2003, 33(8): 749-759.

QI L, TAO R, ZHOU S Y, et al. Detection and parameter estimation of multi-component LFM signals based on fractional Fourier transform[J]. Science in China, 2003, 33(8): 749-759 (in Chinese).

[17] 刘锋, 徐会法, 陶然. 基于FRFT的对称三角LFMCW信号检测与参数估计[J]. 电子与信息学报, 2011, 33(8): 1864-1870.

LIU F, XU H F, TAO R. Detection and parameter estimation of symmetrical triangular LFMCW signal based on Fractional Fourier transform[J]. Journal of Electronics & Information Technology, 2011, 33(8): 1864-1870 (in Chinese).

[18] 陶然, 邓兵, 王越, 等. 分数阶傅里叶变换及其应用[M]. 北京: 清华大学出版社, 2009: 11-12.

TAO R, DENG B, WANG Y, et al. Fractional Fourier transform and its applications[M]. Beijing: Tsinghua University Press, 2009: 11-12 (in Chinese).

[19] 张贤达. 信号处理中的线性代数[M]. 北京: 北京科学出版社, 1997: 65-67.

ZHANG X D. Linear algebra in signal processing[M]. Beijing: Beijing Science Press, 1997: 65-67 (in Chinese).

[20] 张峰, 陶然. 分数阶Fourier域谱估计及其应用[J]. 电子学报, 2008, 36(9): 1723-1727.

ZHANG F, TAO R. Power spectral estimation and its application in Fractional Fourier domain[J]. Acta Electronica Sinica, 2008, 36(9): 1723-1727 (in Chinese).

[21] 王瑜, 李小波, 周青松, 等. 基于FRFT窄带滤波的LFM信号研究[J]. 火力与指挥控制, 2016, 41(12): 41-43.

WANG Y, LI X B, ZHOU Q S, et al. Study of LFM signal based on FRFT domain narrowband filter[J]. Fire Control & Command Control, 2016, 41(12): 41-43 (in Chinese).

[22] 何友, 修建娟, 张晶炜, 等. 雷达数据处理及应用[M]. 北京: 电子工业出版社, 2010: 117-118.

HE Y, XIU J J, ZHANG J W, et al. Radar data processing with applications[M]. Beijing: Electronic Industry Press, 2010: 117-118 (in Chinese).

[23] 孙殿星. 雷达网抗欺骗式干扰技术研究[D]. 烟台: 海军航空工程学院, 2015: 81-82.

SUN D X. Research on anti-spoofing technology of radar network[D]. Yantai: Naval Aeronautical and Astronautical University, 2015: 81-82 (in Chinese).

[24] 陈小龙, 刘宁波, 王国庆, 等. 基于Radon-分数阶傅里叶变换的雷达动目标检测方法[J]. 电子学报, 2014, 42(6): 1074-1080.

CHEN X L, LIU N B, WANG G Q, et al. Radar detection method for moving target based on Radon-fractional Fourier transform[J]. Acta Electronica Sinica, 2014, 42(6): 1074-1080 (in Chinese).