系留四旋翼无人飞行器滑模控制算法研究

李中健，杨宸骅，朱亚龙

（西北工业大学自动化学院，陕西西安710129）

近几年，由于四旋翼无人飞行器结构简单、操作容易、成本低廉、便于搭载各种相关设备，它已经逐渐成为控制领域研究的一大热点。目前市面上常见的四旋翼无人飞行器已经被广泛用于航拍[1]、低空地貌测绘、大气质量监测[2]、森林火灾预警、交通情况空中监管等。但目前常用的锂电池供电形式限制了四旋翼无人飞行器的结构大小，并且导致其有效载荷较小，只能搭载一些轻质设备，无法长时间连续工作，这极大的限制了四旋翼无人飞行器的发展潜力[3]。系留四旋翼无人飞行器通过系留缆绳为飞行器及其搭载的仪器提供电能，这样的供电形式就不再限制其电机和螺旋桨的选择以及结构大小，完全可以依据载重需求来进行系留四旋翼无人飞行器的设计，并且具有结构简单、机动性好、成本低廉、方便搭载设备等诸多优点。

文中采用“质量集中-轻质钢杆”模型进行系留缆绳建模，并利用牛顿欧拉方程[4]对四旋翼飞行器进行受力分析，在此基础上将系留绳模型和四旋翼飞行器模型有效结合起来，建立了系留四旋翼无人飞行器的数学模型，并且利用滑模控制算法实现对系留四旋翼的较好控制[5]。

1 系留四旋翼结构特点与飞行原理

系留四旋翼无人飞行器主要由四旋翼飞行器、系留缆绳以及地面装置3部分组成，如图1所示。四旋翼无人飞行器具有相邻转向相反，相对转向相同的四个电机，并依靠4个电机转动的速差姿态变化。系留缆绳是四旋翼飞行器与地面装置的连接线，由传输光纤、导线、保护层、承力层等组成。它一方面需要实现四旋翼飞行器平台上各种仪器设备与地面站之间的实时数据传输，另一方面也要为空中的四旋翼飞行器平台及其搭载的各种仪器设备持续的供电。

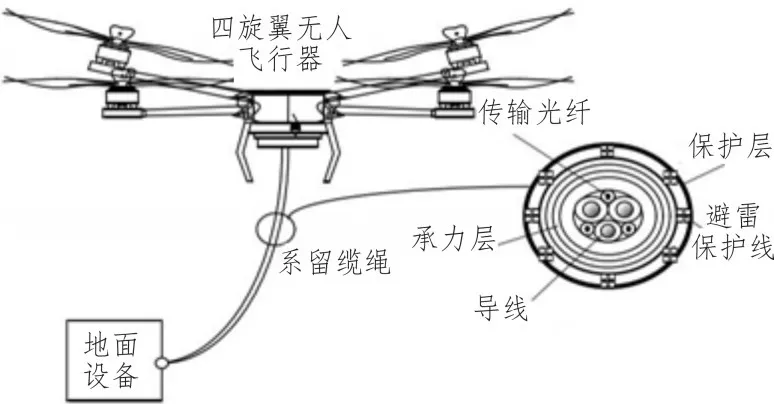
图1 系留四旋翼无人飞行器结构组成

2 动力学模型建立

2.1 系留缆绳模型建立

本文采用“质量集中-轻质钢杆”模型来建立系留缆绳的数学模型，认为系留缆绳是由无数个轻质钢杆和质量节点组成。在系留缆绳上任取一微元段进行受力分析，以取得第i个微元段为例，它上下端点的拉力Ti、Ti-1以及重力Gi和风力Qi作用下处于平衡状态，如图2所示。

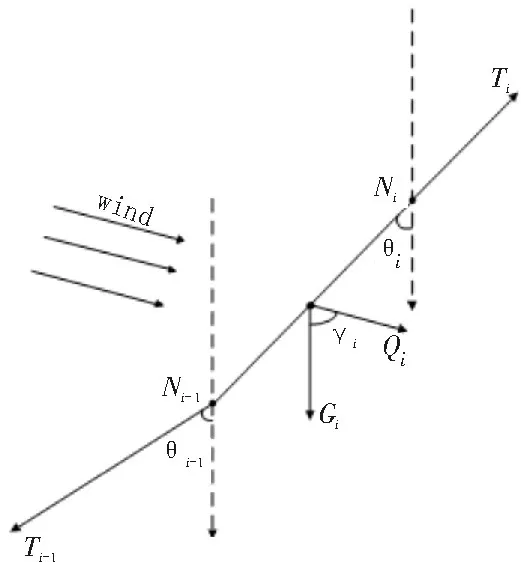
图2 系留缆绳第i个微元段受力图

Ni端的缆绳拉力Ti与Z轴的夹角为。第i个微元段系留缆绳自身重力Gi作用于缆绳中点，风力Qi也作用于系留缆绳中点。可得：

给定系留点处的拉力大小为T0，方向角为θ0，缆绳总长L和所分微元段N后，对每个微元段进行受力分析，同时考虑微元段间的受力传递。可确定系留点的坐标：

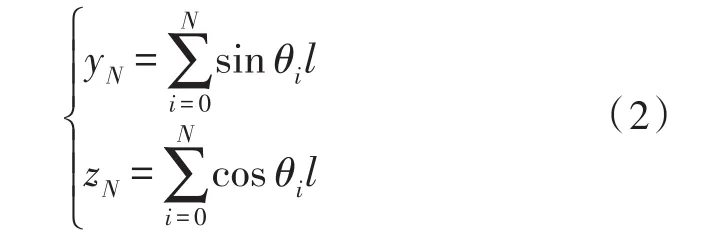
2.2 系留四旋翼动力学模型建立

系留四旋翼无人飞行器上的作用力主要包括系留缆绳的拉力Tn、旋翼升力T和旋翼扭转力矩M，以及飞行器自身的重力G。假设系留缆绳拉力在地面坐标系yeOeze平面内，系留缆绳拉力Tn与地面坐标系ze的夹角为θn，在机体坐标系下系留四旋翼无人飞行器低速飞行状态时所受到的力和力矩如图3所示。

图3 系留四旋翼飞行器所受力与力矩分析

作用在飞行器上的力和力矩在机体坐标系各轴上的分量之和为

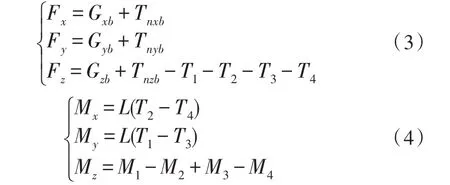
由牛顿第二定律，可知系留四旋翼无人飞行器在机体坐标系建立运动方程为：

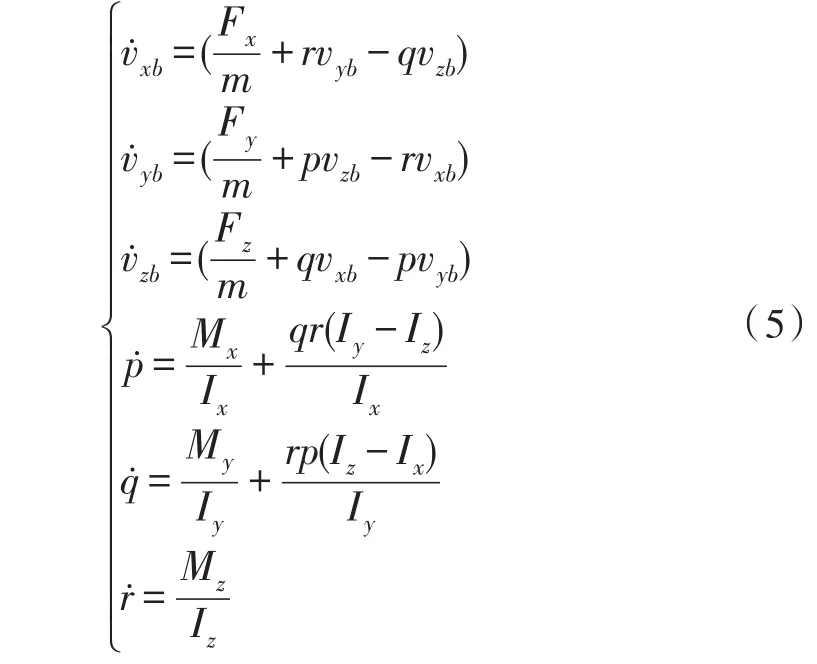
3 控制器设计

高度控制回路和姿态控制回路的设计如图4所示，控制器的输入为期望的高度zd和期望的滚转角ϕd、俯仰角θd、偏航角ψd。控制部分由高度控制器和3个姿态控制器组成，经过系统的动态模型处理之后的输出信号又同时作为反馈信号反馈给滑模控制器[6-9]。

3.1 高度控制器设计

滑模控制系统的设计步骤一般可以分为切换函数s(x)的设计与滑动模态控制器的设计。切换函数是按照某种期望的动态特性来设计的，要使得它确定的滑动模态具有某些优良的动态品质并且需要是渐进稳定的。滑动模态要满足到达条件式，滑动模态控制器需要能够在切换面附近产生滑动模态的控制输入，使得系统的状态点在有限时间内到达切换面[10-13]。

在系留四旋翼无人飞行器高度控制器设计时，由于仅考虑高度信息，所以只需对垂直通道进行研究，即：

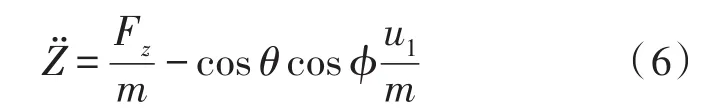
定义高度的跟踪误差变量为：eZ=z-zd其中，z和zd分别为飞行器的实际飞行高度和期望飞行高度。定义滑模面为：s=̇Z+λeZ，由滑模控制理论可知，λ>0且为常数，s的值在滑模面附近趋于0，由此可得，在滑模面附近：̇Z=-λeZ，为确保滑模面在平衡点附近为全局渐进稳定的，定义李雅普诺夫函数，对其求导得：

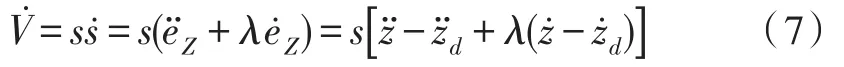
图4 系留四旋翼飞行器的滑模控制模块示意图

在系留四旋翼无人飞行器稳定飞行时：

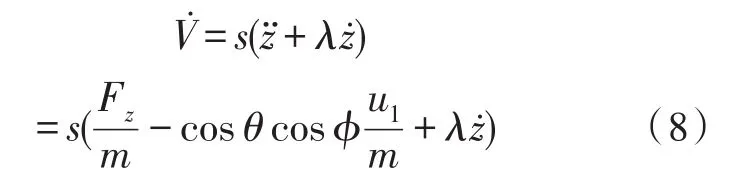
在考虑气流扰动等有界干扰的情况下，设系留四旋翼无人飞行器稳定飞行时受到的有界干扰为，其中a为大于 0的常数[14]，则有：

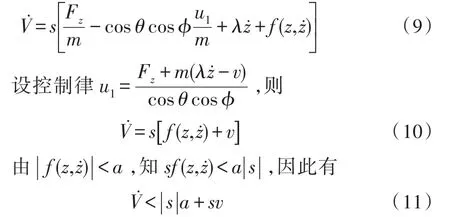
令v=-ρsgn(s)，其中，ρ为大于0的常数，且ρ>a；sgn(s)=s/|s|，所以式（11）可化为：

因为ρ>a，|s|>0，知。因此，滑模控制律u1可以满足李雅普诺夫稳定定理，飞行器可在有限的时间内到达设定高度。即

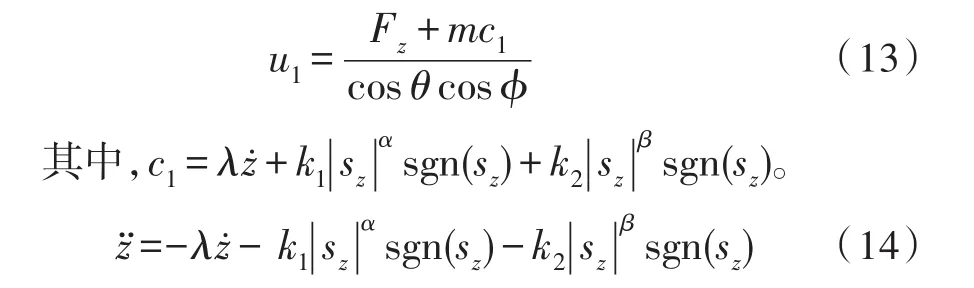
选择合适的λ和ρ值即可使飞行器在有限的时间内到达设定高度。

3.2 姿态控制器设计

以飞行器滚转角为例，其滑模控制器设计过程如下[15-19]：

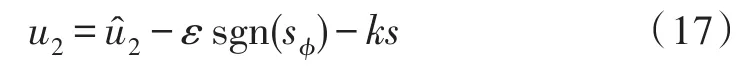
其中，ε，k均为大于0的常数。定义李雅普诺夫函数为，得：

所以，在控制律（17）式的作用下，滚转角将在有限时间内到达滑模面。因为滑模控制信号属于非线性，其主要缺点是抖振较大，为了减小抖振，减小抖振对系统性能的负面影响，加快趋近速度，本文采用双幂次趋近率，即：

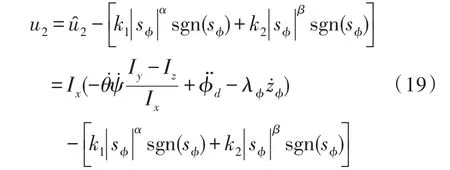
其中，α，β，k1，k2均为大于0的常数。有：

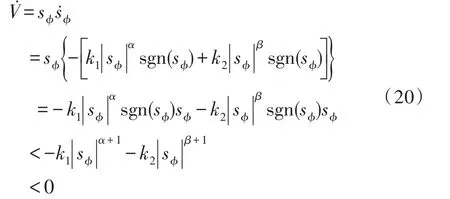
因此，在控制律式（19）作用下，滚转角一定可以在有限时间内到达滑模面。u3、u4的求解方法与u2的求解方法类似，

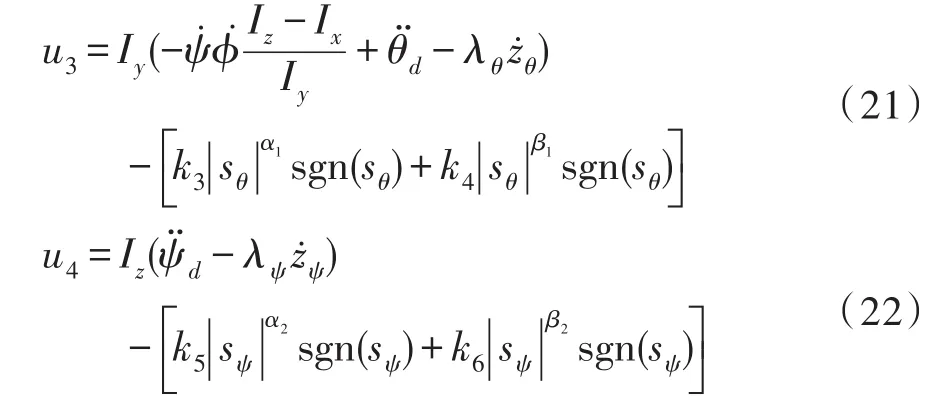
4 仿真实验与设计

4.1 无干扰系统仿真

假设系统不含参数摄动和外界干扰的情况下进行，本文取参数为：k1=k3=5，k2=k4=7，k2=k4=7，k5=6.5，k6=9，ε=0.01，α=0.5，β=0.2 。如图5所示高度阶跃响应曲线，高度的阶跃响应上升时间为1.9 s，没有超调产生，调节时间为2 s，在调节过程中没有出现震荡，并且系统在2.3 s达到稳定状态，之后在没有外界干扰的情况下一直可以保持稳定状态，整体控制效果较好。

图5 飞行器高度阶跃信号控制效果

如图6所示3个姿态角ϕ、θ、ψ的阶跃响应曲线，由图6可知，通过滑模方法为姿态角设计的控制系统可以使姿态角的阶跃响应曲线不出现超调、震荡，姿态角在1 s左右便可达到稳定状态。

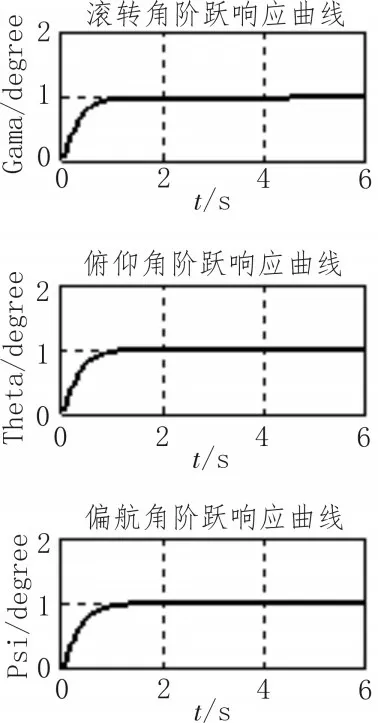
图6 飞行器姿态角阶跃信号控制效果

4.2 有干扰系统仿真

系留四旋翼无人飞行器在外加干扰信号作用下，随着添加的干扰信号增强，高度和3个姿态角均出现了逐渐增强的上下震动。当干扰信号较弱时，对系统稳定性基本不产生影响，高度和3个姿态角均能迅速恢复稳定。当干扰信号较强时，在过渡时间内，由动作值的幅度相对较大，变化幅度也较大，高度和3个姿态角恢复稳定需要的时候变长，也会产生一定的震荡，但最终高度和3个姿态角均能回到了稳定状态，说明该高度和姿态控制系统具有一定的稳定性和抗干扰能力。高度和姿态角的抗干扰滑模控制仿真结果如图7、图8所示。

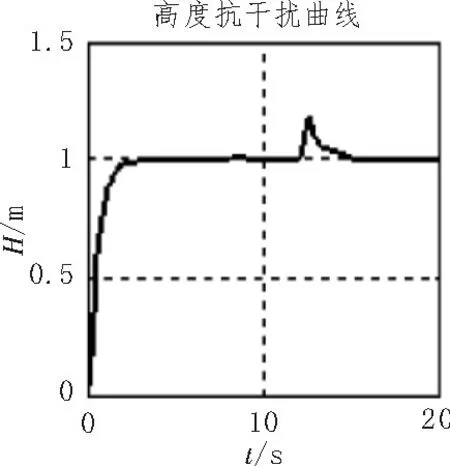
图7 飞行器受到干扰时高度的滑模控制效果

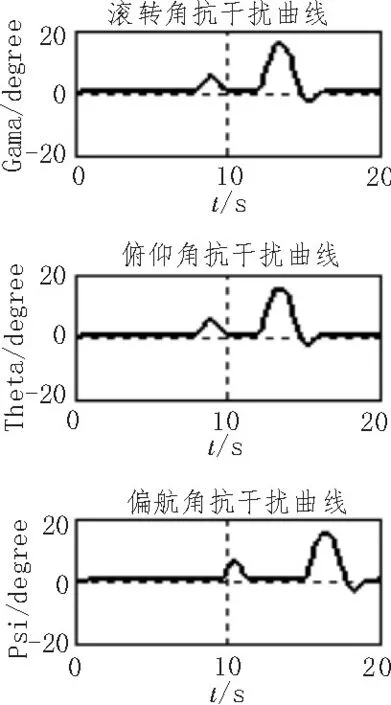
图8 受到干扰时姿态角的滑模控制效果

4.3 参数改变系统仿真

本文模拟了在飞行器质量和转动惯量改变时的飞行器跟踪方波信号的飞行情况，将飞行器的质量减小30%，X轴和Z轴上的转动惯量增加30%，Y轴上的转动惯量减小30%，控制指令为一个方波信号，最终飞行器的姿态角跟踪控制效果如图9所示。

由以上仿真曲线可知，当系留四旋翼无人飞行器系统自身的参数大幅度改变时，滑模控制器对3个姿态角的控制性能均有所衰减，系统的调节时间以及稳定所需要的时间均有所增加，出现一定的超调，在调节过程中也没有出现震荡，最终3个姿态角均可以达到期望值，且最终稳定之后基本没有出现静差。

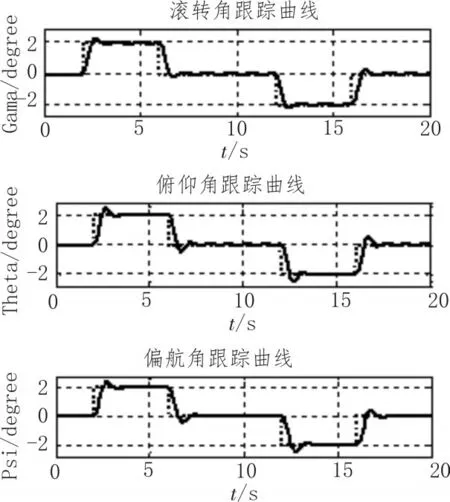
图9 数改变时姿态角滑模控制效果

5 结论

本文对系留四旋翼无人飞行器的建模与控制进行了研究。首先通过对系留缆绳、系留四旋翼无人飞行器的数学建模与分析，然后利用滑模控制算法完成系留四旋翼无人飞行器控制系统的研究设计，最后进行悬停与轨迹跟踪的仿真分析。在存在外界干扰或情况下，滑模控制算法表现出较好的稳定性；在自身参数改变的情况下，该系统表现出一定鲁棒性。因此，采用该滑模控制算法设计的系留四旋翼无人飞行器控制系统在一定程度上可以消除载荷改变及机体受损带来的影响。

参考文献：

[1]王景志.多无人机协同安全通信策略研究[D].沈阳：沈阳航空航天大学，2015.

[2]武文斌.带有输入限制的自适应控制在无人机上的应用[D].北京：北京理工大学，2015.

[3]张鹏.基于STM32的有缆多旋翼飞行器控制系统研究[D].南昌：南昌航空大学，2016.

[4]叶树球，詹林.基于PID的四旋翼飞行器姿态控制系统[J].计算机与现代化，2015（5）:117-120.

[5]胡盛斌，陆敏恂，陆文华.基于积分滑模面的飞机姿态模糊滑模控制[J].系统仿真学报，2013，25（3）:530-534.

[6]杨兴明，李文静.基于滑模控制器的四旋翼飞行器控制[J].合肥工业大学学报：自然科学版，2016（7）:924-928.

[7]Gonzalez I，Salazar S，Lozano R，et al.Real-time altitude robust controller for a Quad-rotor aircraft using Sliding- mode control technique[C]//International Conference on Unmanned Aircraft Systems.2013:650-659.

[8]李波波，贾秋玲.基于滑模控制的四旋翼飞行器控制器设计[J].电子设计工程，2013，21（16）:76-78.

[9]张燕，陈林奇，盛洲.移动机器人控制系统的设计[J].工业控制计算机，2017，30（1）:18-20.

[10]王建敏，吴云洁，董小萌.基于滑模干扰观测器的高超声速飞行器滑模控制[J].航空学报，2015，36（6）:2027-2036.

[11]Drouot A，Richard E，Boutayeb M.Hierarchical backstepping-based control of a Gun Launched MAV in crosswinds:Theory and experiment[J].Control Engineering Practice，2014，25（25）:16-25.

[12]陈航科，张东升，盛晓超，等.四旋翼飞行器悬停状态姿态控制建模与仿真[J].计算机仿真，2013，30（11）:41-45.

[13]捷联式导引头控制算法研究[D].哈尔滨：哈尔滨工业大学，2015.

[14]刘锦涛，吴文海，李静，等.四旋翼无人机SO（3）滑模变结构姿态控制器设计[J].控制与决策，2016，31（6）:1057-1064.

[15]Besnard L，Shtessel Y B，Landrum B.Quadrotor vehicle control via sliding mode controller driven by sliding mode disturbance observer[J].Journal of the Franklin Institute，2012（349）:658-684.

[16]Khelfi M F，Kacimi A.Robust control with sliding mode for a quadrotor unmanned aerial vehicle[C]//IEEE InternationalSymposium on Industrial Electronics.IEEE，2012:886-892.

[17]Luque-Vega L，Castillo-Toledo B，Loukianov A G.Robust block second order sliding mode control for a quadrotor[J].Journal of the Franklin Institute，2012（349）:719-739.

[18]淡鹏，陈剑平.自旋卫星几何定姿限制条件及误差分析[J].电子科技，2016（5）:62-66.

[19]杨逸，梁婧.卫星通信技术在电力应急通信抢修中的应用[J].电力信息与通信技术，2014（12）:34-38.