基于改进模板匹配算法的伤票识别与定位

蒋昭颖，郝福珍

（华北计算技术研究所后勤信息化事业部，北京100083）

伤票是医疗单位记录伤员受伤信息和统计伤员出现的病情，救治伤员过程的记录承载方式，是卫生机构医疗单位做统计汇总信息的主要参考样本，也是后勤单位保障工作经验总结与医学研究的重要资料和数据[1]。伴随着我国军事化改革的浪潮不断兴起以及后勤单位医护保障系统的阶段性革新，纸质化伤票逐渐采用电子化手段进行保存和使用，电子化、信息化、网络化、智能化成为了伤病员管理方式的新趋势[2]。采用图像识别技术，将纸质伤票的信息提取并存入后台数据库中。经过这一系列的操作，既保证了医护人员在紧急情况下对伤病员信息的处理，又可以实现高效的后勤保障服务。由此可见，纸质伤票的电子化管理在伤病员信息化管理方面占有举足轻重的地位。

1 图像识别技术

文中主要研究伤票图像识别定位算法，该算法的复杂性在于伤票图像的广泛差异性。这种差异来自于光照条件、拍照角度以及破损情况等。而且图像中的伤票往往嵌入在混乱的场景和背景中，镜头本身的抖动也会对处理结果产生影响。文中通过模板匹配的方法对伤票进行识别粗定位，并且对其中的相关系数法进行改进，提升算法速度及准确率，采用数学形态学方法对伤票边缘集合特征进行精确定位，并与模板图片进行匹配度验证。

2 改进相关系数匹配法粗定位

伤票识别的匹配策略分为两种，一种是完全匹配，即两幅图像的特征完全相同，另一种是按照相关性匹配，即两幅样本的感兴趣部分之间的距离小于某一个设定好的数值，这两种办法是当今时代图像辨识范畴内最常用的算法。

2.1 归一化互相关匹配原理

在匹配算法中，归一化互相关匹配算法是应用非常多的一种方法，非常典型。在该方法中，我们需要计算出两幅图片的互相关程度，从而得到采集的伤票图像与模板的样本二者的匹配关系。归一化互相关值的计算与选择的二维数组模板有关，不同的位置将会在该范围内计算出不同的互相关值，从而决定该位置是否为最佳位置。互相关有两种定义形式，分别为：

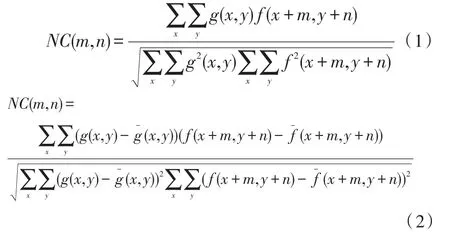
归一化互相关算法具有高精度和适应性，在互相关计算中，图像的自相关值相对较大，相似度形成相对于模板的真实位置相对平缓的峰值，但是不能精确地检测峰值位置。换句话说，当模板划痕图像偏离真实位置时，图像相关值较大，这使得难以确定模板图像在实际损伤图像中的精确位置。归一化互相关算法的缺点是计算复杂度高，计算时间长。

2.2 归一化互相关匹配实例

在160×160的滑动窗口内，首先计算模板的均值，然后计算样本的均值。模板像素值与均值做差，同时样本像素值与样本均值做差，二者相乘，将窗口内每一位置处的该数值进行累加，这个累加值就是归一化相关系数法的分子。分母的计算如下：模板像素值与均值做差，然后将该差值做平方运算，累加窗口内的每一位置处的平方值。同时按相同的方法计算样本像素值与均值做差，并平方之后累加。二者相乘然后进行开方运算，得到的就是该位置处的归一化相关系数。归一化相关系数匹配效果图，如图1所示。

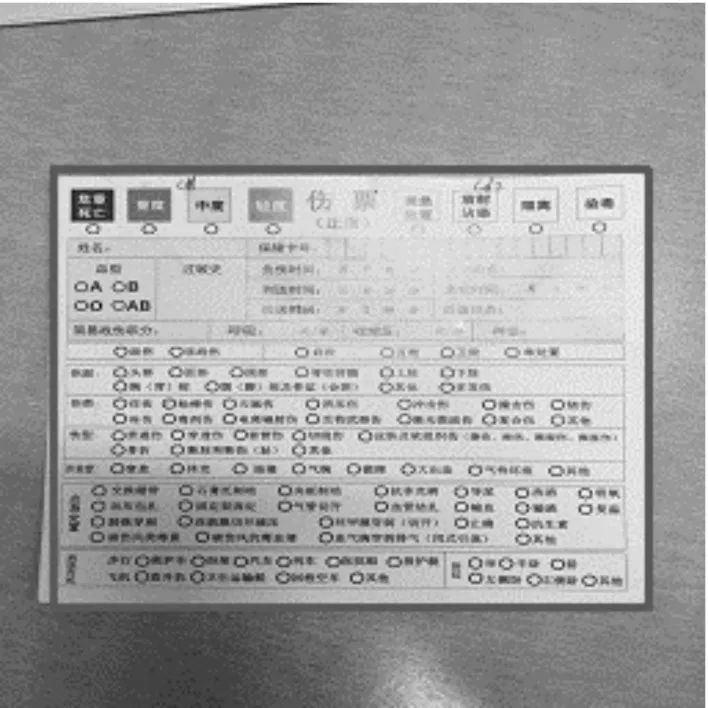
图1 归一化相关系数匹配效果图

我们将每一位置处的归一化相关系数以及行值和列值用一张三维图来形象的表示，能够发现归一化相关系数的值均在0～1范围内，且能够发现最大的归一化相关系数就是最佳的匹配位置。归一化相关系数匹配法各坐标点处的相关系数三维图，如图2所示。

通过归一化相关系数图，我们可以得到在伤票采集图像中的最大归一化相关系数的位置，从而可以得到最佳匹配位置。

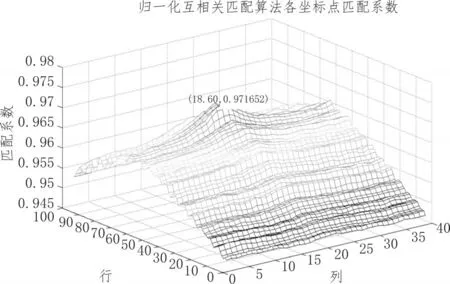
图2 归一化相关系数匹配法相关系数图

表1 归一化相关系数匹配算法分析

2.3 相关系数匹配法改进

对式（2）进行化简，得式（3）

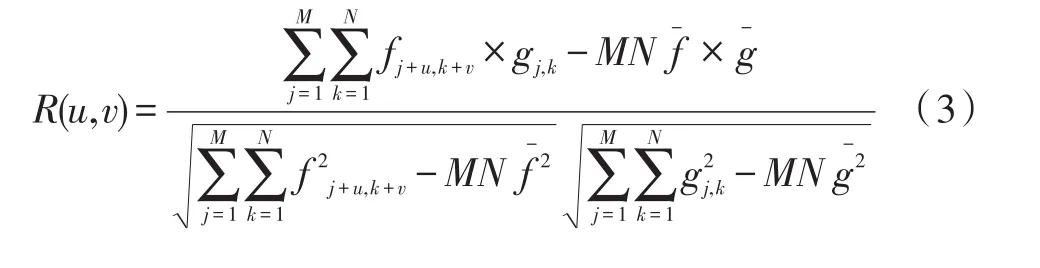
在不影响相似性度量的前提下，对（3）式进行相关系数近似计算。本文从两方面对相关系数计算进行改进，一方面从公式的近似和化简，另一方面从计算量和搜索位置进行改进。

2.3.1 算法理论层面改进

该算法结合顺序相似性检测算法（SSDA）算法的思想进行改进。SSDA是基于匹配操作的思想，然后给出一种阈值计算方法。阈值可以随着匹配操作的进行而被调整，并且它可以反映匹配操作是否可能超过阈值结果。因此，可以在每个匹配操作的过程期间的任何时间检测匹配操作是否继续。归一化互相关匹配方法在计算上较大的原因是搜索窗口在捕获的票图像上跳过并且每次滑动执行匹配相关计算。而且，除匹配点外，其他非匹配点并不需要进行运算，但是归一化相关匹配在每一点都进行了相关计算，这就导致了图像匹配算法的计算耗费大量增加，对实际的匹配影响却并没有很大。综上所述，SSDA的思想就是如果找到模板定位的目标像素点为非准确像素点就果断丢掉，停止计算，立即换到新的像素点位置计算，采用这样的思路，能够大幅度提高算法的实时性。

具体实现该算法的过程如下：我们利用SSDA的思想改进归一化相关系数匹配算法，需要明确SSDA选择开关值的算法策略。选择二维数组窗口，利用该窗口内的像素值依次计算该位置的归一化相关系数，同时每经过一次计算需要与SSDA的开关值进行比较，如果计算完的数值超过了开关值，则认为该位置处的二维窗口的归一化相关系数与开关值不一致，即该位置的二维窗口为无效窗口，停止接下来的计算，进行下一个位置处搜索窗口的计算，该思想能够完成匹配算法的加速。

2.3.2 模板图像匹配搜索位置的优化

文中，模板的大小为420×420，采集图片大小为640×480，针对模板与采集图片大小，我们对搜索位置进行优化。由于在扫描伤票过程中，伤票位置均处于屏幕的中间区域，所以，搜索的位置我们从图片的1/3处开始搜索，直至图片的2/3处结束。两条红线为搜索范围，蓝色矩形为起始模板位置，黄色矩形为终止模板位置。我们只需要搜索1/3图片区域即可找到是否有匹配的区域，通过该算法，可以将匹配运算时间提高2/3。

由于文中在场景中只需要寻找伤票，所以，为了提高运算效率，不需要每个点都进行计算，文中采取的方法是隔一个点进行一次运算，这样只需要进行(M×N)/4次加法运算，运算效率可以大幅提高。

图3 改进算法各坐标相关系数

通过改进相关系数法我们发现，通过门限值的设定，该算法只需搜索120个点的位置，即可找到最佳匹配位置。而传统的匹配算法需要搜索3 744个点，通过处理时间的分析，我们也可以发现改进的算法大大减少了匹配处理时间，79 ms的处理时间也满足伤票的实时检测需求。

表2 改进的匹配算法分析

在粗定位前，首先进行模板匹配，判断场景中是否存在伤票，并且获取模板位置。对采集的伤票分别采用传统相关系数匹配与改进的相关系数匹配法，其实验结果如图4所示，算法耗时比较如表2所示。

表3 两种算法耗时比较

3 基于边缘几何特征精确定位

模板匹配能够得到复杂场景中伤票的大体位置，该区域可以作为ROI区域，由于伤票最终的目的是要提取出选中信息，所以需要精确定位伤票并且将其每点坐标映射到二维直角坐标系中，便于定位选中点信息。所以，本文给出基于边缘几何特征的数学形态学算法进行伤票的精确定位。

数学形态学最早由Martin提出，并广泛应用于图像处理领域[7]。所提出的基于边缘几何特征的数学形态学算法依据ROI区域中伤票的大小和结构，利用开操作和闭操作将不含有伤票信息的候选区域滤除并最终得到伤票精确定位点。综合考虑影响伤票精确定位的主要因素，主要包括在拍摄伤票过程中可能出现的外界干扰因素：例如曝光过度、阴影遮挡等。使用自适应阈值算法，能够获得稳定的伤票定位结构。

3.1 图像预处理

为了解决阴影和光照条件下会造成阈值的误分割这一问题，我们需要采用自适应局部阈值分割方法。本文采用中值滤波和加权平均法实现自适应阈值的计算实现图像的二值化。

自适应局部阈值的原理是在需要确定门限值的位置选取一个模板窗口，根据模板窗口内的所有灰度值，动态计算出一个阈值作为该位置处的门限值。这种方法能够避免全局阈值法单一门限值的缺陷，特别适用于在图片各点光照不均匀的情况使用。即用规范之后的像素亮度值来进行图片的光照补偿，根据规范化的像素值决定该点是黑色像素还是白色像素。文中采用该方法进行阴影区域的消除以及曝光过度区域的补偿。第一步，将图片分块，计算每个区域的灰度像素直方图。然后，计算每一个区域的门限值，所求位置处的门限值需要结合相邻区域的门限值进行插值获取。

对采集的图片进行固定阈值分析以及自适应阈值分析，结果如图4所示。可以发现，固定阈值无法兼顾光照和阴影的补偿，左下角部分受阴影的影响，导致选取的阈值过高，右上角部分受光照的影响，导致选取的阈值过低，无法得到清晰完整的二值图片。而自适应阈值可以很好的补偿光照和阴影的缺陷，恢复完整图像。

图4 固定阈值与自适应阈值对比图

3.2 边缘几何特征拟合矩形

在文中研究的伤票中，我们人为指定的标志块为矩形，所以本文对闭合边缘曲线进行矩形拟合。对于二维平面内的任意矩形，可以用5个参数对其进行唯一定位和描述，重心位置（x，y)，矩形4个顶点坐标P1(x，y)，P2(x，y)，P3(x，y)，P4(x，y)。

首先，采用矩的方法对拟合矩形的重心位置（x，y)进行估算，公式如下[35]：

其中，f(x，y)为权值，当统计点 (x，y)在闭合曲线所围区域内时取1，否则取0，M、N为闭合曲线所围区域的最小外接矩形的长和宽，可以通过各轮廓点坐标得到，S为闭合区域面积，mij为矩形区域内像素点位置(i+j)阶原点矩，其中(m01，m10)为闭合区域的重心位置。

得到矩形重心位置后，遍历轮廓边缘坐标，计算重心与每一个边缘坐标的绝对距离，选取距离最大的 4 个点，分别为P1(x，y)，P2(x，y)，P3(x，y)，P4(x，y)。再对其4个顶点坐标进行排序，令其按照左上、左下、右上、右下的顺序进行存储。

对数学形态学处理后的图片进行矩形拟合，我们将闭合曲线所围区域用实心表示，然后对其进行矩形拟合，选取左上角、右上角和下方拟合矩形结果，处理结果如图5所示。

图5 提取轮廓效果图和矩形拟合效果图

得到拟合矩形后，提取左上角点坐标、右上角点坐标、左下角点坐标、右下角点坐标进行透视变换，将其映射到二维平面上，对其进行提取信息操作。

4 结论

文中采集各种场景下的伤票进行伤票自动识别实验。伤票自动识别检测是在手持机Android4.2系统中运行，结合Opencv2.4.9所实现的。通过检测伤票的边缘几何特征，基于改进模板匹配算法的伤票识别与定位的方法，精确度高，鲁棒性强，适用于各种复杂场景中识别并定位伤票。算法对相关系数匹配法进行改进，针对其速度慢的缺点进行算法上的优化，优化效果明显，速度可以大幅提高。采用自适应阈值的方法消除曝光过度和阴影对伤票检测影响，实验表明，自适应阈值能够完全补偿曝光和阴影。采用数学形态学的方法对伤票边缘进行封闭连接，保证伤票的3个标记块位置处的区域时闭合的。采用基于边缘特征的矩形拟合方法，对标记块进行矩形拟合，精确得出伤票的4个角点，从而定位伤票位置，便于后续研究。

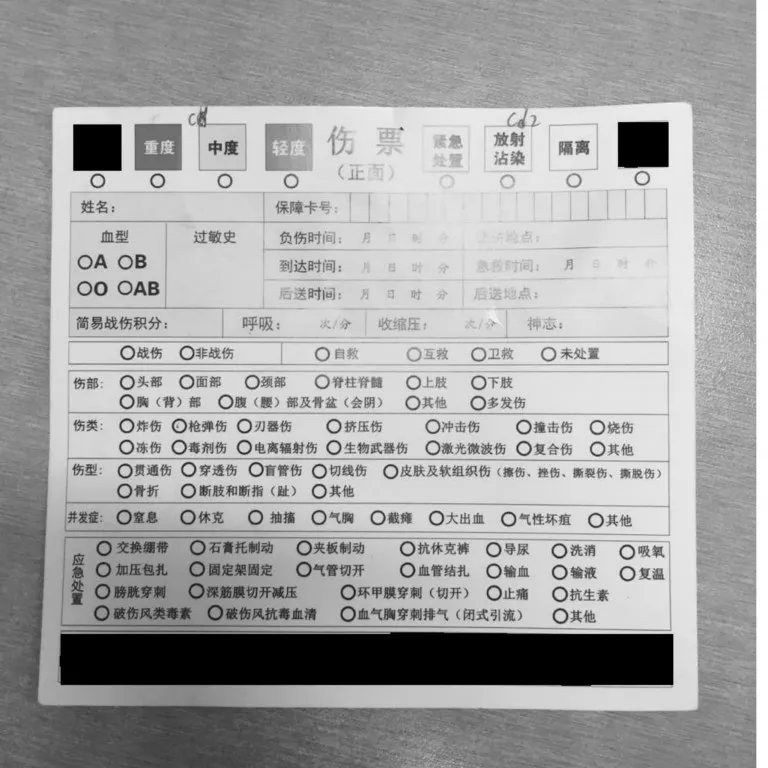
图6 伤票标记区域提取效果图

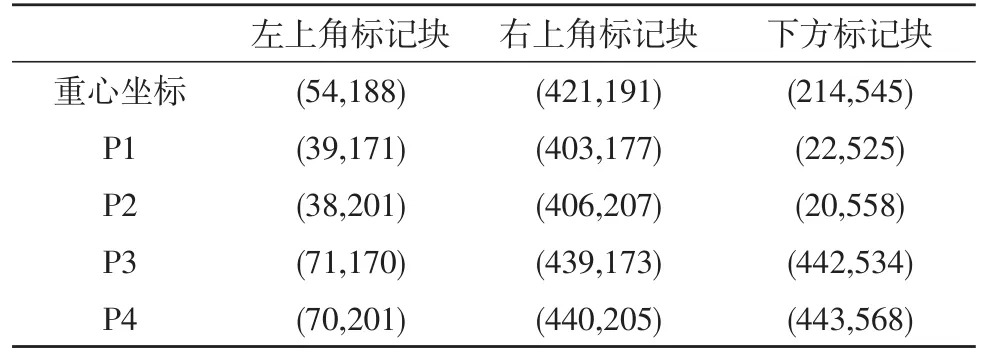
表4 标记区域提取信息表

参考文献:

[1]张树华.战时卫生勤务学[M].北京：解放军出版社，2006.

[2]师廷伟，金长江.基于FPGA的并行全比较排序算法[J].数字技术与应用，2013（10）:126-127.

[3]冈萨雷斯.数字图像处理[M].北京：电子工业出版社，2011.

[4]廖春生.基于数学形态学车牌定位算法仿真研究[J].计算机仿真，2011，28（12）:353-356.

[5]陈鑫元.自适应阈值图像二值化及形态学处理的FPGA实现[J].电子测量技术，2016，39（7）:68-71.

[6]刘紫燕，祁佳.实时图像边缘检测形态学优化设计及FPGA实现[J].计算机技术与应用，2013，39（9）:132-134.

[7]邓俊俊.基于内容的图像检索技术研究[D].南京:南京理工大学，2012.

[8]谢季峰.基于霍夫变换的划痕检测算法应用[J].电脑知识与技术，2012（20）:4957-4958，4961.

[9]张明慧，卢振泰，张娟.基于多图谱活动轮廓模型的脑部图像分割[J].计算机学报，2016:39（7）:1491-1500.

[10]SONG Xin-hang，JIANG Shu-qiang，Herranz L.Joint multifeature spatial context for scene recognition in the semantic manifold[C]//Proc of the IEEE Conf on Computer Vision and Pattern Recognition.Piscataway，NJ:IEEE，2015:1312-1320.

[11]胡永强，宋良图，张洁，等.基于稀疏表示的多特征融合害虫图像识别[J].模式识别与人工智能，2014，27（11）:985-992.

[12]刘紫燕，祁佳.实时图像边缘检测形态学优化设计及FPGA实现[J].计算机技术与应用，2013，39（9）:132-134.

[13]余江.基于轮廓的形状匹配方法研究[D].安徽:安徽大学，2013.

[14]王宇新.基于特征分布的图像识别方法研究与应用[D].大连：大连理工大学，2012.

[15]Krizhevsky A，Sutskever I，Hinton G E.ImageNet classification with deep convolutional neural networks[C]//Proc of the 26th Annual Conf on Neural Information Processing Systems.Cambridge，MA:MIT Press，2012:1097-1105.

[16]XIAO Jian-xiong，Hays J，Ehinger K，et al.Sun database:Large-scale scene recognition from abbeytozoo[C]//ProcoftheIEEE Confon Computer Vision and Pattern Recognition.Piscataway，NJ:IEEE，2015:3485-3492.