无线电能传输系统平行多匝线圈空间位置与效率分析

张晋勇，麦晓冬，关曼清，邱怡怡

（广东轻工职业技术学院信息技术学院，广东广州510300）

磁感应耦合式无线充电技术的出现，实现了用电设备和供电电源之间电能的无接触传输，并广泛应用于各个实用领域，例如便携式无线充电器[1]、植入式医疗设备体外无线供能、新能源电动汽车无线充电等[2]。基于磁耦合谐振的无线电能传输是两个具有相同谐振频率的物体之间利用近场强耦合实现高效能量交换。该技术除了具有较大的传输距离的优势外，还具有较高的效率、功率，对人体没有伤害，良好的穿透性等特点[3]。因此，该技术已逐渐成为新的发展方向[4-5]。

目前国内外在电磁耦合谐振式无线电能传输方面的研究主要针对单负载接收线圈在与发射线圈同轴情况下的功率与效率问题[6-7]。而在实际使用情况中，很难实现两线圈始终保持同轴的情况。用户的使用随意性使得无线电能传输系统的功率与效率在接收线圈水平位置偏移情况下的变化规律分析与研究变得尤为重要。

文献[8]给出了两平行线圈互感的新表达式，但并没有对无线电能传输系统进行研究[8]；文献[9]给出了无线电能传输系统中串串式拓扑模型下功率和效率的计算方法[9]，但互感采用最基本的计算，无法对线圈错位下功率和效率进行测算。在两线圈同轴的能量传输方面，文献[10]利用中继线圈提高了无线电能传输系统的传输距离[10]；文献[11-12]利用耦合模原理研究了输电系统效率与距离、线圈的匝数、线圈半径的关系[11-12]；文献[13]实验研究了不同频率下，传输距离与传输效率的关系[13]。文献[14]仿真实现了97%的传输效率，并实现了10 kW的电能无线传输[14]。这些文章也主要研究单负载接收线圈在与发射线圈同轴情况下的功率与效率问题，并没有给出线圈空间错位对功率的影响分析。

文中基于电路模型，利用线圈的互感式解耦后建立了Bessel函数与Struve函数的无线充电系统功率与效率数学模型，并给出功率与效率随空间位置变化的计算方法，之后搭建实验平台验证该方法的准确性，为解决因水平错位导致的充电系统功率与效率下降问题提供了有利依据。

1 互感线圈解耦的无线充电系统功率、效率计算方法

1.1 “串串式”传输系统的功率、效率

现应用较多的无线电能传输系统的分析模型主要是电路模型理论。其主要是建立系统的物理模型，对各元件的参数等效后进行分析[15]。电路模型根据发射端与接收端不同的元件接法也有4种不同的模式，由于实验交流电压很小、选用负载阻抗较小，所以文中利用“串串式”模型[16]进行无线电能传输系统的分析。“串串式”电路模型如图1所示。

图1 “串串式”两线圈耦合等效电路模型

根据基尔霍夫定律，可列出图1所示电路模型的回路方程：

其中ω是系统的角频率，uin是电源电压，R1、R2分别是电感L1、L2的等效电阻。

Z1、Z2是发射线圈、接收线圈的阻抗，分别为：

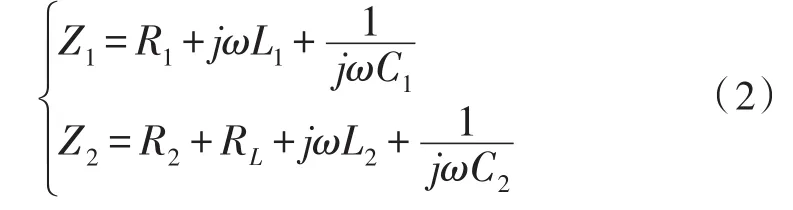
因此，整理公式（1）、（2），负载功率可化简为：

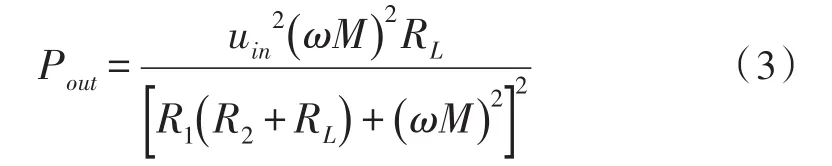
输出效率公式可化简为：

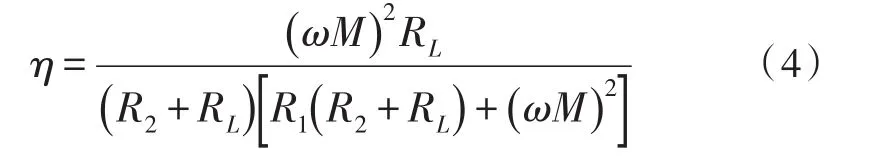
1.2 平行轴线圈解耦的互感计算

从公式（3）和公式（4）可以看出，无线电能传输系统的功率和效率主要取决于平行轴线圈之间的互感。为确定线圈空间位置与无线电能传输系统的功率与效率关系，互感利用平行轴线圈解耦方法计算。

两平行线圈，它们之间的互感为[17]：

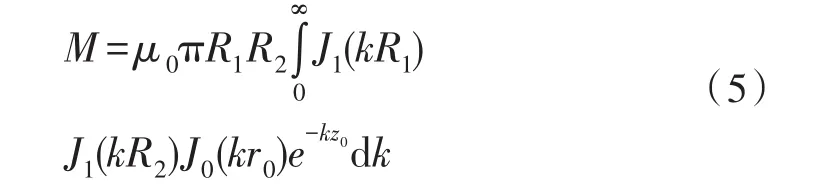
其中，R1、R2为圆环线圈的半径，z0为两平行线圈的轴向距离，r0为它们的轴间距离，μ0=4π×10-7H/m为真空磁导率。

无线电能传输系统所采用的线圈大部分是圆盘线圈，圆盘线圈的参数由图2所示。

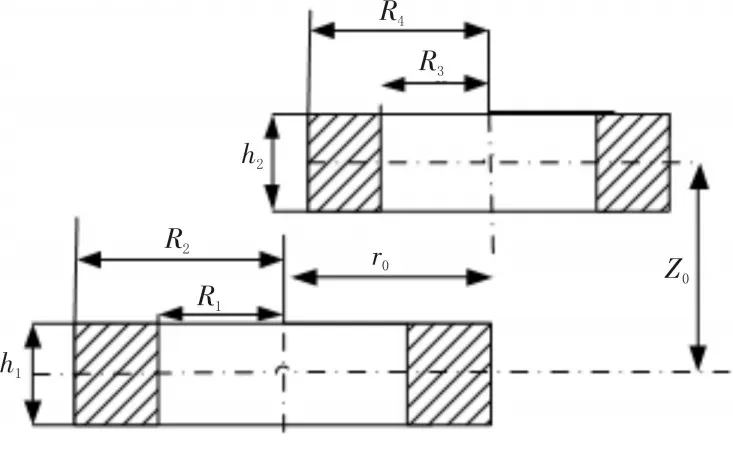
图2 平行线圈侧视图

根据圆盘线圈的特点，可视为h1=h2=0，按照图2所示参数，将式（5）运用倒数距离解耦展开即可得到：

1）对r0≥R2+R4

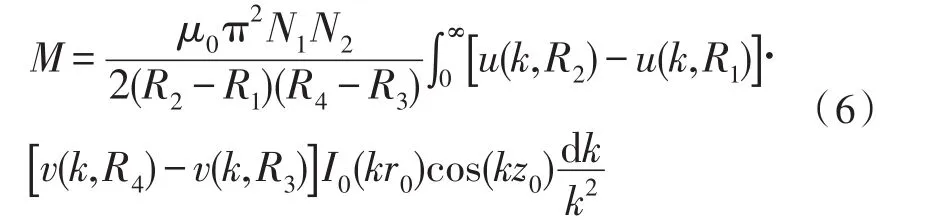
2）对 0≤r0≤R3-R2

3）r0无限制的线圈互感

式（6）～（8）是在两个平行的平面线圈的条件下得出的，即h1=h2=0，在此条件下，公式（6）～（8）中的主要参数如公式（9）～（11）所示。

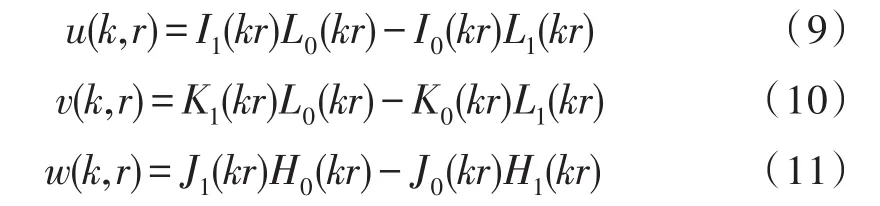
以上公式中所用到的特殊函数见表1所示。

表1 特殊函数汇总表

1.3 线圈平移位置与电能无线传输系统的效率关系

在Matlab中编程计算线圈平移距离与系统输出效率的变化规律。设定系统的谐振频率f在700 kHz左右，负载电阻50Ω，发射线圈与接收线圈的参数如表2所示。

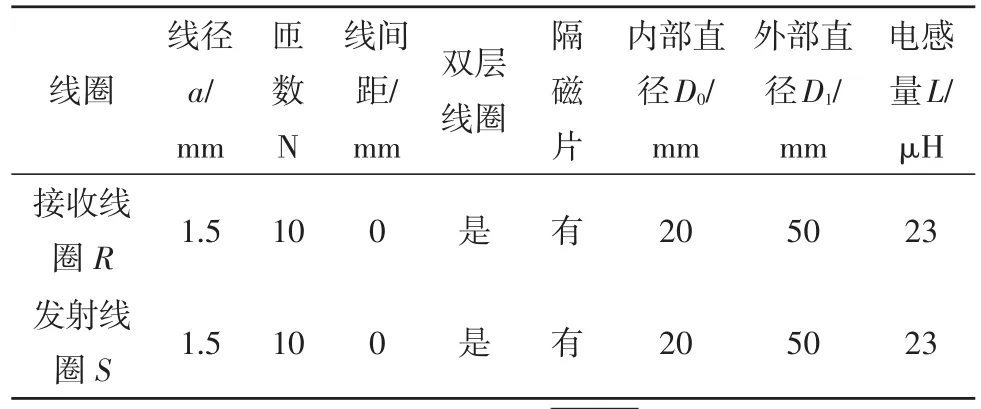
表2 线圈参数

为了得到线圈平移距离与系统传输效率之间的关系，先确定线圈的初始位置如图3所示。发射线圈为S，接收线圈为Re，设S内圈的圆心O的坐标为 (0，0，0)，Re 内圈的圆心的坐标为 (0，0，d)，且线圈S、Re所在的平面相互平行。

图3 两线圈的初始位置

根据据图1建立磁耦合谐振无线电能传输系统数学模型。为了达到谐振条件，分别串接C1=C2=2 nF的电容。

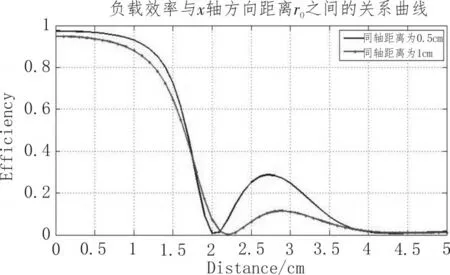
图4 线圈平移距离与系统传输效率的关系

在线圈间距离d=0.5mm和d=1mm的两种情况下，分别计算接收线圈的X轴移动距离与系统效率的关系曲线如图4所示。图4可以看出，在d=0.5mm时，同轴时系统效率最大，随着线圈平移距离的增大，系统效率下降较快；在d=1mm时，同轴时系统效率没有d=0.5mm时大，但随着线圈平移距离增大，系统效率下降较慢。

从以上分析可以看出，同轴效率高，平移过程中效率下降速率较大；同轴效率低，平移过程中效率下降速率较小。也即在选取系统最佳工作点时，根据用户使用区域进行同轴距离的选取，从而使效率在一定区域内的平均值最大。以上分析为使效率最佳的同轴距离d的选取提供了有利依据。

2 系统空间位置与效率关系实验验证

为了验证本文所提出的互感线圈解耦的无线电能传输系统的功率与效率计算方法的正确性，设计制作了一套线圈平移结构的磁耦合谐振无线电能传输系统。该系统由信号发生器（产生0～3 MHz方波信号），电源，MOSFET开关管BLF175为核心的功放电路，发射接收线圈，负载等组成，如图5所示。系统各参数如上仿真所述，固定负载电阻RL和同轴距离d，改变上层接收线圈的平移距离，验证平移距离与系统传输效率的变化规律。

实验时，利用一台示波器测量发射线圈电压，接入交流电流表，计算输入功率Pin=UI；同时利用另一台示波器测量负载电压，计算输出功率Pout=U2/RL。由此计算出系统的传输效率η。表3列出线圈间距分别为的0.5mm和1mm情况下实测输出功率与效率计算值。

图5 空间位置与效率关系实验验证

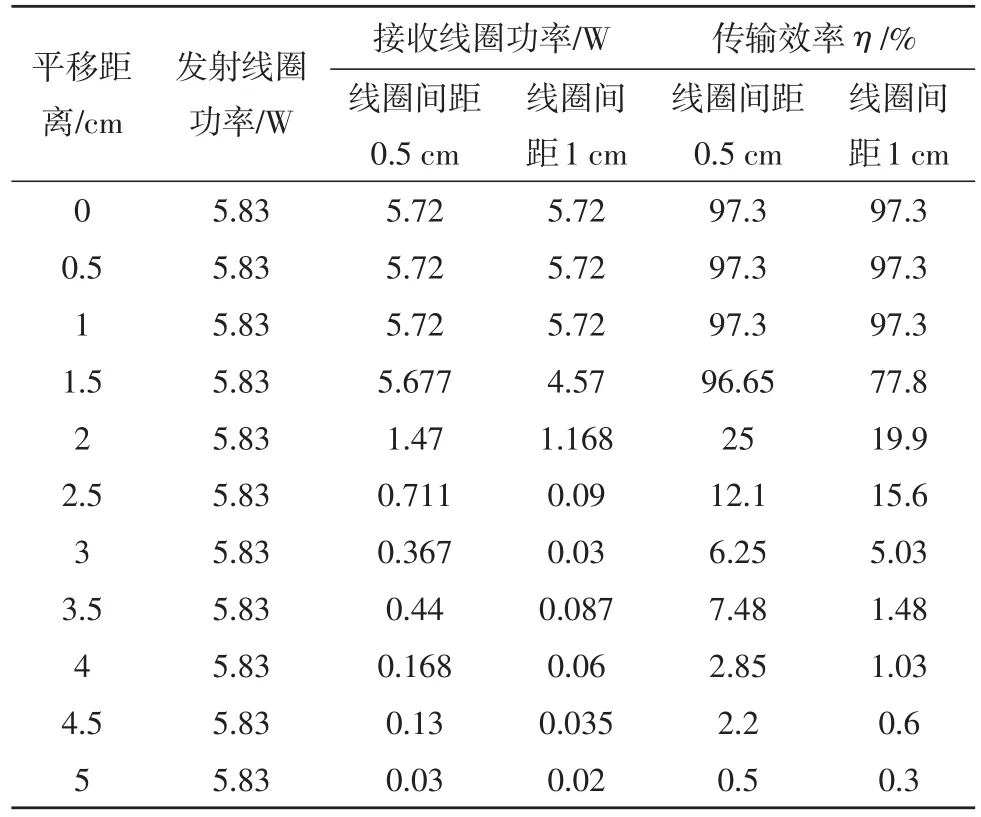
表3 线圈平移距离与接收线圈功率效率实验数据

从表3中的数据可以看出，线圈间距为0.5 cm时效率变化随着平移距离的变化速率较线圈间距为1 cm时的较慢。

实验数据与matlab仿真数据对比图如图6、图7所示。

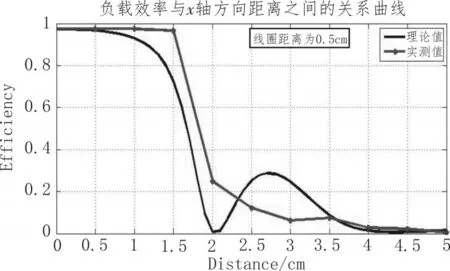
图6 线圈间距0.5 cm

实际传输效率随平移距离的曲线与仿真传输效率随平移距离的曲线误差在5%以内。实验结果验证了互感线圈解耦的无线充电系统功率与效率计算方法的正确性。

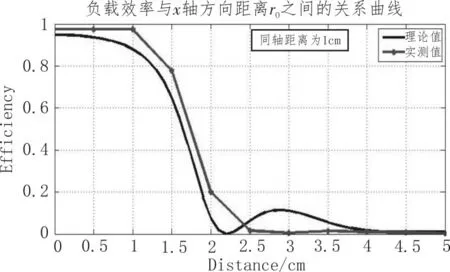
图7 线圈间距1 cm

实验数据与仿真数据存在一定差别：一方面由于所使用的线圈带有磁片，在仿真计算时可能存在误差；另一方面式（8）适用范围太广，在近距离情况下，互感计算也会存在一些误差。

3 结束语

1）针对负载线圈空间错位而导致的效率下降问题，提出了互感线圈解耦的无线充电系统功率、效率计算方法。根据互感线圈的解耦展开建立了基于变形Bessel函数与变形Struve函数的无线充电系统功率与效率数学模型，利用数值积分的方法计算了线圈空间位置与系统功率、效率的关系。

2）实际传输效率随平移距离的曲线与仿真传输效率随平移距离的曲线误差在5%以内。如果选用某一范围内的平均效率作为系统的评价指标，则该方法提供了有利依据。

参考文献：

[1]彭若晨，闫妍.无线功率传输的便携性设备应用[J].电子设计工程，2015，23（10）:83-85.

[2]Davide Bavastro，Aldo Canova，Vincenzo Cirimele，et al.Design of wireless power transmission for a charge while driving system[J].IEEE Transactions on Magnetics，2014，50（2）:965-968.

[3]刘野然，曾怡达.基于DE类功放的无线电能传输系统设计与分析[J].电子设计工程.2015，23（2）:98-101.

[4]赵争鸣，张艺明，陈凯楠.磁耦合谐振式无线电能传输技术新进展[J].中国电机工程学报，2013，33（3）:1-13.

[5]李博，朱宸綦，刘佳敏.基于磁谐振技术的无线充电装置[J].电子设计工程.2016，24（10）:111-113.

[6]Seung-Hwan Lee，Robert D.Lorenz.Development and validation of model for 95%-efficiency 220-W wireless power transfer over a 30-cm air gap[J].IEEE Transactionson Industry Applications，2011，47（6）:2495-2504.

[7]李阳，杨庆新，闫卓，等.无线电能有效传输距离及其影响因素分析[J].电工技术学报，2013，28（1）:106⁃112.

[8]罗垚.平行轴圆柱线圈互感计算的新方法[J].电工技术学报，2016，31（2）:31-37.

[9]刘志峰，刘瑞，黄海鸿，等.磁耦合谐振串串式无线电能传输研究[J].现代电子技术，2015，38（17）:127-132.

[10]ZHANG Fei，Hackworth S A，FU Wei-nong，et al.The relay effect on wireless power transfer using witricity[C]//2010 the 14th IEEE Conference on Electromagnetic Field Computa⁃tion.:IEEE，2010：548⁃552.

[11]LI Yang，YANG Qing-xin，CHEN Hai-yan，et al.Basic study on improving power of wireless power transfervia magnetic resonance coupling [J].Advanced Materials Research，2012，459（1）:445⁃449.

[12]Yang Li，Qingxin Yang，Haiyan Chen，et al.Basicstudy on improving power of wireless power transfervia magnetic resonance coupling[J].AdvancedMaterialsResearch，2012（459）:445-449.

[13]Chunbo Zhu，Kai Liu.Simulation and experiment alanalysis on wireless energy transferbased onmagnetic resonances[C]//IEEE Vehicle Power and Propulsion Conference，China，2008:1-4.

[14]Yu X，Sandhu S，Beiker S，et al.Wireless energy transfer with the presence of metallic planes[J].Applied physics letter，2011，99（21）:1230-610.

[15]Fei Zhang，Steven A Hackworth，Weinong Fu，et al.The relay effect on wireless power transfer using⁃witricity[C]//The 14th Biennial IEEE Conference onElectromagnetic Field Computation，2010:1.

[16]Linhui Chen，Shuo Liu，Yong Chun Zhou.An optimizable circuit structure for high-efficiency wireless power transfer[J].IEEE Transactions on Industrial Electronics，2013，66（1）:339⁃349.

[17]Conway J T.Inductance calculations for circular coilsof rectangular cross section and parallel axes using Besseland Struve functions[J].IEEE Transactions on Magnetics，2010，46（1）:75-81.