销轴孔过盈配合的弹簧质子模型研究

郑淑丽

(长沙职业技术学院 机械与汽车分院，湖南　长沙　410217)

0　引言

销轴与孔过盈配合由于结构简单、承载能力大和良好的对中性在工程中得到了广泛的应用。然而销轴与孔过盈配合经常在实际工作中出现结构性损伤，严重影响了其使用性[1-2]。现代机械制造中为了提高效率、制造精度和承载能力，要求大量采用销轴与孔过盈配合连接。据统计销轴孔连接部位是机械中最薄弱的地方，约60%～80%的机械疲劳现象出现在连接处[3]。

销轴与孔过盈配合引起连接处接触界面出现不规则的应力分布，并且边缘处出现应力集中。范小秦等[4]利用数学解析法推导了接触界面的应力和位移，并分析了应力集中产生的原因，为结构设计提出了参考意见。多国学者对销轴与孔之间的过盈配合影响参数(如不同的过盈量、摩擦因数、载荷等)进行了有限元仿真分析研究[5]，得到了各种影响参数的变化规律，但没有进行定量分析。销轴与孔之间的过盈配合属于非线性接触，计算非线性接触问题有许多方法，如罚函数法、拉格朗日乘子法等，这些方法与实际结构结合不紧密，影响了在工程中的应用[6]。

本文研究销轴与孔过盈配合产生的应力分布状态，从力学等效的角度将销轴与孔过盈配合转换为等价弹簧质子模型，对弹簧质子模型进行力学分析。

1　问题描述

设有一销轴直径为d0，一方板内有直径为D0的孔，将销轴插入方板孔，由于销轴直径d0大于孔直径D0，所以形成过盈配合。在配合过程中销轴受压缩应力缩小，孔受压缩应力张开，最后直径都变为D。图1为销轴与孔过盈配合示意图。

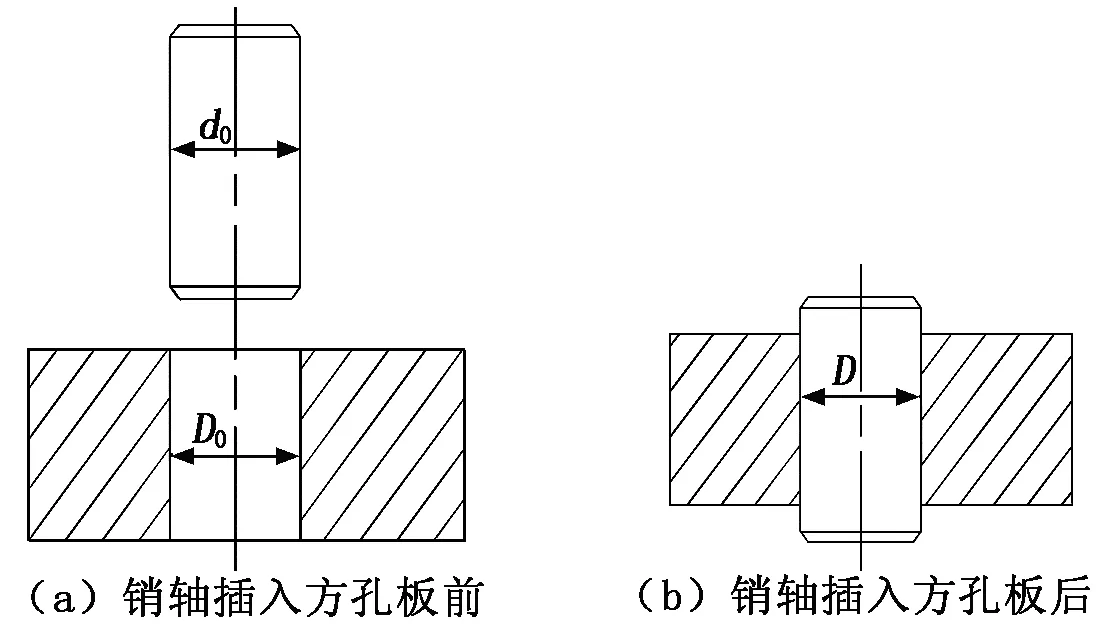
图1　销轴与孔过盈配合示意图

为了模拟实际工况，固定销轴两端没有与孔接触的部分，然后在板的一个侧面施加拉伸载荷F，模拟销轴与孔过盈配合承受外载荷。方板的应力如图2所示。

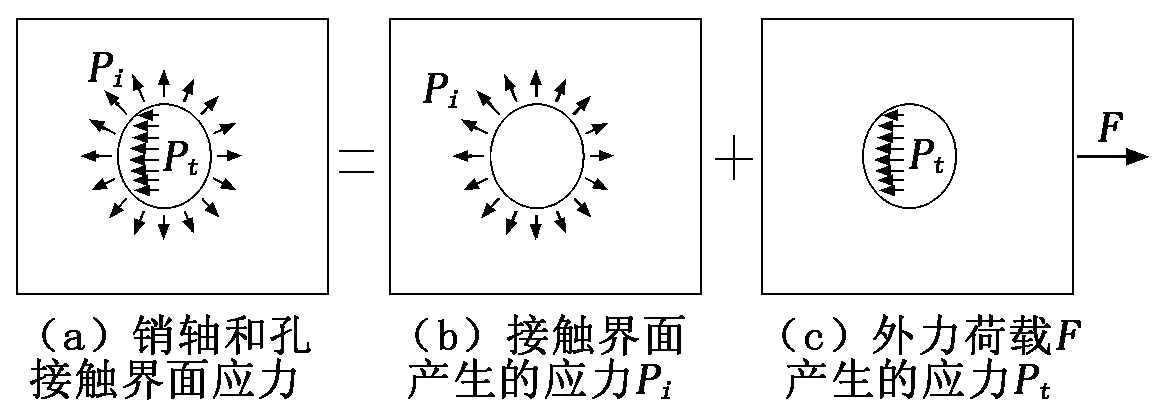
图2　销轴插入孔后及承受负载F时应力分布示意图

销轴和孔接触界面应力可以分成两个部分，一部分是由于销轴与孔过盈配合使销轴和孔接触界面产生的应力Pi，另一部分是由于外载荷F的施加使销轴和孔接触界面产生的应力Pt。在这两个应力作用下，销轴和板上在销轴和孔过盈配合接触界面附近应力变化较大，随着与接触界面距离的增大应力变化趋于平缓。

根据圣维南原理，在板上总可以找到一个圆，圆外应力分布与销轴与孔过盈配合产生的应力无关，与外载荷产生的局部应力无关，只与宏观外载荷有关，将这个圆定义为圣维南边界圆。销轴与孔加载情况如图3所示。

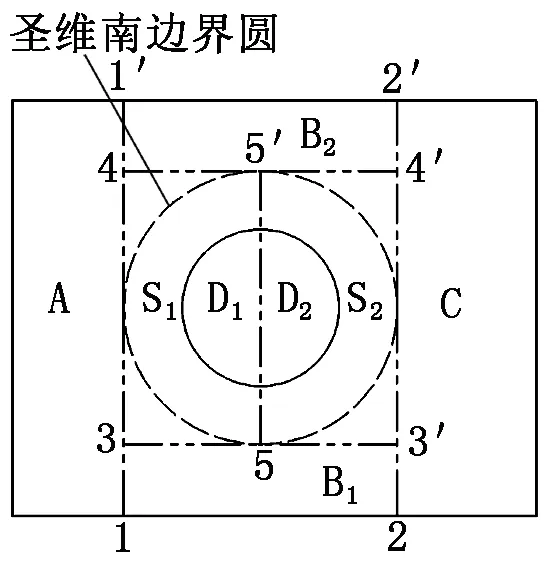
图3　销轴与孔加载情况

在板上做圣维南边界圆的两条竖直切线1-1′和2-2′，然后画两条水平切线3-3′和4-4′，以销轴圆心为中心画一条竖直分割线5-5′，这样销轴和平板面被5条分割线分割成D1、D2、S1、S2、B1、B2、A、C几个部分。

2　弹簧模型

为了简化分析，假设：①所有销轴和平板的变形均属于弹性变形；②板上受销轴挤压发生的全部变形集中在S1、S2上，其他部分只发生拉伸成压缩变形；③忽略板的几何形状和尺寸(如边距)对销轴径向变形的影响，销轴沿径向均匀压缩，孔壁在厚度方向上与销钉形成均匀的干涉；④销轴与孔过盈量和外载F足够小，在初始状态及施加外载之后，结构不发生开裂且只发生弹性变形。

由于认为结构只发生弹性变形，忽略整个结构中的塑性变形，因此可采用具有同等刚度的弹簧代替相应结构进行建模，将销轴和板的质量转换为质子。

销轴在初始状态下处于压缩状态，施加外载F后，其D1部分被进一步压缩。当F较小时，D2的压缩变形仅被部分释放；当F超过一定值时，D2的变形完全释放，D2与孔间形成间隙。因此，销轴可被看作是由两个刚度相等的弹簧D1和弹簧D2以及质子D1和质子D2组成。

初始状态下，由于销轴对孔的膨胀作用，S1、S2沿纵向被压缩；施加外载F后，其压缩状态发生变化。由对称性知：S1与S2的刚度、变形及内力相等；B1和B2两块只发生压缩或拉伸，可以等效为弹簧，且两弹簧刚度和变形量相等，因此，由两个完全一样的弹簧B1和B2并联成一个弹簧B，设B的等效刚度为KB。由于A、C模块处于弹性变形，对销轴与孔接触界面没有影响，故不考虑A、C对整个模型的影响，将其作为一个整体质量。

综上所述，建立销轴与孔过盈配合的弹簧质子模型如图4所示，其中M表示图3对应部分的等效质量，K为对应部分的等效刚度。由于销轴与孔之间是接触界面没有刚性连接，因此建立的弹簧质子模型中质子S1与质子D1及质子S2与质子D2之间是刚体接触，只传递压力，不能传递拉力。O点为固定约束点。

3　模型受力分析

设在初始状态下，弹簧D1、D2具有相同的初始压缩变形，当外载荷F=0，平衡时，xD1=xS1、xD2=xS2，则弹簧质量模型的受力方程为：

(1)

其中：FD1-S1、FD2-S2分别为质子D1和S1及质子D2和S2之间的接触压力；KD1、KD2分别为弹簧D1、D2的刚度；KS1、KS2分别为弹簧S1、S2的刚度；xD1、xD2分别为质子D1、D2的位移量；xS1、xS2分别为质子S1、S2的位移量；xA、xC分别为两侧板的位移量。

当有外载荷F≠0，平衡时，xD1≠xS1、xD2≠xS2，则弹簧质量模型的受力方程为：

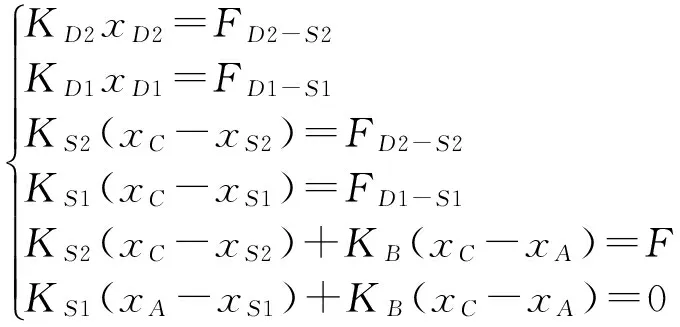
(2)

随着F从0逐渐增大，左侧弹簧D1和S1逐渐被压缩，右侧弹簧S2和D2被压缩量逐渐减小；当载荷F增加到一定数值时，弹簧D2和S2的被压缩量减小为0，质子D2和S2之间没有弹簧压缩量形成的接触压力；当载荷F继续增大，弹簧D2和S2不发生变形，质子D2和S2将发生分离。设使销轴与孔分离时外载荷的值为F，实际工作过程中外载荷是交变载荷，故可设:

F=F1+Asin(ωt+φ).

其中：F1为外载荷基本值；A为外载荷的振动幅值；ω为外载荷的振动圆频率；φ为外载荷的振动初始相角。

(1)F1+A

(2)F1-A>F0：最小的外载荷大于使销轴和孔分离的外载荷。在动载荷加载的过程中，销轴和孔接触界面始终有部分分离。由于销轴和孔接触界面发生分离和接触交替状态，造成界面之间发生频繁撞击，会造成表面的机械损伤，影响结构寿命。

(3)F1-A

4　结论

根据销轴与孔的过盈配合，建立过盈配合的弹簧质子模型，分析受力状态，得到如下结论：

(1) 当外载荷较小不足以引起销轴和孔过盈配合接触界面发生分离时，由于销轴的变形使板受到的载荷变化幅度小于外载荷变化幅度，可以使结构疲劳寿命延长。

(2) 当外载荷能使销轴和孔过盈配合接触界面发生分离时，由于接触界面的分离和接触交替进行，使界面承受反复撞击，会造成界面的机械损伤和微动疲劳。

(3) 为了延长过盈配合结构的寿命，应根据结构承受的外载荷量确定销轴与孔过盈量。

参考文献：

[1]周玉华.VOLVO A40E铰卡铰接销孔配合失效故障分析及处理[J].铜业工程，2015(2)：92-96.

[2]胡慧玲，林楚新.某活塞销的断裂失效分析[J].热加工工艺，2015(24):226-228.

[3]Croccolo D,Agostinis M D,Ceschini I，et al.Interference fit effect on improving fatigue life of a holed single plate[J].Fatigue and Fracture of Engineering Materials and Structures,2013，36(7):689-698.

[4]范小秦，孙丽萍，王玉艳，等.轴孔过盈配合的解析解[J].机械,2011,38(9):26-30,43.

[5]Chakherlou T N,Abazadeh B.Investigating clamping force variations in A12024-T3 interference fitted bolted joints under static and cyclic loading [J].Materials and Design,2012,37:128-136.

[6]李梅竹.基于ANSYS等距型面轴孔配合特性的研究[J].机械制造与自动化,2016(2)：134-142.

[7]张岐良，曹增强，甘学东，等.拉伸板中心孔干涉配合对载荷幅值的影响[J].航空学报，2014，35(6)：1643-1650．

[8]周仲荣.关于微动磨损与微动疲劳的研究[J].中国机械工程, 2000,11(10):1146-1150.