一种新型副镜调整机构的位姿误差分析与测试研究∗

叶 宇 乐中宇 顾伯忠

(1中国科学院国家天文台南京天文光学技术研究所南京210042)

(2中国科学院南京天文光学技术研究所天文光学技术重点实验室南京210042)

(3中国科学院大学北京100049)

1 引言

在大口径光学红外望远镜中,主副镜之间的相对位姿对望远镜的成像质量起着至关重要的影响.随着望远镜新技术的发展,望远镜结构尺寸越来越大,提高结构刚度已难以满足镜面位置定位精度的要求.由于主镜尺寸结构庞大,调整主镜的相对位置较为困难,所以研究副镜调整机构对改善望远镜的成像质量有着特别重要的意义.

近几年国内外建成的天文望远镜上大都使用六杆机构作为副镜调整机构,例如,10.4m GTC[1](Gran Telescopio Canarias)、8m VLT[2](Very Large Telescope)、4m VISTA[3](Visible and Infrared Survey Telescope for Astronomy)以及国内上海的65m射电望远镜,成都光机所的1.8m望远镜,中国SONG计划项目望远镜以及西安光机所和长春光机所都设计了各自的副镜调整机构.长期以来,研究人员一直致力于提高望远镜副镜调整机构的定位精度,Schipani研究了6-6 Stewart平台的运动学像差控制[4],徐刚等人提出了基于Gough-Stewart平台的副镜位姿精调机构的运动精度准则和刚度准则[5],韩春杨等人设计了一种用于大型光学载荷副镜在轨位姿精密调整的Hexapod型平台[6].这些文献大多通过优化结构参数,减小上下铰链间隙误差等方法来提高位姿精度,都是从设计分析平台结构的角度来考虑,而很少有通过实际测试来分析影响平台精度的因素.

国内外研究的用于副镜调整的机构大都采用传统的Stewart结构,这种结构及驱动特点会造成其径向载荷远小于轴向载荷,由于杆长的变化会造成运动过程中杆件刚度的变化,因此将会引入误差.天文望远镜副镜在空间不同角度位置工作,承受同等径向和轴向载荷,需要稳定的结构刚度,采用传统并联机构作为天文望远镜副镜调整机构,往往需要采用大结构尺寸来提高径向载荷和结构刚度.针对传统Stewart结构的缺点,提出了一种新型固定杆长杆端轴向平移运动模式的六杆机构,本文作者已经对该样机进行了理论模型分析,开展了动静力学研究,优化节点运动方向,优化连杆倾角,平衡径向与轴向载荷等工作[7].本文主要是在介绍这种结构样机的基础上,分析其运动特性,建立误差模型,讨论误差的主要来源,并通过搭建多自由度位姿检测平台对该机构进行了测试.

2 结构及运行特性

2.1 副镜调整机构结构

传统式Stewart平台,由6根可伸缩式杆件通过球铰、球销铰、虎克铰或其他特别设计的联接副与动平台和定平台相联,组成刚度很高的框架结构.而这种新型结构杆定长滑块移动式六杆机构则通过改变杆件一端节点的空间位置来实现动平台的6维空间运动,结构如图1所示:该机构主要由动平台、定平台和链接两平台的6根支链组成,每根支链通过连接杆链接在动平台上的动球铰和可在导轨上移动的定球铰,通过控制导轨上各个滑块的位置来实现动平台位姿的变化,使动平台能够完成1维调焦、两维平移、两维倾斜5个自由度的运动(在望远镜副镜调整中一般不考虑滚动角的变化).

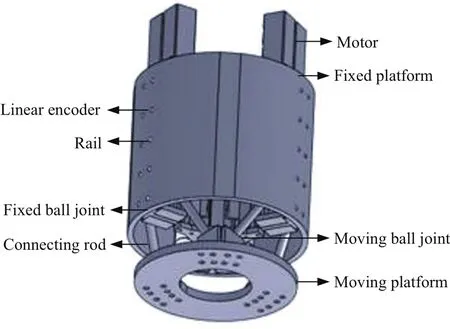
图1 副镜调整机构Fig.1 The adjustment mechanism of secondary mirror

传统方案利用较小的定平台就可以得到较大的动平台运动空间,但移动副直接承受动平台的载荷,要求驱动力较大、热量不易分散、杆长变化以后系统刚度和振动特性变化可能较大.新型方案相对于传统六杆机构,具有以下优点:可以获得比较接近的径向和轴向承载能力;可以利用较小的结构获得大的载荷;可以大大缩短轴向结构尺寸,减小镜筒长度;驱动部件始终在同一径向平面内,易于布置及固定;驱动部件可以选用高精度直线驱动单元,而且驱动部件可布置在定平台上从而可使发热量和振动的影响减少;结构刚性及振动特性更加稳定.这些优点正是天文望远镜副镜调整机构所需要的.缺点是动平台的各维运动行程相对较小,如果要加大行程,其径向尺寸会大大增加,对于天文望远镜副镜调整机构来讲,所需的运动行程很短,因此这个缺点并不造成影响.

2.2 运动模式

此六杆机构的平移驱动机构和位置传感器沿轴向布置,在望远镜中进行副镜支撑时能充分利用现有驱动结构从而降低成本,紧凑的结构减少了径向挡光.六杆机构运动空间的解算采用逆解法进行,即由动平台的目标位姿逆推杆移动端所需的位移.推导过程如下:在定平台中心固联全局参考系XY Z,在动平台中心固联局部坐标系X′Y′Z′,如图2所示,将动平台的位姿分解为局部坐标系原点在全局参考系的空间位置O′(x,y,z)与以初始姿态为基准的局部坐标系姿态(由进动角α、章动角β、自转角γ等3个欧拉角表示),动平台6个球铰的当前坐标根据动平台的当前位置和姿态来计算.下面是由动平台的局部坐标系向全局坐标系的姿态变换矩阵R:

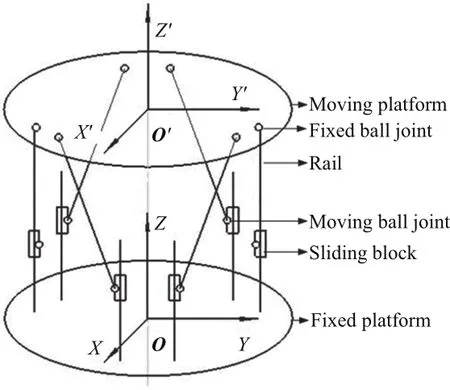
图2 固定杆长杆端轴向平移运动模式Fig.2 The axial translational motion model of the fixed length rod end

6个滑块目标位置求解过程:将动平台6个球铰在局部坐标系中的坐标向量(x′,y′,z′)T右乘姿态变换矩阵R即可得到其全局姿态向量(xZ,yZ,zZ)T,再加上局部坐标系原点在全局参考系的空间位置向量O′(x,y,z)T,可以得到球铰的全局位置向量(x,y,z)T,再根据六杆机构的杆长不变特点和空间两点距离公式列出方程,并已知对应导轨的直线方程,联立求解这6个方程,同时结合滑块的初始位置,即可求解出滑块球铰的目标位置.

2.3 结构样机

设计六杆机构的基本技术要求如表1所示.

设计实验样机的实际结构参数如下:平台重量20kg,平台最大外径300mm,动平台半径100mm,动球铰夹角20◦,平台高度87mm,定平台半径120mm,定球铰夹角43◦,杆长105mm.约定以动平台球铰分布圆的中心为系统坐标系的原点.动平台上的球铰编号为:A、B、C、D、E、F,如图3所示,各球铰的初始位置如表2所示.

表1 六杆机构技术指标Table 1 Hexapod technical requirements

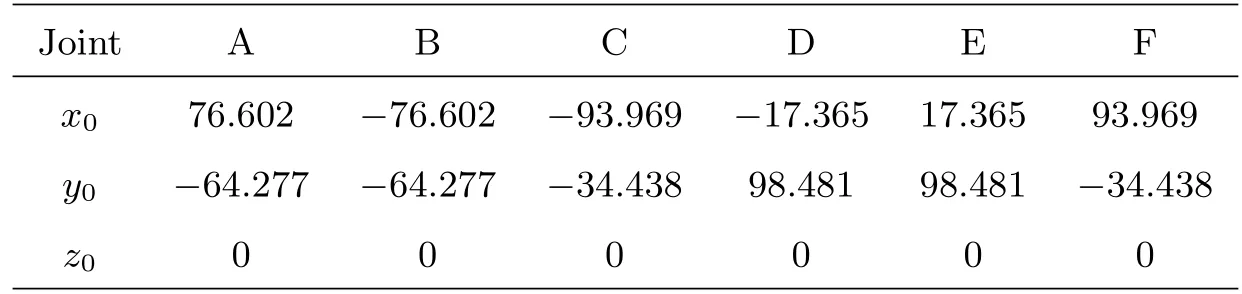
表2 动平台各球铰的初始位置(单位:mm)Table 2 The initial position of each ball joint of the moving platform(unit:mm)

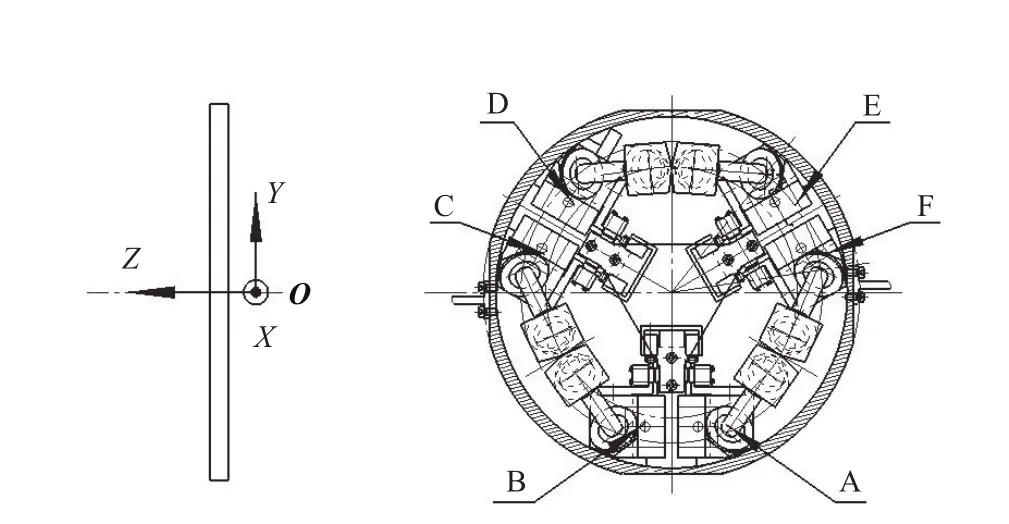
图3 实验样机结构Fig.3 The structure of experimental prototype

3 误差模型与分析

3.1 六杆机构误差模型

影响望远镜副镜位姿精度的因素除了六杆机构本身的结构以外,还包括主副镜之间温度梯度的变化和望远镜高度角引起的变化量.为了分析六杆机构结构误差,采用矩阵微分法对系统建立误差模型,单个连接杆矢量图如图4所示.第i根连接杆的封闭矢量环表示为:

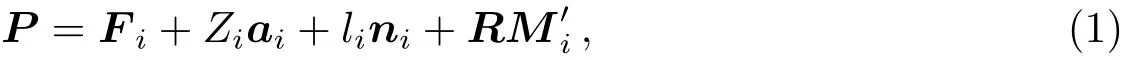
其中,O—定平台坐标系原点;O′—动平台坐标系原点;P—定平台坐标系原点到动平台坐标系原点的矢量;Fi—滑块初始位置矢量;Hi0—滑块初始位置;Hi—滑块运动之后的位置;Zi—滑块运动距离;ai—滑块运动方向单位矢量;li—连接杆长度;ni—连接杆方向单位矢量;—动平台坐标系下球铰Mi到O′的矢量.

图4 单个连接杆矢量图Fig.4 The vector diagram of one connecting rod

对上式进行全微分计算,可以得到动平台位姿误差模型:

转换矩阵的微分形式可表示为:

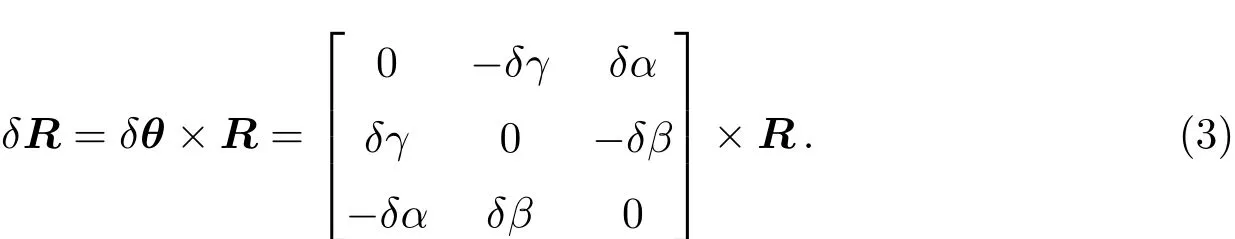
同时,Mi为动平台球铰在固定坐标系中的坐标矢量:

把(3)–(4)式代入(2)式可得:

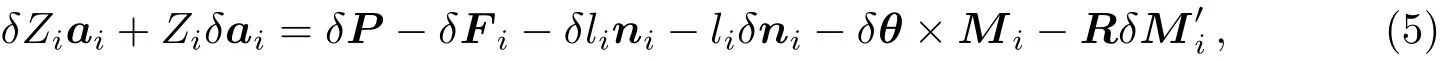
同时考虑6根连接杆可得:

其中,

上述公式中,δX为动平台末端位姿误差矢量,δ∆X、δ∆Y、δ∆Z、δ∆α、δ∆β、δ∆γ分别为解算到动平台末端6个自由度位姿的误差矢量;δΛ为滑块运动矢量;δL为连接杆长度误差;δM′为动球铰位置误差;δH为定球铰位置误差;δA为导轨直线度误差.

由于六杆机构在工作空间内应避免位形的奇异性,故K可逆,则动平台运动误差模型为:

其中,总误差传递矩阵:E=K[I M N1N2N2]∈R6×66,I∈R6×6为单位矩阵,δε =[δΛTδLTδM′TδHTδAT]T∈ R66×1.

3.2 六杆机构误差分析

从误差模型可知,影响副镜调整机构的因素主要有:滑块运动误差、连接杆长度误差、动球铰位置误差、定球铰位置误差和导轨直线度等.从方程(8)可以看出,方程含有1维滑块移动误差、1维连接杆长度误差、3维动球铰位置误差、3维定球铰位置误差和3维导轨直线度误差共11个未知量,6根连接杆总共有66个未知量,测量标定较为困难.动球铰和定球铰的位置误差主要受球铰的间隙和弹性形变等因素的影响,由于此六杆机构的球铰在整个工作空间内运动范围很小以及负载较轻,可以认为球铰位置误差变化量是一个小量[8].由于系统所设计的结构为杆定长结构,通过对虚拟样机模型分析,当高度角从0◦变化到90◦范围时,引起动平台平移的变化量为0.5–0.28µm,故认为杆长误差变化量很小,可以忽略,如图5显示了高度角0◦和90◦时引起动平台平移的位移量.

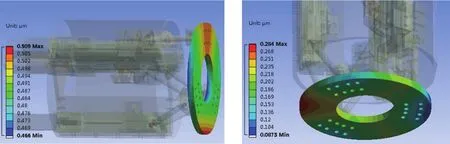
图5 不同高度角下杆长引起动平台的位移量(左图:高度角0◦;右图:高度角90◦)Fig.5 The displacement of the moving platform caused by the length of the rod at different altitudinal angles(left:0◦;right:90◦)

由定杆长滑块移动式六杆机构的特点可知,所有传动链上的误差最终都传递到滑块上,所以主要考虑滑块运动误差和导轨直线度对六杆机构运行精度的影响.滑块运动误差主要受驱动控制系统精度的影响,控制系统的精度由反馈元件的定位精度所决定,本系统采用海德汉直线光栅尺作为位置反馈元件,重复定位精度±2µm,分辨率0.1µm.6根运行导轨选用THK公司的球保持型智能组合单元SKR26,导轨重复定位精度约为3µm,直线度约为10µm.当滑块在导轨上沿z轴方向运动时,如图6(a)所示,导轨的运动被限制了5个自由度,即沿x轴、y轴的移动自由度和绕3个轴的旋转自由度,只保留沿z轴方向的移动自由度.由于受导轨制造误差、安装基准面误差、导轨直线度等综合因素的影响,滑块实际运行过程中会在上述5个自由度上产生额外的运动,这就是滑块运动误差,它主要分为运动角误差∆α(x)、∆β(x)、∆γ(x)和运动直线度误差∆x、∆y[9].∆α(x)和∆β(x)可以通过阿贝臂产生阿贝读数误差,∆γ(x)由于阿贝臂为零,故不会产生阿贝误差,但会微量改变光栅读数头和光栅尺的相对位置,由于光栅尺刻线有一定的宽度,所以不会影响正常读数,同时它对滑块在x轴上的偏离∆x也有一定影响,运动直线度误差∆x和∆y会直接改变球铰的空间位置,不仅会带来平移误差,而且还会带来角度误差,直接影响测量精度.

导轨直线度引起的误差如图6(b)所示.H为滑块的初始中心位置,L为固定杆长初始位置,H′和L′分别为导轨直线度引起变化之后的滑块位置和杆长位置,ϕ为固定杆长与动平台平面的夹角,b为H到X′的距离,c为H到H′的距离,d为H到Z′的距离.根据六杆机构优化设计值可知ϕ=43◦,并且在整个运行范围内变化很小,由于杆长|L|≫c,并且认为L保持不变,所以导轨直线度引起的变化量在Z轴上的分量为:

根据选择使用的导轨可知,b≈±5µm,则d≈±2.5µm.

图6 (a)导轨自由度示意图;(b)导轨直线度引起的误差Fig.6 (a)Schematic diagram of the freedom of the rail;(b)The error caused by the straightness of the rail

为了评估每根运动杆件对各个姿态运动的权重大小,通过实验标定得出了系统的位姿传递矩阵.标定过程如下:实验样机动平台的上表面呈竖直方向放置,标定测试1将4个千分表的探头打在动平台的上表面,如图7(a)所示.标定测试2将4个千分表的探头打在动平台的圆柱侧表面,如图7(b)所示.标定时让单个电机运动1mm,记录运动前后各个千分表的读数,计算探头相对运动量,按照电机顺序反复进行上述步骤,记录所有电机单独运动时千分表显示的相对运动量.对标定测试1处理数据,可以得到绕x轴和绕y轴的转动量和沿z轴的平移量,对标定测试2处理数据,可以得到沿x轴和沿y轴的平移量.沿x方向位移量为(Q′4− Q′2)/2,沿y方向位移量为(Q′1− Q′3)/2,沿Z方向位移量为(Q1+Q2+Q3+Q4)/4,绕x轴旋转为arcsin[(Q1−Q3)/T],绕y轴旋转为arcsin[(Q2− Q4)/T′],其中T是Q1到Q3的距离,T′是Q2到Q4的距离,Q1、Q2、Q3、Q4为标定测试1各个千分表的读数,Q′1、Q′2、Q′3、Q′4为标定测试2各个千分表的读数.

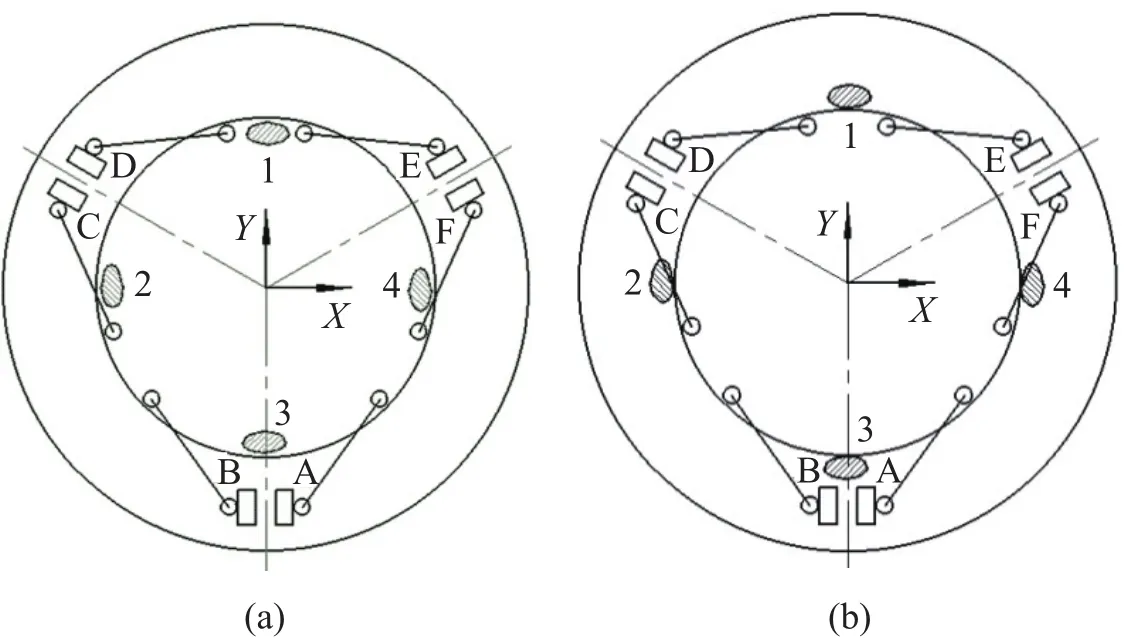
图7 (a)标定测试1;(b)标定测试2Fig.7 (a)Calibration test 1;(b)Calibration test 2

通过标定可以得到如下矩阵:

该矩阵是5行6列矩阵,表示当A、B、C、D、E、F 6个球铰所对应的电机分别运行1mm(由直线光栅尺读出)所引起x轴、y轴、z轴、绕x轴旋转和绕y轴旋转的变化量.从矩阵中可以看出,单个电机运动1mm,平移轴运动的最大值为510µm,旋转轴运动的最大值为0.2113◦,转换为角秒为760′′,由于导轨的直线度约为10µm,如果定义正负方向则为±5µm,根据平移轴和旋转轴运动的最大值,可以确定导轨直线度引起的平移轴最大变化量约为±2.5µm,旋转轴最大变化量约为±3.8′′,这跟理论推导的值极为接近,从而验证了该副镜调整机构误差主要是由导轨直线度所引起的滑块运动误差.

4 测试实验与方法

为了测试该六杆机构样机的运行精度,该副镜调整机构被安装到了一台望远镜上,通过搭建多自由度同时测量平台对该机构进行了位姿检测,如图8所示.

对于望远镜副镜调整机构而言,常用的位姿检测方法主要有[10]:机械接触式测量法、光干涉测量法、基于光敏元器件的测量方法、视觉测试法等.结合各种检测方法的优缺点,我们提出一种基于光纤准直技术的多自由度误差同时测量方法,采用光纤准直器作为光源,分别以角锥棱镜和分光直角棱镜作为3维平移误差和2维旋转误差的敏感器件,使光斑成像于CCD面板上,光纤光斑的中心代表了光线在空间的位置,光纤光斑中心的检测决定了测量的精度,通过测量光斑的位移量可以得到副镜动平台5个自由度的变化量.为了提高光斑中心的定位精度,引入了亚像素的定位方法,采用MATLAB图像处理可以使定位精度达到亚像素级别.

4.1 3维平移测量原理

平移误差的测量是以角棱锥镜作为敏感元件,原理如图9(a)所示.光纤点光源经准直器入射到沿副镜移动的角锥棱镜,经其反向返回后,由CCD相机接收.当角锥棱镜沿副镜动平台X轴方向平移∆x,经其反向返回的光斑将在CCD面板上平移的位移量为2∆x,通过该方法可以提高系统两倍的测试分辨率,Y轴、Z轴平移同X轴平移类似.

4.2 2维旋转测量原理

2维旋转角的测量是以分光直角棱镜为敏感元件,测试原理图如图9(b)所示.光纤准直光束通过半透半反镜入射到平面反射镜上,经其反射返回,通过半透半反镜,经聚焦透镜后,在CCD面板上成像.当副镜动平台绕X轴旋转θx(绕Y轴旋转θy)角度时,经其反射的光束将发生2倍的角度偏转,经透镜聚焦于CCD上的像点发生相应的位移,有:

式中,f为透镜焦距,∆x、∆y分别为像点在CCD上X轴和Y轴方向的位移[11−12].

图9 (a)平移测量原理图;(b)旋转轴测量原理图Fig.9 (a)The principle diagram of the translation measurement;(b)The principle diagram of the rotation axis measurement

5 测试结果

5.1 检测装置精度测试

为了得到测试方法能够达到的测试精度,利用色散共焦位移计(分辨率0.1µm,精度0.2µm,量程1.2mm)对检测装置进行了定标,确定了比例尺(即一个像素对应的位移量),保持副镜动平台位姿不变,采用CCD连续拍照20次,检测点分布如图10所示,采用统计方法可以计算出CCD的测试精度好于0.5µm.根据3维平移测量原理可知,平移测试精度是CCD测试精度的一半,故平移测试精度好于0.25µm;根据2维旋转测量原理,如果取透镜焦距f=250mm,则旋转轴的测试精度好于0.2′′.

图10 精度测试下的检测点分布Fig.10 The testing point distribution under the precision test

5.2 重复定位精度测试

重复定位精度(定位发散度)即对调整平台进行多次定位测量,比较得到同一位移指令下的定位精度.重复测量的极差=最大值−最小值:δ=δmax−δmin,利用贝塞尔公式:

可以得到测量的标准差,即为重复定位精度.上式中,s为重复定位精度,n为样本的容量,一般需要大于7,该测试样本取10,yi为第i个测量数据,¯y为数据的平均值.

由于结构加工、控制算法、检测装置等误差的存在,各个自由度位姿的输出存在相互耦合,单一自由度的运动会产生其他自由度位姿的变化.图11显示了5维自由度中的1维运动的重复定位误差,并实时监测其他4维运动引起的变动量.

从图11(a)和11(b)中可以看出,动平台沿两个旋转轴转动的过程中,两个旋转轴的最大重复定位精度好于1.4′′,引起X、Y、Z 3轴最大变化量<4µm.从图11(c)、11(d)、11(e)中可以看出,动平台沿3个平移轴运动的过程中,3个平移轴的最大重复定位精度好于4.5µm,引起两个旋转轴最大变化量<3.4′′且最大变化量大多出现在平移轴运动行程的较大位移处,由于副镜调整机构平移调整的范围一般都比较小,可以满足实际望远镜观测的需要.

6 结论

针对传统副镜调整机构Stewart结构的缺点,提出了一种新型固定杆长杆端轴向平移式六杆机构.利用矩阵微分法建立了误差模型,分析了各个误差源对运行精度的影响,通过实测位姿传递矩阵,验证了导轨直线度引起的滑块运动误差是影响机构精度的主要因素.通过搭建多自由度检测平台对该六杆机构进行测试,测试结果显示并联平台位姿误差不是各个误差源的简单线性叠加,而是各个误差源不同程度的重叠和相消,该副镜调整机构除绕X轴旋转的跳动量稍大于设计指标,其他指标都能达到设计要求,可以用于1–2m级口径望远镜中.同时该副镜调整机构的定位精度还有提高空间,可以从零部件选型、运动学误差标定、采用网格划分等方面建立动态补偿算法来进一步提高定位的精度.

图11 重复定位误差测试结果:(a)绕X轴旋转(α)重复定位误差;(b)绕Y轴旋转(β)重复定位误差;(c)X轴平移重复定位误差;(d)Y轴平移重复定位误差;(e)Z轴平移重复定位误差Fig.11 The test results of the repositioning errors:(a)The repositioning error of rotating around X-axis(α);(b)The repositioning error of rotating around Y-axis(β);(c)The repositioning error of X-axis translation;(d)The repositioning error of Y-axis translation;(e)The repositioning error of Z-axis translation

[1]Casalta J M,Geijo E M,Zago L.SPIE,2004,5495:507

[2]Stanghellini S.SPIE,1998,3352:675

[3]Geijo E M,Casalta J M,Canchado M,et al.SPIE,2006,6273:627338

[4]Schipani P.Investigative Ophthalmology&Visual Science,2006,9:472

[5]徐刚,杨世模,龚雨兵.光学精密工程,2008,16:1181

[6]韩春杨,徐振邦,吴清文,等.光学精密工程,2016,24:1093

[7]Yue Z,Ye Y.SPIE,2014,9145:91452P

[8]汪劲松,白杰文,高猛,等.清华大学学报(自然科学版),2002,42:758

[9]胡鹏浩,张建坤,马晓庆,等.机械工程学报,2015,51:1

[10]于阳.大型空间望远镜次镜精密调整机构研究.北京:中国科学院大学,2016

[11]吕勇,冯其波,刘立双,等.红外与激光工程,2014,43:3597

[12]翟玉生,张志峰,苏玉玲,等.激光与光电子学进展,2014,51:106