熔融沉积式3D打印路径优化算法研究

韩兴国　宋小辉　殷　鸣　陈海军　殷国富

(1.四川大学制造科学与工程学院， 成都 610065； 2.桂林航天工业学院机械工程学院， 桂林 541004；3.南安普顿大学环境与工程学院， 南安普顿 SO17 1BJ)

0　引言

熔融沉积式3D打印凭借高温将材料融化成液态，通过打印头挤出后固化，其材料主要是ABS和聚碳酸酯PC等[1]。3D打印是一个由点到线、由线到面、由面到三维实体逐层累积的过程，需进行大量的路径扫描工作，打印路径关系到零件打印效率和表面质量[2]，因此，对3D打印路径进行规划有广泛的应用需求，具有重要的理论价值和工程应用背景。

3D打印路径规划包含轮廓路径规划和填充路径规划，目前对轮廓路径规划的研究较少，填充路径规划方法较多，主要有平行扫描[3-5]、星形发散扫描[6]、分形扫描[7-8]、螺旋线扫描[9]和基于voronoi图的扫描[10]等。平行扫描法又称为zigzag法，应用极其广泛，为了提高3D打印的生产效率，许多学者提出了一些与之相关的路径规划算法[11-18]。

文献[11-18]提出的路径规划算法在一定程度上提高了3D打印效率和成型质量，但都有一定的局限性，未对填充子区域的合并和打印次序进行阐述，打印效率仍有进一步提升的空间，且对轮廓路径规划的研究较少，当打印零件截面轮廓包含的封闭环多且复杂时，轮廓路径规划不合理会影响打印效率。针对以上问题，本文提出一种熔融沉积式3D打印路径优化算法，通过最优扫描线角度选取、填充子区域合并和合并区域打印序列优化等一系列算法对填充路径合理规划，此外，提出一种基于蚁群算法的轮廓路径规划方法，合理规划各轮廓的打印顺序。

1　方法概述

3D打印是对零件逐层打印，零件每层切片轮廓的形状可能各不相同[19]。某零件切片后的截面图如图1所示，该截面包含9个封闭环，对层面轮廓各封闭环的打印次序进行规划，即轮廓路径规划，各封闭环之间为零件实体，以直线方式对各封闭环之间的区域进行填充，并对填充路径进行规划，3D打印的路径规划主要包括轮廓路径规划和填充路径规划，为了防止零件发生变形和翘曲，先进行轮廓打印，后进行填充打印。对零件的轮廓路径和填充路径进行合理、有效的规划，对于提高打印效率和打印质量具有重要的意义。本文所述路径规划方法实施步骤如下：

(1)对打印零件进行切片，形成层面轮廓，基于蚁群算法对层面轮廓中的各封闭环的打印次序进行规划。

(2)综合考虑效率因素和打印质量，确定各切片层填充区域扫描线的最优角度。

(3)将填充区域进行子区域划分，采用四点法将能够连续打印的子区域进行合并。

(4)采用临近算法对合并后的各区域打印次序进行优化。

图1　某零件截面轮廓图Fig.1　Skeleton map of part cross-section

2　轮廓路径规划

对零件进行切片，得到各切片层的截面图，截面轮廓是由n条封闭曲线(封闭环)构成，轮廓路径规划就是对封闭环逐个打印。每个封闭环需确定一个打印起点，也是终点，整个截面中有n个起始点，不难看出，轮廓的路径规划问题可归结为经典的旅行商问题 (Traveling salesman problem, TSP), 即在n个起始点中寻找一条最优路径，使每个起始点只被穿越一次，这样可以减少零件的打印时间。

2.1　封闭环起始点确定

确定起始点的原则是每个封闭环仅有一个起始点且各封闭环的起始点之间的距离最小，本文采用一种改进的近邻法确定起始点。假设截面轮廓包含n个封闭环，Loop={Loop1，Loop2，…，Loopn}，轮廓中所有封闭环由m个顶点构成，顶点集为P={P1，P2，…，Pn}，任一封闭环的顶点集为Pi={Pi1,Pi2,…,Pikn}，其中m=k1+k2+…+kn，确定起始点的具体步骤如下：

(1)取顶点集P中第1个顶点P11作为封闭环P1的起始点，令S1=P11，并将P1从P中去除。

(2)依次求解顶点S1到P中各点的距离，将距离顶点S1最近的顶点Pij(1≤j≤ki)取出，令S2=Pij，并将Pi从P中去除。

(3)按照步骤(2)的思路，依次求解顶点Si到P中各点的距离，找到距离顶点Si最近的顶点作为Si+1，依次遍历所有的未访问封闭环顶点集，直到在P中的最后1个封闭环中找到Sn，依次求出S3,S4,…,Sn，可得起始点集C1={S1,S2,…，Sn}。

(4)依次求解C1中相邻两点间的距离，并求和d1=S1S2+S2S3+…+Sn-1Sn+SnS1。

(5)依次选取P中的顶点作为相对应封闭环的起始点，按照步骤(1)～步骤(4)的思路，可依次求解出m个起始点集Cr，并求出相对应的dr，其中，1≤r≤m。

(6)比较d1，d2，…，dm之间的大小，将最小的dr对应的Cr作为最优的起始点集。

其中，若封闭环由非直线的曲线构成，可取该封闭环的几何重心作为该封闭环的伪顶点，即该封闭环只有一个顶点，求过伪顶点和前一个封闭环的起始点的直线，该直线和封闭环的交点作为该封闭环的起始点。

2.2　基于蚁群算法的轮廓路径规划

蚁群算法是20世纪90年代初提出的一种模拟进化算法，主要用于解决组合序列优化问题，典型的应用案例就是旅行商问题[20]。

用改进的近邻法确定各封闭环的起始点后，将各环起始点作为待访城市，假设蚂蚁群体中蚂蚁的个数为u，封闭环的个数为v，封闭环i的起始点与封闭环j的起始点之间的距离为dij(i,j=1,2,…,v)，t时刻封闭环i起始点与封闭环j起始点连接路径上的信息素浓度为τij(t)，蚂蚁w(w=1,2,…,u)根据各封闭环起始点连接路径上的信息素浓度决定其下一个访问的城市，从封闭环i的起始点转移到封闭环j的起始点的概率公式为

(1)

其中

式中ηij(t)——启发函数

alloww——蚂蚁w待访封闭环起始点的集合

α——信息素重要程度因子

β——启发函数重要程度因子

当所有蚂蚁完成一次循环后，各封闭环起始点连接路径上的信息浓度需要重新更新，即

(2)

Δτij——所有蚂蚁在封闭环i的起始点与封闭环j的起始点之间的路径上释放的信息素浓度之和

ρ——信息素的挥发程度系数，0<ρ<1

(3)

式中Q——蚂蚁循环一次所释放的信息素总量，Q为常数

Lw——第w只蚂蚁经过路径的长度

综上所述，采用蚁群算法确定各封闭环打印次序的最优解，主要包括初始化参数、构建解空间、更新信息素和判断是否终止4个步骤，其具体步骤如图2所示。

图2　蚁群算法求解封闭环打印次序最优解的步骤Fig.2　Steps of solving optimal solution of closed loops printing order based on ant colony algorithm

2.3　轮廓路径规划实例

对图1中的零件进行轮廓路径规划，其截面包含9个封闭环，采用改进的近邻法确定各封闭环的打印起始点，采用蚁群算法寻找打印各封闭环的最优次序，设蚂蚁数量为50，迭代次数为200，可得最优的轮廓路径规划如图3所示。图4给出了用蚁群算法求解轮廓路径的平均轨迹长度和最短轨迹长度。

图3　基于蚁群算法的轮廓路径规划图 Fig.3　Contour path planning of part based on ant colony algorithm

图4　基于蚁群算法的轨迹长度比较Fig.4　Trajectory length comparison of ant colony algorithm

图5　基于zigzag法的轮廓路径规划Fig.5　Contour path planning of part based on zigzag

将图1所示零件按传统的平行扫描路径规划方法(zigzag法)进行轮廓路径规划，其轮廓路径规划如图5所示。将本文提出的方法与zigzag法进行比较，本文方法的每层轮廓路径长度为196.81 mm, zigzag法的轮廓路径长度为244.45 mm，轮廓路径长度缩短了19.5%。

3　填充路径规划

填充路径规划是在零件的某切片截面层上封闭轮廓间区域的填充次序进行合理规划，本文采用平行扫描填充内部轮廓，在边界线内往复扫描，平行扫描示意图如图6所示。影响平行扫描法打印质量和效率的主要因素有扫描线角度选取、填充子区域合并和合并区域打印序列优化，这3个影响因素决定了3D打印的效率和精度。

图6　平行扫描路径生成示意图Fig.6　Scheme of path generation based on direction-parallel scanning method

3.1　选取最优的扫描线角度

平行扫描的路径主要由直线构成，各直线相互平行，每条直线路径结束后，打印喷头停止运动，直线运行至下一条扫描线的起点，继续直线扫描打印，循环往复，如图7所示。打印过程中，打印喷头必然反复启停，不能无间断运动，在拐角处只能低速运行并且存在启停和加减速问题，影响打印效率且这些区域易引起零件变形、翘曲等问题[11]。为减少这些问题，须减少平行扫描中拐角的存在，而拐点的数量和扫描线的角度存在必然的联系。

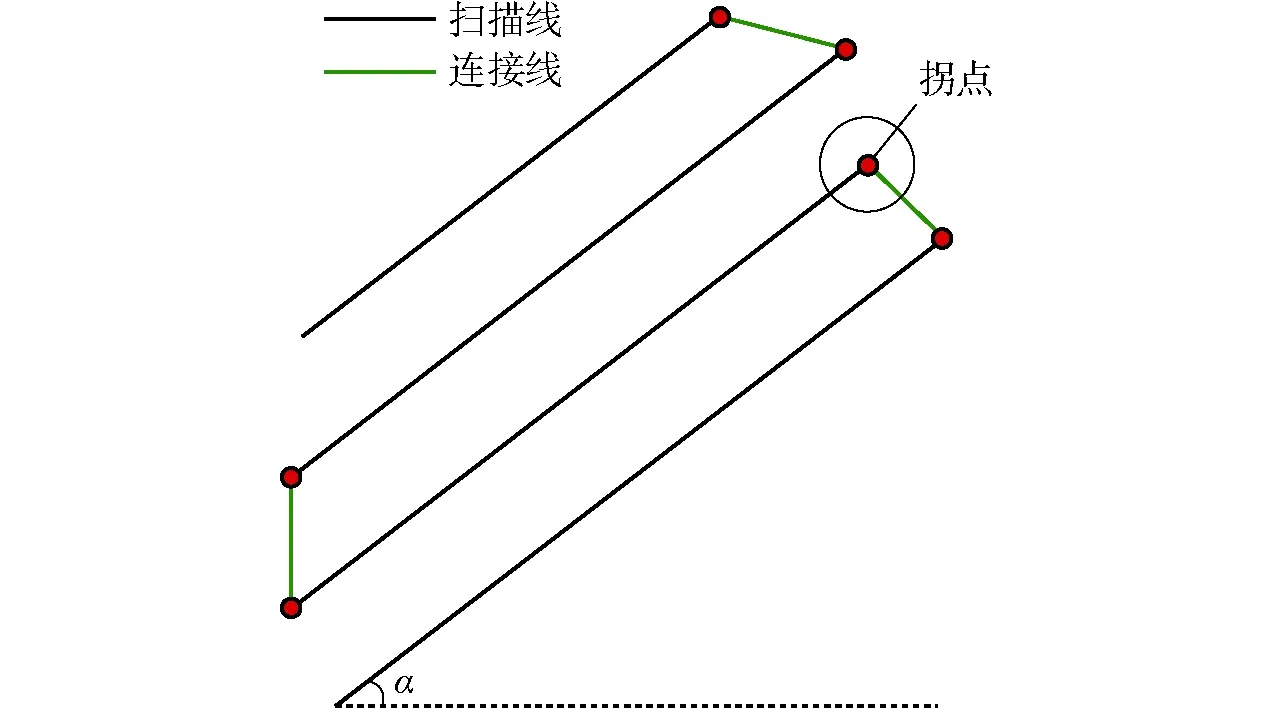
图7　直线扫描路径Fig.7　Direction-parallel scanning method

假设零件的某一切片轮廓由封闭曲线f1(x)、f2(x)、…、fn(x)构成，假设扫描线角度为α(0≤α≤π)，则第1条扫描线的直线方程为

g1(x)=kx+b1

(4)

其中

k=tanα

式中b1——第1条扫描线截距

k——扫描线斜率

第m条扫描线的方程为

gm(x)=kx+b1+(m-1)b

(5)

式中b——两相邻扫描线之间的距离，即打印头喷嘴直径

直线g1(x)分别与f1(x)、f2(x)、…、fn(x)的交点数构成集合U1={u11，u12，…，u1u}，同理，gm(x)分别与f1(x)、f2(x)、…、fn(x)的交点个数构成集合U1={um1，um2，…，umn}，可得第1条扫描线和第m条扫描线于各封闭曲线交点数之和为

Usum1=u11+u12+…+u1n

(6)

Usumm=um1+um2+…+umn

(7)

扫描线所构成的直线方程和封闭曲线f1(x)、f2(x)、…、fn(x)的交点即为平行扫描的拐点位置，假设在打印零件的一个切片层面所构成的封闭空间中有m条扫描线，则该层面拐点数总共为Usum，即

Usum=Usum1+Usum2+…+Usumm

(8)

当扫描线的角度α取不同值时，拐点数也不同，若打印效率最高，需拐点数为最小，即

Usummin=min(Usum(α))(0≤α≤π)

(9)

拐点数量不仅影响打印效率，对打印质量也有影响。由于扫描线在拐角处频繁的起停、加速和减速，容易在打印零件的边缘处造成打印材料熔融沉积时分布不均，表面光滑度较差，在边缘处，有的位置材料熔融沉积2次，有的位置无材料沉积，如图8所示。重复沉积区域和无沉积区域面积相等，与拐角的角度有关，如图9所示，具体推导如下

S=S△OCA+S△OCB-SOAB

(10)

式中S——重复沉积或无沉积区域面积

S△OCA——三角形OCA的面积

S△OCB——三角形OCB的面积

SOAB——扇形OAB的面积

根据平面几何知识，可得

(11)

式中r——打印喷头半径

θ——扫描线拐角的角度

图8　拐角处材料沉积示意图Fig.8　Deposition scheme at corners

图9　拐角处的材料沉积情况分析Fig.9　Deposition analysis scheme at a corner

图10　不同角度下的零件(图6)扫描图Fig.10　Tool-path of part (as shown in Fig.6) with different inclinations

根据以上分析可知，拐角的数量越多，拐角处重复扫描区域和未扫描区域越多，表面质量越粗糙，并且在拐角处由于电机反复起停和加减速，导致零件打印时间变长，因此控制拐角数量，对打印质量和效率具有重要的影响。扫描线与截面交点数和拐点数量相等，扫描线角度不同，拐点数量不同。图6零件在不同角度下的截面扫描图如图10所示。

假设扫描线宽度(喷头直径)为0.4 mm，对图1和图6中的切片截面轮廓进行扫描线角度优选，拐点个数与扫描线角度关系如图11所示，不难看出，图1所示零件在扫描线角度为0°(或180°)时，拐点个数最少；图6零件在扫描线角度为90°时，拐点个数最少。

为实现应力分散，选取相邻两层之间的扫描线相互垂直，因此，本文提出的扫描线角度为每两层选取一次。此外，本文算法采用完整的区域填充扫描方式，实际应用中也可采用镂空内部加支撑的扫描方式。

3.2　扫描区域的合并

扫描线角度确定后，扫描线与切片轮廓之间形成一些封闭的区域，每个区域由一系列的扫描线往复扫描构成，每个区域包含4个关键点，即该区域第一条扫描线的起点和终点、最后一条扫描线的起点和终点。3D打印过程中， 需对每个区域逐一扫描，扫描策略是先扫描临近区域，后扫描非临近区域，非临近区域的扫描，需要打印喷头进行一段空行程运动，降低了效率，所以在打印时可对连续打印的临近区域进行合并，合并后的区域可以一次扫描完毕，连续打印且无空行程运动。本文采用四点法对一些相邻子区域进行合并。

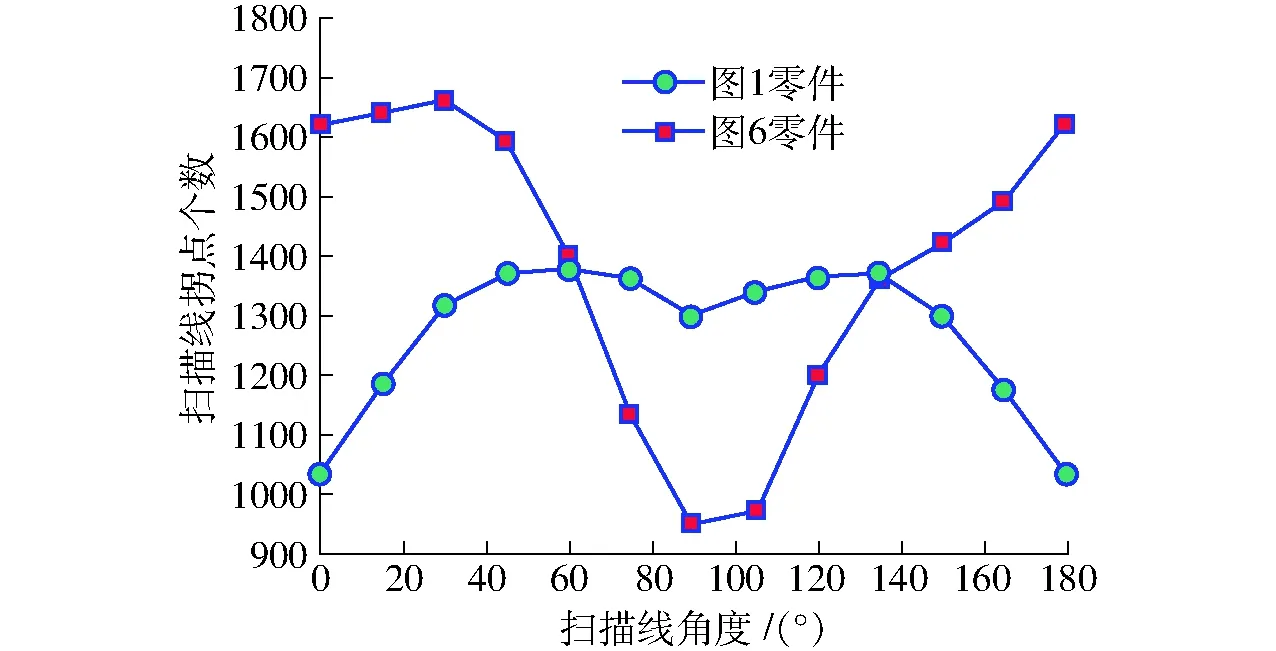
图11　拐点个数和扫描线角度关系Fig.11　Relationship between corner quantity and scanning line angle

四点法：若某子区域的最后一条扫描线的终点是另一子区域第一条扫描线的两个端点之一，可将该端点作为另一子区域的起点，将这两个子区域合并。基于四点法的扫描区域的合并算法如下：

(1)扫描线角度确定后，假设打印零件切片截面图被划分为n个子区域。

(2)每个子区域包含4个关键点，即该区域第一条扫描线的起点和终点、最后一条扫描线的起点和终点，建立n×4维矩阵数组A，对子区域关键点信息按从左到右、从上到下次序进行存储，则A为

(9)

式中mik——第i个子区域的第k个点，1≤i≤n;1≤k≤4

mi1、mi2——第i个子区域起始扫描线的端点

mi3、mi4——第i个子区域最后一条扫描线的端点

(3)令子区域编号i=1，假设合并后的区域数为u，令合并后子区域编号j=1，确定第i个子区域的起点mistart=mi1，假如该子区域扫描线的数量为奇数，则该区域的终点miend=mi4，假如该子区域扫描线的数量为偶数，则该区域的终点miend=mi3，令合并后的第j个子区域起点sjstart=mi1。

(4)查阅编号为i+1至n的子区域中所有点，判断是否存在某点坐标值等于miend，若存在该点，则执行第5步，若不存在该点，则执行第6步。

(5)若第t(i+1≤t≤n)区域存在和miend相同的点，将矩阵第t行移至第i+1行，第i+1行至第t-1行下移一行，令i=i+1，mistart=m(i-1)end，根据第i区域中扫描线的奇偶性，按步骤(3)所示方法确定miend，执行第7步。

(6)若剩余区域内不存在和miend相同的点，则令sjend=miend，然后令j=j+1，i=i+1，mjstart=mi1，根据第i区域中扫描线的奇偶性，按步骤(3)所示方法确定miend，执行第7步。

(7)判断i是否等于n+1，若不相等，执行第4步，若相等，则程序结束，合并后区域构建起始点矩阵为s，s为

(10)

式中u——合并区域数量

sjstart——第j合并区域的起点，1≤j≤u

sjend——第j合并区域的终点，1≤j≤u

某零件的截面划分子区域如图12所示，共包含12个子区域，根据该算法，合并后区域如图13所示，共包含4个区域。

图12　零件截面区域划分Fig.12　Area partition of part cross-section

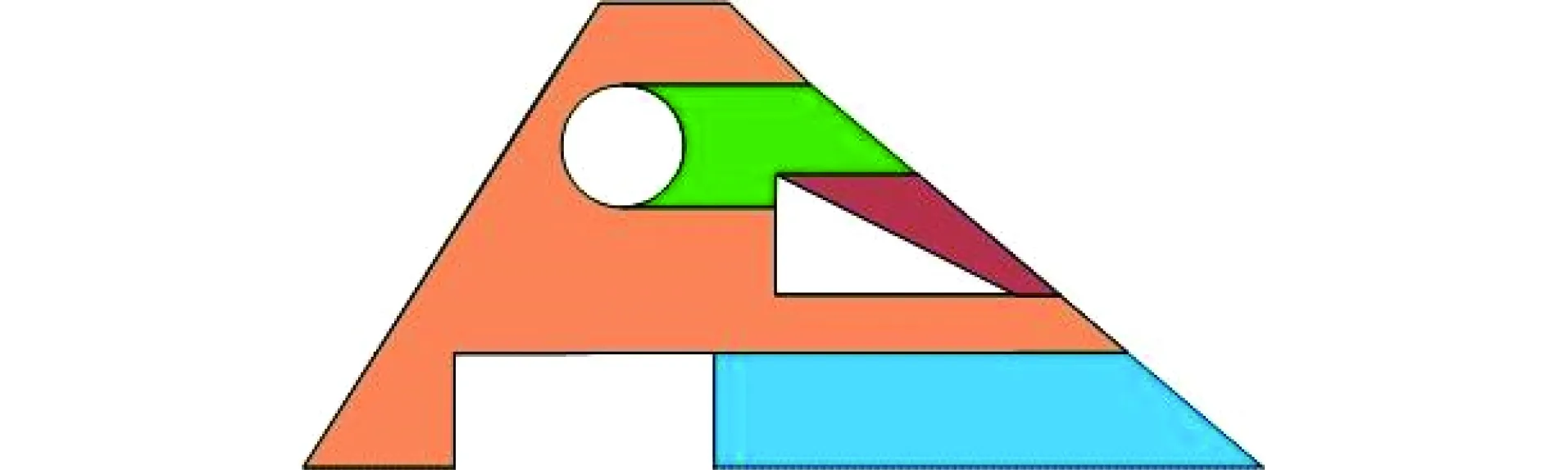
图13　零件截面区域划分合并Fig.13　Area merging of part cross-section

3.3　合并区域的打印次序优化

扫描区域合并后，需对合并后的区域逐一打印，考虑效率因素，打印次序需满足各合并区域间的空行程路径之和最短，这里采用一种临近算法，具体步骤如下：

(1)构建合并区域的起始点矩阵s，如式(10)所示，令j=1，则sjstart=s1start，sjend=s1end。

(2)从矩阵s的第j+1行起，寻找距离sjend最小的点，若该点在第t(j+1≤t≤u)行，则将矩阵s第j+1行和t行互换位置。

(3)若s(j+1)end与sjend距离最短，将s(j+1)end和s(j+1)start的值互换，若s(j+1)start与sjend距离最短，则保持不变。

(4)令j=j+1，判断j是否等于u，若不相等，则执行步骤(2)，否则，程序结束，矩阵s中各区域的起始点次序即为最终的合并区域进行打印次序。

对图13中的合并区域按上述方法进行打印次序优化，打印次序按(A1-A2)-(B1-B2)-(C1-C2)-(D1-D2)进行，如图14所示。

图14　合并区域打印次序Fig.14　Printing order of merging areas

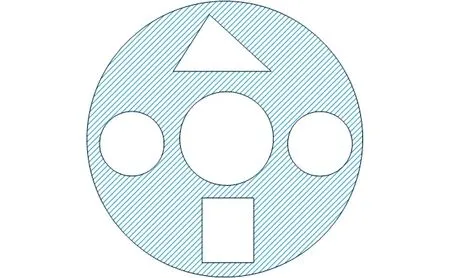
图15　某零件截面轮廓图Fig.15　Skeleton map of part cross-section

4　实验

为证明上述路径规划方法的可行性，对图15所示零件进行路径规划，该零件截面包含6个封闭轮廓，采用改进的近邻法确定各封闭环的打印起始点，采用蚁群算法寻找打印各封闭环的最优次序，设蚂蚁数量为50，迭代次数为200，可得最优的轮廓规划路径如图16所示。

对图15所示零件进行切面轮廓填充，不同角度下扫描线的拐点情况如图17所示，不难看出，当扫描线角度为或时，扫描线的拐点个数最小，考虑效率和精度的因素，选择扫描线角度为0°。

图16　轮廓路径规划图Fig.16　Contour path planning-graph

图17　拐点个数与扫描线角度关系曲线Fig.17　Relationship curve between corner quantity and scanning line angle

图18　截面子区域划分图Fig.18　Sub-region division of part cross-section

图19　截面子区域合并图Fig.19　Sub-region merging of part cross-section

对图15所示切片截面进行区域划分，划分后的区域如图18所示，共包含16个子区域。按照四点法对划分后的子区域进行区域合并，合并后的区域如图19所示，共包含6个区域。按本文所示方法对合并区域的打印次序进行优化，如图20所示，打印次序按(A1-A2)-(B1-B2)-(C1-C2)-(D1-D2)-(E1-E2)-(F1-F2)进行。

图20　合并区域打印次序图Fig.20　Printing order of merging regions

图21　悬臂式3D打印实验平台Fig.21　Cantilever 3D printing robot experiment platform1.人机交互界面　2.控制系统　3.垂直导轨　4.水平导轨　5.挤出机　6.工作台　7.底座

在图21所示的悬臂式3D打印实验平台上进行实验，该打印装置控制系统选用倍福控制器C6920，该控制器采用面向工业4.0的EtherCAT总线，具有较强的实时性能和灵活性，采用Win7操作系统，基于Twincat 2软件采用NCI控制指令调用控制程序控制各轴联动实现3D打印功能，按本文提出的路径优化方法对路径进行规划。

对图1、图12和图15所示零件进行打印，打印材料为ABS，喷嘴直径0.4 mm，零件分层厚度0.2 mm，喷头打印移动速度是120 mm/s，空程速度是160 mm/s，打印零件如图22～24所示。

图22　图1所示零件打印图Fig.22　Printing part (as shown in Fig.1)

图23　图12所示零件打印图Fig.23　Printing part (as shown in Fig.12)

图24　图15所示零件打印图Fig.24　Printing part (as shown in Fig.15)

将本文提出的路径规划算法与传统的zigzag法进行比较，打印时间和轮廓长度情况如表1所示。由表1可以看出，本文提出的路径规划算法在打印时间和单层轮廓路径长度方面比传统的zigzag法都有所降低，图1零件打印时间比zigzag法缩短了12.6%，轮廓路径长度缩短了19.5%，图12零件打印时间比zigzag法缩短了11.6%，轮廓路径长度缩短了12.5%，图15零件打印时间比zigzag法缩短了8.9%，轮廓路径长度缩短了10.7%，由此可见，打印效率明显提高。

表1　打印时间和轮廓长度比较Tab.1　Comparison between two methods about printing time and contour length

针对3D打印的尺寸精度情况，将本文提出的路径规划算法与传统的zigzag法进行比较，对2种方法打印图1所示零件的尺寸进行测量，如表2所示。

表2　尺寸精度比较Tab.2　Dimension accuracy comparison　mm

针对3D打印的表面质量情况，将本文提出的路径规划算法与传统的zigzag法进行比较，对2种方法打印零件(图1、图12、图15)上表面和侧面的表面粗糙度进行测量，测量结果如表3所示。

由表2可以看出，按本文方法打印的图1零件长、宽、高尺寸偏差分别为0.248、0.144、0.141 mm，按传统的zigzag法打印图1零件长、宽、高的尺寸偏差分别为0.386、0.275、0.221 mm，可见按本文方法打印的零件尺寸精度有所提升。

由表3可以看出，按传统的zigzag法打印的零件的上表面粗糙度Ra在18～20 μm之间，轮廓最大高度Rz为235～250 μm；侧面粗糙度Ra为10～12 μm，轮廓最大高度Rz在110～130 μm之间。按本文方法打印的零件的上表面粗糙度Ra在13～15 μm之间，轮廓最大高度Rz为200～211 μm；侧面粗糙度Ra在6.5～7.0 μm之间，轮廓最大高度Rz在90～100 μm之间。由此可见，采用本文提出的路径规划算法和传统算法相比，打印零件的表面质量有所改善。

表3　表面粗糙度比较Tab.3　Surface roughness comparison　μm

需要注意的是，不同的打印条件和环境、不同的打印设备，所测量的尺寸精度和表面粗糙度是不同的，因此，本文所测量的尺寸精度和表面粗糙度是在特定的打印条件下和打印设备上测量的，不具有广泛的普适性，但是，采用本文提出的路径规划算法和传统算法相比，本文算法在尺寸精度和打印质量的提升是显而易见的。

5　结论

(1)采用蚁群算法对熔融沉积式3D打印轮廓路径的打印序列进行优化，寻求最短的轮廓打印路径，以提高打印效率。

(2)综合打印效率和加工表面质量等因素，选择最优的扫描线角度，提出了一种基于四点法的打印区域合并算法，采用临近法对合并区域的打印次序进行优化，从而改善熔融沉积式3D打印填充效率和质量。

(3)实验结果表明：本文算法与传统的zigzag法相比较，3组零件单层的轮廓路径长度分别缩短了19.5%、12.5%、10.7%，打印时间缩短了12.6%、11.6%、8.9%，提高了打印效率，能够快速、有效地进行3D打印，无翘曲和变形产生。此外，本文算法与传统的zigzag法相比较，打印零件的尺寸精度和表面质量都有一定提高。实验结果验证了该路径规划算法的可行性和有效性。

1杨建军，张志远，兰洪波，等. 基于EHD微尺度3D打印喷射机理与规律研究[J/OL]. 农业机械学报, 2016, 47(6): 401-407.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20160653&flag=1.DOI:10.6041/j.issn.1000-1298.2016.06.053.

YANG Jianjun, ZHANG Zhiyuan, LAN Hongbo, et al. Jetting mechanism and rules of micro scale 3D printing based on EHD[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(6):401-407. (in Chinese)

2刘利刚, 徐文鹏, 王伟明, 等. 3D打印中的几何计算研究进展[J]. 计算机学报, 2015, 38(6): 1243-1267.

LIU Ligang, XU Wenpeng, WANG Weiming, et al. Survey on geometric computing in 3D printing[J]. Chinese Journal of Computers, 2015, 38(6): 1243-1267. (in Chinese)

3ASIABANPOUR B, KHOSHNVIS B. Machine path generation for the SIS process[J]. Robotics and Computer-Integrated Manufacturing, 2004, 20(3): 167-175.

4TARABANIS K A. Path planning in the proteus rapid prototyping system[J]. Rapid Prototyping Journal, 2001, 7(5):241-252.

5YANG Y, LOH H T, FUH J Y H, et al. Equidistant path generation for improving scanning efficiency in layered manufacturing[J]. Rapid Prototyping Journal, 2002, 8(1): 30-37.

6ONUH S O, HON K K B. Application of the Taguchi method and new hatch styles for quality improvement in stereolithography[J]. Journal of Engineering Manufacture, 1998, 212(6):461-472.

7YANG J, BIN H, ZHANG X, et al. Fractal scanning path generation and control system for selective laser sintering(SLS) [J]. International Journal of Machine Tools and Manufacture, 2003, 43(3):293-300.

8CHIU W K, YEUNG Y C, YU K M. Toolpath generation for layer manufacturing of fractal objects[J]. Rapid Prototyping Journal, 2006, 12(4): 214-221.

9ZHAO Haisen, GU Fanglin, JORGE G, et al. Connected fermat spirals for layered fabrication[J]. ACM Transactions on Graphics, 2016, 35(4):100.

10KIM D S. Polygon offsetting using a Voronoi diagram and two stacks[J]. Computer-Aided Design, 1998, 30(14):1069-1076.

11BRANDLEY T, HWAN-SIK Y. Efficient path planning algorithm for additive manufacturing systems[J]. IEEE Transactions on Components, Packaging and Manufacturing Technology,2014, 4(9):1555-1563.

12RAJAN V T, SRINIVASON V, KONSTANTIONS A T. The optimal zigzag direction for filling a two-dimensional region[J]. Rapid Prototyping Journal, 2001, 7(5):231-240.

13卞宏友，杨光，李英，等. 金属激光沉积成形分组平行扫描路径生成方法[J].机械工程学报，2013,49(11): 171-176.

BIAN Hongyou, YANG Guang, LI Ying, et al. Grouping parallel scan path generating method of metal laser deposition shaping[J].Journal of Mechanical Engineering, 2013,49(11):171-176.(in Chinese)

14卞宏友，刘伟军，王天然，等. 激光金属沉积成形的扫描方式[J].机械工程学报,2006,42(10):171-175.

BIAN Hongyou, LIU Weijun, WANG Tianran, et al. Scanning mode for laser metal deposition shaping[J]. Chinese Journal of Mechanical Engineering, 2006, 42(10): 171-175.(in Chinese)

15HAN Wenbiao, MOHSEN A J, STEPHEN C D, et al. Tool path-based deposition planning in fused deposition processes[J].ASME Journal of Manufacturing Science & Engineering,2002, 124(5):462-272.

16JIN Yuan, HE Yong, FU Jianzhong, et al. Optimization of tool-path generation for material extrusion-based additive manufacturing technology[J].Additive Manufacturing, 2014(4): 32-47.

17史玉升, 钟庆, 陈学彬, 等. 选择性激光烧结新型扫描方式的研究及实现[J]. 机械工程学报, 2002, 38(2): 35-39.

SHI Yusheng, ZHONG Qing, CHEN Xuebin, et al. Research and implement of a new kind of scanning mode for selective laser sintering[J].Chinese Journal of Mechanical Engineering, 2002, 38(2):35-39. (in Chinese)

18黄雪梅, 牛宗伟, 董小娟. 快速成型技术中的分区扫描路径产生算法[J]. 机械设计与研究,2007, 23(1): 80-82.

HUANG Xuemei, NIU Zongwei, DONG Xiaojuan. An algorithm of sub-regional scanning path generation for rapid prototyping manufacturing[J]. Machine Design and Research, 2007, 23(1):80-82. (in Chinese)

19李大伟，戴宁，姜晓通，等. 密度感知的3D打印内部支撑结构轻量化建模[J].计算机辅助设计与图形学学报, 2016,28(5): 841-848.

LI Dawei, DAI Ning, JIANG Xiaotong, et al. Density aware internal supporting structure light-weighting modeling of 3D printed objects[J]. Journal of Computer-Aided Design & Computer Graphics,2016, 28(5): 841-848.(in Chinese)

20刘建华，杨建国，刘华平，等. 基于势场蚁群算法的移动机器人全局路径规划方法[J/OL]. 农业机械学报，2015, 46(9):18-27.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20150903&flag=1.DOI: 10.6041/j.issn.1000-1298.2015.09.003.

LIU Jianhua, YANG Jian’guo, LIU Huaping, et al. Robot global path planning based on ant colony optimization with artificial potential field[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(9):18-27. (in Chinese)