极限安全地震动下核电站安全壳楼层反应谱*

兀琼，刘玉岚，王彪

(1.中山大学工学院, 广东 广州 510275；2. 中山大学中法核工程与技术学院, 广东 广州 510275)

发展核电是解决能源问题一个有效的途径，而核电站的安全一直备受人们的关注。核电站安全壳作为抗震Ⅰ类结构，在地震载荷下不仅需要保证正常运行的安全性，而且需要确保结构的完整性。因此，分析安全壳在地震作用下的响应对核电站结构设计和安全性评估有很重要的意义。

核电站安全壳结构[1]按照材料类型可分为钢结构、钢筋混凝土结构和预应力混凝土结构。核电站CPR1 000安全壳结构属于预应力混凝土结构。现阶段核电站安全壳楼层反应谱分析主要采用集中质量模型或者简化的三维模型。集中质量模型是基于与原实体模型质量、刚度等效的原则而建立的多质点集中质量-梁单元模型。Varpasuo[2-3]最早提出了用简化的杆系模型模拟核电站厂房。为了考虑结构的弹塑性行为，Takeda等[4]建立的核电厂安全壳模型以三线性滞回模型模拟钢筋混凝土剪力墙，随后又通过试验建立了钢筋混凝土构件的恢复力模型，奠定了模拟钢筋混凝土弹塑性行为的基础。2002年Kobayashi等[5]提出了多质点集中质量-剪力弯曲模型，对台湾莲花核电厂1/4比例尺实验模型进行了时程分析。国内研究者李忠献等[6-7]采用集中质量模型分析了土-结构的相互作用对核电站CPR1 000安全壳的影响。集中质量模型大大减少了计算的自由度数，在楼层谱分析中应用较方便，但其无法观测结构内部的应力响应。Rotaru等[8]对CANDU700建立了粗略的三维模型，并比较了时域和频域分析的区别。Nakamura等[9]建立了某PWR核电站的简化模型以进行抗震风险评估。随着计算机技术的发展，详细的三维有限元模型不仅能够进行楼层反应谱分析，而且能真实地模拟核电站厂房的地震响应。

楼层反应谱反映了单自由度体系在主次连接点振动下的最大响应与自身振动频率之间的关系，其分析方法主要有直接法和时程分析法[10]。直接法是利用随机振动的方法用地震动反应谱直接建立楼层反应谱，虽计算较快但因无法与时程分析结合而较少使用。时程分析方法是对结构进行时程分析后将其转化为楼层反应谱的方法。本文针对核电站CPR1 000安全壳结构建立了精细的三维有限元模型，考虑结构非线性分析了结构在极限安全地震动作用下的响应，评估了核电站安全壳结构的安全性，并选取关键楼层位置的代表点进行了楼层反应谱分析。

1　安全壳模型

1.1　物理模型

核电站CPR1 000安全壳结构属于预应力钢筋混凝土结构，主要由筒体、扁球壳形的穹顶和筏板基础三部分组成，内置0.006 m的钢衬里来防止放射物泄露。安全壳的总高度为66.68 m，其中筒体壁厚0.9 m，内径为37 m，筒体上部与壁厚为0.8 m的穹顶相连接，穹顶的半径为24 m。安全壳筒体还设有一个直径为7.4 m的设备闸门孔和两个直径为2.94 m的人员闸门孔。安全壳的几何剖面图如图1所示。

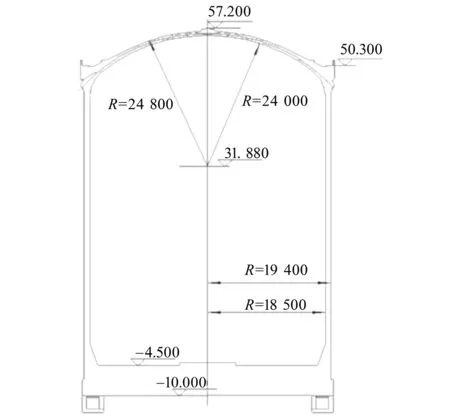
图1　安全壳结构的几何剖面图Fig.1　Geometric profile of containment

安全壳结构中的预应力钢束分布在安全壳筒体和穹顶上，包括分布在筒体内侧的竖向钢束(半径为18.85 m)、筒体外侧的两层环向钢束(半径为19.03和19.23 m)以及分布在扁球壳形穹顶处的预应力钢束。预应力钢束的方位信息和预应力值的确定参考文献[11]。

1.2　三维有限元模型

核电站安全壳三维有限元模型使用ABAQUS有限元分析软件建立。筒体、穹顶、基础部分的混凝土结构，采用C3D8R六面体有限单元模拟，内置的钢内衬选用S4壳单元类型，并且不考虑与混凝土结构间的相对位移。由于预应力钢束和普通钢筋数量较大、形式复杂，为了简化计算、方便模型的建立，忽略钢筋与混凝土之间的滑移，将其直接嵌入到混凝土结构中实现两者的相互耦合。基于Yonezawa等[12]的预应力筋模拟方式，采用T3D2杆单元模拟预应力钢束、用rebar surface层模拟普通钢筋。预应力的施加采用降温法实现，在ABAQUS中针对预应力钢束设置线膨胀系数和降温选项，通过温度降低和钢束收缩来实现混凝土预应力的施加[13]。基础变形对安全壳地震响应影响不大，计算中可不考虑基础的变形将其设置为刚性基础。图2-3分别是预应力钢束和普通钢筋的有限元模型，图4是安全壳的精细三维有限元模型。

安全壳结构选取强度等级为C50的混凝土材料，密度为2 500 kg/m3，弹性模量为33.6 GPa，泊松比为0.2，混凝土单轴抗拉强度标准值为2.65 MPa，单轴抗拉强度标准值为32.5 MPa。各部件的其他材料特性、屈服强度如表1所示。混凝土材料的非线性本构关系选用ABAQUS中的塑性损伤模型[14]，预应力钢束、普通钢筋以及钢内衬钢材则采取弹塑性模型模拟非线性。

表1　安全壳结构各部件的材料特性Table 1　Properties of each component of the containment

2　安全壳结构振动特性

确定结构的振动特性是动力分析的第一步，对结构进行模态分析就可以得到结构的自振频率和振型等动力特性。分析安全壳结构的动力特性时，将结构底部设置为固定端。安全壳结构前16阶模态频率信息和前四阶振型图如表2和图5所示。

由图5和相应的振型参与系数可知，第一阶和第二阶振型分别以水平x和y方向为主，对应频率分别为4.245和 4.262 Hz；两个方向的频率近似相同，可见结构在x和y方向的动力响应接近。以z向为主的振型出现在第十二阶模态，因而x和y方向是结构的主要运动方向。安全壳结构的固有周期是0.235 s，固有周期较小，说明安全壳结构具有很大的刚度。

图3　普通钢筋的有限元模型Fig.3　Model of ordinary steels

图4　安全壳的精细三维有限元模型Fig.4　Detailed 3D finite element model of containment

模态12345678周期/s0.2350.2350.1540.1540.1340.1330.1180.115频率/Hz4.2544.2626.4826.5157.4487.5128.4968.730模态910111213141516周期/s0.1130.0800.0790.0790.0770.0770.0770.076频率/Hz8.85612.53812.59312.63912.97313.01013.05513.203

图5　安全壳的前四阶振型Fig.5　The first four order mode of containment

3　结构在极限安全地震动下的响应分析

3.1　边界条件和载荷输入

抗震分析过程中，将结构底部设置为固定端。本文计算安全壳在极限安全地震动下的响应，选取人工合成的LBNS基准地震动加速度时程作为地震载荷输入，其水平x方向加速度峰值为0.2g，竖直z向加速度峰值为0.133g，g为重力加速度，地震记录总持时为30 s，时间步长为0.01 s。在采用直接积分法求解结构时程响应时，选取瑞利阻尼确定结构的阻尼矩阵。图6为水平x和竖直z向的LBNS地震动加速度时程曲线。参考文献[15]可知，钢筋混凝土结构临界阻尼比一般是在3% ～ 8%之间，本文取临界阻尼比为3%。为了分析地震动的哪些频率分量对结构的影响较大，采用傅氏变换将地震动加速度时程的时域数据转化为频域数据。图7是将x和z向地震动经傅式变换后得到的傅式频谱图。从图7可以看出，地震波频谱的幅值集中在0 ～ 10 Hz频率段内，这部分频率或者周期对应着地震动的卓越频率特性；在结构固有频率接近该频率段时，结构的响应达到最大。

图6　地震动加速度时程曲线Fig.6　Acceleration time history of ground motion

3.2　应力云图

采用降温法对预应力钢束施加预应力，图8是预应力钢束的最大主应力云图。图8中，预应力钢束沿着钢束轴线方向的应力值比较接近；在闸门口和两个设备孔附近的应力值稍有变化，这是因为预应力钢束在孔口附近发生弯曲引起的。安全壳结构主要沿着水平方向运动，水平x向地震动加速度峰值是0.2g。安全壳混凝土结构在地震动峰值所对应的时刻为3.1 s，图9是地震动加速度峰值对应时刻的最大主应力云图。

从图9中可以看出，在地震载荷下混凝土结构大部分处于压应力状态，而结构的设备孔附近、环梁、扶壁柱周围以及与基础相连的底部都出现了拉应力，这些位置将是最先也最容易受到影响的区域。根据文献[14]中的混凝土材料的拉伸应力应变关系，混凝土受拉破坏时应力应为混凝土抗拉强度标准值。3.1 s时混凝土的最大拉应力为2.08 MPa，小于混凝土的抗拉强度标准值2.65 MPa，因此在该极限安全地震动作用下，安全壳的混凝土结构不会产生损伤，结构依然处于弹性阶段且保持良好的完整性。

图7　地震动傅式频谱图Fig.7　Fourier spectrum of ground motion

图8　预应力钢束的最大主应力云图Fig.8　Maximum principal stress contours of prestressed tendons

图9　混凝土结构在3.1 s时的最大主应力云图Fig.9　Maximum principal stress contours of the concrete structure at 3.1 s

3.3　楼层反应谱分析

楼层反应谱反映了单自由度体系在主次连接点振动下的最大响应与自身振动频率之间的关系。在不考虑主次结构耦合的情况下，对核电站的子结构进行抗震分析，只需要根据子结构的振动特性和生成的楼层反应谱就可直接得到子结构的响应。本文采用时程分析方法对核电站安全壳结构进行楼层反应谱分析。

(1)

式中，λ和ω分别是单自由度体系的阻尼比和自振频率。反应谱体现的是在一定阻尼比下结构的最大响应与结构自振特性之间的关系，其加速度响应的最大值为：

(2)

楼层加速度反应谱即S(ω,λ)值与自振频率ω的关系曲线。本文选取安全壳结构的五个关键楼层作为观察点，计算相应的楼层反应谱。目标阻尼比为5%时，两个楼层位置即穹顶顶点(标高为+56.68 m)和标高为+39.14 m的楼层加速度反应谱如图10-11所示。分析楼层反应谱曲线的三个主要参数分别是楼层加速度反应谱的加速度峰值、峰值对应的频率和零周期对应的加速度值[17]。表3是观察点的楼层反应谱的特征值。

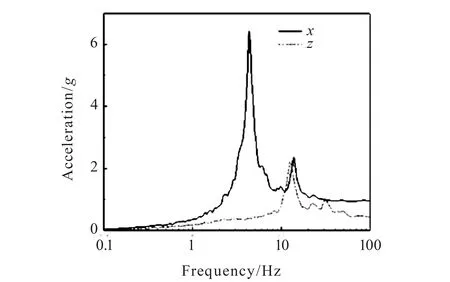
图10　穹顶顶点的楼层反应谱Fig.10　Floor response spectrum of dome

从图10-11可以看出，结构的x向楼层反应谱峰值所对应的频率是4.34 Hz，与结构自由振动的固有频率4.245 Hz很接近，在误差允许的范围内。结合表3的数据，可以发现结构的水平楼层反应谱幅值在结构固有频率附近时最大，z向楼层反应谱峰值对应的频率接近于以z向为主的模态频率，所以结构楼层反应谱主要受结构自振特性的影响。另外，当安全壳楼层上子结构的固有频率处在安全壳结构的固有频率附近时，会出现因共振而产生的响应放大现象。

图12是目标阻尼比2%、5%、7%和10%时，穹顶顶点的楼层反应谱。经比较发现，其x向楼层反应谱峰值随着目标阻尼比的增加而逐渐减小，而峰值对应的频率和零周期加速度值却没有变化，所以结构的目标阻尼比主要是对楼层反应谱的峰值产生影响。

图11　标高为39.14 m的楼层的楼层反应谱Fig.11　Floor response spectrum of floor at 39.14 m

图12　穹顶顶点不同阻尼比下的x向楼层反应谱Fig.12　Floor response spectra of dome with different damping ratios

观察点加速度峰值/g(x向/z向)峰值对应的频率/Hz(x向/z向)零周期对应的加速度/g(x向/z向)穹顶顶点6.432/2.1924.34/12.500.927/0.402标高+50.30m的楼层5.733/1.8074.34/12.500.894/0.391标高+45.80m的楼层5.304/1.3594.34/12.500.737/0.376标高+39.14m的楼层4.456/1.2194.34/12.500.626/0.259标高+29.90m的楼层3.290/1.0554.34/12.500.567/0.249

4　结　论

建立了核电站CPR1 000安全壳结构的精细三维有限元模型。考虑材料非线性特性，在极限安全地震载荷作用下，进行结构的抗震分析。主要结论如下：

1)运用CPR1 000安全壳结构的精细三维有限元模型，分析与主结构相连的子结构的地震响应时，不需要重新对主结构进行抗震分析，可直接将结构的楼层反应谱作为子结构地震分析的输入。

2)在容易发生应力集中的设备孔附近、环梁和扶壁柱周围以及与基础相连的底部位置处的最大拉应力小于混凝土的抗拉强度。所以，在极限安全地震动作用下混凝土结构依然处于弹性阶段，保持着良好的完整性和安全性。

3)从楼层反应谱分析可以看出，结构的楼层反应谱特性主要受到结构自振特性的影响。结构的目标阻尼比只影响峰值的大小而不改变峰值对应的频率和零周期加速度。在安全壳楼层上安置子结构时，应该避免设置与安全壳结构自振特性接近的子结构。

参考文献：

[1]余爱萍, 王远功. 核反应堆安全壳结构形式的选择 [J]. 核动力工程, 1989(4): 14-17.

YU A P, WANG Y G. The selection of structural form of nuclear reactor containment [J]. Nuclear Power Engineering, 1989(4): 14-17.

[2]VARPASUO P. The seismic reliability of VVER-1 000 NPP prestressed containment building [J]. Nuclear Engineering and Design, 1996, 160(3): 387-398.

[3]VARPASUO P. The development of the floor response spectra using large 3D model [J]. Nuclear Engineering and Design, 1999, 192(2/3): 229-241.

[4]TAKEDA M, OHKAWA Y, AKUTSU Y. An evaluation method for seismic isolation effect in siting of a nuclear facility [J]. Reliability Engineering and System Safety, 1998, 62(3): 241-249.

[5]KOBAYASHI T, YOSHIKAWA K. Time history nonlinear earthquake response analysis considering materials and geometrical nonlinearity [J]. Nuclear Engineering and Design, 2002, 212(1): 145-154.

[6]李忠献, 李忠诚, 梁万顺. 考虑地基岩土参数不确定性的核电厂结构随机地震反应分析 [J]. 核动力工程, 2006, 27(2): 30-35.

LI Z X, LI Z C, LIANG W S. Stochastic seismic response analysis for nuclear power plant structure considering parameter uncertainties of soil [J]. Nuclear Power Engineering, 2006, 27(2):30-35.

[7]朱秀云, 潘蓉, 李建波. 考虑SSI效应的核电站厂房楼层反应谱对比分析 [J]. 核技术, 2013, 36(4) : 50-57.

ZHU X Y, PAN R, LI J B. Comparison and analysis of the floor response spectrum of a nuclear power plant building considering the SSI effect [J]. Nuclear Techniques, 2013, 36(4):50-57.

[8]ROTARU I, SERBAN V, KRUTZIK N J, et al. Reanalysis and evaluation of the seismic capacity of the CANDU 700 MW NPP CERNAVODA [J]. Nuclear Engineering and Design, 2002, 212(1):381-393.

[9]NAKAMURA N, AKITA S, SUZUKI T, et al. Study of ultimate seismic response and fragility evaluation of nuclear power building using nonlinear three-dimensional finite element model [J]. Nuclear Engineering and Design, 2010, 240(1):166-180.

[10]刘燕军, 林皋, 李建波, 等. 计算核电厂楼层反应谱的直接法及其对比分析 [J]. 世界地震工程, 2011, 27(2):93-99.

LIU Y J, LIN H, LI J B, et al. A direct method and its comparative analysis for calculating the floor response spectrum of a nuclear power plant [J]. World Earthquake Engineering, 2011, 27(2):93-99.

[11]孟剑, 杨景龙. 安全壳极限承载力中预应力的数值模拟 [J]. 工业建筑, 2011(S1):127-131.

MENG J, YANG J L. Numerical simulation of prestress in the ultimate bearing capacity of the containment [J]. Industrial Construction, 2011, (S1):127-131.

[12]YONEZAWA K, IMOTO K, WATANABE Y, et al. Uitimate capacity analysis of 1/4 PCCV model subjected to internal pressure [J]. Nuclear Engineering & Design, 2002, 212(1-3):357-379.

[13]ZHANG C Y, CHEN P, ZHANG J H, et al. Evaluation of the structural integrity of the CPR1 000 PWR containment under steam explosion accidents [J]. Nuclear Engineering and Design, 2014, 278(1):632-643.

[14]聂建国, 王宇航. ABAQUS中混凝土本构模型用于模拟结构静力行为的比较研究 [J]. 工程力学, 2013, 30(4):59-67.

NIE J G, WANG Y H. Comparative study of concrete constitutive model to simulate static behavior of structures in ABAQUS [J]. Engineering Mechanics, 2013, 30(4):59-67.

[15]黄宗明, 白绍良, 赖明. 结构地震反应时程分析中的阻尼问题评述 [J]. 地震工程与工程振动, 1996, (2):95-105.

HUANG Z M, BAI S L, LAI M. A review of damping in structural seismic response time history analysis [J].Earthquake Engineering and Engineering Vibration, 1996(2):95-105.

[16]胡聿贤. 地震工程学 [M]. 北京：地震出版社.2006.

HU Y X. Earthquake Engineering[M]. Beijing: Seismological Press, 2006.

[17]曾奔, 周福霖, 徐忠根. 基于功率谱密度函数法的核电厂房增加隔震措施后的楼层反应谱分析 [J]. 核动力工程, 2009, 30(3):13-16.

ZENG B, ZHOU F L, XU Z G. Floor response spectra analysis of nuclear reactor buildings with additional base-isolation measures based on PSDF [J].Earthquake Engineering and Engineering Vibration, 2009, 30(3):13-16.