航向机动环境中基于陀螺/地磁信息融合的滚转角解算算法

张晓明,檀 杰,吕 辰,于天鹏,邱江涛

(1.中北大学 电子测试技术国防科技重点实验室,山西 太原 030051;2.中北大学 仪器科学与动态测试教育部重点实验室,山西 太原 030051;3.淮海工业集团有限公司,山西 长治 046012)

21世纪,随着灵巧弹药技术的迅猛发展,制导导弹逐渐成为国内外军事研究的热点。制导导弹制导化的核心是对滚转角的准确测量。传统的使用单一传感器如磁、陀螺等惯性器件作为滚转角测算单元的测试系统在弹体处于偏航角变化较大的复杂环境时,滚转角解算精度较差,不满足精度要求。因此,如何提高弹体在大偏航机动飞行环境中滚转角实时解算精度,成为制约导弹打击精度的瓶颈技术[1-2]。

磁传感器价格便宜,运用磁信息解算姿态角具有转速测量范围广,抗高过载,强自主性,并且误差不随时间累积等特点。目前磁测解算滚转角方法需要已知偏航为0,但弹体会在实际飞行过程中制导而航向机动,导致滚转角解算精度严重退化。而陀螺具备宽动态响应、抗震动、高效可靠、低成本、短时精度高等优点,但是单纯利用陀螺测量弹体轴向角速度,积分求解弹体滚转角存在误差随时间累积的不足。本文针对制导弹体机动飞行时传统方法采用地磁解算弹体滚转角精度下降的问题,提出一种轴向陀螺辅助三轴磁传感器的滚转角测试方案,将地磁解算的滚转角信息与陀螺短时积分的角度信息进行融合,提高弹体在航向机动环境中的滚转角解算精度。

1 基于陀螺/地磁的滚转角测量算法

1.1 硬件系统介绍

该测量系统主要由磁敏感单元、陀螺仪以及信号调理模块、MCU控制模块、电源模块组成。磁敏感单元采用HMC1043三轴磁阻传感器;陀螺仪采用ADXRS642单轴角速度陀螺仪;信号调理模块主要实现对三轴磁阻传感器微弱信号的放大、滤波以及单轴陀螺仪的带宽、量程设置[3];MCU控制模块主要完成对三轴磁阻传感器、单轴陀螺仪经过调理后的模拟信号的转换、磁干扰补偿、磁置复位电路所需PWM方波的产生和姿态解算,其主控芯片依靠STM32F405RGT6微控制器来实现;电源模块采用MIC5205稳压转换芯片提供所需供电电压。

1.2 滚转角测量原理

1.2.1 纯地磁滚转角测量原理

测量系统与弹体固联安装,磁传感器的三轴敏感方向与弹体坐标一致,通过预先计算地磁场在弹体发射系下的磁初始三分量Bn,以及在弹体机动飞行过程中弹体系下的三轴磁分量Bb,通过旋转矩阵公式:

Bb=CBn

(1)

就可以计算求出弹体的滚转角[4-5],其中,C为按一定顺序的3个方向余弦矩阵顺次乘积的矩阵形式,下标b,n分别代表弹体系和发射系;而其中3个姿态未知量,只有2个可以独立解算。因此,在非制导导弹中根据偏航角较小的运动规律假设偏航角为0,解算俯仰角和滚转角。这就是地磁解算滚转角的原理。然而制导导弹飞行过程包含自由飞行段和制导飞行段,在自由飞行段完全可以按照非制导导弹的假设解算滚转角;在制导飞行段弹体航向机动,不满足假设条件,不能假设偏航角为0,需要外加信息实时准确解算偏航角,进而才能准确解算弹体滚转角。

1.2.2 基于陀螺/地磁的滚转角测量原理

针对制导导弹制导飞行段航向机动的情况,在解算中加入陀螺信息。首先,将地磁解算提供的滚转角初值γm结合陀螺短时信息进行积分,求得一个高精度的滚转角信息γ′(γ′为融合了陀螺/地磁信息的滚转角值,为一个中间量);以γ′为已知量,利用旋转矩阵公式(1)递推求解下一时刻高精度的偏航角信息φs;以φs为已知量,通过式(1)即可推算得到下一时刻高精度的滚转角信息γs;而γs又作为当前时刻滚转角初值进行下一次的计算,重复此过程,便能得到每一个时间节点高精度的滚转角信息。具体步骤如图1所示。

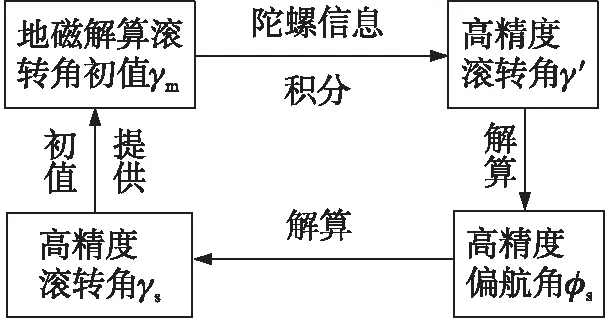
图1 基于陀螺/地磁信息融合的滚转角解算原理框图

1.3 坐标系的定义及坐标系转换

各坐标系如图2所示。地理坐标系Opxpypzp采用北东地坐标系,其原点定在地球表面运动物体的发射点上,Opxp指向北向,Opyp指向东向,Opzp垂直于xpOpyp平面且方向向下。

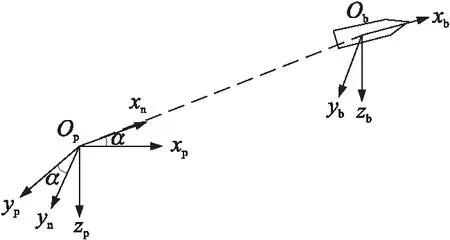
图2 坐标系

发射坐标系Opxnynzp。发射系原点位于载体上与载体固连,发射系不随载体转动。xnOpyn与xpOpyp处于同一平面内,Opzp轴垂直向下指向地心,与地理坐标系的Opzp轴重合;Opxn轴与Opyn轴由Opxp轴和Opyp轴各自绕Opzp轴旋转α角得到,α角则为弹体发射的航向角。

弹体坐标系Obxbybzb。弹体坐标系与弹体固连,随弹体转动,其原点位于弹体质心。Obxb轴与弹轴重合,方向指向弹轴前方;Obyb轴垂直于Obxb轴方向,向右为正;而Obzb轴垂直于xbObyb平面向下。

通过旋转矩阵公式Bb=CBn分析弹体系和发射系的关系,可得到关于滚转角γ、俯仰角θ和偏航角φ的旋转矩阵C:

(2)

1.4 滚转角解算方法

1.4.1 导弹自由飞行段

在导弹发射前,首先需要预先装载弹体发射系下的磁初始三分量,可根据当地的经纬度、海拔高度和弹体发射的航向角α,由IGRF模型和方向余弦矩阵求得,记为Bn=(Bn,xBn,yBn,z)T。而弹体在自由飞行过程中弹体系下的磁测三分量记为Bb=(Bb,xBb,yBb,z)T。由于制导导弹自由飞行段与非制导导弹的运动规律类似,故假设偏航角为0。将其代入旋转矩阵公式Bb=CBn中,即可得到磁初始三分量、磁测实时三轴分量与弹体姿态角之间的关系方程,解得俯仰角θm和滚转角γm:

(3)

式中:am=Bn,xsinθm+Bn,zcosθm。

1.4.2 导弹制导飞行段

当导弹过载恢复进入制导飞行段后,陀螺恢复使用,使用欧拉微分方程:

(4)

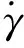
将Rx(γ)和Ry(θ)矩阵表达式代入式(4)得:

(5)

展开式(5),则

(6)

(7)

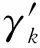
(8)

式中:a=Bn,xcosφk+1+Bn,ysinφk+1。

再利用所求得的偏航角φk+1和俯仰角θk+1求得k+1时刻高精度的滚转角γk+1:

(9)

式中:b=Bn,xsinθk+1cosφk+1+Bn,ysinθk+1sinφk+1+Bn,zcosθk+1,c=Bn,ycosφk+1-Bn,xsinφk+1。

以此类推,重复式(3)～式(9)的过程就能实时解算导弹制导飞行段每一时刻高精度滚转角[6-10]。

2 试验验证

针对上述方案进行了MATLAB仿真和系统试验验证,具体试验方案如下。

2.1 MATLAB仿真

为了模拟制导导弹飞行姿态,选用目前世界上公认的柔格里公式作为仿真模型:

(10)

式中:ωg为弹丸膛口自转角速率(单位:rad/s);A为修正系数;L为弹丸全长;D为弹径;J为弹丸极转动惯量;t为制导导弹飞行时间。

根据实际某型号弹,得到角速率变化模型:

ωx=34.89exp(-0.3t)

所以其飞行姿态设定如下:

①角速率的变化符合柔格里公式;

②俯仰角的变化是从40°～-40°,并且符合抛物线的变化趋势;

③偏航角的变化由制导导弹舵机控制,假定为正弦规律,变化幅度在+60°～-60°范围内。

仿真结果如图3～图5所示。

图3 仿真生成的地磁场信息

图5中,γm为纯地磁解算滚转角,γs为地磁陀螺信息融合解算滚转角,γb为滚转角仿真标准值。由图5求得,当纯地磁解算滚转角时,其滚转角误差均值为0.026 5°,标准差为1.395 1°;而当采用地磁和陀螺信息融合解算滚转角时,其滚转角误差均值为0.002 5°,标准差为0.032 3°。所采用融合算法有效消除了偏航角对解算姿态角的干扰,比纯地磁解算的误差减小一个数量级。

图4 仿真生成的陀螺角速率

图5 纯地磁和融合算法解算滚转角误差(仿真)的对比曲线

2.2 系统试验验证

把集成了HMC1043地磁传感器、ADXRS642角速度陀螺仪(2个传感器的测量精度均在1 mV以内)的系统捷联安装于转台上,如图6所示。

图6 三轴飞行仿真转台

在转台的0点位置上(内框、中框、外框均为0位置)预先装载初始三分量,上电内框在1 s内加速到5 r/s,外框在1 s内变到60°,之后内框以5 r/s的速度转动,中框和外框均按照60sin(2πt)的规律运动,此阶段20 s,实验全程共21 s。实验中三轴地磁信号和单轴陀螺信号如图7、图8所示。以三轴高速飞行仿真转台的反馈信息为基准信号,对比纯地磁解算和陀螺/地磁融合算法解算的滚转角误差,如图9所示。

由图7知,y轴、z轴地磁信号呈现正弦曲线变化,符合弹载环境下y轴、z轴磁场变化规律;x轴信号出现明显的波动,主要是由磁阻传感器的x轴与三轴高速飞行仿真转台的x轴不平行导致。图8为陀螺角速率信号曲线。图9为陀螺/地磁信息融合解算滚转角误差与纯地磁解算滚转角误差的对比曲线。从图9可以得出:纯地磁解算滚转角误差均值为-3.257 6°,标准差为2.977 1°;而当采用陀螺/地磁信息融合解算滚转角时,其滚转角误差均值为0.607 8°,标准差为2.249 5°。通过对比这2种算法结果可知,融合算法解算滚转角的误差均值减小为纯地磁解算的0.186 6,精度提高近6倍,而标准差也减小为纯地磁解算的0.755 6,并且消除了偏航对解算滚转角的干扰。

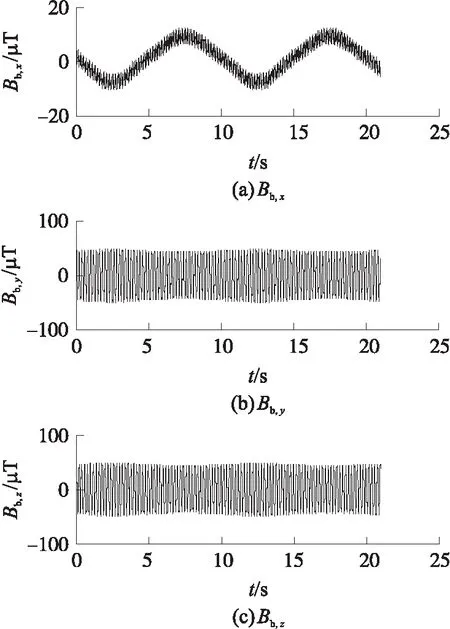
图7 三轴地磁信号

图8 陀螺角速率信号

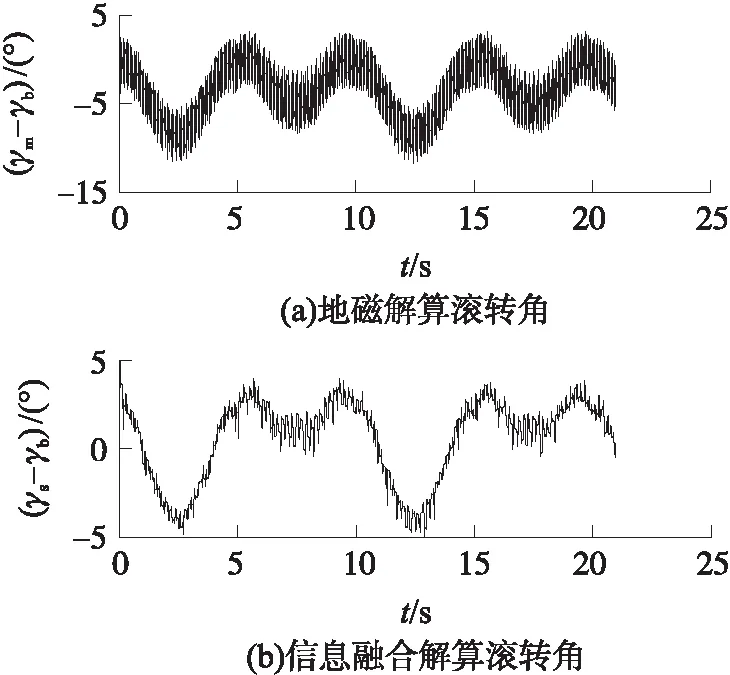
图9 纯地磁和融合算法解算滚转角误差(实验)的对比曲线

3 总结

本文提出了一种制导导弹大航向机动环境中应用的轴向陀螺辅助三轴地磁传感器的滚转角解算算法。该方法针对弹体旋转时其滚转角测量范围大,精度要求高,实现精确偏航打击等问题,利用三轴磁传感器信息和陀螺角速率信息融合的方法准确解算滚转角,弥补了单一磁传感器在弹体机动飞行、偏航角变化大的环境中解算滚转角精度较差的缺点,通过MATLAB仿真对比了2种算法的精度。系统转台试验结果表明,此滚转角测量方法提高了滚转角测算精度,能够很好地将滚转角解算精度控制在5°以内,提高了系统的抗机动干扰能力,在制导导弹精确偏航打击上具有可行性。

[1] 孙明玮. 21世纪对精确打击弹药制导技术的需求[J]. 飞航导弹,2006(2):49-59.

SUN Mingwei. Demand for accurately attacking ammunition guidance techniques in the 21st century[J]. Aerodynamic Missiles Journal,2006(2):49-59. (in Chinese)

[2] 黄晓霞,李荣强,张艳霞. 信息化弹药的研究现状及发展建议[J]. 兵工自动化,2008,27(4):56-58.

HUANG Xiaoxia,LI Rongqiang,ZHANG Yanxia. Status and suggestions of development of information ammunition[J]. Ordnace Industry Automation,2008,27(4):56-58. (in Chinese)

[3] 赵鑫炉,张晓明,龙达峰,等. 旋转弹用滚转角磁测系统设计[J]. 传感技术学报,2013,26(9):1 309-1 313.

ZHAO Xinlu,ZHANG Xiaoming,LONG Dafeng,et al. The design of roll angle magnetic measurement system used in spinning projectiles[J]. Chinese Journal of Sensors and Actuators,2013,26(9):1 309-1 313. (in Chinese)

[4] 龙达峰,刘俊,张晓明,等. 高速旋转弹飞行姿态磁测解算方法[J]. 弹道学报,2013,25(2):69-73.

LONG Dafeng,LIU Jun,ZHANG Xiaoming,et al. Magnetic survey solution method for flying attitude of high-speed rotating ammunition[J]. Journal of Ballistics,2013,25(2):69-73. (in Chinese)

[5] 张晓明,王天宇,关洋,等. 常规弹药滚转角磁测算法中偏航角干扰分析[J]. 测控技术,2016,35(10):116-119.

ZHANG Xiaoming,WANG Tianyu,GUAN Yang,et al. Interference analysis of yaw in rotation angle algorithm of conventional ammunition based on geomagnetic information[J]. Measurement & Control Technology,2016,35(10):116-119. (in Chinese)

[6] 曹红松,冯顺山,赵捍东,等. 地磁陀螺组合弹药姿态探测技术研究[J]. 弹箭与制导学报,2006,26(3):142-145.

CAO Hongsong,FENG Shunshan,ZHAO Handong,et al. Researching ammunition attitude detect technique combination of geomagnetism and gyro[J]. Journal of Projectiles,Rockets,Missiles and Guidance,2006,26(3):142-145. (in Chinese)

[7] 代刚,李枚,苏伟,等. 自旋导弹捷联式陀螺/地磁姿态测量方法[J]. 中国惯性技术学报,2010,18(6):702-705.

DAI Gang,LI Mei,SU Wei,et al. Strapdown gyroscope/magnetometer attitude measurement method for spinning missile[J]. Journal of Chinese Inertial Technology,2010,18(6):702-705. (in Chinese)

[8] 韩艳. 制导炮弹飞行姿态的陀螺/磁阻传感器组合测量方法研究[D]. 南京:南京理工大学,2010.

HAN Yan. Investigation on combined measurement of guided projectile’s attitudes based on gyro/magnetometer[D]. Nanjing:Nanjing University of Science and Technology,2010. (in Chinese)

[9] 李永慧. 基于磁阻传感器的常规弹姿态测量技术研究[D]. 太原:中北大学,2012.

LI Yonghui. Research of attitude determination technology based on magneto-resistive sensor for conventional ammunition[D]. Taiyuan:North University of China,2012. (in Chinese)

[10] 王嘉雨. 地磁/陀螺信息融合的姿态解算算法研究[D]. 太原:中北大学,2015.

WANG Jiayu. Investigation on geomagnetic/gyro attitude algorithm method of information fusion[D]. Taiyuan:North University of China,2015. (in Chinese)