概率积分法沉陷预计与参数反演优化算法及实现

薄怀志，宋炳忠，李川建，王猛，卢国宏，陈宗成，李云伟

(1.山东省地质矿产勘查开发局第三水文地质工程地质大队，山东 兖州 272100；2.山东省地质矿产勘查开发局第二地质大队，山东 兖州 272100；3.山东省地矿局采煤塌陷地综合治理工程技术研究中心，山东 兖州 272100；4.武汉大学 测绘学院， 湖北 武汉 430000)

0 引言

目前概率积分法沉陷预计在“三下采煤”、矿区土地复垦、采煤塌陷地治理规划设计、矿区建筑物稳定性评估等工作中应用广泛[1-4]。近年来，对任意多边形的沉陷预计研究较多，吴侃[5]首先将非矩形工作面划分为若干小矩形工作面，分别进行预计，然后将各个小矩形预计结果叠加的方法；许冬等[6]将任意多边形工作面按照角点划分为若干梯形，分别预计后叠加(减)处理实现沉陷预计；徐孟强等[7]提出了利用三角剖分根据角点将多边形工作面划分为若干三角形、分别预计后对各三角形预计结果叠加(减)的方法。可以看出，对于任意多边形开采区域划分多从角点往内进行剖分，容易造成小的剖分区域重复计算或遗漏，难以真正实现任意多变形开采区域沉陷预计。概率积分法预计参数反演常用模矢法和遗传算法。模矢法是传统的直接寻优算法的典型代表，但该算法对初值可靠性要求较高，初值选取不当，求参结果易陷入局部极值[8-9]。遗传算法是典型的智能算法，但算法求解有一定的不稳定性，即使求参数据完全相同，每次求参结果都会有一定的差异，且算法执行效率低、后期收敛慢[10-11]。

该文提出了使用Delaunay三角剖分方法，将任意多边形开采区域划分为若干三角形，然后对三角形区域进行沉陷预计，累加得到总沉陷值的方法，解决了任意多边形沉陷预计的难题。综合模矢法和遗传算法优点，提出了组合算法，提高了概率积分法参数反演精度和效率，开发了集实测数据处理、预计模型参数反演和移动变形预计三大模块于一体的地表移动变形数据处理软件。

1 基于用Delaunay三角剖分的沉陷预计方法

1.1 概率积分法简介

概率积分法是以随机介质理论为基础，以正态分布为影响函数，用积分式描述下沉盆地的方法，因其预计公式中包括概率积分计算而得名[12]。概率积分法预计计算公式如下：

下沉：

水平移动：

式中：W(x,y)为地表任意点的下沉值(mm)；Ux(x,y)为走向方向的水平移动值(mm)；Uy(x,y)为倾斜方向的水平移动值(mm)；Wem，Uem为充分采动时地表最大下沉值和最大水平移动值(mm)；r为走向主断面上采空区边界(m)；μ,λ分别为x,y方向的变形值(mm)；x,y为计算点相对坐标；D为开采煤层区域。

1.2 技术路线

基于用Delaunay三角剖分的概率积分法，沉陷预计算法流程如下：

(1)对于任意多边形工作面进行Delaunay三角形剖分。

(2)计算每一小三角单元的开采对地表点P的下沉影响理论值。

(3)判断每一小三角单元距离煤壁的距离，根据距离和该小三角形开采区域的采深，将乘以一个影响系数ρ(ρ≤1)，获得该小三角形区域开采对P点的实际下沉影响值。

(4)对各小三角单元开采影响进行叠加，求得开采引起的P点的沉降量。

(5)汇总计算得到预计区域的沉陷值。

1.3 Delaunay三角剖分

Delaunay三角剖分具有以下特性：①最接近：以最近的三点形成三角形，各边皆不相交；②唯一性：从任何位置开始构建，剖分结果均相同；③最优性：任意两个相邻三角形组成的凸四边形对角线互换，内角中最小角不会变大；④区域性：新增、删除、移动某一个顶点时只会影响临近的三角形[13]。Delaunay三角剖分可以最大限度地避免狭长三角形的产生，采用Delaunay三角剖分，对任意多边形开采区域进行剖分非常合适。

首先对开采区域进行插点，插点距离为预计范围最短边长的1/10，且不小于20m时能够获得比较好的效果。对开采区域插点完毕后，即可使用三角网生长算法来对开采区域进行三角剖分，三角网生长算法构网的实现过程如图1所示。

图1 Delaunay三角形剖分算法构网过程

该算法对凸多边形和凹多边形剖分结果如图2所示，可以看出，该种算法剖分的多边形区域单元三角格网比较规则，没有出现狭长边。

图2 任意多边形的Delaunay三角剖分

1.4 单元三角区域引起地面沉陷计算

Delaunay三角剖分后，计算每一个小三角区域的开采对地表点P的影响，叠加即可得到开采区域对地表点P的下沉影响。由于单元三角形的范围较小，可以将单元区域的煤层视为水平煤层来计算单元区域开采对P点的影响。

图3 单元三角网格开采沉陷影响计算示意图

如图3所示，以△OAB的最长边为x轴，建立如图所示的局部坐标系，设O点位原点，A点坐标为(x2,0)，B点坐标为(x1，y1)。则OB，AB的直线方程可表示为：

采用先积分μ再积分λ进行计算，公式为：

由于单元三角区域较小，开采影响半径r可以采用单元三角中心点的采深进行计算。令：

使用无穷级数将幂级数展开至二次项，则有：

将幂指数积分转换为二元二次函数积分，通过变量替换，可以相对简单对上式进行二次积分。

1.5 单元开采区域影响系数ρ的计算

改进的算法可以实现任意多边形开采的工作面沉陷预计，由于顶板的悬臂作用，距离开采边界越近的单元，区域顶板下沉量越小，当超过开采边界一定距离后，顶板才能到达最大下沉量。需要引入一个修正系数，对单元三角区域下沉值进行修正。三角单元开采引起地表点实际沉降量与该单元距离采空区边界的距离成正比，不同采深的三角单元开采对地面的影响也不同，这种性质与Maxwell-Boltzmann分布的积分函数变化形态非常相似(图4)[14]。

图4 Maxwell-Boltzmann分布函数的积分函数图像

三角单元影响系数ρ可使用该函数表达：

式中：x为三角单元至采空区的距离；a为与采矿地质条件有关的系数。

2 改进的概率积分法参数反演方法

2.1 常用概率积分法参数反演方法简介

目前开采沉陷预计时多使用概率积分法，初期概率积分法参数反演多使用线性近似法，后逐步发展到实验设计法和智能算法[15]。模矢法是直接寻优算法的典型代表，应用广泛，但该算法对初值可靠性要求较高，初值选取不当求参结果易陷入局部极值[16]。近年来，概率积分法参数反演智能算法发展迅速，典型代表有遗传算法[10]、神经网络算法[17]、退火算法[18]、果蝇算法[19]、随机粒子群算法[20]等，其中遗传算法是智能算法的典型代表。

模矢法又称为步长加速法，是求取非线性无约束最优解问题的算法。模矢法将待求参数看作一组矢量，通过改变寻优方向和步长寻找一组最优参数，具有方便计算机编程和加速向最优点移动的优点，且可根据任意形状工作面的实测地表移动观测数据进行概率积分法参数求取。遗传算法是一种通过模拟自然进化过程来搜索最优解的方法，通过编码将求解参数解映射为种群个体的染色体，使用交叉、变异算子维持种群的多样性，使用选择算子使种群向最优方向进化。遗传算法具有隐含的并行搜索能力，能够使求解参数跨过局部极值的障碍向全局最优值进化。

2.2 组合算法

首先利用遗传算法的全局寻优能力求得全局近似最优参数，然后将近似最优参数适当取舍后作为模矢法探索的起点，最后利用模矢法的局部探索能力来获得预计参数的精确解，具体步骤为：①使用遗传算法反演得到预计参数的全局近似最优值；②取近似最优值小数点后一位作为初始模矢点的参数值；③使用模矢法反演出精确的最优参数，具体流程如图5所示。

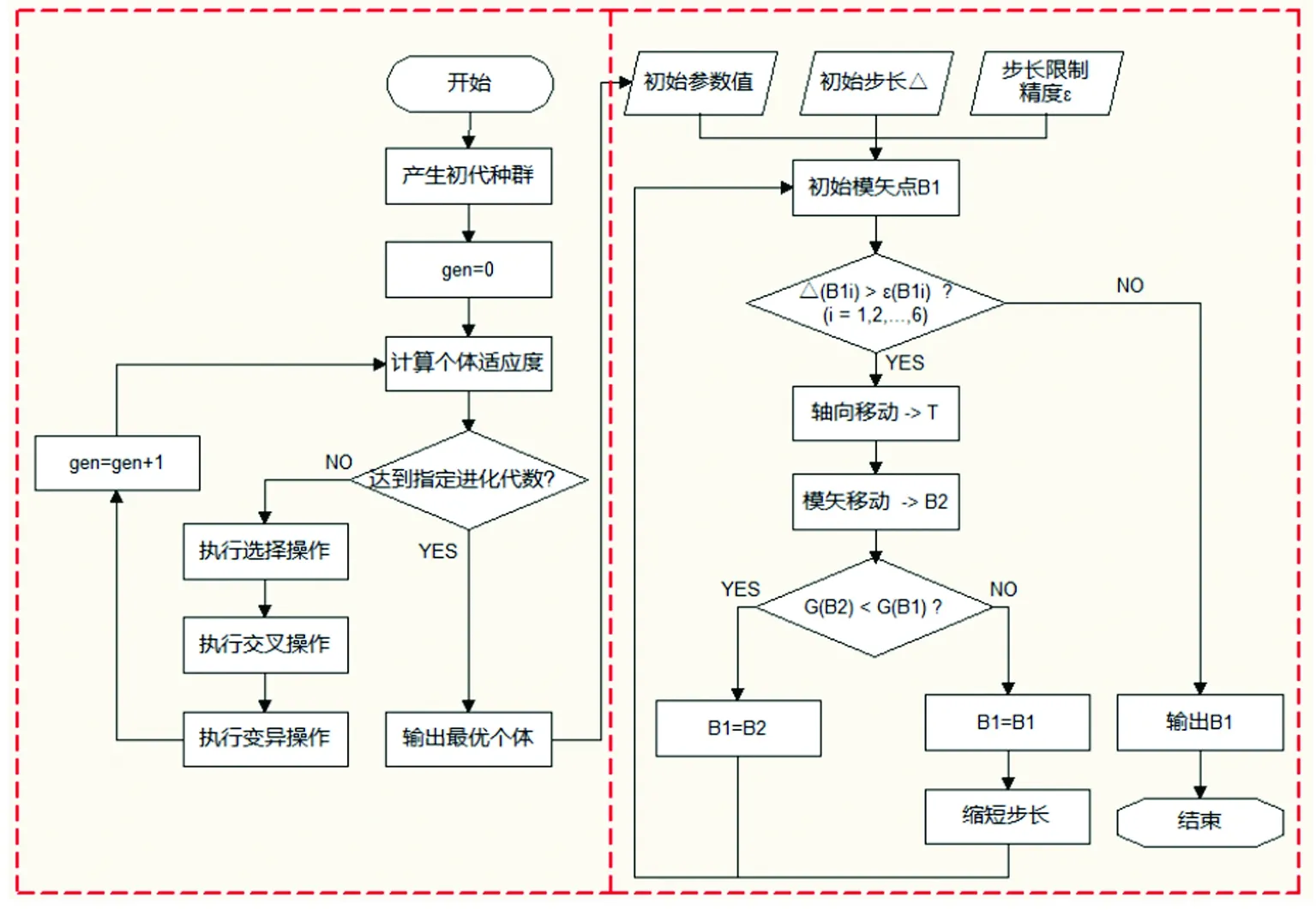
图5 组合算法流程图

3 系统实现

3.1 系统简介

按照改进的概率积分法算法，开发了地表移动变形数据处理软件。使用C#语言开发的基于Autocad.net的插件，可以加载在Autocad2006及以上的CAD版本中(图6)。软件纵向采用了分层设计的思想，开采沉陷数据处理与预计软件纵向结构分为用户交互层和数据处理层。横向采用了模块化设计思想，主要包括实测数据处理模块、移动变形预计模块和最优参数反演模块。

图6 软件主界面

3.2 系统主要功能模块

3.2.1 实测数据处理模块

将Excel格式的沉降、水平移动观测数据导入软件后，使用数据处理功能处理即可以直接绘制地表沉降过程中的各种动态变形曲线图。

可以根据实测数据求取超前影响距(角)与滞后距(角)等动态地表移动变形参数和边界角、移动角、地表移动变形持续时间、移动变形最大值等稳态地表移动变形参数。

3.2.2 最优参数反演模块

软件提供模矢法和遗传算法两种概率积分法最优参数反演方法，既可使用单一方法求参，也可以使用组合方法。如果没有可供参考的相邻采区或类似地质采矿条件下的预计参数作为反演初值，不宜采用模矢法进行求参。而遗传算法、组合算法则基本不受这种因素的影响，但是从算法的准确性和效率方面来说，组合算法又优于遗传算法，该算法比较适用于没有相关预计参数可供参考情况下的概率积分法预计参数反演。软件可以以观测数据的时间为依据，进行动态或静态求参(图7、图8)。

图7 沉降动态求参结果图

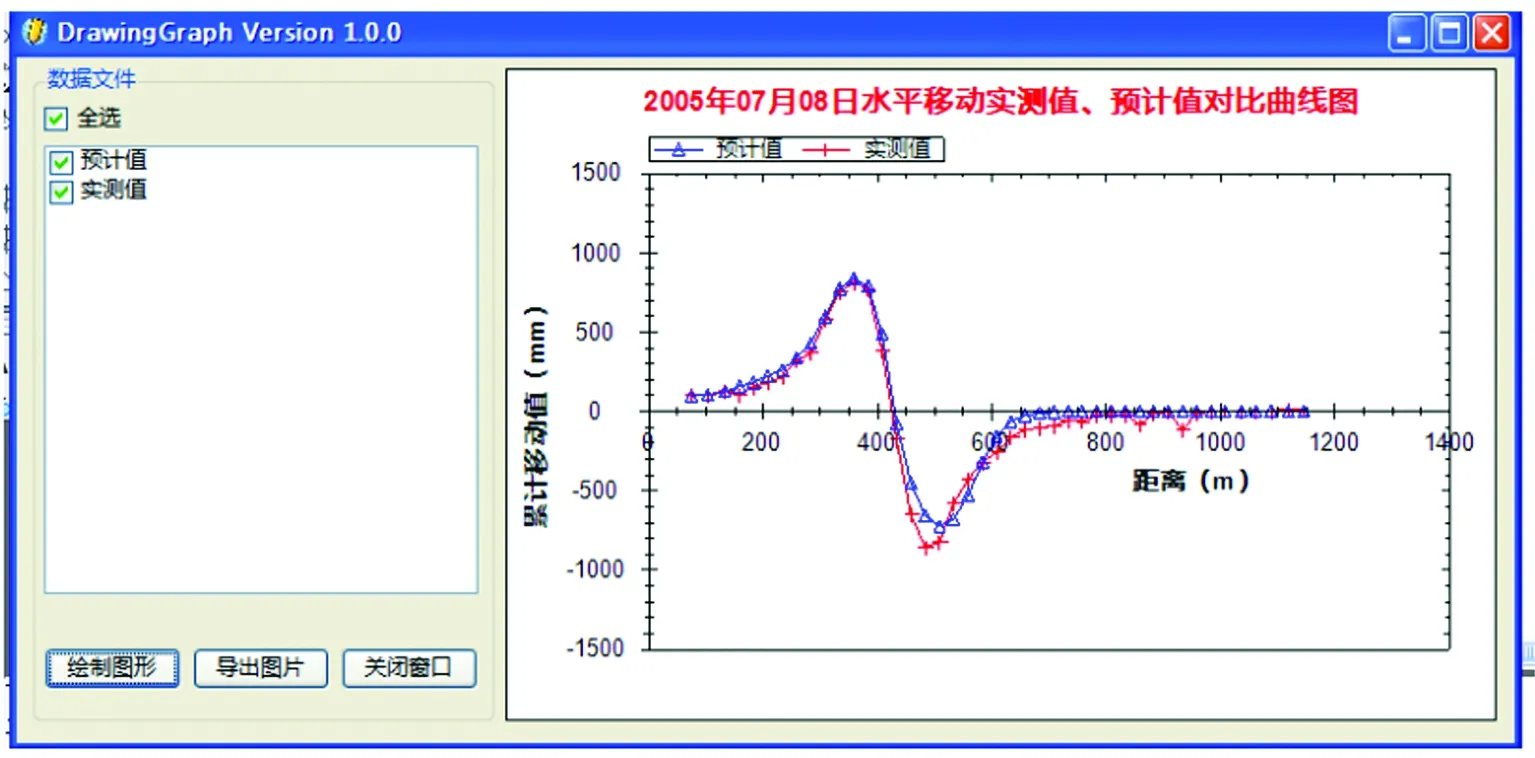
图8 水平移动动态求参结果图

3.2.3 变形预计模块

基于Delaunay三角剖分算法开发了地表移动变形预计模块，实现了任意多边形工作面沉陷预测，输出预计结果、各类等值线图及三维沉陷模型，并可以通过旋转从多角度查看三维模型(图9、图10)。

图9 等沉陷曲线图

图10 沉陷三维模型图

4 结论

(1)开采沉陷数据处理与预计软件开采区域使用Delaunay三角剖分，由于Delaunay三角剖分具有最接近性、唯一性、最优性、最规则、区域性的特点，适合用于不规则任意多边形采煤沉陷预测，真正实现了任意形状工作面的地表移动变形预计。传统的概率积分法根据拐点偏移距确定计算范围，认为拐点偏移距至煤壁的距离上覆煤层都是假设不发生下沉的。该算法使用Maxwell-Boltzmann函数，每个剖分三角单元的沉陷影响系数ρ(ρ≤1)，来解决传统概率积分法拐点偏移距引起的误差。

(2)将遗传算法和模矢法用于概率积分法预计模型的最优参数反演，优劣互补，充分发挥两者的优点。如果矿区有比较可靠的参数参考值，直接以该参考值作为初值使用模矢法进行解算，节省解算时间。如果矿区没有可靠参数值，可以给参数值设定一个范围，使用遗传算法解算概率积分法最优参数值。也可以将模矢法、遗传算法进行融合，首先利用遗传算法的全局寻优能力求得全局近似最优参数，然后将近似最优参数适当取舍后作为模矢法探索的起点，最后利用模矢法的局部探索能力来获得预计参数的精确解。

(3)开发了集实测数据处理、最优参数反演、采煤沉陷预计三大模块于一体的开采沉陷数据处理与预计软件，即可处理矿山岩移观测数据，绘制各类变形曲线图，也可实现概率积分法最优参数反演和采煤沉陷预测。

[1] 赵博,李爱军,刘术明．昭阳煤矿矿山地质环境影响评估及监测建议[J].山东国土资源,2017,33(5):35-41.

[2] 隋建红.山东省黄河北煤炭矿区地表沉陷预测与综合治理研究[J].山东国土资源,2017,33(3):59-63.

[3] 孔凡杜.滕县煤矿区矿山地质环境综合评价研究[J].山东国土资源,2017,33(1):59-64.

[4] 隋建红,郝启勇.山东省黄河北煤炭矿区地质环境承载力评价[J].山东国土资源,2017,33(4):34-40.

[5] 吴侃，葛家新，王玲丁，等．开采沉陷预计一体化方法[M]．徐州:中国矿业大学出版社，1998：1-20.

[6] 许冬，王临清，吴侃．任意形状工作面沉陷预计计算方法[J]．金属矿山，2014(5):55-59．

[7] 徐孟强,查剑锋.基于三角形剖分算法的开采沉陷预计系统设计[J].金属矿山,2016(2):128-131.

[8] 朱晓峻,郭广礼,方齐.概率积分法预计参数反演方法研究进展[J].金属矿山,2015(4):173-177.

[9] 冉典,吴捷.模矢法在厚松散层地表移动参数解算中的应用[J].地矿测绘,2014(2):25-27.

[10] 查剑锋,冯文凯,朱晓峻.基于遗传算法的概率积分法预计参数反演[J].采矿与安全工程学报,2011,28(4):655-659.

[11] 潘国荣，谷川.改进的遗传算法用于工业测量数据处理[J].大地测量与地球动力学，2008，28(1)：55-58.

[12] 国家煤炭工业局．建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规程[S].北京:煤炭工业出版社，2004.

[13] 刘建耀,刘保顺.基于C#和AutoCAD的Delaunay三角剖分算法的实现[J].有色矿冶,2014,30(5):9-14.

[14] 陈永良，周斌，李学斌.基于Boltzmann机的矿产靶区预测[J].地球物理学进展,2012,27(1):179-185．

[15] 朱晓峻,郭广礼,方齐.概率积分法预计参数反演方法研究进展[J].金属矿山,2015(4):173-177.

[16] 刘宝琛,戴华阳.概率积分法的由来与研究进展[J].煤矿开采,2016(2):1-3.

[17] 郭文兵,邓喀中,邹友峰.概率积分法预计参数选取的神经网络模型[J].中国矿业大学学报,2004(3):88-92.

[18] 苏军明,朱建军,伍雅晴,等.模拟退火算法在概率积分法参数反演中的应用[J].工程勘察,2015(12):76-79.

[19] 陈涛,郭广礼,朱晓峻,等.利用果蝇算法反演概率积分法开采沉陷预计参数[J].金属矿山,2016(6):185-188.

[20] 王正帅,邓喀中,康建荣.概率积分法参数反演的文化-随机粒子群优化算法[J].辽宁工程技术大学学报(自然科学版),2013(3):311-315.