基于模拟退火的交叉口自适应信号控制优化研究

曹 阳

（西南交通大学，交通运输与物流学院，成都610031）

0 引 言

信号交叉口作为城市网络中不同道路相互接驳的节点，是不同方向的交通流聚集并疏散的重要交通设施。不合理的信号控制势必会增加道路通行车辆的延误时间，甚至可能对路网相邻的其他节点产生负面影响，从而诱发更加严重的交通拥堵。随着交通科学技术的发展，交通信号控制由定时信号控制发展为自适应信号控制，控制范围也历经了单点控制、干线控制以及区域控制三个阶段。

国内外学者对信号控制方法和模型开展了广泛的研究。在最早期的信号控制研究中，Webster以车辆平均延误最小为目标建立了信号配时模型，该方法计算过程简单易懂，在实际工程中得到了广泛的应用。在Webster算法的基础上，衍生出了许多的模型和算法来解决不同交通条件下交叉口信号控制问题。其中，一部分学者提出了以解析方法为手段的数学模型[1-3]，此类方法通过应用排队论的理论模型，并借助人工操作经验从而实现交叉口的信号控制，在城市交通需求波动的复杂性和动态性条件下适用性不强。而随着启发式算法的快速发展，越来越多基于启发式算法的配时优化模型也开始运用在城市交通问题中，但研究中也存在一定的局限性。文献[4]采用分布式控制技术来解决信号控制问题，提出了基于神经网络的实时交通信号控制模型，但过于繁杂的控制会显著增加系统的负担，导致系统处于振荡的状态。还有学者利用遗传算法对信号控制进行优化，文献[5]通过遗传算法求解了交叉口信号优化双层规划模型，但仅适用于固定信号配时，且易陷入局部最优解。文献[6-7]基于遗传算法对交叉口交通流建立了动态信号配时模型，但信号控制方案并未考虑特定周期到达的车流量，在短期车流变化大的情况下将无法适用。黄艳国在单路口Agent中引入加强学习方法，通过交通信号实时在线调整来减少车辆的延误，但仿真结果表明在饱和流量下协调算法作用不明显[8]。张存保等在车路协同环境下设计了单点交叉口信号控制优化的流程，降低交叉口的延误和停车次数[9-10]，但最小最大绿灯时间为经验所给的定值，不能反映现实交通流突变导致相位约束的合理性。

综上所述，目前充分考虑交叉口各进口道车流短时到达情况并减少算法复杂度的研究相对较少。本文旨在合理估计短时交通流，进而结合高效算法准确优化信号配时，主要以单点信号交叉口为对象，利用神经网络模型准确预测各进口短期时间窗交通流到达。在此基础上，以平均延误最小作为优化目标构建单目标规划模型，并利用易于实现与应用的模拟退火算法快速寻找全局最优解。最终通过优化信号配时方案缩短交叉口整体延误时间，提高交叉口的服务水平。

1 交通流预测模型

目前，我国城市交叉口主要采用固定信号周期控制的方法，即交叉口按照预先设定好的控制方案运行，属于车流单向适应信号的范畴。但交叉口车流量往往具有一定的动态波动性，定时控制不能完全适应和满足短期交通需求的变化。在车联网环境下，交通管理者能够依据各进口车道历史车流量信息来预测短期交通流到达，从而制定相应的控制策略来适应交通流变化规律，最大化的利用交叉口通行能力。

为了掌握交叉口各进口车流到达的交通需求，需要通过一定方法来进行短期交通流的预测。本文考虑了具有初步的自适应与自组织能力的BP（Back Propagation，后向传播）神经网络模型，在学习或训练过程中改变突触权重值，以适应周围环境的要求。BP神经网络能够较容易地描述非线性时间序列联系，具备泛化以及容错的能力，因此可以适用于交叉口交通流动态预测问题。BP神经网络包括输入层、隐含层和输出层，逻辑拓扑结构见图1所示。

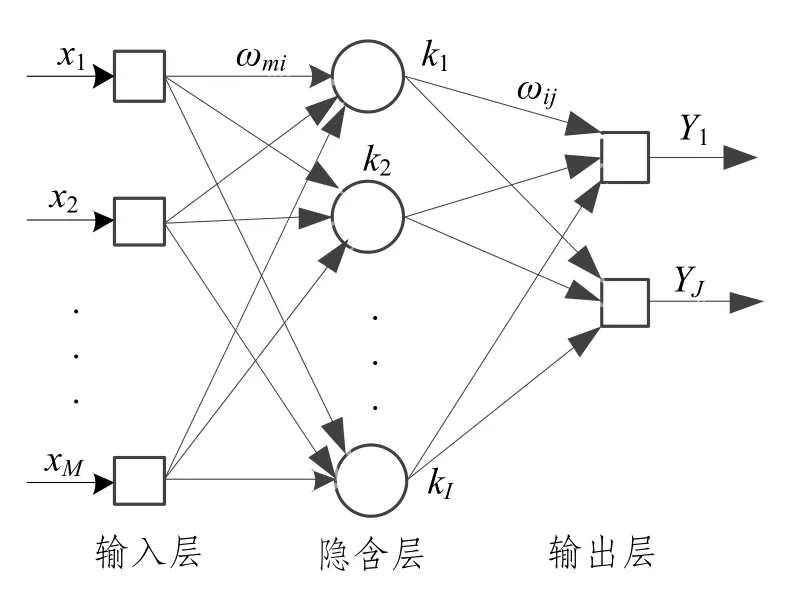
图1 BP神经网络的逻辑拓扑结构图Fig.1 Topology structure of the BP neural network

图1中，xi为神经网络的输入，输入节点数为M；ωmi为输入层和隐含层之间的连接权值；ki为隐含层结果，节点数为I；ωij为隐含层和输出层之间的连接权值；Yi为输出层结果，节点数为J。

本文中的输入样本为各个进口的历史交通流量数据，由分布于进口道上游的数据采集器采集得到。将相邻的15组流量数据作为一个样本输入，即M=15，利用BP神经网络预测下一个周期各进口道流量，具体步骤如下：

步骤1 统计单个周期内相位i进口道j的车流量qij，将样本数据进行归一化处理，归一化公式为：

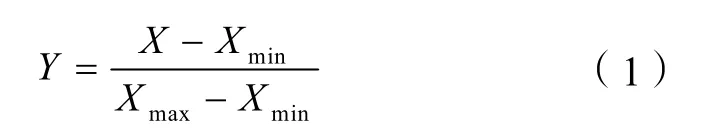
式中，X为流量样本数据；Xmin为流量样本中的极小值；Xmax为流量样本中的极大值；Y为流量样本标准化的值。

步骤2 建立BP神经网络模型并训练该网络。随机初始化各层之间的连接权值ωmi和ωij，确定输入层节点个数M为15，输出层节点个数J为1，隐含层的节点个数参照下式：

式中，a为[1，10]之间整数，按经验取3。

步骤3 通过反馈误差不断训练修正连接权值，最终得到最佳的网络。进而利用训练好的网络预测下一周期交通流Y*，反归一化处理还原短期交通流的预测值q*ij，公式如下：

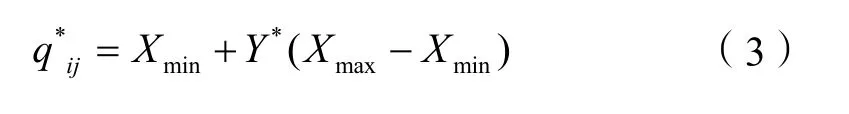
2 动态配时优化模型

交通信号控制的目的在于时序上将冲突交通流从空间上隔开，从而使得冲突交通流安全地通过交叉口继续开往下游。而交叉口平均车辆延误能够反映其被利用的效率，是作为评判交叉口服务水平的重要尺度。近年来，车联网技术发展速度迅猛，能够通过车车、车路信息交互获取车辆和道路的信息，整合道路信息资源，达到缓解道路拥堵的目标。因此，本文以通过交叉口的车辆平均延误最小为目标，对各相位的绿灯时间进行优化，通过确定信号周期内最优化的绿灯时间，实现目标最优。

2.1 平均延误

车辆延误由均匀延误和随机延误组成，均匀延误可通过排队轨迹时空图推导，而随机延误可以用排队论来描述。车辆到达流率服从均值为q的泊松分布，进口道车队的驶出率为s，用M/D/1排队模型描述相位i下进口车道j的车辆平均延误dij为：

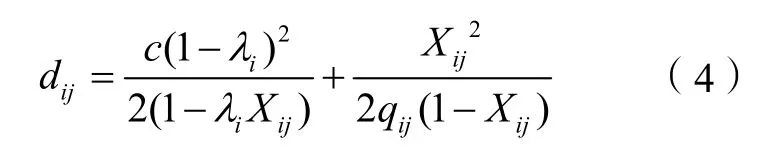
式中，c为信号周期总时长；λi为相位i的绿信比；Xij为相位i进口道j的饱和度。

由式（4）可知，dij能根据进口车流的大小及分配的绿灯时间来确定。因此，交叉口所有车辆的平均延误d为交叉口所有进口道的车辆平均延误与车流量乘积的加权平均，即：

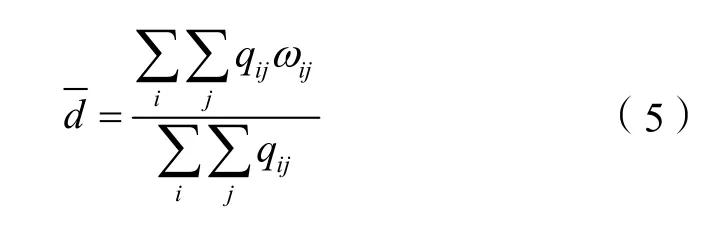
2.2 最小绿灯时间

为了保证各个相位具有最小的通行时间，降低交通流预测误差对信号控制的影响，应该设置最小绿灯时间保证基本的通行量。美国《交通信号设计手册》推荐的根据检测器位置确定的最小绿灯时间如表1：

表1 最小绿灯时间和检测器位置参考值Tab.1 Suggested values of minimum green time and detector position

根据表1可以获得各个进口方向的最小绿灯参考值，相位i的最小绿灯推荐值应取各进口车道时间参考值的最大值：

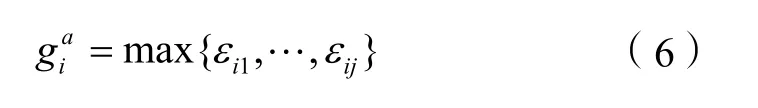
式中，εij为相位i进口道j的最小绿灯参考值。

最小绿灯推荐值是根据大量交叉口信号控制经验得来的，而交通流在每一周期内的到达具有随机性，完全根据此推荐值来确定最小绿灯时间不能反映车流随机到达和初始排队的特性。在自适应控制中，可以根据各进口车道的初始车辆状态来确定初始绿灯时间goi。其计算公式为：

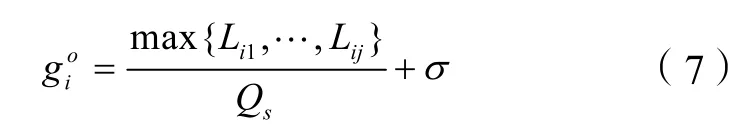
式中，Lij为相位i进口道j的初始排队车辆数；Qs为进口道饱和流率；σ为车辆启动损失时间（一般为3s）。

当初始排队较短时，初始绿灯时间将较小，此时应该将最小绿灯推荐值gia作为最小绿灯时间；相反则应该将初始绿灯时间go作为最小绿灯i时间。因此，相位i的最小绿灯时间gimin的计算公式为：

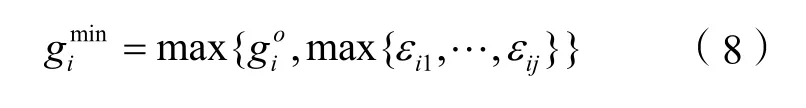
2.3 最大绿灯时间

最大绿灯时间是为了保持最佳绿信比分配而确定的相位绿灯时间，当相位车流量很大时能够满足绿灯时间的延长。当绿灯时间达到最大绿灯时间，能够强制转换相位从而均衡各相位绿灯时间。因此相位的最大绿灯时间大于最小绿灯时间，并且小于周期有效绿灯总时间。

2.4 自适应动态配时模型

本文将交叉口所有车辆的平均延误最小作为优化目标，从而最大化地利用道路资源，提高交叉口通行能力。因此目标函数为：

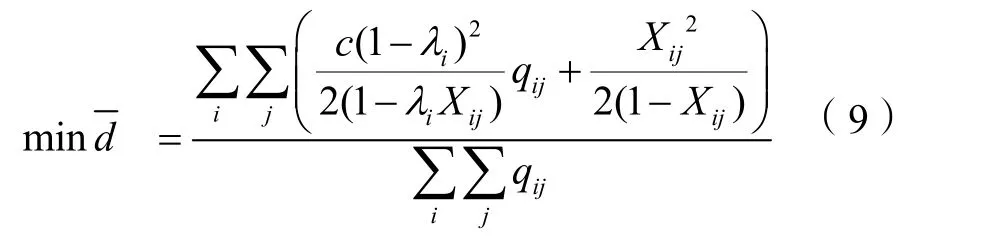
约束条件为：

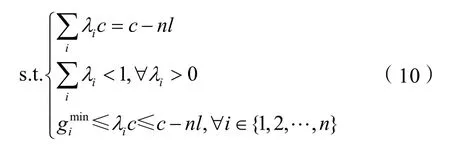
约束条件中，n为交叉口设计的相位数；l为相位损失时间。

3 模拟退火的交通配时优化

模拟退火算法是基于蒙特卡洛迭代求解策略的一种随机寻优方法。在解决局部最优和全局最优问题上具有突出表现。其本质是借鉴固体的物理退火过程，随着固体温度不断降低，逐渐平衡并达到基态，从而收敛到全局最优解。在本文中，借助该最优化方法求解交叉口延误最小时的信号控制方案，从而提高交叉口服务水平。

基于模拟退火的交叉口信号控制方案寻优算法步骤如下：

步骤1 设定初始化冷却进度表参数：初始温度T0，衰减函数f(T)，以及马尔科夫链长度L。

步骤2 根据各相位关键车道车流量比例，按照均匀分配方式确定初始相位绿信比初始解λ={λ1,…,λn}作为当前解，交叉口平均延误为(λ)。

步骤3 设计随机扰动rand产生新解空间λ′={λ1+rand1,…,λn+randn}，交叉口平均延误为(λ')。

步骤4 如果(λ′)≥(λ)，进入步骤5；若(λ′)＜(λ)，则接受新解λ′作为当前解，进入步骤6。

步骤5 产生一个(0,1)之间的随机数η，若eϖ(λ)-ϖ(λ')＞η则将新解λ′作为当前解；否则仍将原解λ作为当前解。

步骤6 进行退火，即Tk+1=f(Tk)；若满足温度下降终止条件Tk≤Tmin，则进入步骤7；若不满足则转至步骤3。

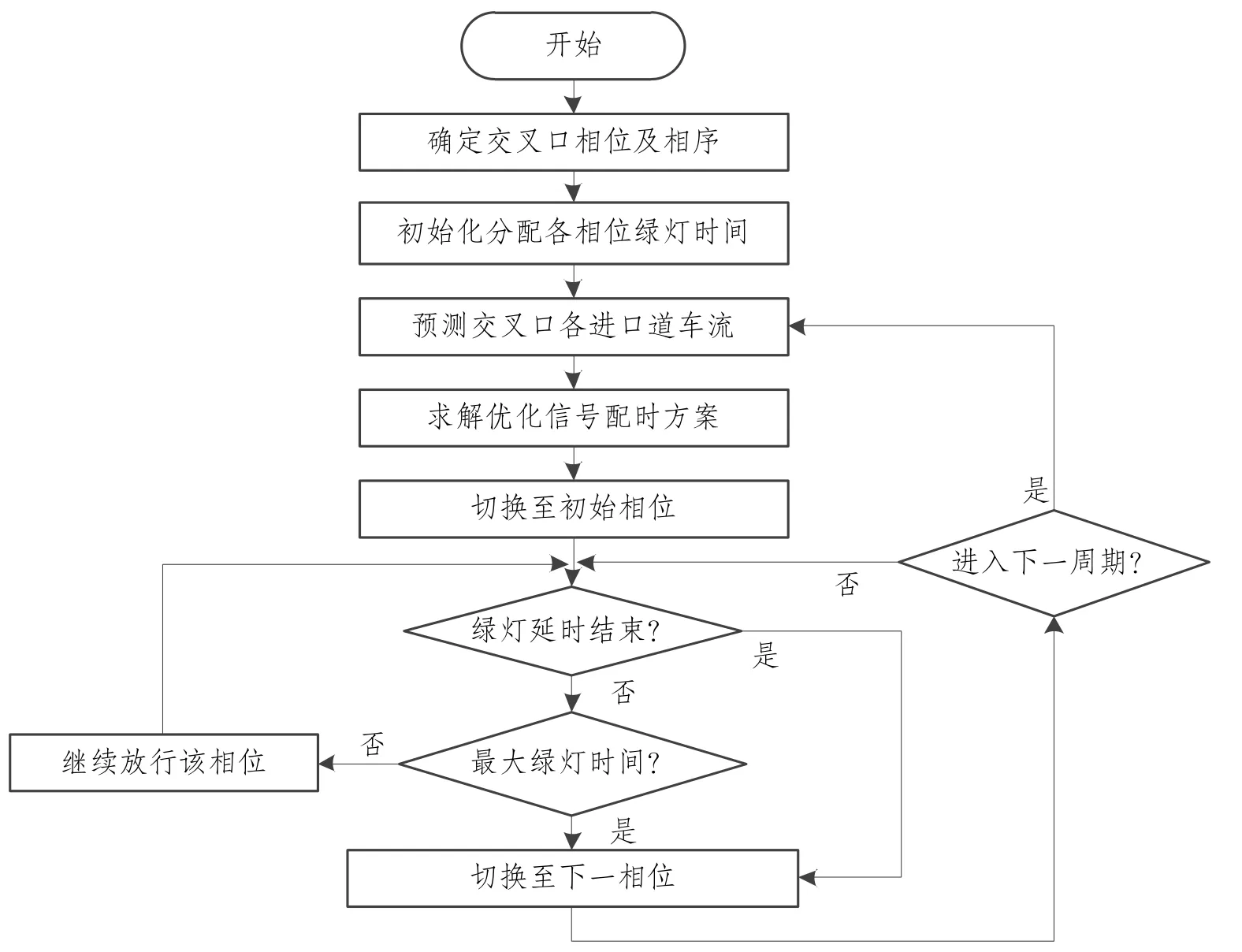
图2 车联网环境下自适应优化控制流程图Fig.2 Flow chart of adaptive control in connected vehicle environment

4 仿真实验及分析

4.1 实验路口

本文选取了成都市龙泉区“成龙大道—车城大道”十字型交叉口作为算例，通过现场调查，发现信号控制采用传统的4相位放行方式，并且采用定时信号控制方案。其中车城大道为南北走向4车道；成龙大道为东西走向5车道。交叉口的平面示意图如图3所示。

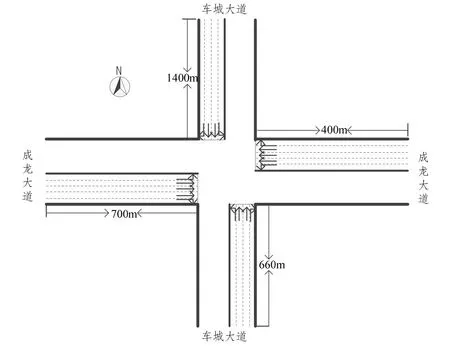
图3 成龙大道—车城大道交叉口平面图Fig.3 Intersection geometry of the Chenglong avenue-Checheng avenue intersection

为对比分析传统定时控制与本文提出的车联网环境下自适应控制的效果，实测了2017年2月23日的各进口车道早高峰（7：30～8：30）、平峰（13：30～14：30）、晚高峰（17：30～18：30）的小时交通车流量，具体数据见表2所示。表中各进口的方向与图3对应，左、直、右代表驶入各进口道后待行的方向，如北进口的左表示由车城大道北面驶入成龙大道的东面。

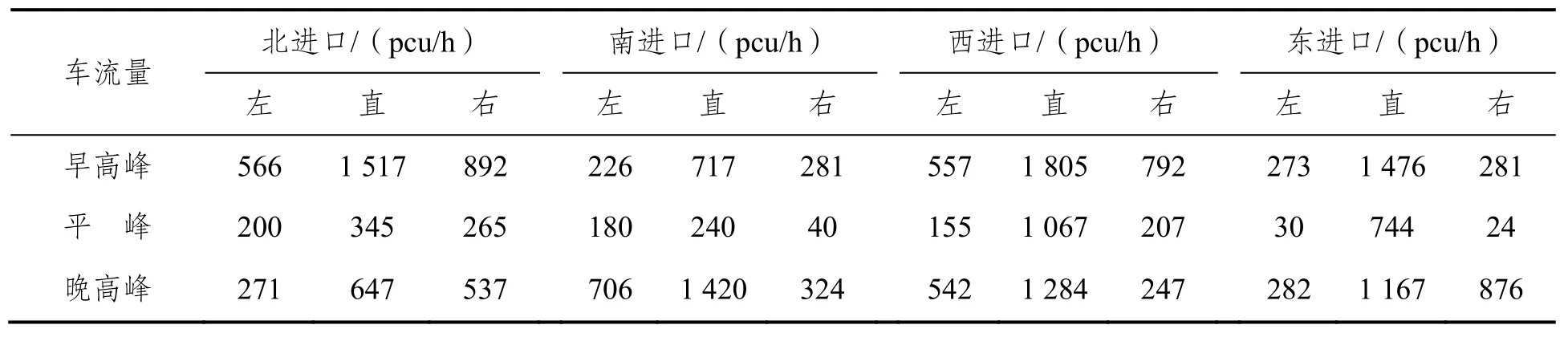
表2 高峰-平峰时段车流量数据Tab.2 Traffic demand’s during three testing periods

当然，仅与现实情况对比不足以显示本算法的有效性，本文同时采用遗传算法对优化模型求解，对比真实情况、模拟退火算法优化及遗传算法优化三种延误结果，进而说明本方法的有效性。

4.2 仿真结果

本文利用VISSIM仿真软件对建立的优化模型进行仿真实验，在MATLAB环境下对COM接口进行二次开发以实现交叉口的自适应控制。仿真中，交叉口定时信号控制的相序与时间均与实际调查的数据一致。在仿真中分别设定早高峰、平峰以及晚高峰三个时段下的小时交通量，仿真总时长为3h，分别对调查的定时信号控制与两种算法下的自适应信号控制进行仿真，统计了仿真时段内车辆的平均延误以及平均停车次数，仿真的结果对比如图4、5所示。

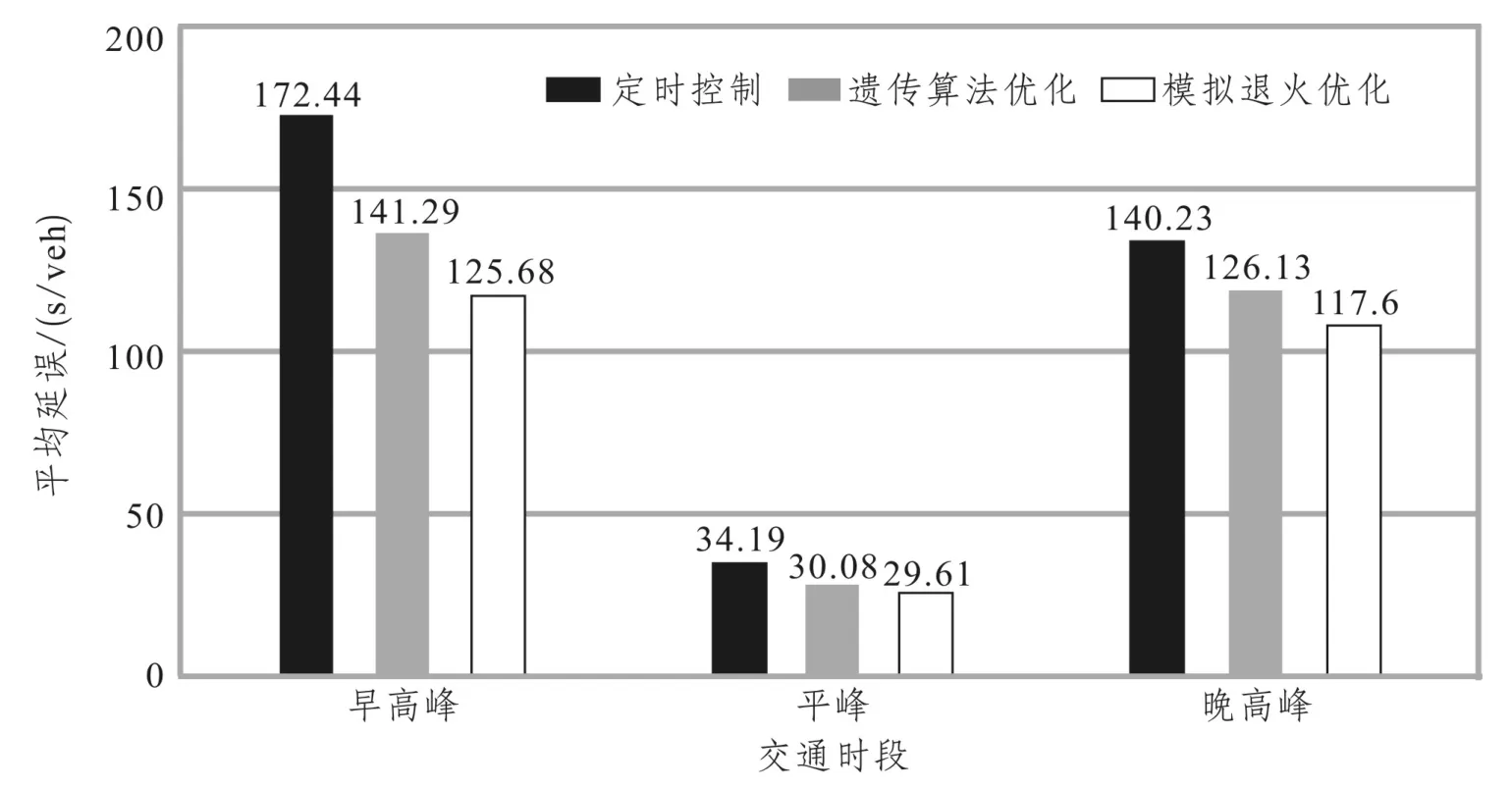
图4 交叉口平均延误对比Fig.4 Comparison of the average intersection delay

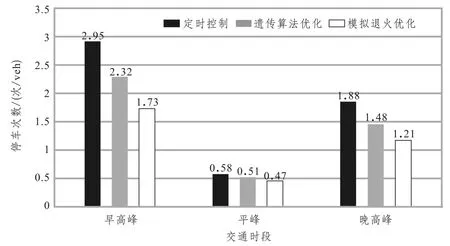
图5 交叉口平均停车次数对比Fig.5 Comparison of the average number stops

结果表明，相比于原始的固定信号配时方案，经过遗传算法和模拟退火算法优化的自适应信号控制方法能够有效提高交叉口的通行能力，且流量越大（早高峰＞晚高峰＞平峰），优化效果越明显。对比遗传算法和模拟退火算法发现，遗传算法优化效果略差，说明本文提出的模拟退火算法能够跳出局部最优解，具备有效性。与遗传算法相比，模拟退火算法在早高峰、平峰和晚高峰期间对车辆通过交叉口的平均延误节省值分别为15.61s/veh、0.47s/veh、8.53s/veh，相当于一辆车通过交叉口的延误减少了11.05%、1.56%、6.76%，单辆车的平均停车次数也分别降低了0.59次/veh、0.04次/veh、0.27次/veh。

5 结 论

车联网环境下能够实时获得交叉口的车流状态，本文以单点信号交叉口为对象，在预测各进口短期时间窗交通流到达的基础上，建立了一种基于模拟退火优化算法的交通信号控制方法与模型，从而实现了车流单向适应信号向信号主动适应车流模式的转换，最大化利用道路资源。仿真结果表明，相比于定时信号控制，自适应信号控制的效果要明显更优，同时文章提出的模拟退化算法优化程度高于一般算法。模型满足了实时性、准确性的要求，BP神经网络模型能够基于先验信息快速预测周期交通流到达规律，模拟退火算法能够准确寻找全局最优解。相比于现有模型而言能够大大减少算法复杂度，易于实现与应用，大大缩短了交叉口单车的延误时间和平均停车次数，提高了交叉口的服务水平。

当然，本文研究还缺乏对于最小、最大绿灯时间的优化，也未研究车辆之间的相互影响，后续的研究工作将从这两方面继续展开。

[1] 魏武，张起森，王明俊，等. 一种基于模糊逻辑的城市交叉口交通信号控制方法[J]. 交通运输工程学报，2001，1（2）：99-102.

[2] 吴兵 李晔. 交通管理与控制[M]. 北京：人民交通出版社，2009.

[3] HLER E，STREHLER M. Traffic signal optimization using cyclically expanded networks[J]. Networks，2015，65（3）：244-261.

[4] 刘红红，杨兆升. 基于神经网络的实时交通信号控制与仿真研究[J]. 交通运输系统工程与信息，2008，8（2）：43-47.

[5] 楼小明. 考虑交叉口影响的城市路网信号优化设计问题研究[J]. 交通运输工程与信息学报，2013，11（1）：108-113.

[6] 李瑞敏，陆化普，史其信. 基于遗传算法的交通信号多层模糊控制模型研究[J]. 武汉理工大学学报：交通科学与工程版，2009，33（3）：407-410.

[7] 田丰，边婷婷. 基于自适应遗传算法的交通信号配时优化[J]. 计算机仿真，2010，27（6）：305-308.

[8] 黄艳国，罗强，许伦辉. 基于多智能体的城市交通区域协调控制方法[J]. 武汉理工大学学报：交通科学与工程版，2010，34（2）：409-412.

[9] 张存保，陈超，严新平. 基于车路协同的单点信号控制优化方法和模型[J]. 武汉理工大学学报，2012，34（10）：74-79.

[10] 张存保，冉斌，梅朝辉，等. 车路协同下道路交叉口信号控制优化方法[J]. 交通运输系统工程与信息，2013，13（3）：40-45.