基于变精度粗糙集的缸体加工特征工艺规则提取及更新方法
2018-03-30陈贻平徐立云楼科文
陈贻平 徐立云 楼科文
缸体是多面多孔的箱体类零件,工艺复杂多样,一直是发动机生产中的难点,其加工精度和一致性直接影响汽车性能。以往企业在进行缸体加工工艺设计时,主要依靠工艺人员的经验和智慧[1]。工艺人员的经验信息隐藏在每次决策实例中,人们希望这种决策经验信息以更容易被理解的形式表示出来。因此,从已有的成功案例和经验中提取工艺规则,有利于提高工艺决策效率和质量。
粗糙集理论[2-3]是进行数据挖掘和知识发现的有效手段之一,它直接从给定集合的描述出发,通过不可分辨关系和等价类确定给定问题的近似域,从而找出该问题的内在规律。在规则提取方面,文献[4]提出了一种基于粗糙集理论的决策规则提取方法,通过分析故障实例,获取了故障诊断规则。文献[5]应用扩展粗糙集对工艺信息表进行数据挖掘提取工艺偏好知识。文献[6]在构建工艺数据集市的基础上,建立了基于粗糙集属性约简的行业工艺知识发现方法。文献[7]在产品设计本体模型的基础上,利用粗糙集和信息技术从知识使用日志中抽取了知识推送规则。文献[8]采用粗糙集理论规则学习算法,用于优化变量约束范围的规则提取,对切削参数进行优化。但传统粗糙集基于确定的等价关系进行规则提取,容易忽略工艺数据中潜在的规则。其次,在实际生产过程中,缸体加工工艺不是一成不变的[9],而上述研究者都把训练样本作为一种静态数据来处理,当数据不断扩大时,其准确性和适应性会大大下降。
本文将缸体加工工艺数据进行粗糙化处理,将处理后的数据建立加工工艺决策表,采用变精度粗糙集数据挖掘方法,从决策表中提取隐含、潜在的加工工艺规则。同时,提出缸体案例规则库的更新方法,从而使缸体加工工艺决策更准确和快速,满足产品工艺设计要求。
1 变精度粗糙集基本概念
1.1 粗糙集理论
缸体加工工艺规则的提取本质上是一个模式分类与识别问题[10],通过粗糙集理论的等价关系可以对对象集进行分类。工艺信息系统是工艺实例库的抽象描述,它是工艺对象集与工艺属性集之间的纽带,也是工艺规则提取的信息基础。工艺决策信息系统则是将工艺信息系统中的工艺属性分为工艺条件属性和工艺决策属性两类,通过两类属性之间的关系获取工艺规则。
设四元组S=(U,A,f,V)是工艺信息决策系统。其中,U为工艺实例样本集,称为论域,U={X1,X2,…,Xn},是各种特征的加工工艺实例,对于缸体而言,主要是孔、面和一些辅助特征的加工;A表示加工工艺属性集,A={a1,a2,…,am},A=C∪D,C∩D≠ø,C={a1,a2,…,am-1},表示工艺决策条件属性集,其元素多样,例如孔径、深度、粗糙度、表面质量、平面度和加工精度等;D={am},表示加工工艺决策属性集,即特征的加工方法,例如孔加工的钻、扩、铰和平面加工的铣、磨等;V表示A的值域;f为映射函数:f:U×A→V,表示对每个工艺实例对象的各属性赋予一个信息值。
定义1 设A为加工工艺属性集,A在加工工艺实例集上确定了一个不可分辨关系,记作IND(A),表示为:

按照条件属性C和决策属性D对缸体加工工艺实例样本集的划分,称为条件类和决策类,分别记为:

分别称为由C与D决定的不可区分关系。对于B∀⊂C,给出对象空间的等价关系:

从而得到样本空间U上的集合划分U/RB:

式中,B(x)=(fb(x);b∈B)是属性,[x]B是具有属性B(x)的等价类。对于任意缸体加工工艺实例样本X⊂U,存在它关于RB的上近似和下近似:

分类精度:γ(X)=|B(X)|/|U|。γ(X)反映了可能正确的知识在现有知识中的百分比。
1.2 变精度粗糙集
Ziarko[11]在标准粗糙集模型的基础上引进正确分类率β(0.5<β≤1)概念,提出变精度粗糙集模型,即允许一定程度的错误分类的存在,并通过设置阈值参数,放松标准粗糙集理论对近似边界的严格定义。对于不一致性较弱的数据,有利于从边界数据中发现潜在规则[12-13]。
定义2 对于某一X⊂U和U上的一个不可区分关系B⊆A,给定阀值β(0.5<β≤1),则称:
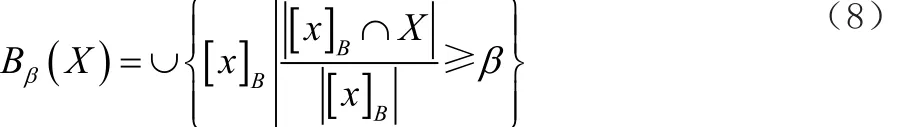
为X的B的下β近似;

为X的B的上β近似。则:
β正域:

β负域:

β边界域:
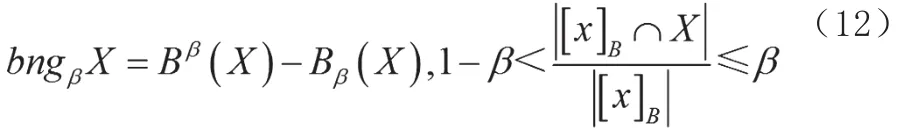
图1所示为变精度粗糙集的概念示意图,随着β减小,变精度粗糙集的近似边界区域变窄,即变精度粗糙集的不确定区域变小。由于分类精度与正确分类率呈负相关,β的取值应根据实际情况而定。

图1 变精度粗糙集概念示意图
2 基于粗糙集的缸体加工工艺属性约简及规则提取
2.1 工艺属性的预处理
影响缸体加工工艺决策的工艺条件属性很多,如:尺寸大小、加工精度、粗糙度和材料等。其中,尺寸大小,如孔径、深度等为连续型属性;加工精度,如IT9、IT10为离散型属性;材料,如HT200、HT250为字符型属性。首先要将工艺属性数据进行离散化处理,列出挖掘对象的条件属性C和决策属性D,得到样本集(论域)的属性值列表。工艺知识表达方式应具有可解释性,对工艺知识的处理不能脱离工艺语言本身的固有特征,而且还要考虑灵活的数学描述处理方式。缸体加工特征的工艺属性预处理如下。
连续型属性:孔径、孔深、深径比等属性为连续型属性,根据属性值的分布情况,对均匀分布的属性采用等宽分箱的离散化方法,取尽可能少的断点将属性空间划分为尽量少的子空间,而对非均匀分布的属性,则采用根据分布情况的自定义法进行离散[14]。
离散型属性:粗糙度和加工精度是离散型属性,可根据相应的国标或行业标准,通过模糊化处理成数值形式。
字符型属性:主要是加工材料、加工资源和加工方法等,也可通过模糊化处理成数值形式。
布尔型属性:主要是有无倒角,是否为螺纹孔等,可直接进行模糊处理,转化成数值形式。
2.2 工艺属性约简和规则提取算法
属性约简是粗糙集的理论的核心内容之一[15],缸体加工工艺属性的约简,是为了删去冗余属性,从众多纷繁复杂的工艺规则中提取核心规则。变精度粗糙集求解属性约简只能采用启发式的约简算法,而不同启发式约简算法在于对属性重要性的定义[13]。属性信息量表明该属性包含的信息的多少,信息量越大,则其分类能力越强;属性重要度反映决策属性分类对该属性的依赖程度,重要度越大,则该属性越关键。本文将属性信息量和属性重要度进行加权得到的属性依赖度,进而对属性的重要性进行定义。
定义3 条件属性信息量:

其中,|U|为论域中缸体加工案例的数量;|Xi|为根据某类等价关系划分的某个等价类所包含的案例个数。定义4 条件属性重要度:

其中,|Di|为决策类的某个等价类;|posC(Di)|为某决策类的等价类正域所包含的案例数。
定义5 条件属性C关于D的依赖度:

其中,ω为权重系数,当ω=1时,表示只考虑属性信息量;当ω=0时,表示只考虑属性重要度。
定义6 令A为加工工艺属性集,a∈A,若IND(A)=IND(A-{a}),则称a为A中不必要的;否则a为A中必要的。如果a∈A都为A中必要的,则称A是独立的;否则成A是依赖的。
定义7 设Q⊆P,如果Q是独立的,且IND(Q)=IND(P),则称Q为P的一个约简,记作red(P)。显然,P有多个约简。P中所有的必要属性组成的集合称为P的核,记作core(P)。核与约简有如下关系:core(P)=∩red(P)。
定义 8 记DP(C,D,β)={CβD1,CβD2,…,CβD|U/D|},DP 为所有决策类β下近似构成的集合,是各决策类关于U/C的概率分布,称DP为决策类下近似分布。
本文采用基于核属性的启发式约简算法,首先对缸体加工所有的条件属性集C的依赖度大小排序,依赖度最高的条件属性必然存在于核中;再依次将其它条件属性加入到依赖度最高的条件属性中,直到整个集合关于决策属性集D的下近似分布等于DP(C,D,β)。算法流程如下:
输入:缸体加工工艺信息决策系统S=(U,A=C∪D,f,V),U为论域,C为工艺条件属性集,D为决策属性集。正确分类率β,权重系数ω,C关于D的依赖度sig(C,D,β),C关于D的下近似分布为DP(C,D,β)。
输出:条件属性约简red(C,D,β)
Step1 计算属性依赖度,以依赖度对属性进行排序,假设顺序为:
sig(C1,D,β)>sig(C2,D,β)>…>sig(Cm-1,D,β)
Step2 设置初始约简集:
red(C,D,β)=C1
Step3 根据属于的依赖度大小,依次加入到初始约简集中,直到整个集合关于决策属性集D的下近似分布等于DP(C,D,β):

缸体工艺决策表经属性约简后,留下精简的工艺规则。采用支持度和准确度对工艺规则进行评价:
规则支持度:

规则准确度:

其中,S为规则前件,T为规则后件,X表示条件属性满足S的样本,Y表示决策属性满足T的样本,U为样本全集。支持度表示缸体加工工艺样本集中满足该规则的样本比例,如果支持度太小,规则就不具有代表性,设置最小支持度阀值σ,只保留大于阀值的工艺规则,可以减少规则的数目,提高提取规则的质量。准确度可作为规则发生矛盾时的评判依据。
3 缸体加工工艺规则更新方法
目前,对规则更新的研究主要集中在规则集的更新方面,一般只考虑新增案例与原始规则的冲突包含和重复关系,忽略了新增案例与原始数据库的属性约简表的关系。同时,传统规则更新方法在处理新案例时,只考虑单次新案例的影响,但工艺数据库是动态积累的,传统方式不能体现这个积累过程。因此,本文在进行新旧规则更新时,对满足最小支持度的“淘汰规则”做保留处理,而不是简单剔除,随着案例库的不断更新,“淘汰规则”可能被重新利用。
定义9 对于缸体加工工艺决策表S=(U,A=C∪D,f,V),B为C的一个约简B⊆C,新案例X加入数据库后,对于y∀⊂U,可以区分新案例X。
本文从属性约简表和规则集两方面进行考虑,工艺规则集的更新产生的影响分为四种情况,图2为新增案例决策流程,四种情况的处理方案如下所述。

图2 新增案例决策流程
情况A:新增规则与原始规则未产生矛盾,同时原始规则可以覆盖新增规则,规则集R不变。
情况B:新增规则与原始规则未产生矛盾,原始规则集不能覆盖新增规则,将新规则直接添加到规则集,更新规则集为R´。
情况C:新增规则与原始规则有矛盾,例如:原始规则A和新增规则B的规则前件完全相同,但是规则后件不同,计算新规则的支持度,若不满足最小支持度,σ,原始规则集不变,新规则直接淘汰;若满足最小支持度,再计算比较新旧规则的准确度,取准确度大的规则,更新规则集,准确度小的规则作为备用规则储存在备用规则集RS。实例库不断增大,当某备用规则支持度小于σ时,剔除该备用规则。若备用规则支持度大于规则集中与之矛盾的规则,替换原该规则更新规则集为R´。
情况D:原始约简集不能区分新案例,更新案例库,重新计算属性约简,并提取规则。
4 实例应用
为方便说明问题,本文仅以缸体一阶孔为例来进行规则提取和更新,表1列出多种型号缸体中统计出的20个孔的工艺特征信息。

表1 缸体加工案例
缸体加工工艺案例库中的工艺信息数据根据本文提出的预处理方法进行处理。对于工艺案例中缺失的数据按照最低加工要求进行处理,比如“3”号孔的加工精度和粗糙度要求缺失,说明其加工精度和表面质量要求不高,就按照IT8以下和Ra 12.5处理。表2为工艺数据处理的对照表。

表2 工艺属性—数学表达对照表
获得加工工艺决策表,如表3所示。U为论域表示孔的集合,C1表示孔径,C2表示深度,C3表示深径比,C4表示加工精度,C5表示粗糙度,C6表示材料,C7表示是否为螺纹孔,D表示加工路线。例如,X2(21123212)表示论域中的第二个孔,其孔径在10~20mm,深度小于30mm,深径比在0~1,加工精度为IT8,粗糙度为Ra3.2,材料为HT200,非螺纹孔,其加工路线为钻—扩—铰。

表3 加工工艺决策表
4.1 工艺属性约简和工艺规则的提取
决策属性D对缸体加工工艺实例样本集的划分为:


条,,件属性C对缸体加工工艺实例样本集的划分为:
为了达到一定的分类精度,根据分类精度和正确分类率的关系,结合实际情况,本文取β=0.7,则各决策类β下近似分布DP=(C,D,β)为:

按照式(3)对各条件属性依赖度进行计算,取ω=0.5,依赖度计算结果如表4所示。

表4 依赖度计算结果
由计算结果可知,Sig(C4)>Sig(C5)>Sig(C1)>Sig(C3)>Sig(C2)>Sig(C6)。因此,核属性取C4。根据条件属性依赖度的大小依次将各条件属性添加至核属性,分别计算条件类。首先将C3添加至核属性,即red(C,D,β)=C4∪C3,DP(red(C,D,β),D,β) ≠ DP(C,D,β),C4∪ C3不 是属性的约简。重复以上操作,直到添加到C3时,DP(red(C,D,β),D,β)=DP(C,D,β)。最后属性约简为 {C1,C3,C4,C5},属性约简结果如表5所示。

表5 属性约简结果
经属性约简后的决策表可以看作是一个规则集合,每条决策规则都精准地对应该决策表中的一个实例。计算每条规则的支持度和准确度,取σ=0.03保留支持度不小于最低支持度阀值的规则;对于有矛盾的规则,保留准确度较大的,同时将准确度较小,但支持度不小于支持度阀值σ的规则作为备用规则保存;若准确度相同,将这些规则都作为备用规则保存。由此获得以下11条工艺规则,得到工艺规则集R,同时有2条准确度相同,支持度达到阀值,但是有矛盾的规则,构成备用规则集RS。

表6 规则集
4.2 规则更新
采用该企业某新缸体的10个一阶孔作为加工案例对原有规则集进行更新,表7为新增孔案例,表8为新增孔的工艺决策表。

表7 新增孔案例
条件属性子集B={C1,C3,C4,C5},根据定义9的描述,对于,即约f(x,a)≠f(y,a),f(D,a)≠f(y,D)即约简属性可以区分新案例,获得的新案例规则集RN如表9所示。
规则o)、q)、r)属于情况A,新增规则未与原始规则冲突,且原始规则集包含新规则,规则集R不变,修改支持度和准确度;规则n)属于情况B,新增规则未与原始规则冲突,且原始规则集不包含新规则,将n)直接添加到规则集;规则p)属于情况C,新增规则未与原始规则冲突,但是符合备用规则集中规则m),使其准确度和支持度分别增大至0.67和0.10,将规则m)添加到规则集。更新后的加工工艺规则集如表10所示。更新后,规则更加细化,新增的规则可以覆盖更多的工艺案例,提高了规则集的精度。

表8 新增工艺决策表

表9 新增加规则集

表10 新规则集
4.2 结果验证与分析
Machining Line Planner(MLP)是Siemens公司开发的发动机缸体、缸盖工艺规划软件,可以通过接口对其规则库进行提取和更新,满足企业的实际生产需求。
首先将更新后的规则分别添加到MLP规则库中,如图3所示。利用提取的工艺规则,计算不同属性孔特征的加工路线,得到的实验结果如表11所示。例如,34号孔的孔径为10mm,深径比为1.1,加工精度为U8,粗糙度为Ra1.6,其工艺属性对应工艺规则“a)IF(C1,1)∧(C3,1)∧(C4,2)∧(C5,4)∧THEN D=2”,输出加工路线为钻-扩-铰,与实际加工情况一致。

图3 规则库

表11 实例验证结果
5 结语
采用变精度粗糙集理论对缸体加工工艺规则进行提取和更新,克服了传统工艺设计单纯依靠经验知识的局限性。通过将现有7个工艺属性的缸体加工工艺信息进行分析和简化,提取了隐藏在工艺信息里的加工规则,以直观的方式描述出来,提高了工艺规则提取的效率和规则的准确性,为箱体类零件的加工工艺设计提供借鉴。
[1]秦宝荣.智能CAPP系统的关键技术研究[D].南京:南京航空航天大学,2003.
[2]Fan Y,Bill Tseng T,Chern C,et al. Rule Induction Based on an Incremental Rough Set[J].Expert Systems with Applications,2009,36(9):11439-11450.
[3]Pawlak Z,Skowron A. Rudiments of Rough Sets[J].Information Sciences,2007,177(1):3-27.
[4]黄文涛,赵学增,王伟杰,等.基于粗糙集理论的故障诊断决策规则提取方法[J].中国电机工程学报,2003,(11):154-158.
[5]王忠浩,邵新宇,张国军,等.基于扩展粗糙集的工艺偏好知识发现[J].机械工程学报,2005,(7):84-89.
[6]薄洪光,刘晓冰,马跃,等.基于粗糙集的钢铁行业工艺知识发现方法[J].计算机集成制造系统,2009,(1):135-141.
[7]吉祥,顾新建,代风,等.基于本体和粗糙集的产品设计知识推送技术[J].计算机集成制造系统,2013,(1):7-20.
[8]蒋亚军,娄臻亮,李明辉.基于模糊粗糙集理论的模具数控切削参数优化[J].上海交通大学学报,2005,(7):1115-1118.
[9]Guo S,Wang Z Y, Wu Z C, et al. A Novel Dynamic Incremental Rules Extraction Algorithm Based on Rough Set Theory[C]. International Conference on Machine Learning and Cybernetics. 2005,(3):1902-1907.
[10]王金涛,谢友柏.油液故障诊断系统知识发现的包含度方法[J].机械工程学报,2003,(9):58-61.
[11]Ziarko W. Variable Precision Rough Set Model[J].Journal of Computer & System Sciences,1993,46(1):39-59.
[12]黎文航.基于变精度粗糙集理论的焊接动态过程知识建模方法研究[D].上海:上海交通大学,2007.
[13]陈昊,杨俊安,庄镇泉.变精度粗糙集的属性核和最小属性约简算法[J].计算机学报,2012,(5):1011-1017.
[14]李远远,云俊.基于粗糙集的指标体系优化及评价方法研究[J].浙江大学学报(理学版),2010,(4):411-415.
[15]米据生,吴伟志,张文修.基于变精度粗糙集理论的知识约简方法[J].系统工程理论与实践,2004,(1):76-82.
