CFD技术在动车组空调送风道设计中的应用
2018-03-30蒲栋
蒲 栋
1 研究背景
随着高速铁路技术的发展,人们轨道车辆的乘坐舒适度要求越来越高,空调通风系统作为提高乘坐舒适度的必要硬件设备,合理的通风方案能够有效改善、提高列车的乘坐舒适。研究高速动车组空调通风系统内空气的流动均匀性,提出相应改进措施,对指导动车组空调通风系统设计有理论价值和现实意义。
张吉光[1-7]、谈越明[8]等人对静压送风风道的送风性能等进行了试验研究,分别提出了在静压腔的主送风道应为变截面风道及在主风道内增加阻力板的送风均匀性调整方法,邓建强[9]等人模拟复杂结构风道内三位流场及其送风口送风特性等,研究了主风道内隔板及导流板高度等对风道送风均匀性的影响。
目前,国内动车组典型的送风型式包括与铁路客车相似的静压送风、散流式孔板送风型式等。上述学者对铁路客车静压送风的风道送风均匀性进行了试验和数值模拟研究,对于散流式孔板送风的研究未见相关报告。本文对散流式孔板送风道内空气流动特性进行研究,通过CFD(Computational Fluid Dynamics)技术预测其流动特性,确定风道各风口的风量分配等相关参数,为散流式孔板送风的设计及试验提供理论依据。本文以某型动车组风道设计为实例,结合CFD仿真技术在轨道车辆风道系统中的应用,提出一种基于仿真与风道配套试验结合的动车组风道系统设计方法。
2 基于CFD的风道流场计算
所有可通过CFD技术进行计算的问题,其求解流程如图1所示,包括建立控制方程、创建几何模型、确定计算条件(边界及初始条件)、模型的网格划分、建立偏微分方程、确定偏微分方程的计算条件(边界及初始条件)、给定求解控制参数、求解偏微分方程、显示计算结果。
2.1 流场分析求解控制方程
风道内的流体为具有稳定、粘性较小及紊流等特性,通过采用带有浮力特性的高雷诺数k-ε两方程紊流模型对流场进行三维紊流计算[10],进行以下假设:
(1)风道内气流为不可压缩流体,满足理想气体状态方程;

图1 基于CFD的流场计算流程
(2)流体表面应力符合牛顿粘性应力公式;
(3)风道内气体的紊流粘度各向同性;
(4)流体密度的变化仅对浮力产生影响,仅在计算浮力时考虑密度的变换;
(5)采用 ρ=ρ0(1-β·∆T)(式中 ρ0为流体的常密度,β为膨胀系数)消除浮力项中的ρ。
风道内空气流场分析需用到的控制微分方程包括连续性方程、动量方程及能量方程,由上述方程共同组成一个控制方程组,用于求解风道内气体流场的各个参数[11]。

式中:ux、uy、uz为速度分量,p为静压力,Fx、Fy、Fz为微元体受到的体积力,ρ为流体的密度,k为流体的传热系数,cp为比热容,ST为粘性耗散项,β为膨胀系数,ρ0为流体的常密度,T表示温度,T0为工作温度。
偏微分方程组采用有限体积法求解,方程对流项采用二阶精度的迎风差分格式,压力速度的耦合采用SIMPLE算法。
2.2 几何模型处理
2.2.1 创建几何模型
利用建模软件建立模型,考虑到仿真计算的复杂程度和计算时间,其中一些细节部分如风管内加强筋,管道连接处法兰等因素未加载到模型内,风道几何模型如图2所示。同时,根据风道安装形式,将各块进行编号处理,便于数据分析及优化,如图3所示。
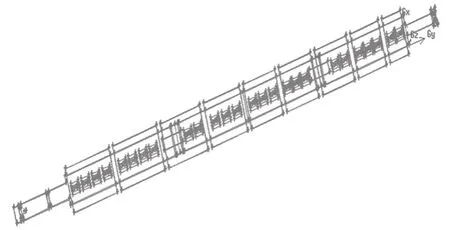
图2 送风道几何模型

图3 模型编号
仿真模型所涉及的送风参数如表1所示。

表1 送回风参数
2.2.2 网格划分及边界条件设置
采用数值方法求解控制方程时,需将控制方程在控件区域上进行离散,然后求解得到离散方程组,这就需要对三维模型进行网格划分处理。在网格处理时选择合适的网格尺寸,在边界和几何复杂区域进行加密处理,可提高仿真计算的精度。本文利用gambit对模型划分网格,网格形式为TGrid,如图4所示。

图4 风道网格划分
风道边界条件类型分为Velocity inlet和Pressure outlet,包括入口风量、出口压力及k和ε,具体参数详见表2。

表2 送风道仿真分析边界条件设置参数
2.3 计算结果及分析
可通过调整图5中散流器的高度h对风道的送风均匀性进行优化。

图5 送风孔板优化措施
对风道进行基于CFD技术的流场仿真,并对仿真数据进行分析,结合风量的不平衡率及风道的优化措施,对风道方案进行优化,并验证优化措施的有效性。
风道方案的仿真计算结果见表3,其风速分布见图6。由表3可以看出,除编号1、4、7、9、T1外,其余位置的风速不平衡率均超过了15%,绝对值最大为62.90%,不满足送风均匀性的设计要求。从图6可以看出风道内最大风速为9.93m/s,不满足送风道风速设计标准5~8m/s的要求。
按照图5所示的方案对风道进行优化,仿真计算数据见表4,从表4中的数据可以看出风速的最大不平衡率绝对值为9.72%,小于10%,满足送风均匀性的要求,进而保证车内的送风均匀性及温度均匀性。
图7为优化后送风道内的风速分布图,可以看出,风道经过优化后,风道内的最大风速为6.8m/s,满足送风道风速设计标准5~8m/s的要求,由此说明基于图5所示的通过缩小或增大孔板面积的方法对送风道进行优化的方法可行。合理控制风道内的风速,可有效降低空调系统的送风噪声,提高客室的乘坐舒适性。
2.4 风道配套试验数据校验
结合风道配套试验,对表4中的试验数据进行校验。首先进行风道模型的制作,采用铝板材质,通过风道配套试验台(见图8)模拟送风,试验数据见表5。
通过对表5的数据进行分析,可得送风量的总和为7053m3/h,大于设计值7000m3/h,与设计值的偏差为0.76%,而且各个孔板上的风量偏差都控制在10%以内。对风道内风速进行测试,风速最大为7.45m/s,满足送风道内风速5~8m/s的要求。

图6 送风道风速分布图

图7 优化后风道风速分布图

表4 优化后送风道仿真计算结果

图8 风道配套试验台
因此,通过仿真计算后对散流器高度进行调整的方法,在风道的送风均匀性设计中应用是合理的。

表5 风道配套试验中测试数据
3 结论
综上所述,CFD仿真在理论上有效地指导了风道的理论设计,将CFD与工程研究相结合是一种有效和经济的研究手段。由于在仿真中对模型进行了一定简化,且对风道的后期改进未及时体现在仿真模型当中,可能使模拟结果产生一定偏差,总结如下。
第一,在进行仿真时风道的某些参数尚未确定,如管道的摩擦系数等,同时也对风道的某些细节部位进行了适当简化,这些问题会对计算结果产生一定影响。
第二,仿真设置中,空气在进入风道时都是与法线方向平行的,进口处都是均匀流,但在实际情况下由于管路的复杂性,流体的流态往往在进口处发生较大波动。送风是通过人字型板的分流后进入送风道的,设置两个送风口,其中,送风道的中间送分部分是由两个送风口同时相对送风的,气流组织比较复杂。
以上问题,涉及的模型参数可以根据试验数据进行确定,同时将在后续工作中对各部分的局部流动状态进行分析,尽量减少模型简化带来的影响,并考虑对整车风道进行模拟分析,以消除由于各部分单独分析带来的影响。
[1]杨晚生,张吉光,张艳梅.新型空调均匀送风道静压腔均衡衰减特性研究[J].广东工业大学学报,2005,(3):105-108.
[2]杨晚生,张吉光,张艳梅.静压式空调送风道送风均匀性研究[J].铁道运输与经济,2005,(1):79-81.
[3]张吉光,史自强,杨晚生.空调静压送风道合理结构的分析研究[J].制冷空调与电力机械,2002,(4):24-27.
[4]张吉光,史自强,杨晚生.铁路客车空调送风道试验台的研制[J].暖通空调,2002,(4):104-106.
[5]张吉光,杨晚生,史自强.静压送风道空气动力学性能的试验研究[J].流体机械,2002,(7):4-7.
[6]杨晚生,张吉光,史自强.现有客车空调送风均匀性的改进措施研究[J].铁道标准设计,2005,(4):89-92.
[7]张吉光,杨晚生,史自强.铁路客车空调送风道送风均匀性的研究[J].流体机械,2002,(11):50-53.
[8]谈越明.静压式送风风道的结构分析及试验研究[J].铁道车辆,2001,(6):11-15.
[9]邓建强,靳宜勇,张早校,等.空调客车内风道三维湍流流动特性数值研究[J].制冷学报,2001,(1):30-34.
[10]张兆顺,崔桂香.流体力学[M].北京:清华大学出版社,2006:349-350.
[11]杨永,宋文萍,张正科等译.空气动力学基础[M].北京:航空工业出版社,2014:103-184.
