秦九韶多项式在应变式称重传感器非线性校正的应用
2018-03-30黄永刚
黄永刚
(中国铁道科学研究院 标准计量研究所,北京 100015)
称重传感器被称为电子衡器的心脏部件。随着科学技术的飞速发展和微处理机的出现,工业生产过程自动化程度的不断提高,称重传感器已成为过程控制中的一种必需装置。由称重传感器制作的电子衡器也已广泛地应用到各行各业,实现了对物料快速、准确地称量。
电阻应变式称重传感器由于具有准确度高、测量范围广、寿命长、结构简单、频响特性好、能够在恶劣条件下工作、易于实现小型化整体化和品种多样化等优点,成为应用最广泛的称重传感器。
它的一个缺点就是对于大应变有较大的非线性,这是由多方面的原因造成的。对于数字应变式称重传感器而言,由于集成了弹性元件、信号调理模块和数据采集卡等部分,称重传感器各部分的非线性特性[1-3]合成了整体的非线性特性。过去,通常采用硬件电路对非线性误差进行补偿[4]。随着计算机技术的广泛应用,尤其是微型计算机和嵌入式微处理芯片的迅速发展,人们开始关注计算机处理数据的能力,使用软件进行传感器特性的非线性补偿。常用的方法有最小二乘法[5-6],支持向量机法[7]、神经网络法[8-9]等,尤以最小二乘法最为简单实用。
在此,采用软件和硬件相结合的方法校正称重传感器的非线性特性。称重传感器的输出电压经过一个以单片机为核心的非线性校正环节。该环节以多项式为数据处理模型,在计算多项式的值时,采用秦九韶算法,以减少运算次数,缩短运算时间,节约单片机的存储空间。试验结果证实该方法的正确性和有效性。
1 非线性修正的算法实现
1.1 基于最小二乘法的曲线拟合
称重传感器在正式使用前必须进行静态标定(校准),得到该传感器的输出信号与载荷的关系(输出曲线),以此作为使用过程中的计量依据。假定,标定过程中加载砝码的质量为,称重传感器的输出电压为u,称重传感器输出电压对载荷的函数关系为

在实际工作中,对载荷的测量是其逆过程,即通过测量到的电压推算出载荷质量,即

构造一个函数


图1 测量系统框图Fig.1 Measurement system block diagram
由数值分析理论[10]知,任何一个初等函数均可以用一个适当的n次多项式去充分逼近它,因此式(3)可由n阶多项式表示为

式中:a0,a1,…,an为 n 次多项式的系数;ε 为高阶无穷小。标定点的示值残差的平方和函数为

式中:i=0,1,2,…,m;m=标定点个数-1。
根据最小二乘法原理和多元函数求极值条件,要使标定点残差的平方和达到最小值,将函数s=v(a0,a1,a2,…,an)分别对 a0—an求偏导,并令各偏导数等于零即可

联立式(4),式(5)和式(6),整理得到正规方程组


式(7)可以写为

则最终得到A的表达式为

由上述分析可知,用 span{1,x,x2,…,xn}上的多项式拟合,首先需要求解一个n+1的线性方程组。一般地,n值由所要求的精度确定。有时为了提高测量精度,可能需要增大n的取值。而当n较大时,正规方程的系数矩阵会出现病态[10],可以采用其它方法求解多项式系数,从而避免正规方程组的病态。
QR(正交三角)分解法,将矩阵分解成一个正规正交矩阵Q与上三角形矩阵R,是目前求一般矩阵全部特征值的最有效并广泛应用的方法[10]。它有现成的Matlab指令可供调用,简单快捷,易于实现。利用QR分解法求解多项式系数的程序流程如图2所示。
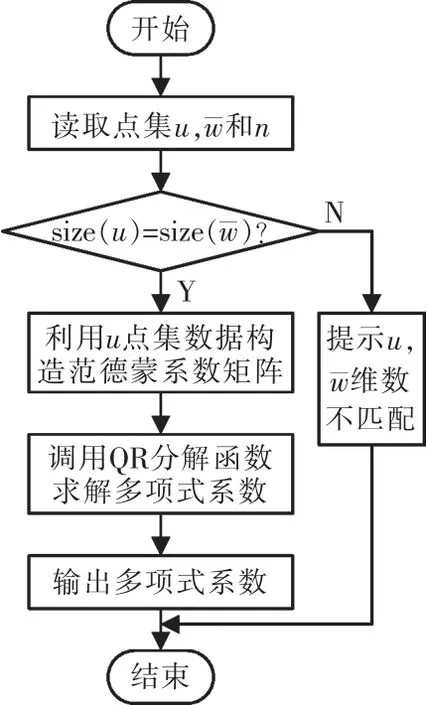
图2 利用QR分解法求解多项式系数的程序流程Fig.2 Program flow chart of solving polynomial coefficients using QR decomposition method
1.2 多项式求值的秦九韶算法
一个计算问题如果能减少运算次数,不仅可节省计算量,还可减少舍人误差。这是算法设计的重要原则之一,以多项式求值为例,设给定n次多项式
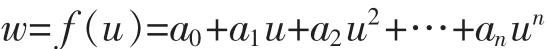
求ui处的值f(ui)。若直接计算每一项anun再相加,共需求解

次乘法,n次加法。若采用

可表示为

则bn=f(ui)即为所求。此算法称为秦九韶算法[10]。依此计算n次多项式f(u)的值,只用n次乘法和n次加法,乘法次数由 O(n2)降为 O(n),且仅使用 n+2个存储单元。这是计算多项式值最好的算法。该算法是我国南宋数学家秦九韶于1247年提出的,国外称其为Hernor算法,在1819年给出,比秦九韶算法晚了500多年。
2 试验标定及多项式系数求解
对量程为15000kg的称重传感器进行加载测试,其加载砝码质量和称重传感器的输出电压见表1。

表1 标定实验数据Tab.1 Calibration experiment data
从理论上分析,称重传感器载荷和输出电压之间的函数关系可进行任意次多项式拟合。根据精度的要求,取 n=5,则式(4)为
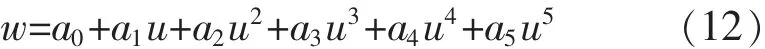
根据表1数据及前述非线性修正算法的原理,可求得多项式(12)各系数a0—a5的值为

从而求得式(12)的表达式为
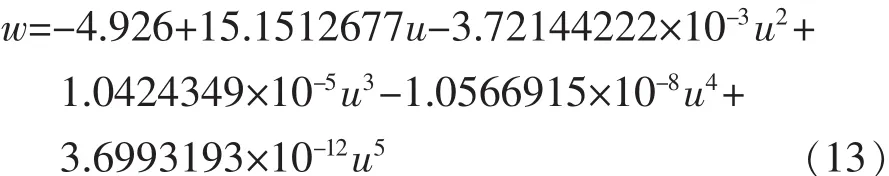
化为秦九韶算法的多项式表达式为

3 系统实现
具有非线性校正功能的应变式称重传感器的关键技术在于非线性校正环节的处理方法,基于最小二乘法进行曲线拟合,建立非线性校正拟合多项式(式(13)),化为秦九韶算法的多项式表达式(式(14))后,利用编程语言将校正过程写入单片机中。单片机与传感器数据采集部分的输出相连,收集前向环节的输出数据,并利用储存的处理方法对数据进行修正,最终输出测量系统的示值。
3.1 硬件实现
由于应用简单灵活、安全稳定、成本低和软件复杂程度低等优势,具有更少引脚和存储的8位MCU长期处于垄断地位,在未来仍会吸引市场的注意。在智能化控制领域,MCU长期处于8位机时代,竭尽全力发展与物理对象相关的控制功能[11]。在此,非线性校正环节以ATMEL89C52单片机为核心,包含非线性校正环节、以数字应变式称重传感器为基础的测试系统的硬件电路框图如图3所示。
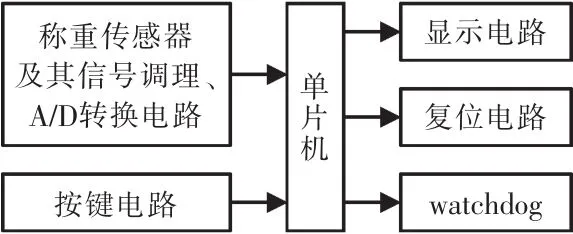
图3 测量系统硬件框图Fig.3 Measurement system hardware block diagram
3.2 软件部分
程序设计包括主程序、按键中断子程序、通信中断子程序。其流程如图4所示。

图4 主程序流程Fig.4 Main program flow chart
编写完成的软件程序,在集成开发环境下运行成功后,再送入仿真器内进行仿真调试。实现预期的功能后,用编程器将程序写入单片机内部进行独立运行。
3.3 算法比较与仿真调试
以单片机或SOC(system on chip)为核心的智能仪器仪表中,普遍采用C语言编程[12]。在Keil平台也采用C语言进行编程,数据变量采用float型运算,在进行仿真调试的过程中,将表1数据代入式(13)和式(14),分别采用常规算法和秦九韶算法求多项式的值,2种算法的运算时间对比分析和秦九韶算法运算结果及误差见表2。
由表可知,采用秦九韶算法进行多项式求值的运算时间约缩短至常规算法的1/2。2种算法的运算时间分布如图5所示。
仿真调试的编译结果还显示,常规算法的运算语句程序代码占用的存储空间为893 B,而秦九韶算法缩减至710 B。
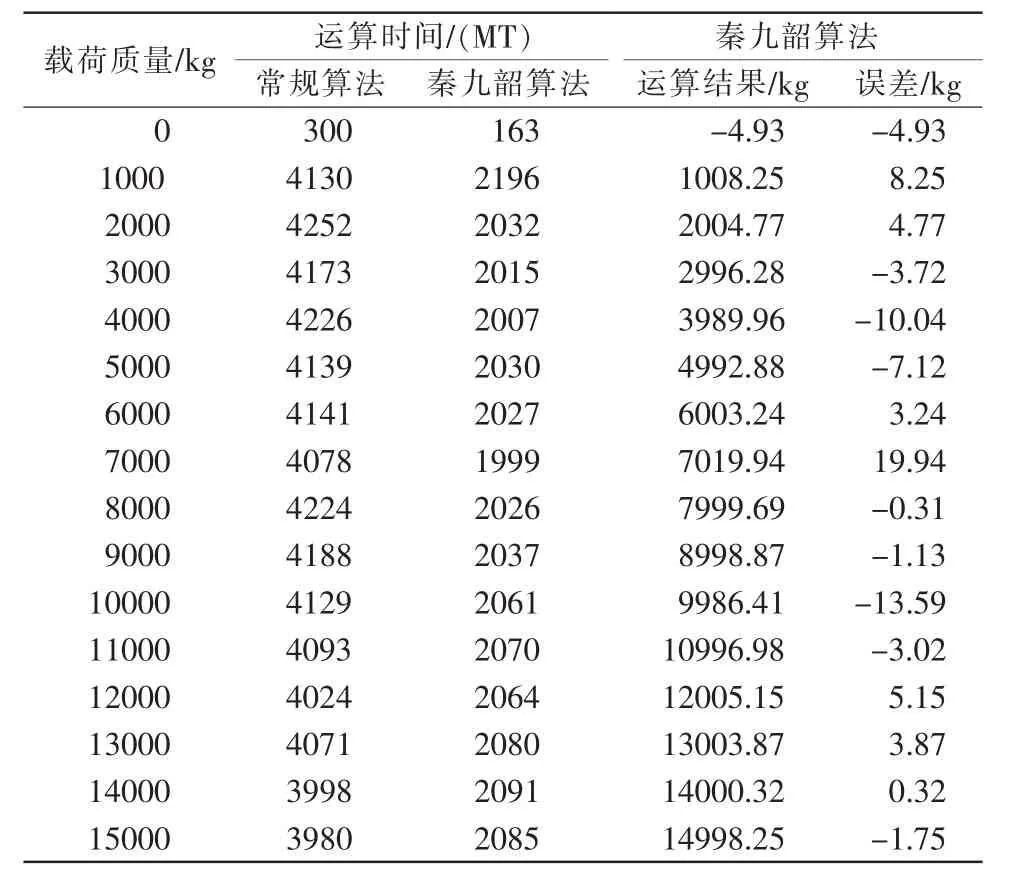
表2 仿真调试结果Tab.2 Simulation debugging results
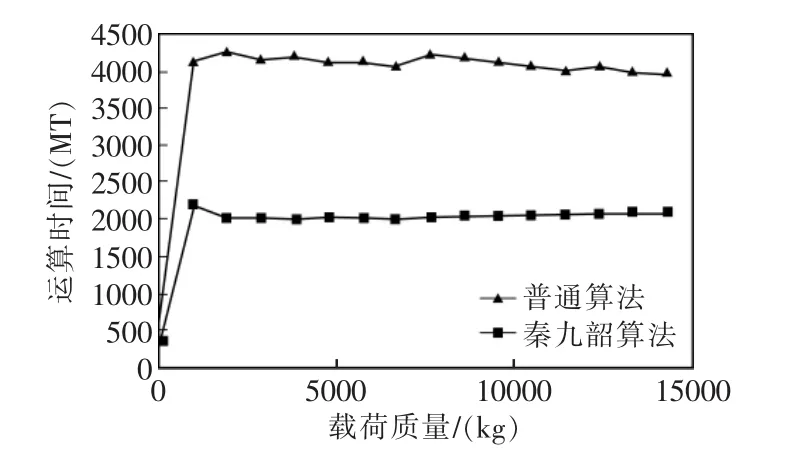
图5 算法的运算时间分布Fig.5 Operation time distribution of the algorithm
经过非线性校正处理后,测量系统的示值最大偏差为19.94 kg,满量程时相对误差为100%=0.133%,满足0.2%的测试要求。校正后误差分布情况如图6所示。
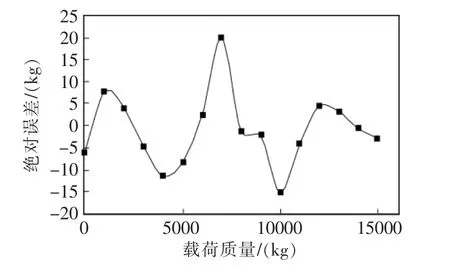
图6 误差分布Fig.6 Error distribution
4 结语
采用最小二乘法进行曲线拟合建立非线性校正拟合多项式,将校正过程存储于单片机中,对应变式称重传感器进行非线性校正。试验结果表明,经过非线性校正后,测量结果的最大绝对误差为19.94 kg,即最大引用误差为0.133%,满足0.2%的测试精度要求。如果遇到标定值的示值非线性误差不太理想等情况,可能需要调整多项式的次数或者改变拟合曲线的形式,以确保测量精度满足实际需要。
进行多项式求值运算时,秦九韶算法占用存储空间小,运算速度快,在单字节8位单片机中具有较高的应用价值。
[1]刘剑平,蔡红英,吕秀珍.称重传感器弹性元件结构参数对非线性误差的影响[J].机械工程师,2005,37(9):94-95.
[2]彭原,倪勇,左建中,等.测力传感器非线性误差研究[J].冶金设备,1995,17(4):6-9.
[3]魏俊波,张士勇.对传感器非线性误差的研究[J].大学物理实验,2005,19(1):16-18.
[4]王瑞玲.电阻应变式测力传感器线性化电路的设计与分析[J].计量与测试技术,2005,32(1):16-17.
[5]景婧.应变式称重传感器的非线性校正[J].计算机应用研究,2013,30(1):189-191.
[6]谢煜,杨三序,李晓伟.基于反拟合法的电容称重传感器非线性校正[J].仪器仪表学报,2007,28(5):923-927.
[7]WANG Xiaodong,YE Meiying.Hysteresis and nonlinearity compensation of relative humidity sensor using support vector machines[J].Sensors and Actuators B:Chemical,2008,129(1):274-284.
[8]蔡煜东,姚林声.传感器非线性校正的人工神经网络方法[J].仪器仪表学报,1994,15(3):299-302.
[9]PATRA J C,ANG E L,DAS A,et al.Auto-compensation of nonlinearinfluence ofenvironmentalparameterson the sensor characteristics using neural networks[J].ISA Trans,2005,44(2):165-176.
[10]李庆扬,王能超,易大义.数值分析[M].北京:清华大学出版社,2008.
[11]单片机与嵌入式系统应用编辑部.8位单片机是否将被32位单片机替代[J].单片机与嵌入式系统应用,2015,15(1):1-2.
[12]吴志祥,周祥才,黄亮,等.多项式直接拟合在铂电阻高精度测温中的研究[J].自动化与仪表,2014,34(2):57-60.
