基于FPGA和ARM的飞行器控制系统设计
2018-03-30范君健吴国东王志军
范君健,吴国东,王志军
(中北大学 机电工程学院,太原 030051)
随着科学技术的不断进步,无人机无论是在军事还是民用领域都有着广阔的应用前景。近年来,对无人机的研究越来越得到各国研究机构与科技公司的重视,在军事侦察、空中拍摄、交通监控及自然灾害勘察等领域,小型无人机由于其体积小巧、使用灵活的特点,将逐步取代人工成为主要的信息源。然而,无人机的核心控制系统不可避免的要涉及到飞行器的姿态、速度、位置这几个方面的控制运算,因此对于控制器的运算能力有很高的要求[1]。
现阶段常见的控制系统一般采用ARM、DSP等高速高性能处理器作为控制芯片。对于单控制器飞控系统,要在指令周期内完成无人机姿态数据采集、计算控制量并输出到执行机构、接收地面控制指令以及回传位置信息等操作[2],因此对于控制系统的可靠性提出了严峻的挑战。针对这一问题,本文设计了一种基于FPGA和STM32的飞行控制系统,使用FPGA作为数据采集与处理单元,使用STM32芯片作为控制、通讯以及人机交互单元。由于FPGA并行处理的特点,对于多个传感器的数据可以实现同步采集,能够更加精确地实现无人机的姿态与位置计算,保证了控制系统的高效稳定。同时STM32由于其低廉的成本、灵活多样的接口设置以及高效的开发流程,对于数据的存储与传输、人机交互、操作系统等的设计提供了极大的便利。
本文首先介绍了控制系统的总体方案,然后对关键部分进行详细分析与验证。通过Matlab设计算法,并对其进行仿真和FPGA的硬件实现,设计FPGA与STM32通讯接口,实现数据的高速传输。
1 四旋翼飞行器整体设计
该设计中使用的FPGA采用Altera公司Cyclone IV E系列的EP4CE10F17I7N,ARM芯片采用ST公司的STM32F407系列,STM32与FPGA通过可变静态存储控制器FSMC(flexible static memory controller)接口连接,并加入256 MB的SDRAM作为数据缓冲器。FPGA部分有陀螺仪传感器、三轴加速度传感器、地磁传感器、气压传感器,STM32部分有GPS模块、遥控器无线模块以及SD卡存储模块。系统结构如图1所示。

图1 系统结构Fig.1 System block diagram
2 硬件系统设计
2.1 系统硬件选型
模拟量传感器三个单轴陀螺仪(ENC-03MB)焊接为 X、Y、Z三个方向,三轴加速度传感器(ADXL335)。模拟量传感器可以高速而精确地进行数据采集,配合高精度多通道AD芯片AD7606,满足姿态控制的频率要求。
数字量传感器电子罗盘(HMC5983),气压传感器(MS5611)。所选数字量传感器使用相对简单,便于数据处理,同时满足姿态解算的速度要求。
无线收发模块选用 nRF905,GPS模块选用NEO-6M,二者均连接到STM32,使得开发流程高效有序。
数据存储模块SDRAM选用MT48LC16M16A2,容量256 MB,其含有16位数据总线,4个Bank,存储架构为 4 Banks×4 Mbits×16。 加入 SD 卡模块,用于存储飞行数据,便于上位机对飞行过程进行回放。
2.2 接口电路设计
FSMC是STM32系列采用的一种新型的存储器扩展技术,支持不同的外部存储器类型,其中包括多种类型的静态存储器[3],因此,可将FPGA当作STM32F407的外部SRAM来配置,通过扩展出的数据/地址/控制三总线来实现操作,这样既能保证较快的操作速度,又具有很高的灵活性[4]。接口硬件连接如图2所示。

图2 STM32与FPGA连接原理Fig.2 STM32 and FPGA connection schematics
将FPGA直接挂载到STM32的FSMC总线上,FSMC提供了 4个Bank用于连接不同的外部存储器,FSMC_NE1为Bank1第一区的片选信号,FSMC_NOE和FAMC_NWE分别为接口读写信号,根据设计的数据要求,设计数据位宽16位,地址位宽 10 位,将数据线 AD[15:0],地址线 A[25:16]连接到FPGA的I/O端口,还包括一些中断信号FSMC_NBL[0:1],用于 FPGA 向 STM32 发送中断请求。这样FPGA就作为STM32的外设接入,通过存储器读写指令访问FPGA。
在FPGA的数据接口设计当中,AD芯片的数据采集与FSMC总线的数据传输处于不同的时钟域,而数据在不同时钟域之间传递,容易产生亚稳态[5]。通过IP核设计异步FIFO用于数据的缓存与传输,采用2个时钟信号来控制其读写操作,分别为写时钟(wrclk)和读时钟(rdclk)。FIFO的模块框图如图3所示。其中异步FIFO模块包括8个端口[6],分别为数据输入(data[15:0])、写请求(wrreq)、写时钟(wrcl-k)、读请求(rdreq)、读时钟(rdclk)、缓冲器满信号(wrfull)、缓冲器空信号(rdempty)、数据输出(q[15:0])。

图3 异步FIFO的BlockFig.3 Asynchronous FIFO Block
2.3 数字滤波器设计
陀螺仪与加速度计均为模拟量传感器,其拥有较高的频率响应和高精度的测量数据,但其不可避免的会将电路中的噪声信号一同送往ADC芯片进行模数转换,这些噪声在数字系统的运算当中可能会被放大,影响测量精度,因此在FPGA内部创建数字滤波器,以进一步提高信噪比。
相比于完全依靠电阻、电容、晶体管等电子元件组成的模拟滤波器,数字滤波器具有更高精度、更高信噪比、无可比拟的可靠性等优点,虽然在其搭建过程当中工作量大、调试设计复杂,但其换来的灵活性与可扩展性可大大降低硬件电路板的设计及制作成本[7]。有限脉冲响应FIR(finite impulse response)滤波器由于其具有良好的线性相位和极高的稳定性,在数字信号处理领域得到了极为广泛的应用[8]。n阶FIR滤波器的输出y(n)可表示为输入序列 x(n)与单位取样响应 h(n)的线性卷积,如式(1)所示:

每一次的输出要完成N次的乘法和N-1次的加法,当阶数N较大时,系统延迟会很大。
根据传感器的输出特性和系统的数据传输需求,同时借助FPGA的高度并行和线性处理高速信号的特点,设计截止频率为20 kHz的31阶(长度为32)低通线性相位FIR滤波器,采样频率100 kHz,量化系数为16比特。为提高设计效率和系统可靠性,首先通过Matlab设计出滤波器系数,而后将其导入到Quartus II包含的FIR IP核当中,直接生成FIR模块。为获得更高的运算速度,选择全并行分布式算法结构[9],FIR滤波器系数设置如表1所示,FIR滤波器系数量化前后频谱如图4所示。

表1 FIR滤波器1~16阶系数设置Tab.1 FIR filter 1~16 order coefficient setting
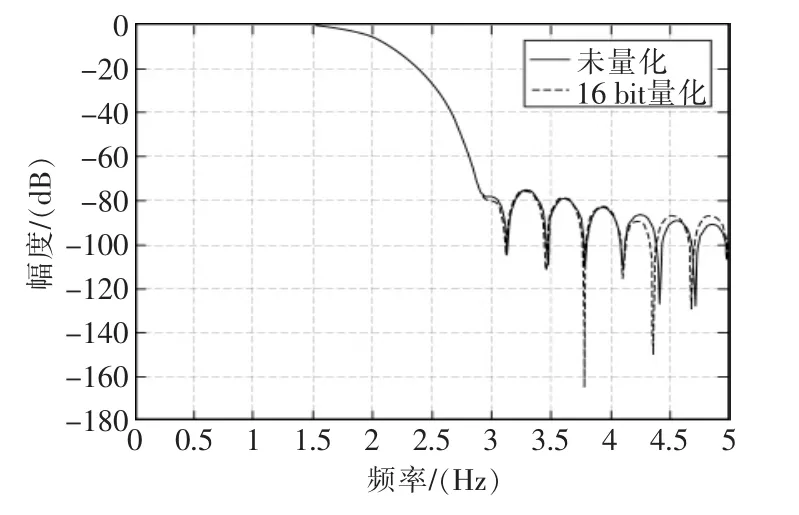
图4 FIR滤波器系数量化前后的幅频响应Fig.4 FIR filter coefficients are quantized before and after quantization
采用Matlab软件仿真出具有白噪声特性的输入信号,以及由10 kHz和30 kHz单频信号叠加的输入信号,进而仿真测试数据经滤波器滤波后的输出数据,以便和FPGA设计实现后的结果进行比较。Maltab仿真的信号滤波前后频谱如图5所示。
在FPGA设计完成后,编写Testbench文件,将仿真的输入信号作为ModelSim的激励源,生成经过FPGA滤波器的输出信号,对输出信号数据进行时域及频域分析,如图6和图7所示。
从图6可以看出,FPGA实现的滤波器输入、输出频谱与Matlab直接仿真的结果相同。从图7可以看出,滤波后的白噪声在时域上的变化趋势明显缓和,即滤除了高频分量,滤波后的合成单频信号已形成规则的频率为10 kHz的信号。因此,从仿真结果看,该滤波器的FPGA实现满足设计要求。

图5 Maltab仿真的信号滤波前后频谱图Fig.5 Matlab simulation of signal filtering before and after spectrum

图6 FPGA仿真的信号滤波前后频谱图Fig.6 FPGA simulation of the signal before and after filtering spectrum

图7 FPGA仿真的信号滤波前后的时域波形Fig.7 FPGA simulation of the signal before and after the time domain waveform
3 软件算法设计
3.1 飞行器姿态解算
该设计所选用的传感器都可以单独完成姿态角度的测量,但陀螺仪存在温度漂移误差,加速度计受机身振荡会产生测量白噪声,电子罗盘易受外部磁场的干扰,因此单个传感器很难得到相对准确的姿态角信息[10],为实时准确地获得飞行器的姿态角,采用卡尔曼滤波算法,将传感器所测数据进行融合,解算飞行器3个轴向的姿态角信息[11-12]。
卡尔曼滤波对数据的处理包括预测和更新2个过程。预测过程是通过前一时刻的状态估算现在的状态,更新过程是通过前一时刻的预测值和现在的观测值确定状态估测。不同的姿态估算方法具有不同的性能评估标准,卡尔曼滤波是以系统的最小协方差为标准。对于四旋翼飞行器系统,将系统连续信号离散化为计算机能处理的离散信号,令系统的采样周期为T,离散系统对应的状态方程X(k)和测量方程 V(k)如式(2)所示:
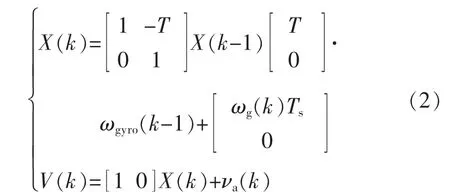
式中:ωgyro为陀螺仪输出的角速度;ωg为陀螺仪的测量白噪声;νa为加速度计和电子罗盘的测量白噪声。
需根据k-1时刻的角度值来估算k时刻的实际角度,再根据预测得到的k时刻的角度值得到k时刻的高斯噪声的方差,在此基础上卡尔曼滤波器进行递归运算直至估算出最优的角度值。系统的过程噪声协方差矩阵Q以及测量误差的协方差矩阵R 如式(3)所示:

式中:q_acce和q_gyro分别为加速度计和陀螺仪的协方差。该系统中陀螺仪的值更接近准确值,因此取q_gyro的值小于q_acce的值。
预测状态方程:
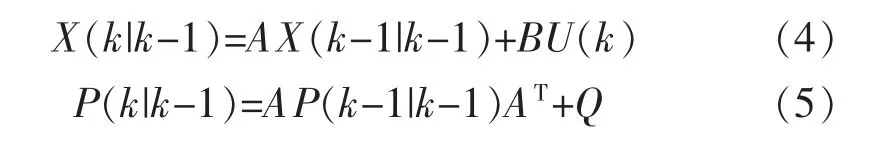
更新状态方程:
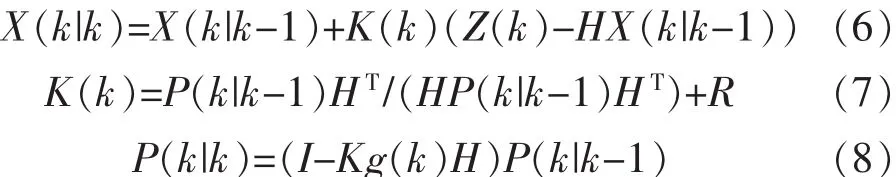
式中:X(k|k-1)为上一时刻状态预测值;X(k-1|k-1)为k-1时刻的最优值;X(k|k)为当前k时刻的最优估算值;P(k|k-1)为状态 X(k|k-1)的协方差;P(k|k)为状态X(k|k)的协方差;K为卡尔曼增益;I为单位阵计算完更新方程后,再次重复上一次的后验估计,作为下一次计算的先验估计,这样不断地循环运算直至找到最优结果。
3.2 飞行器PD控制设计
四旋翼飞行器的动力学模型特点为具有多入多出,带有强耦合的欠驱动系统,其动力学型表示如式(9)所示,式中[φ,θ,ψ]为飞行器的 3 个姿态的欧拉角,分别代表滚转、俯仰和偏航;[x,y,z]为飞行器质心在惯性坐标系中的位置;l为飞行器每个旋翼末端到飞行器重心的距离;m为飞行器的负载总质量;Ii为围绕每个轴的转动惯量;Ki为阻力系数。由于欠驱动特性的存在,不可能对所有的6个自由度都进行跟踪,一个合理的控制目标方案为跟踪航迹[x,y,z]和滚转角 φ,同时保证另外 2个角度。
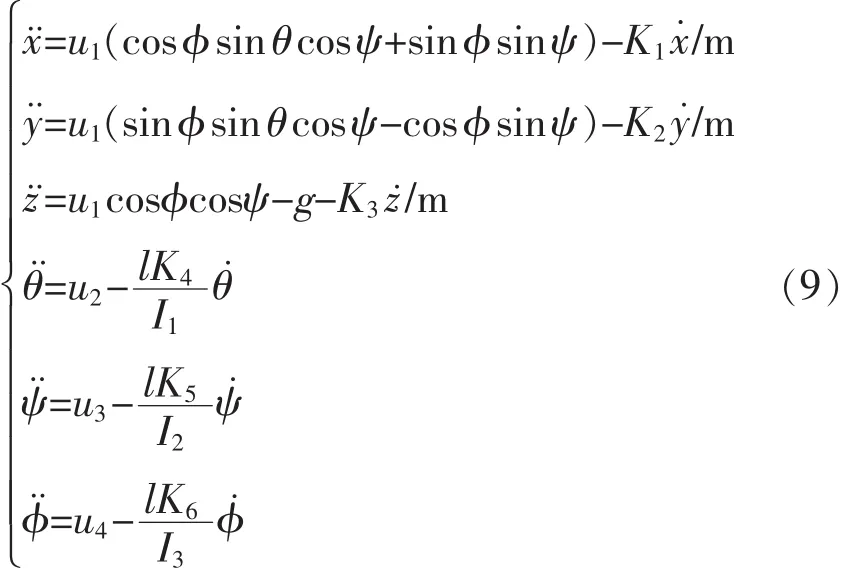
采用Matlab对控制系统进行仿真,通过输出波形评估该系统的稳定性,整个控制系统的结构如图8所示。
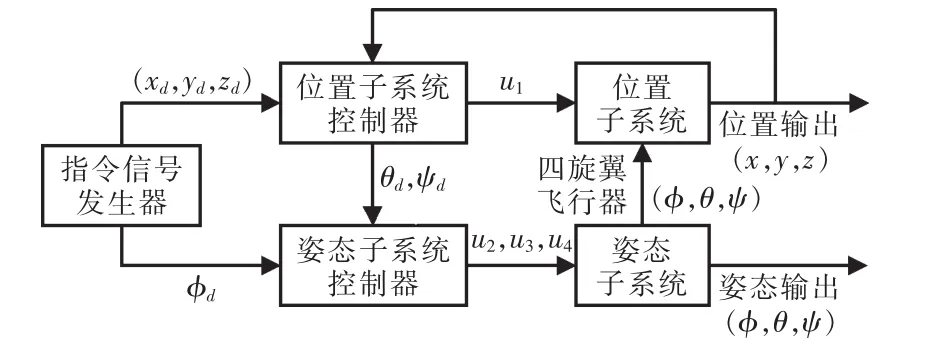
图8 闭环系统结构Fig.8 Closed-loop system structure

图9 三个位置状态的收敛过程Fig.9 Convergence of three position states
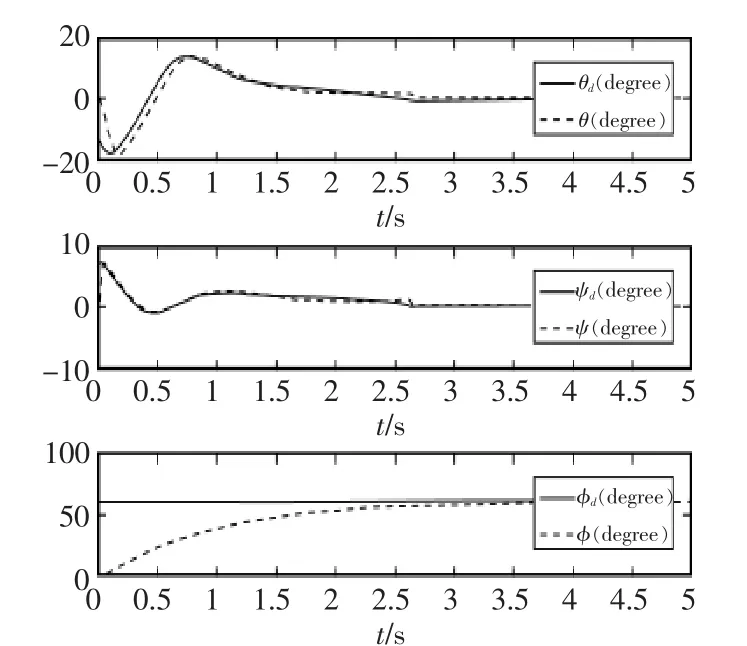
图10 三个姿态的收敛过程Fig.10 Convergence of three gestures
该控制系统属于由内外环构成的控制系统,采用双环控制方法设计控制律[13]。位置子系统为外环,姿态子系统为内环。在内外环控制中,内环的动态性能影响外环的稳定性,从而会影响整个闭环控制系统的稳定性。为实现收敛速度快的内环控制,采用内环收敛速度大于外环收敛速度的方法,以保证闭环系统的稳定性。在本算法中通过调整内环控制其增益系数,在设计中采用了较大的PD增益,保证内环收敛速度大于外环收敛速度。
针对模型式(9),设定微型四旋翼无人机相关参数[14]。 扰动取 d4=d5=d6=0.010,控制目标 x→0,y→0,z→zd,φ→φd,被控对象的初始状态取 [2 0 1 0 0 0],被控对象角度初始状态取[0 0 0 0 0 0],取 zd=3,φd=π/3。
仿真结果如图9~图11所示,分别为飞行器的位置、姿态收敛过程和4个控制输入的变化过程。
从仿真图9、图10可以看出,采用双闭环PD控制方式,在3 s的时候系统达到设定控制目标,进入稳态,且之后没有震荡,完全跟踪上期望值。从仿真图11可以看出,四个控制的输入大约在1 s之后完成控制的输入,虽然之后有小幅波动,但整体系统处于稳定状态,验证了该控制算法的可行性。

图11 四个控制输入的变化过程Fig.11 Four control inputs change process
4 结语
针对单一传感器测量四旋翼飞行器姿态角和位置信息的不准确问题,本文采用了多传感器采集飞行器数据,借助FPGA强大的数据并行处理能力,在保证数据实时性的基础上设计FIR数字滤波器,提高传感器数据的可用性,通过仿真验证了滤波器的可行性。在主控制器STM32上设计了卡尔曼滤波器用于多传感器的数据融合,进而对飞行器的姿态进行解算,结合四旋翼飞行器的动力学模型特点,设计了双闭环PD控制系统,并在Matlab下进行了相关仿真,仿真结果显示该控制算法响应速度快、稳定性好,为微小型四旋翼飞行器的设计奠定了基础。
[1]袁安富,徐金琦,王伟,等.基于双STM32多旋翼无人机控制系统设计[J].电子技术应用,2013,39(11):136-138.
[2]李侦,田梦君,赵菲菲.基于DSP的无人飞行器飞行控制系统设计[J].微处理机,2010,31(4):125-128.
[3]潘辉.STM32-FSMC机制的NOR Flash存储器扩展技术[J].单片机与嵌入式系统应用,2009,9(10);31-34.
[4]曹彬乾,程远增,杨青.基于STM32+FPGA的数据采集系统的设计[J].计算机工程与设计,2014,35(4):1231-1235.
[5]杨会建,田成军,杨志娟,等.基于FPGA的SDRAM乒乓读写操作设计[J].长春理工大学学报:自然科学版,2015(2):67-71.
[6]应进,潘浩曼,代冀阳,等.FPGA与ARM的无人机陀螺仪数据接口设计[J].电子技术应用,2014,40(1):9-12.
[7]杜勇.数字滤波器的MATLAB与FPGA实现-Altera/Verilog版[M].北京:电子工业出版社,2015.
[8]唐博,李锦明,李士照.基于FPGA的高阶FIR滤波器强抗干扰数据采集系统[J].电子技术应用,2012,38(9):89-92.
[9]李伟,武鹏飞,陈宏霖.基于DSP Builder的分布式算法的FIR数字低通滤波器设计[J].计算机应用,2015(S2):335-338.
[10]冯智勇,曾瀚,张力,等.基于陀螺仪及加速度计信号融合的姿态角度测量[J].西南师范大学学报:自然科学版,2011,36(4):137-141.
[11]吴友强,纪浩,邹力涵.基于卡尔曼滤波的四旋翼飞行器悬停控制研究[J].自动化与仪表,2013,28(11):1-5.
[12]万晓凤,康利平,余运俊,等.基于多传感器数据融合的四旋翼飞行器的姿态解算[J].科技导报,2014,32(19):31-35.
[13]刘金琨.先进PID控制MATLAB仿真.第4版[M].北京:电子工业出版社,2016.
