基于TW-TOF的UWB室内定位技术与优化算法研究

牛群峰，曹一帆，王 莉，惠延波

（河南工业大学 电气工程学院，郑州 450000）

基于UWB的定位技术有着精度高、功耗低、抗干扰能力强等优点，非常适合室内定位领域[1]。在导航制导以及目标定位跟踪领域，卡尔曼滤波作为最佳的线性滤波器被广泛使用[2]。本文使用DWM1000信号收发模块，采用基于双向飞行时间的测距方法并使用三边定位法构建UWB定位系统实现对室内移动人员的实时定位。对带有噪声干扰的定位数据使用IMM卡尔曼滤波对定位数据进行处理，并对处理结果进行分析。

1 UWB定位原理

UWB定位是基于测量距离的定位技术，其定位方法有TDOA、三边定位法等，测距的方法也是多种多样的[3]。本文采用的是基于飞行时间的双向测距方法TW-TOF测距，然后使用三边定位法计算坐标。

1.1 TW-TOF

基于飞行时间的双向测距方法TW-TOF是一种不需要通信双方时间同步的测距方法，避免了为获得时间同步增添的额外成本。这种测距方法要求基站和标签都具有信号收发功能，标签周期性的初始化距离测量信息，基站实时接收回复标签信号，并测量距离。具体步骤如图1所示。

图1 基于飞行时间的双向测距步骤Fig.1 Steps based on TW-TOF

当基站收到标签的轮询信息，基站记录此时的时间TRP，并发送回复信息给标签，并记录发送时间TSR。当标签收到回复信息后，记录接收时间TRR，并在 TSF时将标签记录的时间（TSP、TRR、TSF）发送给基站。基站获得标签发送的最终信息后获得足够的数据计算距离并进行以下计算：

（1）标签的信号往返延迟时间 TTRT=（TRR-TSP）减去这期间基站的反应时间得到 2次标签到基站的单程飞行时间tTA、tAT。

（2）基站的信号往返延迟时间 TART=（TRF-TSR）减去这期间标签的反应时间同理得到2次标签到基站的单程飞行时间。

之后，基站将上边求得的标签到基站的飞行时间求和并取平均值，得到单程飞行时间TOF。这样

TRSP跟不相同时，采用不对称双向测距以获得TOF计算结果：

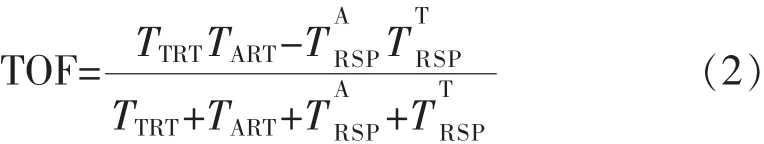
TOF乘以光速（UWB信号传递速度）便得到标签到基站的距离。

1.2 三边定位法

在通过TW-TOF等方法测得至少3个标签到基站的距离，在上位机或是基站使用三边定位法对标签的位置进行计算便可得到目标的位置坐标，如图2所示。

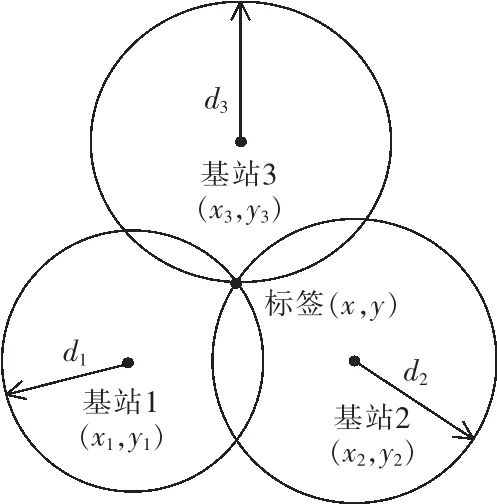
图2 三边定位法原理Fig.2 Principle of three sides location method

可以计算出唯一的交点作为标签点的位置。使用式（3）～式（6），根据测得的标签到基站的距离 di，可得到标签的位置（x，y）。

式（5）和式（6）中 di（i=1，2，3）为标签分别到 3个基站的距离。

2 卡尔曼滤波

通过TW-TOF测距可以算出标签到各个基站的距离，进而得到目标的位置。但在实际测量过程中由于非视距，多径传播以及人体等造成的随机干扰，导致观测到的信息中往往夹杂有随机噪声，造成观测到的定位的结果存在误差。卡尔曼滤波是最佳线性滤波器，实现简单，是纯时域的滤波器，被广泛使用在导航制导、目标定位和跟踪等工程领域[3]，并且其计算复杂度低，非常适合移动设备。使用卡尔曼滤波，利用上一时刻位置信息和本时刻的观测值对本时刻位置进行最优估计，被估计量随时间变化，这是一种动态估计。在目标跟踪中，不必知道目标的运动模型就能够实时地修正目标的状态参数如位置、速度等。

2.1 传统离散卡尔曼滤波器原理

用卡尔曼滤波获得最优估计值分为2个阶段。第一阶段使用上一时刻的信息对当前时刻的位置进行预测估计；第二个阶段，使用当前时刻的带有噪声的观测值对估计值进行修正。传统离散卡尔曼滤波器由以下5个公式组成。

式（7）为状态预测方程，对当前状态进行预测。式中矩阵At为状态转移矩阵，表示在没有噪声和控制量时2个连续时刻状态的关系；为当前状态的估计值；ut为t时刻的控制量，如在定位系统中为动力系统的加速度控制信号；矩阵Bt为控制矩阵，描述控制量如何作用于当前状态。式（8）为预测估计误差的协方差方程。式中Pt

式（9）、式（10）为状态更新方程和最优增益矩阵方程。式中为最优估计值；Kt为最优增益；为实际观测值与预期观测值的残差；H为观测矩阵。

卡尔曼滤波器最后一个方程为滤波误差协方差更新方程：

2.2 交互多模型卡尔曼滤波原理

试验中发现，传统卡尔曼滤波能有效降低做匀速直线运动定位目标的噪声干扰，得到理想的滤波效果。但当定位目标进行直角转弯或加减速这些室内常见动作时，仅采用基本的卡尔曼滤波会出现“滞后”等现象，短时间内造成较大的误差。这时需要自适应算法。交互多模型算法IMM使用2个或更多的模型来描述工作过程中可能的状态，最后通过有效的加权融合进行系统状态估计，很好地克服了单模型估计误差较大的问题。

IMM算法结构由5部分组成，如图3所示，包括计算模型混合概率、输入交互、对各模型进行卡尔曼滤波、模型概率更新以及输出交互[4]。

图3 IMM算法步骤Fig.3 Steps of IMM algorithm

2.2.1 计算模型混合概率

假定目标有r种运动状态，对应有r种状态转移方程。各模型之间的转移由马尔可夫概率转移矩阵确定，其中元素pij表示目标由第i个运动模型转移到第j个运动模型的概率，概率转移矩阵如下：

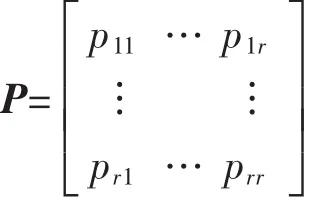
模型i到模型j的混合概率为

式中：μi（k-1）为上一时刻每个滤波器的模型概率；j为模型 j的预测概率（归一化常数），如式（13）所示：

2.2.2 输入交互

在这一部分，要重新初始化滤波输入，由上一时刻各模型估计与混合概率得到混合状态估计0j（k-1|k-1）和混合协方差估计 P0j（k-1|k-1），将混合估计作为当前循环的初始。对模型j，混合状态估计混合协方差估计方程可分别由式（14）～式（16）得到。式中：i（k-1|k-1），Pi（k-1|k-1）为上一时刻的状态估计与协方差估计。

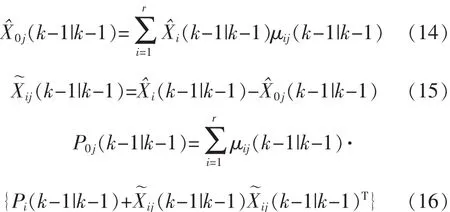
2.2.3 各模型卡尔曼滤波

这一部分，对不同的运动模型选择合适的卡尔曼滤波器进行滤波。

2.2.4 模型概率更新

模型概率计算是假设检验过程，即采用贝叶斯假设检验方法检验滤波器组各个滤波器的残差[5]。采用似然函数来更新模型概率μj（k），模型j的似然函数为

式中：vj（k）为滤波残差，如式（18）所示，Sj（k）可由式（19）得到：

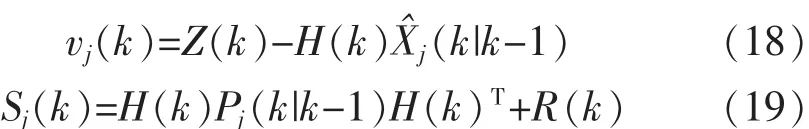
模型j的概率为

式中：c为归一化常数，如式（21）所示：

2.2.5 输出交互

由第四步获得更新的模型概率后，输出交互，对每个滤波器的估计结果加权合并，得到总的状态估计（k|k）和总的协方差估计模型 P（k|k）。

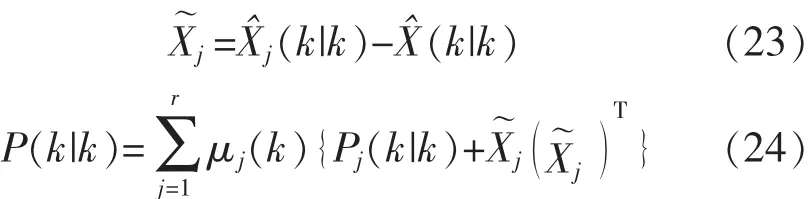
3 试验分析

3.1 试验设计

在室内环境中，定位目标经常要进行90°直角拐弯，本文对此要求在室内环境设计了路径试验对比检验传统卡尔曼滤波与IMM滤波效果。首先，使用3基站1标签采集定位数据。基站按三角形分布在（0，0），（0，3.8），（5.6，2.2）3 个空间固定坐标位置。试验人员按设定路线从（0，1.4）开始沿x轴正方向运动4.8 m后转90°沿y轴正方向运动2.4 m后再转90°沿x轴负方向运动4.8 m（由于标签由试验人员手拿采集数据，得到的位置与预定轨道有一定的偏移），如图4所示。试验的采样周期为0.1 s，在基站A0（0，0）处用USB数据线连接电脑通过串口调试助手对标签到3基站的距离数据进行采集。使用式（3）～式（6）计算出所有坐标，并进行卡尔曼滤波。传统卡尔曼滤波与IMM卡尔曼滤波效果如图5所示。并对传统卡尔曼滤波和IMM卡尔曼滤波做RMS分析，得到其误差跟踪图，如图6所示。

图4 基站布置以及标签移动路径Fig.4 Base station layout and label moving path

图5 传统卡尔曼与IMM滤波观测值轨迹和轨迹Fig.5 Observation trajectory and trajectory of traditional Kalman and IMM filtering

图6 传统卡尔曼与IMM滤波误差跟踪图Fig.6 Traditional Kalman and IMM filtering error tracking map

3.2 试验结果分析

从图5可以观察到，在沿x轴运动初期，卡尔曼滤波对目标误差消除作用是非常明显的，其曲线相比于观测值更加平滑。但在x轴向y轴转向和y轴向x轴两次90°转向之后的过程中，卡尔曼滤波值相对于观测值都产生了“滞后”的现象，造成短时间内误差值甚至大于观测值。传统卡尔曼滤波由于是建立在模型精确和随机干扰信号统计特性已知的情况下，在卡尔曼滤波整个过程中干扰信号的统计学特征值保持不变[6]。然而，试验人员在转弯时突然的加速与减速使得干扰信号统计学特性发生了改变[7]。交互多模型采用多个卡尔曼滤波器并行处理，每个滤波器对应不同的状态空间模型，不同的状态空间模型描述不同的目标运动状态，最后通过有效的加权融合进行系统估计，很好地克服了传统卡尔曼滤波单模型估计误差较大的问题。如图5所示，在第一次y轴向x轴90°转向之后，传统卡尔曼滤波会逐渐恢复其功能，但短时间内会造成极大的误差，如图上第一次x轴向y轴转向，x轴方向上的误差最大接近50 cm。IMM滤波虽然在第一次转弯的时候也产生了“滞后”现象，但相比较传统卡尔曼滤波，其造成的误差更小，并且收敛的速度明显快于传统卡尔曼滤波。并且从图6传统卡尔曼滤波与IMM滤波的误差跟踪图中可以明显看出，IMM的滤波效果要优于传统卡尔曼滤波。

4 结语

采用UWB技术的室内定位有着精度高、功耗低、传输速率快、抗多径干扰能力强等优点，目前基于UWB技术的定位多采用基于测量距离的定位方法[8]。本文介绍了基于飞行时间的双向测距方法（TWTOF）的过程。对于室内环境中干扰多以及传统卡尔曼滤波在目标机动时滤波效果不好的特点，本文提出使用交互多模型卡尔曼滤波的方法对定位坐标进行最优估计以降低误差，并针对室内环境设计了试验检验其效果。试验结果显示，交互多模型卡尔曼滤波能有效的减少误差，在室内环境经常遇到的大转角情况下，卡尔曼滤波效果虽然在短时间内仍会产生误差，其滤波值误差要高于观测值，但其能更加快速的恢复滤波效果。总体上，交互多模型卡尔曼滤波对观测值的优化效果十分显著。

[1]杨洲.基于UWB/MEMS的高精度室内定位技术研究[D].徐州：中国矿业大学，2015.

[2]张桀，沈重.联合TDOA改进算法和卡尔曼滤波的UWB室内定位研究[J].现代电子技术，2016，39（13）：1-5.

[3]邵磊.基于超宽频距离传感器的室内定位系统的研究与实现[D].北京：北京工业大学，2014.

[4]王磊，程向红.基于期望模式修正的交互多模型组合导航算法[J].光学精密工程，2014，22（3）：737-744.

[5]Pelka M，Goronzy G，Hellbrück H.Iterative approach for anchor configuration of positioning systems[J].Ict Express，2016，2（1）：1-4.

[6]Zhang R，H?flinger F，Reindl L.TDOA-Based localization using interacting multiple model estimator and ultrasonic transmitter/receiver[J].IEEE Transactions on Instrumentation&Measurement，2013，62（8）：2205-2214.

[7]Hu C，Chen W，Chen Y，et al.Adaptive Kalman filtering for vehicle navigation[J].Journal of Global Positioning Systems，2003，2（1）：42-47.

[8]Abdulrahman A，Abdulmalik A S，Mansour A，et al.Ultra wideband indoor positioning technologies：analysis and recent advances[J].Sensors，2016，16（5）：1-36.