一种机器人六维腕力传感器的标定方法
2018-03-30郑朝阳翟其建赵金鹏
郑朝阳,翟其建,赵金鹏
(中国船舶重工集团公司第七一六研究所,连云港 222006)
对于机器人腕力传感器来说,由于结构复杂、加工误差以及弹性体结构质地的不均匀性等各方面因素的影响,使得传感器各输出通道之间存在相互耦合,这种耦合的关系很复杂,难以从理论上进行精确的描述[1],需要采用试验的方法来进行标定。标定不但可以对传感器进行定度,还能检验设计正确与否。本文介绍了腕力传感器的标定原理,并用试验的方法对一种腕力传感器进行了标定,对标定结果进行了试验验证,并对标定误差进行了分析,结果显示该标定方法有效,传感器设计合理,标定误差在可接受范围内。
1 腕力传感器标定方法
目前大部分腕力传感器是通过测量弹性体的形变来得到其六维力和力矩的[2]。本文将弹性体上应变片组成电桥来得到输出,对腕力传感器进行标定的关键就是建立传感器的六维力和力矩的输出与贴应变片处应变的关系。
假设传感器应变片的六维输出电压为V=(Vfx,Vfy,Vfz,Vmx,Vmy,Vmz), 它们分别与受力后相关的应变片的阻值变化量的绝对值成正比,而由应变片的工作原理可知,应变片变形后的阻值变化正比于贴片处的应变。假设传感器在力负载范围内是线性的,即在定常系统条件下,输入力和输出电压之间存在如下关系式:

式中:F∈R6×1为作用在传感器弹性体上的力和力矩;V为相应输出电压;C为常数矩阵即为标定矩阵。
一般来说,传感器的标定就是求标定矩阵C,也就是根据加载在传感器上的已知力F(标定力)和传感器六通道的电压输出值V,由式(1)求解出矩阵C;C已知后,在传感器上施加任意方向大小的载荷,就可以根据输出电压V得到传感器上加载的力F的大小。
本文中腕力传感器为十字梁型,其弹性体包括底座、中心台、主梁和浮动梁等。弹性体4个主梁的上下及2个侧面均粘贴有应变片,共16个应变片,该应变片与固定电阻电桥相连以获取六维电压分量。弹性体上坐标及应变片分布如图1所示。

图1 弹性体上坐标及应变片分布Fig.1 Distribution of coordinates and strain gauges on elastic body
腕力传感器在各个力加载后,弹性体相应部位的变形引起应变片阻值的改变,将应变片采用相应的全桥电路连接[3],即可得到电压信号的变化,接着对信号进行放大等处理得到可稳定测量的电压信号,此时就建立了电压与力之间矩阵的关系,根据式(1)即可得到标定矩阵C。
假设 Rfx、Rfy、Rfz、Rmx、Rmy、Rmz分别表示受力 Fx、Fy、Fz、Mx、My、Mz作 用 时 相 应 应 变 片 变 化 量 的 绝 对值。R1、R2、R3……R16为应变片受力变形后的阻值,应变片初始阻值。设各维力和力矩方向都为正方向,根据应变分析,则有下列公式:

各应变片组桥如图2所示,共8个,即为8路电压输出,其中为阻值相同的固定电阻,E0为外部稳压电源。各桥路输出电压的表达式如式(3)所示,获得以上8路电压后,对其做如下处理,即可得如下所示的六维分量的输出电压表达式。

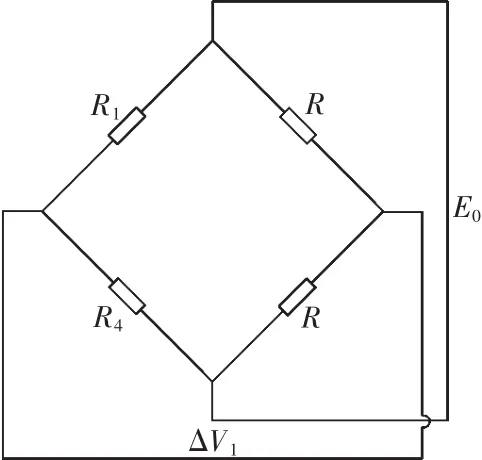
图2 应变片组桥示意Fig.2 Schematic diagram of stain gauge bridge
从上式可以看出,由采集到的6路电压信号变换得到对应的6路电压信号,此间对电桥电路进行调零、温补,经过加法器、电阻解耦、运算放大等,将8路信号做模拟运算形成六维力对应的六路电压信号输出,再由式(1)计算出标定矩阵,即完成腕力传感器的标定。
2 腕力传感器标定试验
2.1 腕力传感器解耦的基本方法
由于结构、制造工艺和检测等方式上的原因,几乎每一个作用到腕力传感器上的力分量都会对传感器其他各路输出信号产生影响,这就是所谓的耦合。耦合会使得测量精度下降,要消除或抑制耦合的影响,应该从两方面入手:第一是设法消除其产生的根源,这涉及到传感器制造工艺和现阶段的加工条件等诸多问题,往往难以解决,同时又会增加传感器的制造成本;第二是利用标定矩阵,采取模拟或数字信号处理的方法来消除传感器维间耦合[4-6]。由于这种相互藕合的关系比较复杂,难以从理论上进行精确的描述,故采用第二种方法,即采用试验的方法来进行标定,这样既能降低对腕力传感器制造工艺的要求,又能获取较准确的测量结果。
解耦之前,首先做如下假设:①任何输入的作用力都可以化为假定坐标系中的六维分量;②输出电压矢量对应整个传感器的输出空间,即有输入就有输出;③输出电压可以进行线性叠加;④腕力传感器的装配稳定可靠(不产生滑动)[7-9]。
在式(1)的运算过程中,也就完成了腕力传感器的维间解耦。求解C的问题就等价于求解线性方程组的问题。线性方程组解的精度越高,C的精度也就越高[10]。标定矩阵是利用试验方法测得的,通过对传感器加载已知的单维力,可以从各个电桥电路获得相应的电压输出,根据式(1)求出其传递系数矩阵(标定矩阵):

2.2 腕力传感器标定的试验装置及方法
腕力传感器力加载方式主要有测力环式和砝码重锤式2种[11],由于试验设备所限,本课题采用砝码重锤式加载方法。力加载装置如图3所示。腕力传感器安装在加载帽里,受力柱穿过传感器中轴,加载帽固定在带有刻度的可旋转的分度盘上面。试验台的左右滑轮是可以上下调节的,在水平方向上呈一条直线,与y轴重合。重锤式加载采用拉力方式,力值精度比较高。使力作用线通过传感器变形中心,即可获得纯力(如单维力),如要获得纯力矩,则应该加力偶于传感器。加载步骤为
步骤1 对传感器进行X方向的加载试验时,首先要将分度盘旋转一定的角度,使得传感器的X轴方向与试验台的水平方向重合。接着通过滑轮以此增加砝码,完成X轴正方向加力;再将分度盘旋转180°,重新以此增加砝码,完成X轴负向加力。
步骤2 对传感器进行Y轴方向的加力试验方法与X方向基本相同,只是自原来测X正方向时刻度盘位置逆时针旋转90°。
步骤3 测量Z轴负方向力时,可直接将砝码加载到加载帽上;测量正方向时,要将加力绳子绕过附加的滑轮杆直接连接到右边滑轮上,通过此滑轮以此加载砝码。
步骤4 对Mx正方向加力矩的方法如图3所示,在左右滑轮两侧加大小相同的砝码;测负方向力矩时,应该将左右滑轮移动相同高度,并且方向相反,接着加载砝码。

图3 加载试验台示意Fig.3 Schematic diagram of loading test table
步骤5 测My方向力矩与Mx方向相同,只是要将分度盘旋转90°。
步骤6 对Mz方向力矩进行测量时,将加力绳分别固定在2个受力柱上,接着旋转分度盘,
使得受力柱的连线与Y轴垂直,此时受力轴之间的距离就等于力臂值。调节滑轮与受力柱使其在同一高度,分别在两边加相等砝码,即可测量Mz正方向的力矩。负方向力矩的测量由于左右滑杆在试验台上位置固定而无法进行加载试验,对试验会有所影响,不过由于弹性体的对称性,其对标定结果影响有限。
为了获得较高的标定精度,在传感器进行标定时通常选取6个线性无关的力向量组成标定力。六维腕力传感器的标定流程如图4所示。
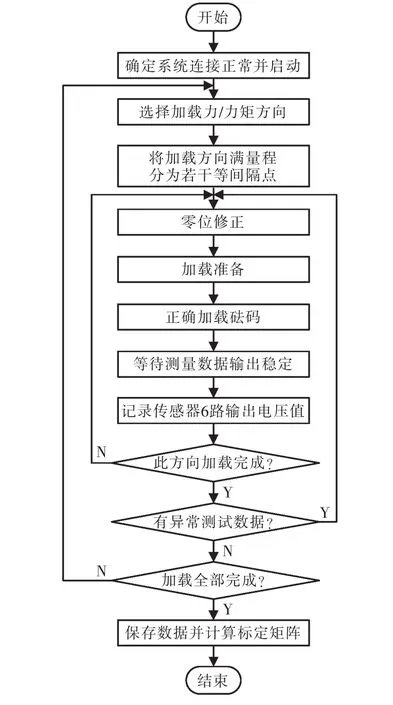
图4 传感器的标定流程Fig.4 Calibration flow chart of sensor
依次给传感器施加 6 个方向(Fx、Fy、Fz、Mx、My、Mz)的标定力,对各个通道的模拟电压信号进行测量,为减小随机误差的影响,测量值取各通道测量值的平均值,可得一个数组,从而获得加载矩阵F和对应的输出电压矩阵V。
2.3 传感器标定结果及数据分析
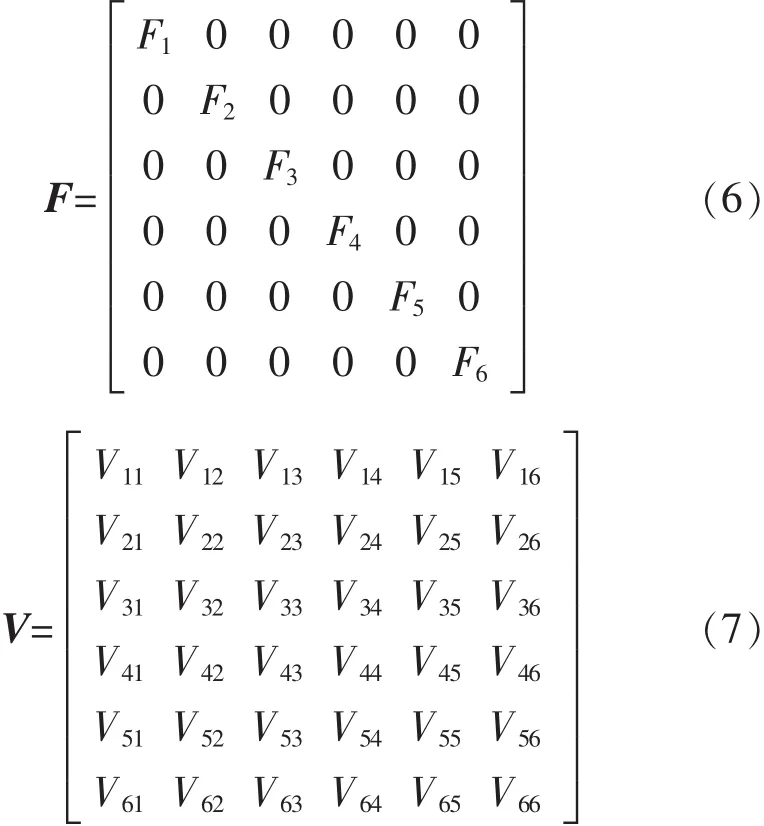
根据标定流程进行标定试验后,获得多组如式(6)与式(7)所示的矩阵 F 与 V 后,由式(5)求解出标定矩阵C为

通过对矩阵C的分析可知,C矩阵非主对角元素不为零,这是由于传感器存在维间耦合作用,在加载单位力/力矩时,对其他方向的力与力矩产生了干扰作用。矩阵C中C15与C42相对较大,稍微接近主对角元素,这说明了My对Fx、Fy对Mx的影响相对于其他分量要大一些。但这种影响也只在12%以内,对传感器最终的影响有限。
在得到了单维力逐步加载后的相应电压数据后,把测量数据在Matlab中进行线性拟合[12],各维力的力/力矩值与输出电压信号的拟合直线如图5所示。
从上图可以看到,各原始数据线性度较好,且基本上都关于零点对称,说明腕力传感器各方面设计结果较好,达到了预期的效果[13]。
2.4 对标定矩阵C的验证试验
得到标定矩阵C后,为验证其正确性,本文采用以下3种情况来对其进行试验的验证:①传感器量程内的单维力,取Fx=-10 N;②传感器量程内的单维力矩,取Mz=50 N·mm;③力与力矩组合的情况,加力设置Fx=-10 N,Mz=50 N·mm 。表1列出了理论输出与试验输出(即试验电压信号输出结果经标定矩阵处理后)的结果对比。

图5 单维力/力矩作用下对应输出电压拟合直线Fig.5 Single axis force/torque corresponding to the output voltage of linear fitting

表1 对矩阵C进行验证试验结果和理论结果对比Tab.1 Matrix C is validated by comparing experimental results with theoretical results
由上表可以看出,无论是在对单维力或力矩或是对较为复杂受力情况的标定中,由标定矩阵C都能得到与理论输出相对符合的结果。这说明标定矩阵C是符合要求的。
3 标定误差分析
由于腕力传感器标定方法与标定装置比一般的单维力传感器复杂很多,其误差也更加多样化。总体来说,系统误差大致分静态非线性率(Ⅰ类误差)和静态耦合率(Ⅱ类误差)两类来处理[14]。
对于以上两类误差的产生的原因,可归纳为以下3个方面:
(1)电压信号测量系统的放大电路等的漂移,以及各种外界干扰因素带来误差。该类误差可以通过优化电路板的设计、运用更高精度的运放及采取屏蔽接地等抗干扰措施来降低其对系统的影响。
(2)施加标定力的不准确性。这其中包含砝码误差、力传递过程的摩擦力产生的误差、还有悬挂砝码的绳索的自重的误差等。a.砝码误差。本次采用Ⅳ级砝码来施加标定力,根据砝码允许的误差标准,其相对范围误差为ew≤0.01%;b.力传递过程中摩擦力产生的误差。由于滑轮与绳之间不光滑,会存在一定程度的滑动摩擦;c.绳索自重产生的误差。绳索尽量采用柔软的棉线材料,这样自重引起的误差会降低到最小程度。
(3)施加力方向和位置误差。理想的情况下,加载力的作用线应通过传感器的坐标原点,但我们在实际的作用力是加载在加载帽上的,与理想情况有所差别。另外,受制造、装配及零部件变形等因素影响,会引起加力点与加力方向与理想位置发生偏差。故进一步控制位置偏差,误差还可进一步降低。
总之,误差的产生是标定试验中的必然结果,但大部分误差都可以通过我们的分析和改进来降低其影响,尽量减少可控制的误差。由于各种条件的限制,本课题的两类标定误差总范围控制在10%以内,基本满足要求。
4 结语
本文介绍了腕力传感器的标定原理和标定试验所需的主要硬件组成,对标定力矩阵的力向量的数目进行了探讨,结合实际,对本课题传感器标定的方法进行了详细的说明。接下来进行了传感器标定的试验,列出了详细的标定流程,根据试验结果,得到了标定矩阵,并运用Matlab对各单维力/力矩的试验结果进行了处理,线性化较好,接着对标定矩阵C进行了验证试验,效果达到预期的要求。最后对标定过程中的误差进行了分析与总结,提出了进一步减小误差的方法。
[1]姚建涛,李立建,许允斗,等.超静定六维力传感器静定测量模型及标定方法[J].仪器仪表学报,2013,34(9):1927-1933
[2]郁有文,常健,程继红.传感器原理及工程应用[M].西安:西安电子科技大学出版社,2002.
[3]陈艳红.传感器技术及应用[M].西安:西安电子科技大学出版社,2013.
[4]曹会彬,孙玉香,刘利民,等.多维力传感器耦合分析及解耦方法的研究[J].仪器技术学报,2011,24(8):1136-1140
[5]Jianhe Lei,Liankui.Application of neural network to nonlinear static decoupling of robot wrist force sensor[C]//Proceedings of the 6th World Congress on Intelligent Control and Automation,2006:5282-5285.
[6]Jiang Zhaohui,Kohno M R.Robotic manipulation of flexible objects based on vibration control using force sensors[C]//2002 IEEE International Conference on Systems,Man and Cybernetics,Hammamet,Tunisia,2002:4-6.
[7]马俊青,宋爱国,吴涓.三维力传感器静态解耦算法的研究与应用[J].计量学报,2011,32(6):517-521.
[8]肖汶斌.六维力传感器静态解耦算法[M].武汉:海军工程大学学报,2012.
[9]MA Junqing,SONG Aiguo,XIAO Jing.A robust static decoupling algorithm for3-axisforce sensorsbased on coupling error modeland ε-SVR[J].MDPI.Basel,Switzerland.October,2012,12(11):14537-14555.
[10]郑红梅,仇成群.机器人六维腕力传感器静态标定系统的研究[C]//安徽制造业发展博士论坛,2004.
[11]武秀秀,宋爱国,王政.六维力传感器静态解耦算法及静态标定的研究[J].仪器技术学报,2013,26(6):851-856.
[12]吴涓,曹效英,宋爱国,等.Matlab在腕力传感器系统标定中的应用[J].传感技术学报,2001,14(3):177-182.
[13]何小辉,蔡萍.一种小量程六维力传感器的设计与分析[J].传感器与微系统,2012,31(1):20-25.
[14]费业泰.误差理论与数据处理[M].4版.北京:机械工业出版社,2004.
