基于RBF神经网络的翻曲机器人自适应滑模变结构控制

周军超 ，田建平 ，汤爱华

（1.四川理工学院 机械工程学院，自贡 643000；2.人工智能四川省重点实验室，自贡 643000）

在白酒制曲车间自动化生产线逐步实施阶段，针对曲房的搬运以及翻转的自动化设备仍处于研制状态[1]。由于该搬运翻曲机器手为悬挂式，因此在高速重载的情况下，机器手抖动严重[2-3]。

随着机器人技术的发展，在白酒酿造过程中采用了机器人翻曲替代人类劳动[4]。对于机器人控制的研究很多，但是从运动规律方面考虑的文献较少。已有的研究均从运动曲线的几何平滑性方面考虑，并未结合机器人的结构、材料及运动的实际情况，只是进行运动学的推导分析而未进行动力学分析。对此，文中以翻曲机器人为例，从动力学角度出发，结合机器人部件结构、材料和运动实际情况，对翻曲机器人进行动力学分析；在动力学分析的基础上，将神经网络与滑模变结构控制相结合，对翻曲机器人运动的抖振以及稳定性进行研究。

1 翻曲机器人动力学

针对四川某白酒大曲制区车间曲块在曲房内的发酵工艺，在发酵过程中一般需要进行2次翻曲。曲块的尺寸为100 mm×100 mm。整个机械手负载30 kg。其本体结构主要为腰部关节、臀部关节、夹持关节。翻曲机械人的本体结构如图1。

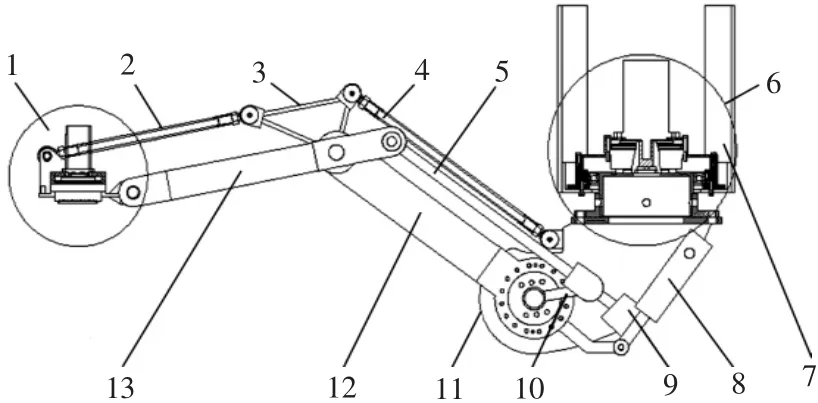
图1 翻曲机器人本体结构Fig.1 Body structure of turn over robot

2 RBF神经网络自适应滑模变控制

2.1 系统描述

被控对象为

对于n关节的机器人，若考虑摩擦力、未建模态和外加扰动的影响，利用拉格朗日方法，可以得到其动力学方程为

式中：f（·）和b为未知；fd为外加干扰信号；u为控制信号输入。

则有：

式中：Mn，hn（θ，）为确定量。

2.2 基于线性反馈的滑模变结构控制

机器人轨迹跟踪的目的是使实际的运动控制能够更好使得跟踪期望的轨迹xd。设位置指令xd，跟踪误差e为

定义滑模面为

根据线性反馈，将滑模控制律设计为

对于系统模型的控制采用状态反馈方法，不确定部分采用RBF网络状态进行线性反馈补偿器。基于上述控制方法实现了外部扰动、参数变化等不确定性的鲁棒性控制。

2.3 RBF神经网络的自适应学习

神经网络具有较强的全局逼近能力，由输入层、隐含层和输出层3部分构成，其结构如图2。

图2 RBF神经网络结构Fig.2 RBF neural network structure

在工程应用中，模型不确定性f未知，因此需要对不确定项进行逼近。

RBF神经网络的基本思想是采用径向基函数作为隐含层，广义RBF网络即从输入层到隐藏层相当于把低维空间的数据映射到高维空间，输入层细胞个数为样本的维度，所以隐藏层细胞个数一定要比输入层细胞个数多。RBF网络能够逼近任意的非线性函数，可以处理系统内难以解析的规律性，具有良好的泛化能力，并具有很快的学习收敛速度，已成功应用于非线性函数逼近、时间序列分析、数据分类、模式识别、信息处理、图像处理、系统建模、控制和故障诊断等[5]。

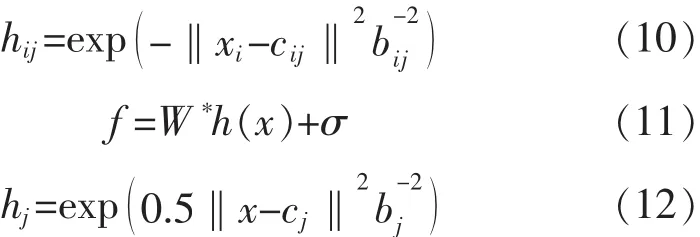
式中：x为网络的输入；j为网络隐含层第j个节点；W*为网络的理想权值；σ为网络的逼近误差，σ≤σN。

2.4 稳定性证明

在此，验证RBF神经网络自适应滑模控制的稳定性。考虑神经网络存在建模误差τd和函数逼近误差σ的情况，其中定义李雅普诺夫稳定性函数为

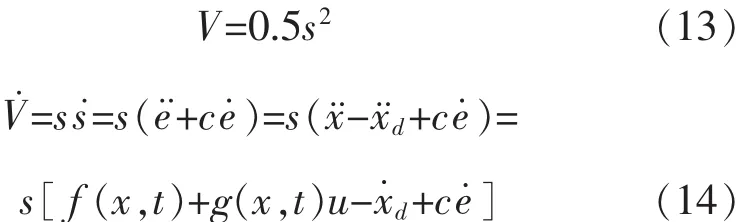
则

由此可见，所设计的基于RBF的滑模控制器是稳定的。

3 仿真实例

为了验证控制算法的有效性，以翻曲机器人的末端关节作为被控对象，Matlab与Adamas进行联合仿真试验。滑模变控制的参数设置为，Kv=dig｛50，50｝，Λ＝diag｛5，5｝；在鲁棒项取 ζn=0.2，ζd=0.1。设定参数后进行仿真，仿真结果如图3所示。

由图 3（a）、3（b）可见，文中所提算法具有良好的位置跟踪能力和收敛速度；图 3（c）、3（d）可见，控制输入变化缓慢，这说明抖振现象得到明显的改善。

4 结语

针对酿酒翻曲机器人运动中抖振和控制存在的不确定性等问题，文中从动力学角度出发，提出了基于RBF网络的线性反馈滑模变控制策略。该模型结合机器人部件结构、材料和运动等情况，通过仿真实验可知，该方法具有良好的控制精确度，同时有效削弱了抖振。

图3 基于线性反馈的滑模变控制算法仿真结果Fig.3 Simulation results of sliding mode variable control algorithm based on linear feedback

[1]任毅，东童童.“智能制造”对中国食品工业的影响及发展预判[J].食品工业科技，2015，36（22）：32-36.

[2]Meilgaard M.Effects on flavourofinnovations in brewery equipment and processing：a review[J].Journal of the Institute of Brewing，2001，107（5）：271-286.

[3]谢亮亮，田建平，杨海栗，等.悬挂式搬运翻曲机器人刚柔耦合动力学分析[J].食品工业，2017，38（5）：230-234.

[4]田建平，谢亮亮，杨海栗，等.悬挂式翻曲机器人关键构件优化研究[J].食品工业，2017，38（2）：219-224.

[5]曾丽娟，孙杰.基于RBF的水果采摘机器人关节伺服自适应滑模控制[J].农机化研究，2017，39（9）：207-211.