大直径顶管近距离侧穿高架桥桩的数值分析

王谭 安关峰

（1.广州市市政集团有限公司 510060；2.广州市市政集团市政工程技术研究院 510060）

引言

顶管技术作为一种非开挖地下管道铺设的施工技术，近年来得到了快速发展［1］。然而，随着工程建设的规模愈来愈大，顶管施工难免会穿越高架桥，由于顶管的掘进对桥桩周边土体产生扰动作用［2］，继而改变了桩基周边土体的应力状态，从而诱发桥桩位移，可能影响高架桥的正常使用，严重时甚至危及高架桥的安全。

目前，隧道临近桥桩施工对桥桩影响的研究方法主要有理论分析和数值分析：张云军等［3－6］开展了隧道开挖对邻近桩基的数值分析，研究了隧道开挖引起的桩基附加内力与变形及其影响因素；李早等［7］采用两阶段理论分析法评价了隧道施工对桩基内力与变形的影响；毛海和［8］对杭州污水管顶管施工土体扰动理论进行了分析，同时结合大量工程进行了顶管施工中土与结构性状的研究。由于顶管与桩基相互作用体系的复杂性、岩土介质的差异性及实际工程的特殊性，采用数值分析方法能较为全面和简便地模拟隧道施工过程。

基于此，本文在已有研究成果的基础上，借助MIDAS-GTS有限元软件，以广州市石井河污水处理系统工程为依托，建立了顶管工作井开挖及顶进过程中的计算模型，探索隧道开挖对临近高架桥桩的影响规律，且与现场实测数据对比分析，得到一些有益的结论，以期为类似工程提供借鉴。

1 施工扰动机理分析

对于顶管施工而言，其力学行为是隧道掘进与周围地层相互作用的结果，不能割裂两者之间的联系。在大型顶管施工过程中，开挖面的掘进、土体输出、工具头的顶进、平衡泥浆（或气体）的注入等均会产生应力扰动，顶管施工扰动主要包括三个阶段：（1）初始应力平衡阶段，在顶管开挖扰动前，土层处于应力平衡状态；（2）开挖应力扰动阶段，顶管接近与通过时，土层经历挤压隆起、损失松动，出现明显的变形，并向周围扩散衰减；（3）注浆变形稳定阶段，随着注浆的注入与硬化，阻止了土层塌陷与松动的发展，扰动后变形趋于稳定。顶管前方在正面顶进力的作用下处于被动状态，扰动面倾角为45°－φ／2，而管节环向外围土层因空隙的存在表现为主动状态，所以扰动面倾角为45°＋φ／2，具体如图1所示。

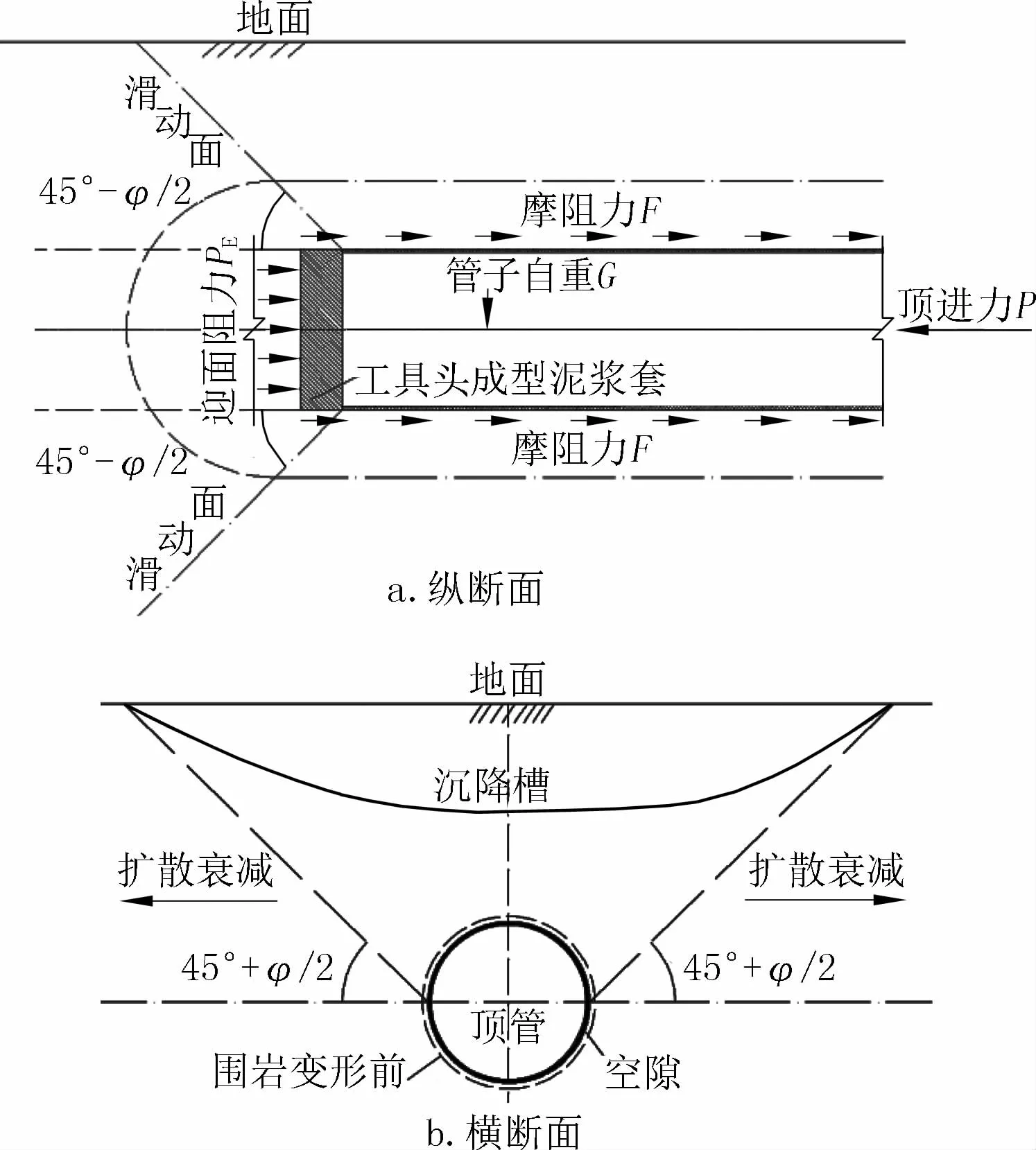
图1 顶管施工土体扰动效应Fig.1 Disturbance deformation of ground

顶管施工与盾构法相应的施工工艺非常类似，因此这两种施工方法对地层的扰动有相似的机理、扰动区土体变形及特性。假设地面下沉槽体积等于地层损失体积与土体密实变化产生的体积增量之和，顶管施工引起的地表沉降横向分布计算公式［9］为：

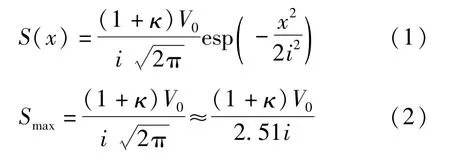
式中：S（x）为地表沉降量；V0为地层损失量；κ＝V1／V0，V1为扰动区土体密实度改变产生的体积变化量；x为距管道中线的水平距离，i为宽度系数；Smax为x＝0时出现的最大沉降量。

2 数值计算模型

2.1 工程简介

广州石井河污水处理系统工程位于华南路三期工程B1标段平沙互通立交桥的正下方，其中顶管段垂直下穿高架桥主桥或匝道，对主桥29＃和30＃桥墩及M匝道8＃和9＃桥墩、O匝道5＃和6＃桥墩产生不利影响。

顶管外壁距离桥梁桩基外壁最近约4m，紧邻的FDW02工作井外壁距离桩基外壁的最小水平净距约6.8m，顶管与高架桥桩的位置关系示意见图2、图3。该工程通水管道采用直径为3000mm的钢管，管道埋深约为9.5m，FDW02工作井采用逆作拱墙的施工工艺，开挖深度14m，内径11m，在周边采用旋喷桩加固地层并起到止水帷幕的作用。

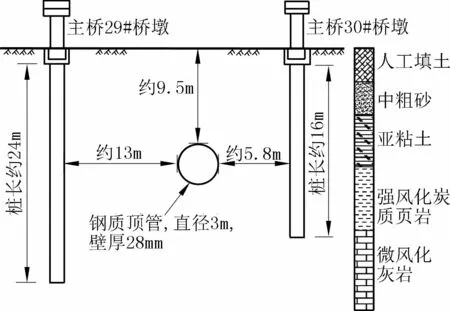
图2 顶管与高架桥桩的位置Fig.2 The position of pipe jacking and viaduct pile

根据项目地质勘查报告可知，高架桥桩基从上至下依次穿越砂层、粘土层、残积土层、全风化、中风化和微风化岩层，桩基嵌入微风化岩层内，而顶管管道穿越地层主要为砂层与残积土层。顶管及桥梁桩基所在土层物理力学参数见表1。表2为触变泥浆中管壁与土的平均摩阻力取值［10］，本工程顶管取 6kN／m2。

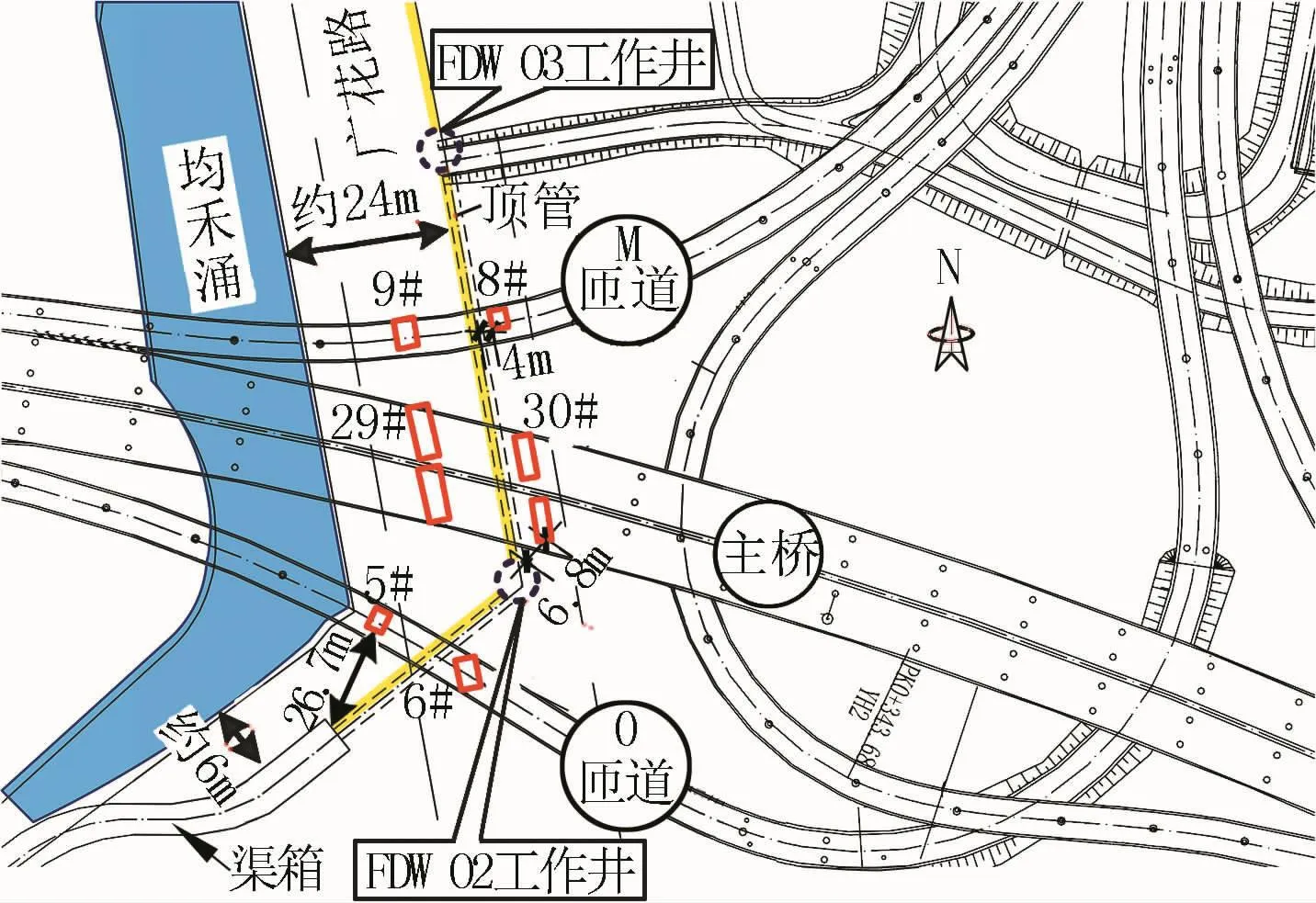
图3 顶管与高架桥桩的位置关系Fig.3 The diagram of the position relation between the pipe jacking and the viaduct pile

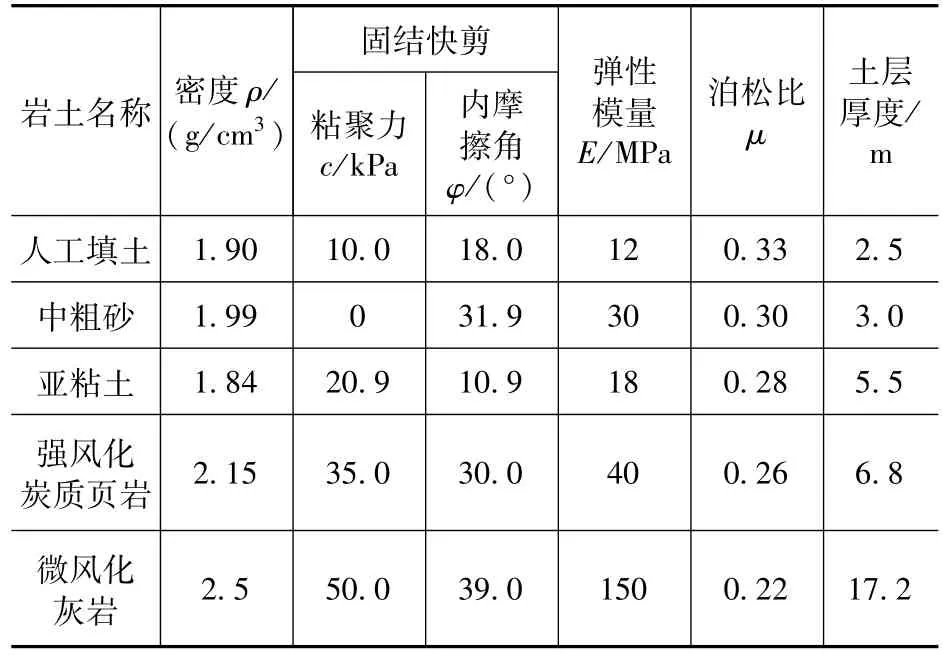
表1 土层物理力学参数Tab.1 Physico-mechanical parameters of soil

表2 管壁与土的平均摩阻力（单位：kN／m2）Tab.2 Average frictional resistance of pipe wall and soil（unit：kN／m2）

2.2 顶管力学参数计算

［10］计算顶管的迎面阻力：

式中：PF为顶管机的迎面阻力；Dg为顶管机外径，取3056mm；γs为上覆土的加权平均重度；Hs为地表面至顶管隧道中心的距离，取11.03m。将表 1及各参数带入公式（3）可得 PF＝1538.8kN。

顶管施工采用同步注浆，压力应小于0.4MPa～0.6MPa［11］，且横断面的注浆压力可近似认为随深度线性变化［12］，故此处计算取注浆压力作用分布形式如图4所示，其中 P1＝0.2MPa，P2＝0.35MPa，中间呈线性分布。

图4 隧道注浆压力作用分布Fig.4 Distribution of grouting pressure acting on tunnell

2.3 计算模型的建立

计算区域选取充分考虑隧道施工引起的沉降槽宽度，隧道施工的沉降槽宽度约为15m～20m［13］，故取计算模型几何尺寸X、Y、Z分别为102m、40m、35m。有限元分析时，在管片单元与实体单元之间加30mm厚的低模量单元来模拟注浆层，并假定其在衬砌周围等厚度分布，桥桩和承台根据原有设计，为C30强度等级混凝土材料。

模型的边界条件选取：土体上表面为透水自由表面，允许自由沉降，且孔压为零；左右两侧边界则约束水平向位移；土体底部则约束竖向土体位移。

计算中土体采用Mohr-Coulomb模型，基本力学参数由地勘报告和设计资料提供；注浆层厚度统一设置为30mm，采用弹性模型，在施工阶段弹性模量E＝200kPa，泊松比μ＝0.45，在施工完成后其弹性模量 E＝25MPa，泊松比 μ＝0.35；钢管则采用理想弹塑性模型，弹性模量E＝210GPa，泊松比μ＝0.3，屈服应力fy＝235MPa。桥桩及承台采用线弹性材料，根据弹性模量与泊松比计算材料体积模量和剪切模量。图5为总体计算模型有限元网格划分。

图5 计算模型有限元网格Fig.5 Finite elementmeshes ofmodel

根据实际施工步骤，定义计算工况如表3所示，其中，工况1进行初始地应力场计算，由于历史上土层在自重应力的作用下已经稳定，且桥梁施工产生的位移亦已稳定，将工况1与工况2进行位移清零，仅分析后续顶管工作井开挖及掘进施工引起的增量位移。

表3 模型计算工况Tab.3 Calculation conditions for themodel

3 计算结果与分析

3.1 桥梁桩基水平位移分析

在顶管近距离侧穿桥桩施工时，顶管工作井的开挖及掘进的过程对既有高架桥桩产生了一定程度的影响，而这种影响随着顶管的掘进而不断变化。

图6为顶管掘进81m与管道通水后的桥桩水平位移云图，由图可知FDW02工作井至FDW03工作井段管道的顶进施工主要对邻近高架桥主桥29＃、30＃桥墩和 M匝道8＃、9＃桥墩的桩基产生较大的位移，并以水平变形为主。其中由于主桥30＃桥墩桩基距顶管水平净距最小，故对其产生的影响最大，引起最大水平位移约为2.42mm，处于容许范围之内。

图6 桥梁桩基水平位移云图（单位：m）Fig.6 Horizontal displacement cloud picture of pile（unit：m）

图7为30＃桥墩侧向位移实测值与计算值的对比图，两种结果总体分布规律相同，实测最大值为2.65mm，与计算值相当，其他数值也较为吻合。

图7 桥桩侧移实测值与计算值对比Fig.7 Calculated and measured lateral value of pile

3.2 顶管与桥桩的相互作用

FDW02工作井至FDW03工作井段管道的顶进施工对邻近高架桥主桥桥墩的桩基产生较大的位移，使得桩周土体的应力发生了释放及重分布。文章根据数值计算出的桥桩水平位移数据，利用曲线拟合中的线性最小二乘法，选取最不利工况，反算桥桩的弯矩，借此评价桥桩的受力状态。

对于桥桩而言，桩长远大于桥桩结构水平位移，f（x）／x与1相比可以忽略，因此，变形曲线和变形曲率之间的关系及与杆件所受弯矩M之间的关系可以用如下公式表示：

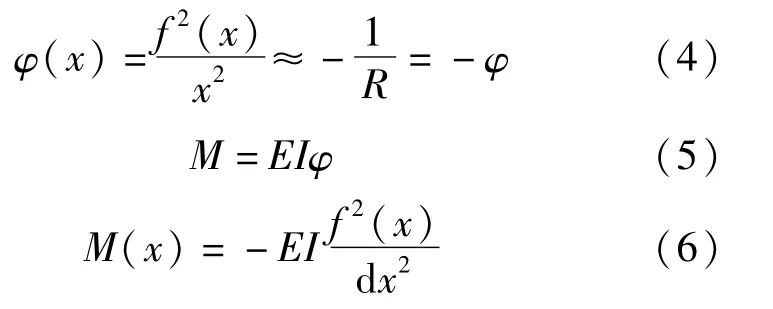
式中：x为桥桩沿着深度方向的坐标数据；R为函数图形的曲率半径；φ为函数曲率；EI为杆件截面抗弯刚度；M是要求的截面弯矩。

将已知数据代入公式（4）～公式（6）得到29＃桥墩桩基与30＃桥墩桩基最大弯矩增量图，如图8所示，图中标记数值代表单元内力，前者为大值，后者为小值。

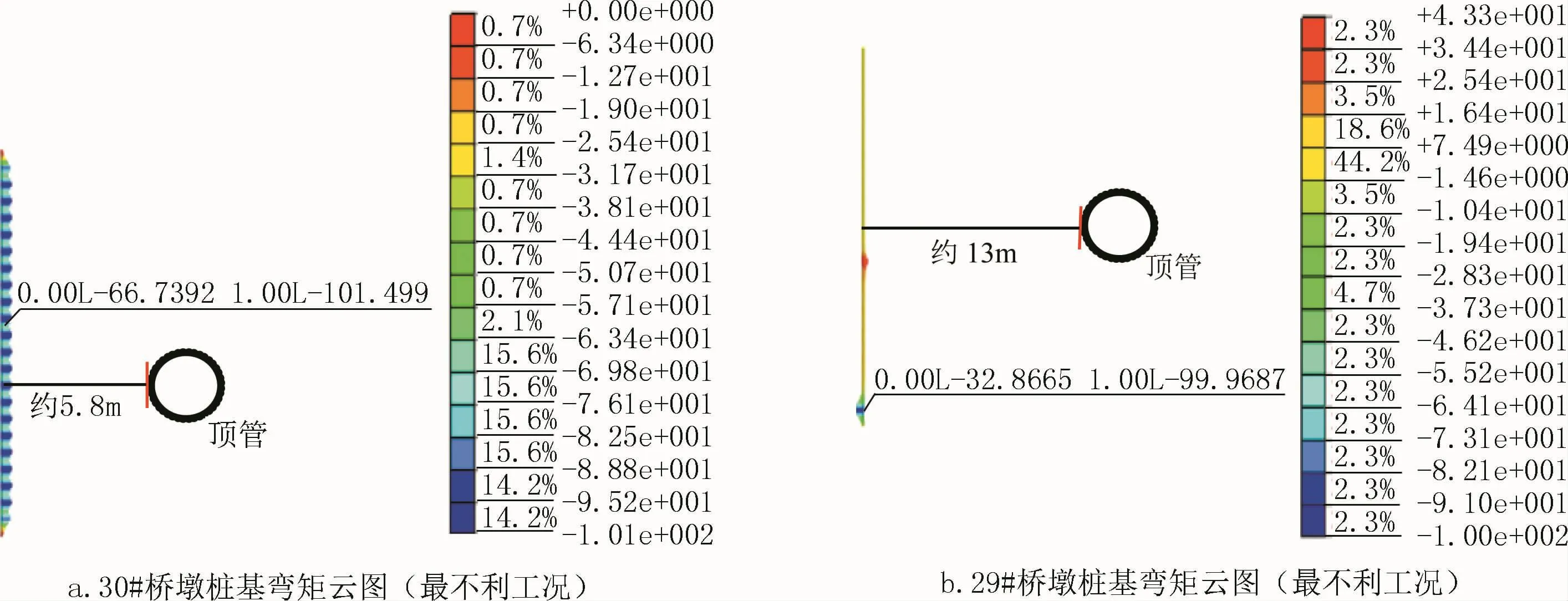
图8 桥桩弯矩增量图（单位：kN·m）Fig.8 The curve of the pile bendingmoment（unit：kN·m）

由图8显示，30＃桩基弯矩大于29＃桩基弯矩，这说明在应力重分布中，土体应力随着桥桩距顶管轴线的距离变化而变化，即距顶管轴线越近其应力越大。桩基的不同位置受到的土的水平应力不同，所以会产生应力差，如果应力差足够大，使得桩基产生剪切破坏，离顶管轴线位置越近，桩基相邻位置的应力差则越大，在本例中，应力差最大为0.15MPa。

3.3 地表沉降分析

顶管掘进施工会破坏原有地层的初始应力状态，诱发地表沉降，这将对邻近桥桩基础造成不利影响。为具体了解顶管施工对地层的影响，取顶管施工至45m处（前后3D范围内，其中D表示顶管直径，即3000mm；“＋”表示顶管工具头前方，“－”表示顶管工具头后方）正上方土层地表沉降的变化情况，具体见图9。

图9表明，在顶管施工过程中，顶管机头前方隆起明显，机头通过后，地表出现一定程度的沉降，这一点主要是受到正向推进力的挤压作用。地面沉降呈以顶管轴线为对称轴且开口向上的抛物线拱形，与Peck沉降槽规律相近，横向由顶管轴线向两侧递减，主要受影响区域为－10m～10m，即（－3.2D～3.2D）。

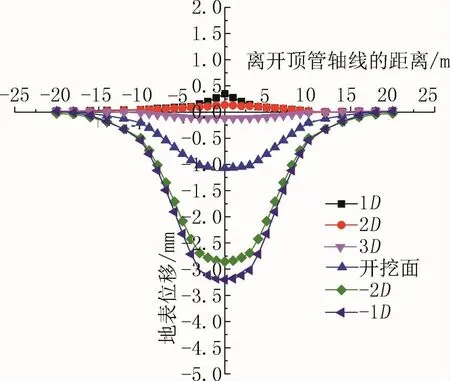
图9 地表沉降变化曲线Fig.9 Curves of ground settlement surfaces

根据工程实际情况，假设地层损失率为1.5%，提取地表位移理论计算结果与数值计算结果进行对比，如图10所示。

图10 地表位移理论计算值与数值计算结果对比Fig.10 Comparison of calculated value of settlement

图10显示，数值计算结果总体规律与理论计算结果趋于一致，地表最大沉降出现在顶管轴线正上方位置，理论值约为3.03mm，较数值计算结果小约5.6%，说明该计算模型简化和参数取值是可行的，理论值与计算值出现偏差是因为理论值中仅考虑了地层损失的影响，而数值计算值则是正面顶推力、地层损失及侧向摩阻力综合作用的结果。

4 结语

基于MIDAS-GTS软件建立顶管工作井开挖及顶管掘进过程的三维数值模型，计算了顶管侧穿高架桥桩产生的变形与应力，结果表明：

1.桥桩产生较大的变形，主要以水平位移为主，最大位移出现在30＃桥墩处，约2.42mm，且随着距离顶管轴线的距离增大而减小。

2.桥桩应力随着桩距顶管轴线的距离变化而变化，距离顶管轴线越近其应力越大。

3.数值计算得到地表沉降最大值为3.2mm，与Peck计算结果接近，横向主要受影响区域为－10m～10m，即（－3.2D～3.2D）。

本文建立的顶管施工计算模型能较好地反映隧道各施工阶段的力学性态，数值计算结果与理论值及实测值接近，可用于预测后续顶管隧道施工引起临近桩体侧移、桩体受力和地表沉降结果。

参考文献

［1］洪开荣.我国隧道及地下工程发展现状与展望［J］.隧道建设，2015，35（2）：95－107 Hong Kairong.State-of-art and Prospect of Tunnels and Underground Works in China［J］.Tunnel Construction，2015，35（2）：95－107

［2］葛春辉.顶管工程设计与施工［M］.北京：中国建筑工业出版社，2011

［3］张云军，宰金珉，王旭东，等.隧道开挖对临近桩基影响的二维数值分析［J］.地下空间与工程学报，2005，1（6）：832－837 Zhang Yunjun，Zai Jinmin，Wang Xudong，et al.Two-dimension Numerical Analysis of the Influence of Pile Foundation Induced by Adjacent Tunnel Excavation［J］.Chinese Journal of Underground Space and Engineering，2005，1（6）：832－837

［4］张恒，陈寿根，邓稀肥.盾构法施工对地表及桥梁桩基的影响分析［J］.地下空间与工程学报，2011，7（3）：552－557 Zhang Heng，Chen Shougen，Deng Xifei.Analysis on Influence of Shield Tunneling on Ground and Bridge Pile［J］.Chinese Journal of Underground Space and Engineering，2011，7（3）：552－557

［5］沈建文，刘力.盾构隧道施工对临近桥桩影响数值及现场监测研究［J］.岩土力学，2015，36（增2）：709－714 Shen Jianwen，Liuli.Numerical Analysis and Field Monitoring for Studying Effects of Shield Tunnell-ing on Nearby Piles［J］.Rock and Soil Mechanics，2015，36（S2）：709－714

［6］冯海宁，龚晓南，徐日庆.顶管施工环境影响的有限元计算分析［J］.岩石力学与工程学报，2004，23（7）：1159－1162 Feng Haining，Gong Xiaonan，Xu Riqing.Finite Element Analysis of Influence of Pipe-jacking Construction on Environments［J］.Chinese Journal of Rock Mechanics and Engineering，2004，23（7）：1159－1162

［7］李早，黄茂松.隧道开挖对群桩竖向位移和内力影响分析［J］.岩土工程学报，2007，29（3）：771－777 Li Zao，Huang Maosong.Analysis of Settlement and Internal Forces of Group Pile Due to Tunneling［J］.Chinese Journal of Geo-technical Engineering，2007，29（3）：771－777

［8］毛海和，俞兆磊.采用顶管掘进施工对杭州地层影响的探讨［J］.施工技术，2005，34（6）：27－30 Mao Haihe，Yu Zhaolei.Discussion About Influence of Pipe Jacking Tunneling Construction on Strata in Hangzhou Area［J］.Construction Technology，2005，34（6）：27－30

［9］房营光，莫海鸿，张传英.顶管施工扰动区土体变形的理论与实测［J］.岩石力学与工程学报，2003，22（4）：601－605 Fang Yingguang，Mo Haihong，Zhang Chuanying.Theoretic and Testing Analysis of Soil Deformation in the Area of Disturbance Caused by Pipe-jacking［J］.Chinese Journal of Rock Mechanics and Engineering，2003，22（4）：601－605

［10］葛春辉.顶管工程设计与施工［M］.北京：中国建筑工业出版社，2011：1－276

［11］方勇，何川.考虑施工过程的土压平衡式盾构隧道掘进数值分析［J］.铁道工程学报，2009（11）：56－60 Fang Yong，He Chuan.Numerical Analysis of Earth-pressurebalance Shield Driving Considering Based on Construction Course［J］.Journal of Rail Way Engineering Society，2009（11）：56－60

［12］莫海鸿，杨春山，陈俊生，等.盾构隧道先隧后井施工中工作井支护结构优化［J］.中南大学学报（自然科学版），2016，47（4）：1346－1352 Mo Haihong，Yang Chunshan，Chen Junsheng，et al.Supporting Optimization ofWorkingWell in Shield Construction with Tunnel Followed by Well Excavation［J］.Journal of Central South University（Science and Technology），2016，47（4）：1346－1352

［13］杨春山，莫海鸿，陈俊生，等.近距离下穿盾构隧道对上覆运营地铁隧道的影响研究［J］.现代隧道技术，2015，52（5）：145－151 Yang Chunshan，Mo Haihong，Chen Junsheng et al.Influence of the Approaching Construction of Underlying Shield Tunnels on Overlying Metro Tunnels［J］.Modern Tunnelling Technology，2015，52（5）：145－151