基于Wolfe线搜索的修正共轭梯度算法

林穗华

(广西民族师范学院 数学与计算机科学学院， 广西 崇左 532200)

共轭梯度法是1952年由Hestence等[1]作为求解线性方程组的方法而提出，1964年Fletcher等[2]将其推广用于求解无约束非线性函数极小值.因具算法存储量小、收敛速度较快等优点，现已成为解决经济、工程应用等领域大型线性方程组和大型无约束非线性优化问题的有效方法之一.设目标函数f:n→连续可微，求解min{f(x)|x∈n}的共轭梯度法迭代格式为

xk+1=xk+αkdk,

(1)

(2)

其中:xk为第k个迭代点，dk为搜索方向，αk为步长因子，gk=f(xk)，βk为共轭参数.不同的共轭参数对应不同的共轭梯度法.著名的HS(Hestence-Stiefel)、DY(Dai-Yuan)共轭参数公式如下

其中:yk-1=gk-gk-1，‖·‖为欧氏范数.

HS方法数值性能较好，但一般非凸目标函数即使采用精确线搜索HS方法也不一定收敛[3]，DY方法收敛性好但数值表现一般. 为挖掘收敛性质和数值表现好的算法，类似PRP+(Polak-Ribiere-Polyak)方法和HS+方法的思想[3]，文[4-8]从不同角度对经典的参数公式进行非负性修改，如

MHS(modified HS)方法和VMHS(variant MHS)方法均在强Wolfe线搜索条件下收敛且数值表现良好；MDY(modified DY)方法只需弱Wolfe线搜索条件就能收敛；WC(Wang-Chen)方法不依赖线搜索条件满足充分下降性，且在假设条件αk≥α*>0下收敛.论文结合上述方法的优点，考虑新的修正方向调控参数，分析算法在弱Wolfe线搜索条件下的收敛性，并用数值实验检验其有效性.

1 参数与算法

受文[4-9]启发，考虑修正共轭参数如下

(3)

其中调比因子

(4)

基于参数βk，采用弱Wolfe-Powell线搜索WWP(weak Wolfe-Powell)，求解无约束优化问题min{f(x)|x∈n}的修正共轭梯度算法如算法1.

算法1

步骤1给定初值x1∈n，δ∈(0,0.5)，σ∈(δ,1)，μ≥1，ε≥0，d1:=-g1，k:=1.若‖gk‖≤ε，停止.

步骤2计算步长αk满足WWP线搜索准则

(5)

(6)

步骤3由(1)式计算xk+1.若‖gk+1‖≤ε，停止.

步骤4由(3)、(4)式计算βk+1，由(2)式计算dk+1.

步骤5k:=k+1，转步骤2.

受文[10-13]的启发，考虑结合谱梯度法形式的搜索方向，建立求解min{f(x)|x∈n}的修正谱共轭梯度算法如算法2.

算法2

算法1中步骤4改为：由(3)、(4)式计算共轭参数βk+1，由下式计算搜索方向dk+1

dk+1=-θk+1gk+1+βk+1dk，

(7)

其中谱参数

(8)

2 全局收敛性

为证明算法1、2的全局收敛性，对目标函数作如下假设

(i) 设水平集Ω={x∈n|f(x)≤f(x1)}有界, 其中x1为初始点.

(ii)f(x)在Ω上连续可微且导数满足Lipschitz条件，即存在常数L>0，使得

‖g(x)-g(y)‖≤L‖x-y‖，∀x,y∈Ω.

论文以下算法的收敛性分析中均假设‖gk‖≠0，否则目标函数的稳定点已获得，算法自动终止.

引理1算法1产生的搜索方向序列{dk}满足下降性：∀k≥1，有

(9)

证明由Cauchy-Schwarz 不等式可知

(10)

当k=1时,

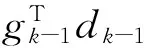
(11)

结合(3)、(4)式可得βk≥0.

(12)

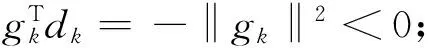
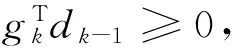
(13)

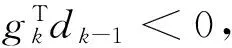
结合(10)～(12)式可得

(14)

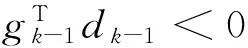
综上，由数学归纳法，引理1得证.由引理1的证明过程可得引理2.

引理2设{βk}为算法1产生的共轭参数序列，则∀k>1，有

(15)

由引理1及文[3]引理1.4.1,可得引理3.

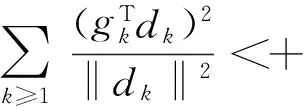
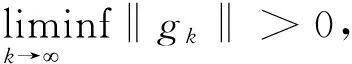
‖gk‖≥r, ∀k≥1.

(16)

由(2)式可得dk+gk=βkdk-1，两边取模平方，并移项可得

(17)

由(17)式递推，并结合(16)式可得

从而可得

这与引理3矛盾，由反证法知定理1得证.

引理4设{dk,βk}为算法2产生的序列,则∀k≥1，有

(18)

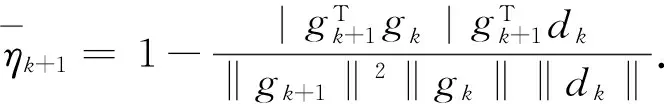
则

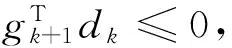
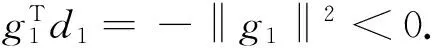
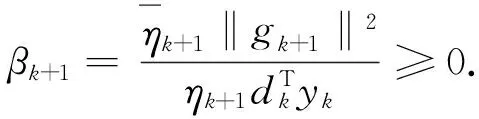
(19)

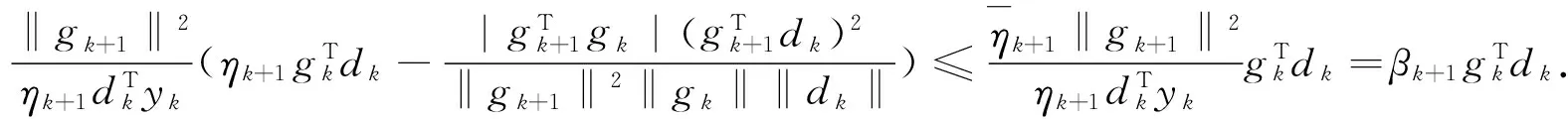
(20)

由归纳法知,∀

引理4说明算法2产生的搜索方向dk满足下降性.根据文[3]引理1.4.1,易得引理5.

证明由(7)式可得dk+θkgk=βkdk-1，两边取模平方，并移项可得

类似定理1，用反证法可得定理2结论.

3 数值实验

为测试论文提出的修正HS共轭梯度算法的有效性,用文[14]的测试函数进行数值实验，结果如表1所示.其中NI(number of iterations)表示算法迭代次数,time表示CPU时间(单位：s),目标函数为ROSE(Rosenbrock)、FROTH(Freudenstein and Roth)、BADSCP(Powell badly scaled)、JENSAM(Jennrich and Sampson)、HELIX(helical valley)、GULF(Gulf research and development)、SING(Powell singular)、WOOD、KOWOSB(Kowalik and Osborne)、BIGGS(biggs EXP6)、OSB2(Osborne 2)、ROSEX(extended Rosenbrock)、SINGX(extended Powell singular)、PEN1(penalty I)、PEN2(penalty II)、VARDIM(variably dimensioned)、TRIG(trigonometric)、BV(discrete boundary value)、IE(discrete integral equation)、TRID(Broyden tridiagonal)、BAND(Broyden banded)、LIN(linear-full rank) 、LIN1(linear-rank 1)、LIN0(linear-rank 1 with zero cols. & rows). 算法运行环境为Windows7+Matlab2011b. 算法Wolfe线搜索参数为δ=0.1，σ=0.9，终止条件为‖gk‖≤10-6，或迭代次数超过9 999.图1为迭代次数比较.图2为CPU时间比较.

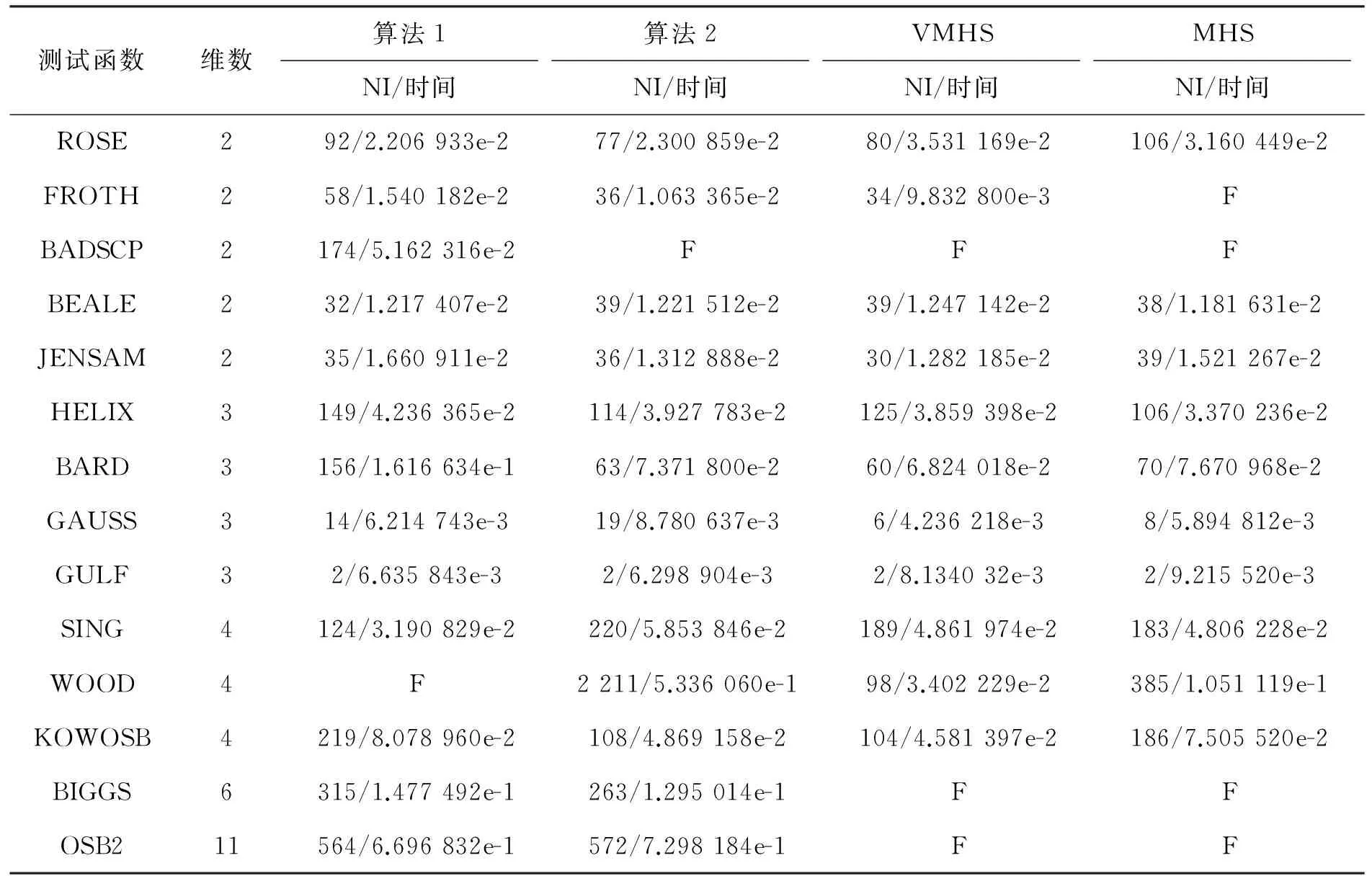
表1 数值实验结果

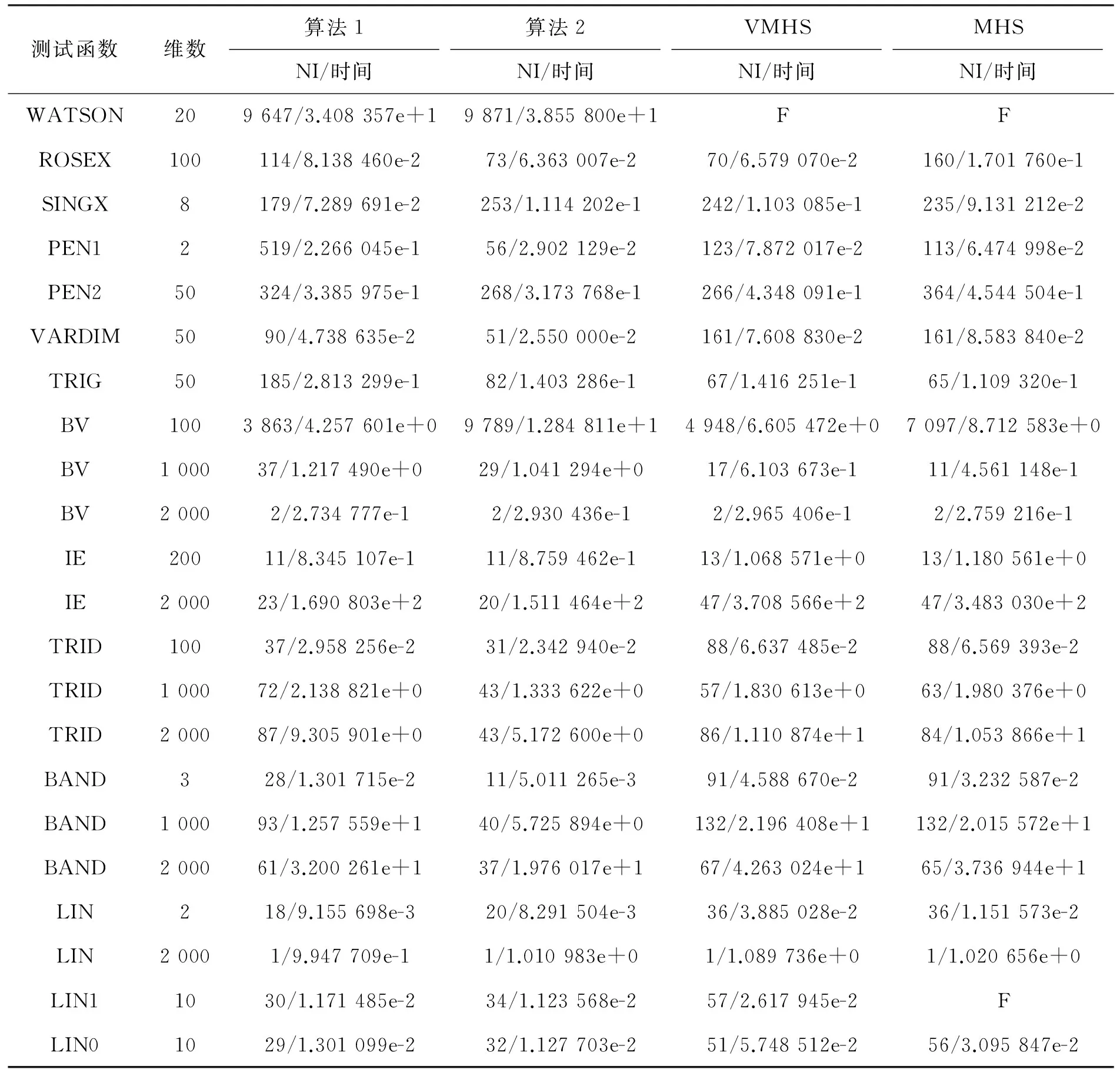
续表1

图1 迭代次数比较 图2 CPU时间比较

参考文献：

[1] HESTENES M R, STIEFEL E L. Methods of conjugate gradients for solving linear systems[J]. J Res Nat Bur Standards, 1952, 49 (6): 409-436.

[2] FLETCHER R, REEVES C. Function minimization by conjugate gradients[J]. Comput J, 1964, 7 (2): 149-154.

[3] 戴彧虹, 袁亚湘. 非线性共轭梯度法[M]. 上海: 上海科学技术出版社, 2001: 30-51.

[4] YAO S W, WEI Z X, HUANG H. A note about WYL’s conjugate gradient method and its application[J]. Appl Math Comput, 2007, 183 (1): 1341-1350.

[5] DU X W, ZHANG P, MA W Y. Some modified conjugate gradient methods for unconstrained optimization[J]. J Comput Appl Math, 2016, 305: 92-114.

[6] 黄海. 非线性无约束优化问题的新共轭梯度法[J]. 河南大学学报 (自然科学版), 2014, 44 (2): 141-145.

[7] 王安平, 陈忠. Wolfe线搜索下一种修正的HS共轭梯度法及其全局收敛性[J]. 安徽大学学报 (自然科学版), 2015, 39 (4): 16-19.

[8] 李灿. 一种修正PRP共轭梯度法的全局收敛性[J]. 安徽大学学报 (自然科学版), 2013, 37 (2): 41-44.

[9] JIANG X Z, JIAN J B. Two modified nonlinear conjugate gradient methods with disturbance fators for unconstrained optimization[J]. Nonlinear Dyn, 2014, 77 (1/2): 387-394.

[10] 赛·闹尔再, 吴晓云. 谱Hestenes-Stiefel共轭梯度算法及其收敛性[J]. 数学的实践与认识, 2015, 45 (18): 261-270.

[11] 林穗华, 黄海. 一个新的谱共轭梯度法[J]. 工程数学学报, 2014, 31 (6): 837-846.

[12] 林穗华. Wolfe线搜索下的修正FR谱共轭梯度法[J]. 山东大学学报 (理学版), 2017, 52 (4): 6-12.

[13] ZHANG Y, DAN B. An efficient adaptive scaling parameter for the spectral conjugate gradient method[J]. Optim Lett, 2016, 10: 119-136.