混合迭代学习法在发动机怠速稳速控制中的应用

崔建平，李登科，刘成基

(中国矿业大学(北京) 机电与信息工程学院，北京 100083)

0 引言

汽车发动机是工作在高温高压和变载荷环境下的复杂热-机系统(Thermomechanical System),是显著动态非线性、滞后性、多变量时变系统，因此很难建立其准确的数学模型，控制系统的设计也非常复杂。怠速工况是指发动机不对外做功，只是克服发动机内部的摩擦阻力，发动机输出功率为零，保持怠速转速稳定[1]，是发动机重要工况之一，也是汽车控制系统中最基本且重要的问题之一。

目前城市道路上汽车密集度越来越大，汽车在行驶时，约有30%的燃油在怠速工况中消耗了，因此有必要对怠速状态稳速控制进行研究,来减少怠速波动和燃油消耗。怠速控制的主要目的是在怠速有外部扰动，如冷却水温度的波动, 空调开关等和发动机具有参数不确定性时保持发动机转速的稳定[2]。良好的怠速控制，除了检测负载改变引起的扰动，同时需要能够兼顾发动机寿命、摩擦、不同的燃油形式、多变的驱动形式，甚至天气变化对怠速稳定的影响。因此，发动机怠速控制需要满足燃油经济性，降低排放，保证燃烧稳定，尽可能低的噪声、振动、不平顺性。

在处理非线性动态系统时，目前常用的方法是工作点分割成不同的操作点，在各操作点附近线性化处理。然后使用传统的线性控制模型，诸如比例积分微分控制(PID)、H∞优化控制等。尽管经典控制，现代控制到人工智能控制技术均已应用于汽车发动机怠速控制[2-4]，部分已取得良好的效果，在不精确的参数下可以获得可接受的性能表现，缺点是实际输出值不能准确快速地跟踪期望值，在很大程度上丢失发动机的性能，在燃油消耗、燃烧稳定性和排放限制的平衡上，仍然存在许多问题。因此，在发动机控制领域内需要设计更加先进的控制方法，来获得怠速控制的最佳性能。

迭代学习控制(Iterative Learning Control，ILC)是智能控制的一个分支，是一种新型学习控制策略。依靠系统实际输出与期望输出之间的偏差值不断优化控制信号，来调节输入输出值，经过若干次迭代后，系统的输出逐渐接近直至完全跟踪期望轨迹[5]。迭代学习控制的优点是：基于不需精确模型控制机制；收敛速度快；收敛性好；适应能力强；易于理解和实践应用[6]。

本文应用一种在传统PID控制策略下，结合比例积分的混合迭代学习控制法，将该方法应用于发动机状态变量模型的怠速稳速控制，在Simulink建立模型并分析，对比传统PID和混合迭代学习法的控制效果，验证该方法在汽车怠速稳速控制中的有效性和寻找自动调节发动机怠速的合适方法。结果表明：使用混合迭代控制器有更快的收敛速度，更小的绝对偏差，跟踪期望输出用时少，保持怠速转速快速稳定在期望值，性能表现远优于传统的PID控制器。

1 怠速稳速控制及控制原理

1.1 怠速稳速控制

发动机怠速情况下。混合气燃烧所作的功只是用来克服发动机内部的摩擦阻力，使得发动机保持目标转速稳定运转[7]。因此怠速控制的目标是在尽可能降低排放的前提下在尽可能短的时间内将转速稳定在目标转速附近。

当发动机处于怠速工况时，若当前转速脱离目标转速，发动机ECU发出控制指令，调节混合器进气量或点火提前角，最终使发动机转速稳定在目标转速附近。一般车用柴油机怠速转速在500～800 r/min，汽油机怠速转速在700～1 000 r/min。

1.2 PID控制基本原理

比例积分微分(PID)控制器是基于负反馈原理，其优点在于不需要确切了解被控对象的数学模型，只需根据经验调整调节器参数即可取得良好的控制效果，结构简单，鲁棒性强，是目前控制系统应用最广泛的一类控制器。模拟PID控制表达式可得：

(1)

式中:r(t)为给定信号，y(t)为输出信号，e(t)为偏差信号，e(t)=r(t)-y(t)；kp为比例常数；ki为积分常数；kd为微分常数。传统PID控制发动机系统原理图如图1所示。

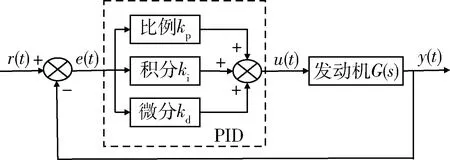
图1 传统PID控制发动机系统原理图

1.3 混合迭代学习控制方法

迭代学习控制是智能控制的一个重要分支，是在特定时间区间里，根据输出信号与目标信号的偏差不断修正的控制信号，通过修正下一次控制参数，不断提高系统的质量和跟踪性能[8]。

迭代学习控制不依赖于动态系统的精确数学模型，可以简单方便地处理复杂未知的动态系统，对设计者的经验知识和计算量要求较少，同时适应性强，易于实现[9]；对一些非线性、复杂性、难以建模以及高精度轨迹控制问题有很强的适应能力。

迭代学习控制可分为开环学习和闭环学习。在闭环迭代系统中，当前控制变量通过系统当前的输出偏差来获得。一般来说，系统偏差存在正负，为减少迭代计算量以及使迭代过程朝着同一方向收敛，这里系统偏差ek均指最大稳态偏差的绝对值。

迭代学习法中系统输出偏差为：

ek(t)=yd-yk(t)

(2)

闭环迭代系统当前控制变量uk+1(t)的通用公式为:

uk+1(t)=φ(uk(t),ek+1(t))

(3)

式中：yd(t)为输出变量期望值；yk(t)为系统实际输出变量。

传统PI控制与闭环迭代学习控制结合，称为混合迭代学习控制法。给定期望输出yd(t)和初始状态uk(0)，在给定时间t∈[0,T]内，混合迭代学习控制法控制变量uk(t)按照公式(4)进行多次重复运行。

(4)

式中：Tp和Ti分别是PI迭代学习增益。

在特定时间t∈[0,T]内，当前控制变量uk+1(t)包含上次值uk(t)和当前的输出偏差下的闭环迭代系统输出值。输出偏差ek+1(t)用来修正控制变量uk+1(t)。当迭代次数k增加时，使系统输出yk(t)→yd(t)。所得的偏差ek(t)经过迭代学习律得出下次的控制输入uk+1(t)并存入控制存储记忆单元，到下次控制时再调用。在每次迭代运算后，若满足停止条件ek(t)≤e0，则迭代计算停止。混合迭代学习控制原理图如图2所示。

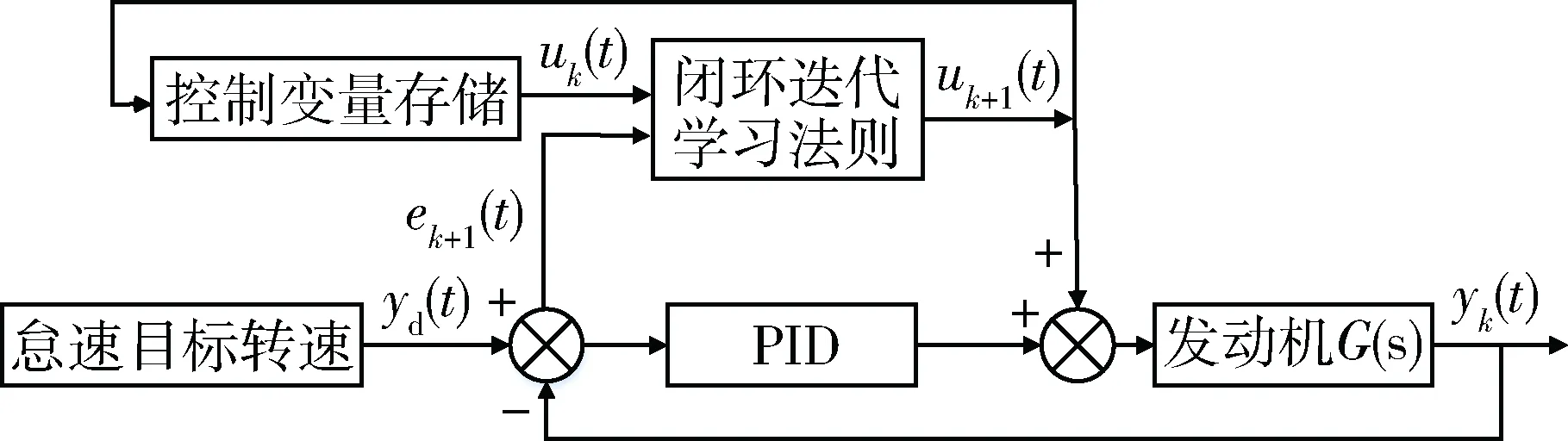
图2 混合迭代学习控制原理图

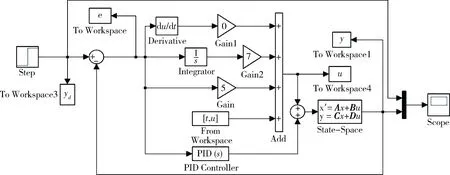
图4 发动机怠速的状态变量模型的仿真结构图

此外，其他类型的迭代学习，如高阶迭代学习控制算法、最优迭代学习控制算法、遗忘因子迭代学习控制算法和反馈-前馈迭代学习控制算法，以及与其他方法结合的算法，例如神经网络控制[10]、模糊控制[11]、自适应控制[12]等，均取得成功。

考虑到汽车发动机系统是个动态系统的连续非线性时变模型，状态和输出方程用式(5)表示。

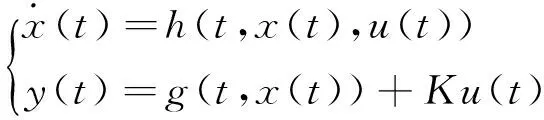
(5)

x∈Rn,u∈Rm,y∈Rv，x为系统状态矢量，u为系统控制矢量，y为系统输出矢量，K为迭代学习增益，系统在时间间隔t∈[0,T]重复运行。h，g为状态变量、输入变量和时间三者的非线性函数关系式，保持不变。

经过k次迭代后，系统输出状态为：

(6)

发动机怠速稳速控制运行的迭代学习算法过程如图3所示。

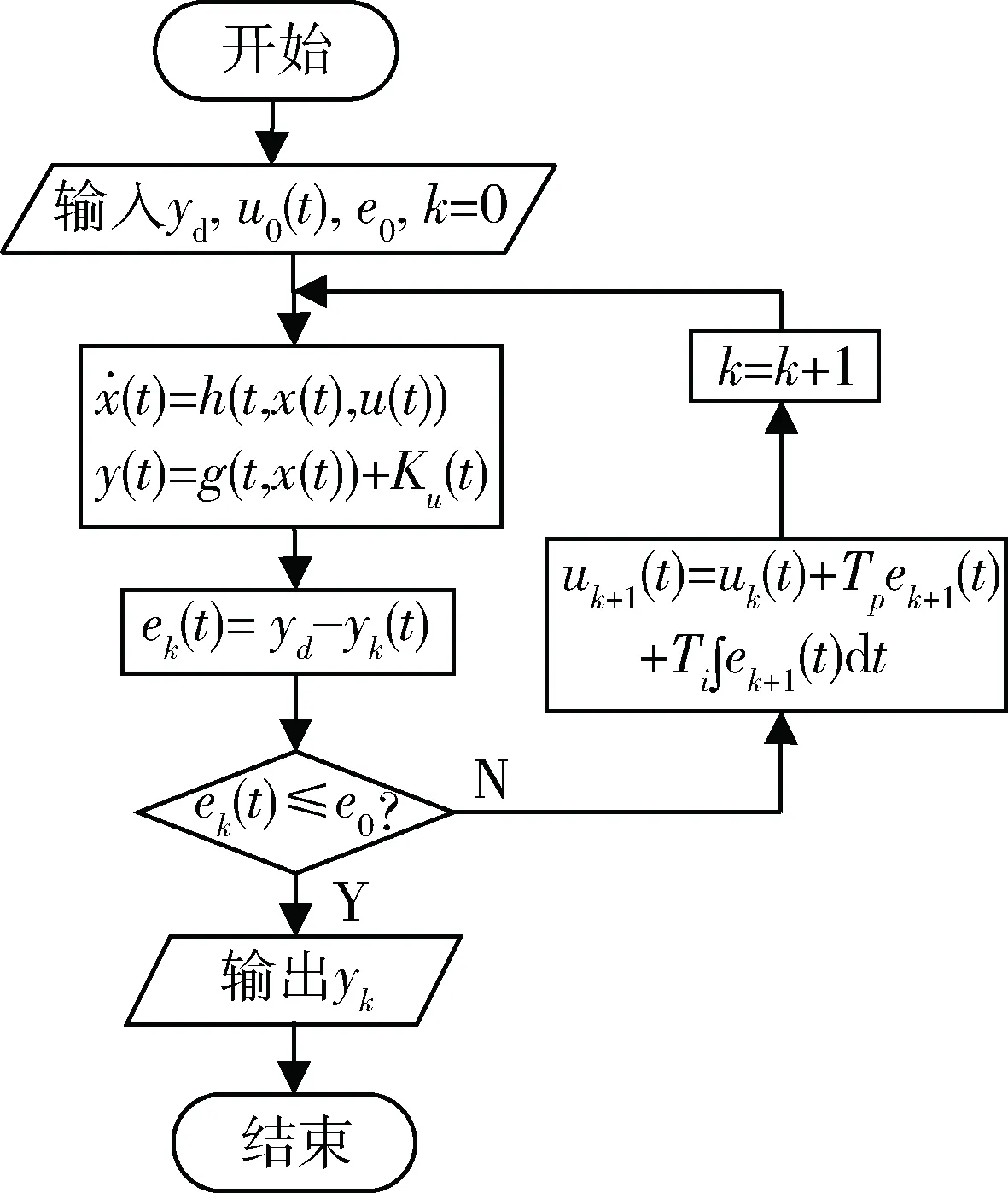
图3 发动机怠速迭代学习算法流程图

2 发动机状态变量模型及仿真分析

2.1 发动机状态变量模型

混合迭代学习控制具有能够不依赖明确的发动机控制模型、运行稳定、适应能力强、能够提高瞬时响应和跟踪效果的优点，广泛应用于不同控制目标的现代汽车发动机控制中。利用辨识的发动机稳态模型[13]，将混合迭代学习控制应用于发动机怠速稳速控制中，通过比较传统PID 和混合迭代学习的控制效果，以寻求在线校正发动机怠速转速最适宜的方法。

在仿真系统中，发动机怠速状态变量模型在稳定工作点为(x,y,u)，如式(7)所示：

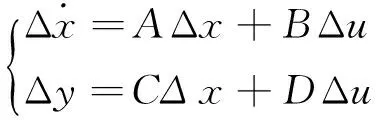
(7)

式中：x=[TW,NH]，为状态变量，分别代表冷却水温度和怠速转矩；u=[θa]，为控制变量，代表发动机混合燃料进气量；y=[V]，为输出变量，表示发动机实际转速。

模型构建基于基本物理学规律、理论推导结合辨识技术，建立影响发动机怠速的各个输入变量的关系及其对输出转速产生的影响，忽略物理磨擦等因素以及其他次要的损失，仅考虑发动机怠速转矩和冷却水温度。应用混合迭代学习法，发动机怠速期望转速为800 r/min。控制器PI学习增益kp=5,ki=7；发动机状态变量模型的矩阵系数为：

C=[-0.192 6 1.710 7],D=[0.001 3]

发动机怠速状态变量模型迭代学习控制Simulink仿真结构图如图4所示。

2.2 仿真分析

当发动机处于稳定怠速工况时，设冷却水温恒定，选取怠速目标值800 r/min，在负载基本恒定不突变和无外加干扰时观察控制系统的转速波动曲线，设定输出最大超调量小于10%，调节时间小于1.0 s。

使用阶跃响应分析方法，将转速分别从启动(转速为零)升速到稳定800 r/min(下文以0～800表示)以及从巡航速度1 500 r/min降到期望的怠速转速800 r/min(下文以1 500-800表示)。在Simulink中建立仿真模型，以观察传统PID和混合迭代学习两种控制器的输出响应，检验控制方法的合理性及控制器效果。

图5、6给出了将发动机转速从巡航速度1 500 r/min降到期望的怠速转速800 r/min时，两种控制器仿真输出和最大绝对偏差值曲线图。

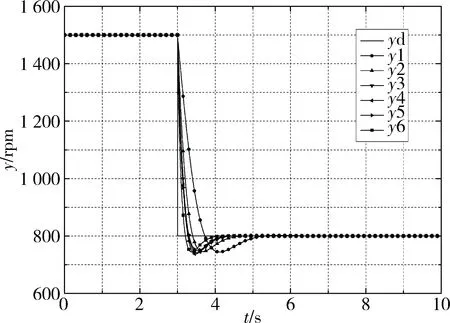
图5 状态变量模型的系统信号输出(1 500-800)

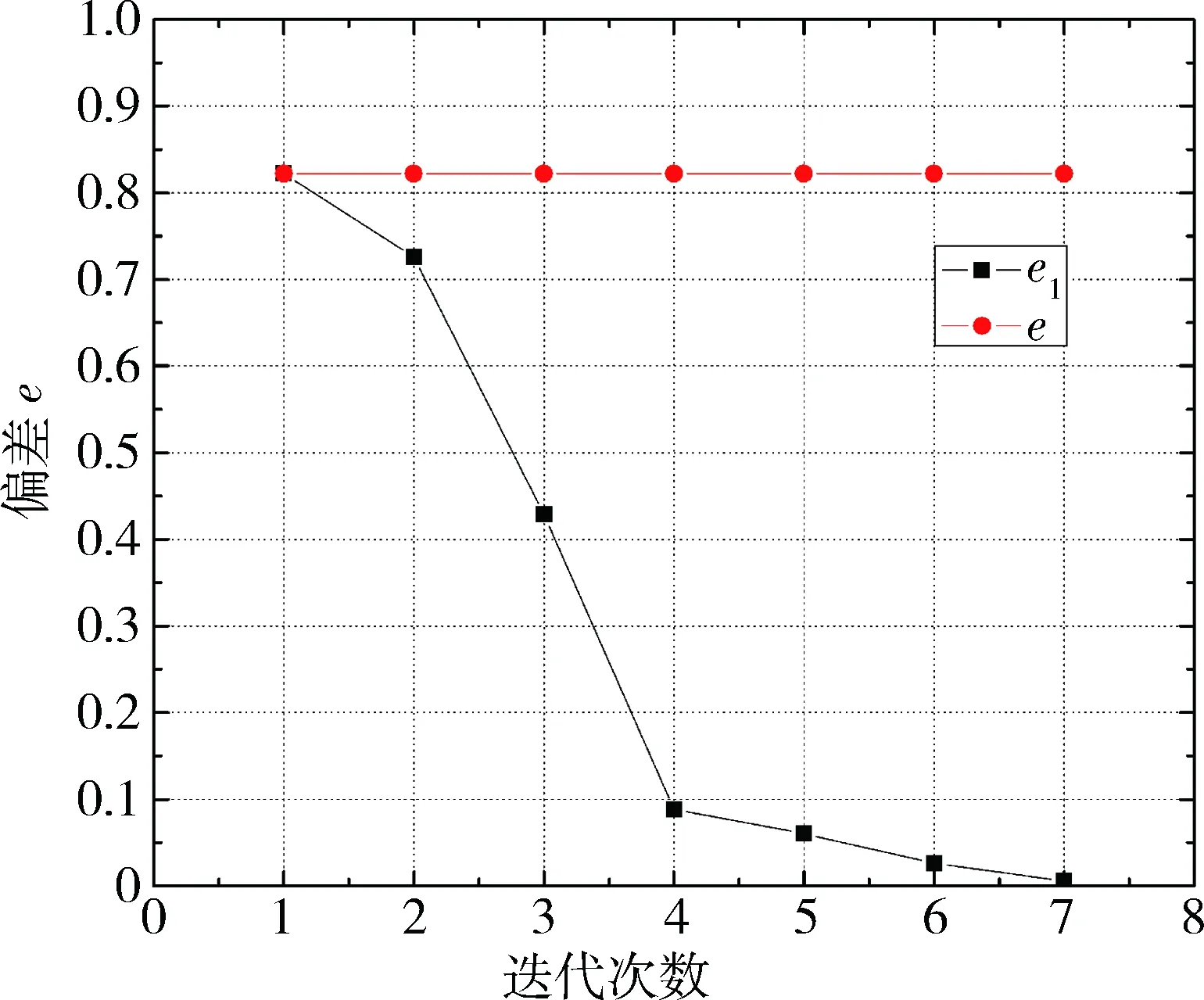
图6 状态变量模型系统输出偏差(1 500-800)

在图6中，e是传统PID控制系统最大绝对输出偏差，e1是混合迭代控制系统最大绝对输出偏差。随着迭代次数增加，混合迭代学习系统的最大绝对输出偏差迅速减少，第三次迭代开始，系统偏差接近零并稳定，系统实际输出很好地跟踪目标值。而传统PI控制系统的最大绝对误差基本不变。

在图5和6中，对比传统PID控制效果和混合迭代学习控制效果，可见混合迭代学习系统的收敛率很快，系统偏差迅速减小并趋于一个很小的稳定值。在迭代学习后，控制系统所有的执行指标均逐渐改善，跟随期望轨迹用时更少，怠速稳定性提高，有很好的控制效果。

图7、8给出了将发动机转速从启动(转速为零)升速到怠速稳定的800 r/min时，两种控制器仿真输出和最大绝对偏差值曲线图。

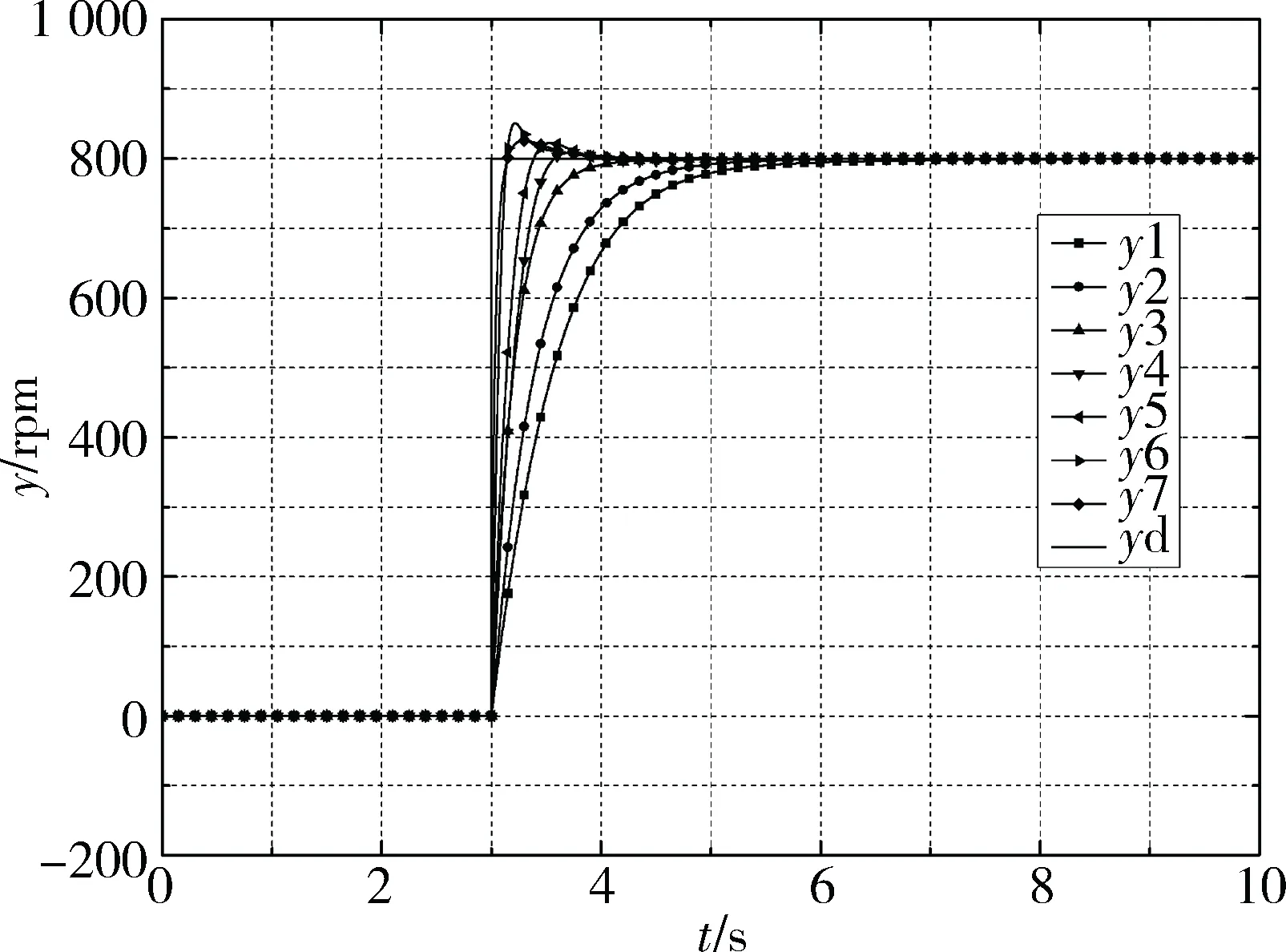
图7 状态变量模型的系统信号输出(0-800)

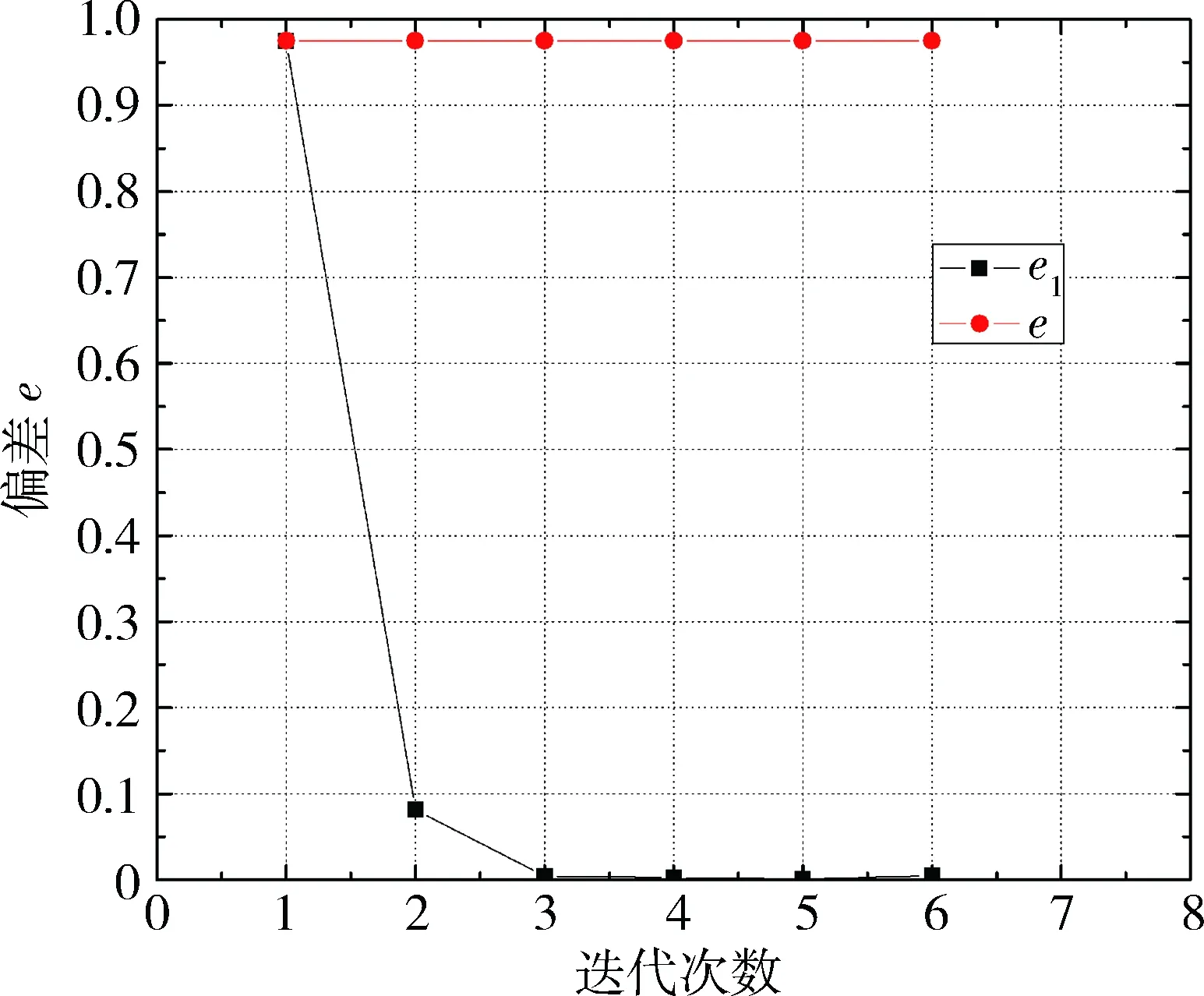
图8 状态变量模型系统输出偏差(0-800)

同样，在图7中，在特定时间t∈[0,10]s内，对于传统PI控制系统，系统运行后ts=4.28 s，在混合迭代学习系统中第一次迭代后ts=4.28 s，没有超调量7.31%；第二次迭代ts=3.69 s，超调量为7.38%；第三次迭代ts=2.12 s，超调量为9.34%；第四次迭代ts=1.67 s，超调量为10.02%。随着迭代次数的增加，调节时间逐渐变短，超调量逐渐增加，在第6次迭代结束时，已经得到良好的跟踪效果。

在图8中，e是传统PID控制系统最大绝对输出偏差，e1是混合迭代控制系统最大绝对输出偏差。随着迭代次数的增加，传统PI控制系统的最大绝对误差不变，输出信号与期望轨迹还有很大的差别。混合迭代学习系统的最大绝对输出偏差迅速减少，仅经过6次迭代，系统偏差接近零，系统实际输出很好地跟随期望信号。

同样，在图7和8中，对比传统PID控制效果和混合迭代学习控制效果，可以得出如前所述的控制效果。

3 结论

本文通过对汽车发动机怠速稳速控制的研究，将一种新型控制方法运用于发动机怠速状态变量模型中，实现在线自动跟踪目标转速。仿真实验结果表明，无负载干扰情况下，混合迭代学习控制器在发动机状态变量模型有更快的收敛速度，更小的绝对偏差和更好的控制效果。不仅缩短了发动机怠速的调节时间，且提高了发动机怠速系统的稳态性能。在进一步的研究中，可以充分考虑怠速控制的多目标、多闭环调节，在发动机不同的工作点，混合迭代学习控制器有更好的控制效果和跟踪精度，该方法的优势会得到更好的体现。

[1] 王帅. 汽油发动机怠速控制方法研究[D]. 哈尔滨：哈尔滨工业大学,2010.

[2] 刘春燕，钮王杰，闫池.基于Fuzzy-PID 汽油机怠速控制器的设计[J].重庆交通大学学报(自然科学版)，2011，30(2)：300-302.

[3] 何吕君,兰永红,黄辉先.基于观测器的发动机怠速控制[J]. 计算机工程与应用,2014, 50(20):259-263.

[4] 李文礼,石晓辉,柯坚, 等. 基于滑模迭代学习的发动机怠速扭振模拟技术[J]. 振动、测试与诊断,2016, 36(2):359-365,406.

[5] 林辉，王林．迭代学习控制理论[M]．西安：西北工业大学出版社，1998.

[6] 许慧敏. 非线性系统迭代学习控制算法研究[D].北京:华北电力大学,2016.

[7] 杨莹. 汽车发动机电控系统设计及怠速仿真研究[D].武汉:武汉理工大学,2012.

[8] 李玉忍,张林,郑宏民. 迭代学习在PID控制中的应用[J]. 计算机应用,2008,28(S1):5-6,9.

[9] 郝晓弘,李卓悦,王华. 非线性系统在任意初值下的PID型迭代学习控制[J]. 计算机科学,2016,43(2):283-286.

[10] AHN H S, Chen Yangquan, MOORE K L. Iterative learning control: brief survey and categorization[J]. IEEE Transactions on Systems, Man and Cybernetics, Part C (Applications and Reviews), 2007, 37(6): 1099-1121.

[11] 余琼霞,侯忠生. 非参数不确定系统的自适应迭代学习控制[J]. 系统科学与数学,2016, 36(1):1-13.

[12] 郝晓弘,金亚蓉,马宇,等. 基于遗传算法的模糊迭代学习控制算法[J]. 计算机应用,2013, 33(4):960-963.

[13] TENGKU N A, TUAN K, INTAN Z, et al. System identification for internal combustion engine model[C]//Asia International Conference on Modelling & Simulation, 2012: 17-22.