一道解析几何题的巧思妙解
2018-03-29李金莲
新课程(下) 2018年4期
李金莲
(甘肃省武威市古浪县第一中学,甘肃 武威)

【思考1】求△AOB的面积,一般需要计算底和高,分别为弦长和点O到直线AB的距离,于是有如下两种解法:
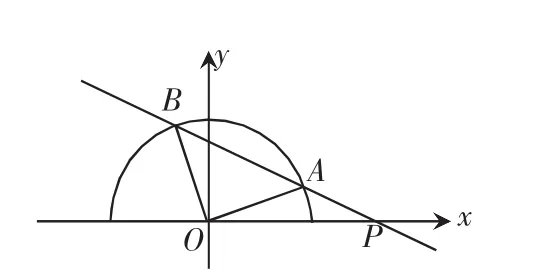
图1
由题意得 Δ=8k2-4(1+k2)(2k2-1)>0,所以 k2>1.
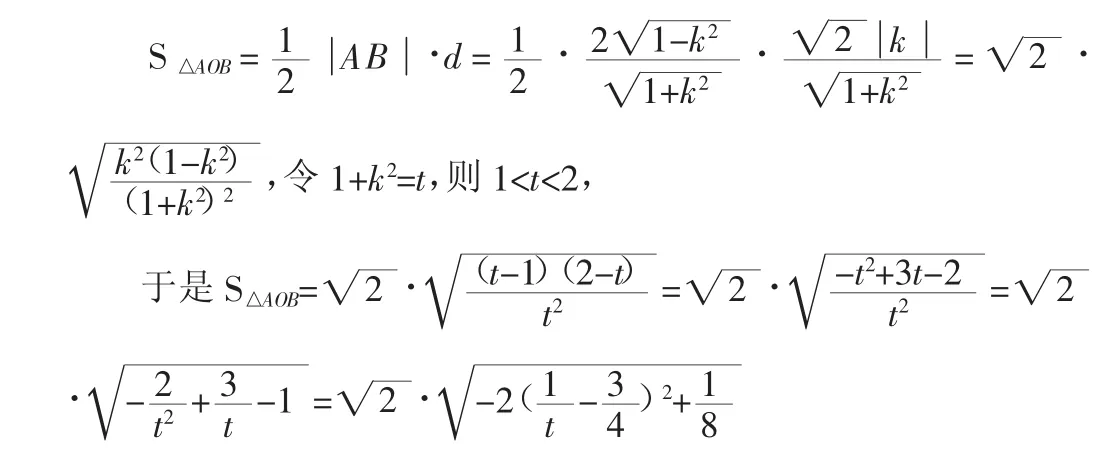
【思考2】坐标法是解决解析几何问题的常用方法,但是以上两种解法都比较繁琐,运算量很大,而在解决具体问题的过程中,利用几何性质往往可以简化运算,于是有如下两种解法:

图2
【思考3】这只是一道选择题,而选择题本身有很多特有的解法,如:特值法、排除法、验证法、筛选法等等,于是有如下解法:
【解法5】易知直线l的斜率为负值,故可排除A、C,若直线的斜率为可计算得S△AOB=1,若直线l的斜率为可计算得故选 B.
【点拨】高中数学旨在培养学生的逻辑思维能力,培养思维的灵活性、广阔性、发散性,若能从一道题入手,经过深入细致的分析和研究,便能找到巧妙的、简洁的方法.因此,我们一线教师在日常教学中应多思考、多钻研、多探究,在解决问题的过程中让学生的思维得到尽可能的开发、锻炼和培养.
