巧引平行线 妙求线段比——以三角形为背景的线段比值求解的“一招制敌”术

安徽省合肥市肥东县龙塘学校 章 林

对于以三角形为背景的线段比值问题的求解，“梅内劳斯（Menelaus）”定理可以说是一个“一招制敌”的绝技，但是在中学阶段，梅内劳斯定理既不属于课标和教学要求，初中生也不易掌握。除却梅内劳斯定理，还有一种“一招制敌”的绝技可以轻松解决以三角形为背景的线段比值问题，这种方法就是：巧引平行线，利用相似三角形或平行线分线段成比例定理，进而求比值。本文试以一道中考试题为例，详述在三角形背景下求线段的比值问题中，如何巧引平行线，妙求线段比值的“一招制敌”术，并在解题“竞技”中应用之。

一、基本结论

在三角形背景下，与线段比值有关的结论主要有以下两条：

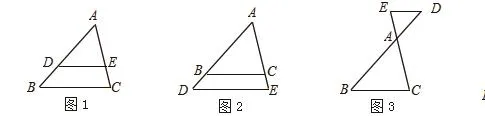
【结论1】平行于三角形一边的直线截其他两边（或延长线）所得的对应线段成比例。(证明略)即：如图1，图2，图3，在△ABC中，DE∥BC，分别交直线AB、AC于D、E，则有

作为特例，还有下面的结论：

【结论2】过三角形一边的中点，平行于另一边的直线，必平分第三边。几何语言可表示为：（如图1）若DE∥BC， D为AB中点，则E为AC的中点。

二、基本图形

在结论的三种情形中包含两类基本图形，不妨称为“A”字形（如图1）和“X”字形（如图2）。在这两个基本图形中，均有：

三、方法解析

在三角形背景下求线段的比值，往往需借助于相似三角形，而平行线是构造相似三角形的重要条件。一般来说，如果图中已有平行线或相似三角形，则只需找到图中的“A”字形和“X”字形图，若没有平行线也没有相似三角形，则可以通过添加平行线构造出相似三角形，再直接或间接地进行线段比值的求解。那么如何巧添平行线，构造相似三角形呢？下面以一道求线段比值的中考试题为例，详细剖析添加平行线的方法。

【引例】如图4，已知△ABC，延长BC到D，使CD=BC。取AB的中点F，连接FD交AC于点E。（1） 求AE∶AC的值；（2）若AB=a，FB=EC，求AC的长。

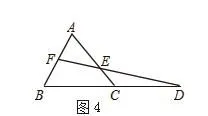
【解析】这里重点解析第（1）题。图中没有相似三角形，也没有平行线，要求AE∶AC的值，可以构造相似三角形进行直接求解或间接转换。我们看到图中有6个标出的点，分别是A、B、C、D、E、F。我们从其中的任一点出发，看看能否作出和已知线段（直线）平行的直线，从而构造出相似三角形。

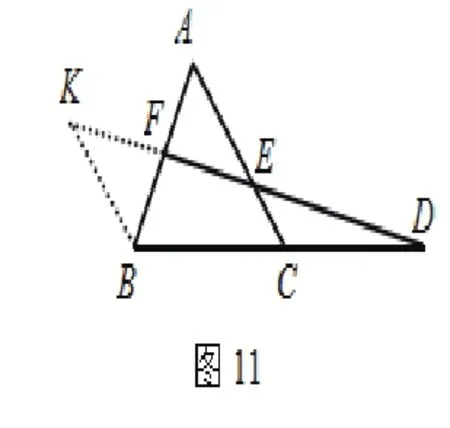
先从点A开始，我们发现经过点A可以作出FD的平行线（如图5），交BD的延长线于点K。在这个图形中蕴涵着以下两个“A”字形的基本图形，分别如图6和图7所示。

在图6中，由AK∥FD，F为AB的中点可得D是BK的中点，又由C是BD中点可得CD∶CK=1∶3， 结合图7可得CE∶CA=1∶3，所以AE∶AC=2∶3。

另一方面，经过点A还可以作出BC的平行线，并与DF的延长线交于点K（如图8）。在此图形背景中，隐藏着下面两个“X”字形图，分别如图9、10所示。

在图9中，由AK∥BD，F为AB的中点可得F是DK的中点，可得△AEK≌△BFD，所以BD=AK；又由C是BD中点可得CD∶AK=1∶2，结合图10可得CE∶CA=1∶3，所以AE∶AC=2∶3。这样，从点A出发可以引出两条平行线，相应地产生了相似三角形，再挖掘其中隐藏的“A”字形和“X”字形图，可以使问题轻松解决。

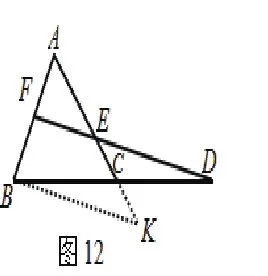
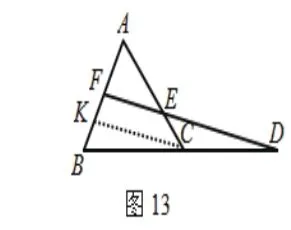
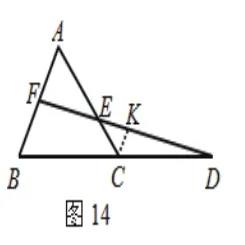
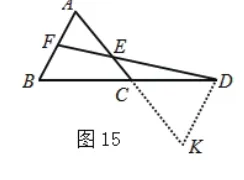
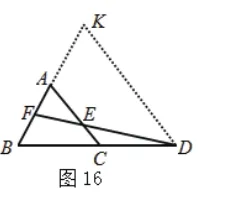
类似地，我们可以选取点B，以其为起点，可构造出两个图形（如图11、12）。选取点C，以其为起点，可构造出两个图形（如图13、14）。选取点D，以其为起点，可构造出两个图形（图15、16）。再选F，类似地可构造出三个图形（图略）。

四、方法归总

把从不同的点出发，引平行线进而构造相似三角形的所有情形归总起来列成表格：

起点 A B C D E F 合计种类 2 2 2 2 0 3 11

这样，就有11种不同的添加平行线的方案，从每个点出发都可以引出两条（或多于两条）平行线，不过此处一个显著的特点是：这里除了点E外，由其余各点引出的平行线均能与已知条件“CD=BC，F为AB的中点”沟通起来，或多或少地与比值有所牵连。为什么会出现这样的情况呢？这正如打算应用“全等三角形的对应边相等”来证明 “两条线段相等”，而在寻找全等的条件时，不能把需要证明相等的两边作为全等条件一样。这里我们不妨把点E称为“动”分点，而与之相对应的分点（包括线段的端点）称为“静”分点，我们据此得出下列规律和步骤：

（1）找出图中的所有分点（含线段端点），区分“动”分点和“静”分点；

（2）以每个“静”分点为起点，引平行线，构造相似三角形；

（3）在图中找出“A”字形和“X”字形图，并把它们从背景图中分离出来；

（4）根据“A”字形和“X”字形基本图中的基本结论，综合求出待求的比值。

五、应用举例

例1 如图17，△ABC中，BD∶DC=1∶3，AE∶ED=2∶3，求AF∶FC。

【解析】在A、B、C、D、E、F六个点中，点F是动分点，点A、B、C、D、E都是静分点。因此我们分别以A、B、C、D、E为起点引平行线，可以构造出以下图形（如图18、19、20、21等等，由于类同上述例题，所以构造出的其余图形不再画出）。这里同样有不下于10种引平行线的方法，最终可求得AF∶FC=2∶9。

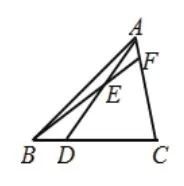
图 17

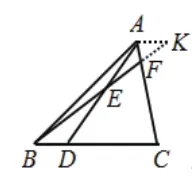
图 18

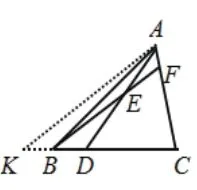
图 19

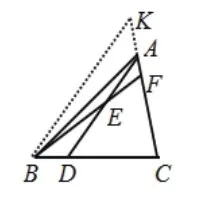
图 20

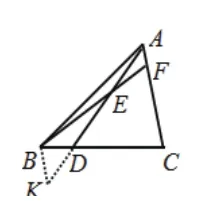
图 21

例2 如图22，在△ABC中，AB=AC，D为AB上的一点，E为AC延长线上的一点，且CE=BD，连接DE交BC于点P。

（1）求证：PD=PE；

（2）若CE∶CA=1∶5，BC=10，求BP的长。

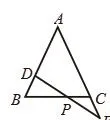
图22

【解析】（1）略。

（2）由于题中已知线段BC的长，欲求BP的长，只需求出BP∶BC的值即可。

观察图中的A、B、C、D、E、P六个点，点P为动分点，其余都是静分点，因此尝试从其他几个静分点出发引平行线构造相似三角形，分述如下：

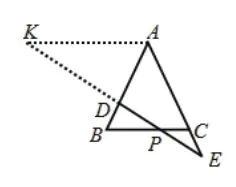
图 23

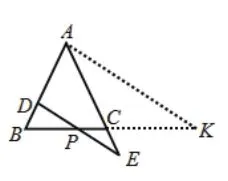
图 24

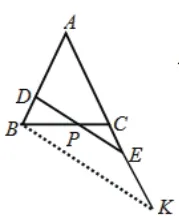
图 25

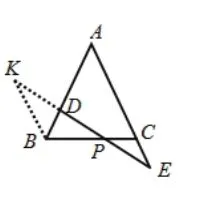
图 26

①以A为出发点，有如图23、24所示的两种构造方法。

②以B为起点，有如图25、26所示的两种构造方法。

以C、D、E为起点的构造方法类同，图略。

上述10种方案所构造的图形中，均包含有“A”字形或“X”字形基本图，通过分析其中的比例关系，不难求出BP∶BC=3∶5，所以BP的长为

数学解题能力的修炼和提高，得益于解题方法的积累和总结。在平时解题过程中不能只满足于就题论题，为解题而解题，也不要追求多解的数量，而要注重“多解归一”。文中所述各题，都是通过引平行线，进而对复杂图形进行拆分，利用其中的“A”字形或“X”字形相似，最终求出相关线段的比值。多角度地看待同一个问题，或同一角度看待不同的问题，最终达到“一题多解”或“多解归一”，这是修炼解题基本功的重要途径。作为教师，只有在解题教学中有意识地对学生加以培养和训练，才能使他们逐步提升能力，最终拥有常人所不具备的绝技，从而在解题竞技中“一招制敌”。

[1]罗峻，段利芳.一道平行线问题的证明、演变与运用[J].初中数学教与学，2017（19）.

[1]卢彩霞.利用解决平行线中拐角问题的方法求解折线成角问题[J].吉林教育，2017（37）.