这些易错点，你注意到了吗

河北省石家庄市鹿泉区第一中学 李志英

在高三复习的过程中，阶段性检测必不可少，作为一线教师，在阅卷及讲评过程中，发现学生的失分点并不仅仅是难题无法攻克，更多的失分是在简单题中对某个易错点忽视所造成的。下面以一次小测中学生暴露的问题为例，对易错问题进行总结。

一、“工具”应用有前提

例题：已知函数f(x)=|lnx|，若0＜a＜b，且f(a)=f(b)，则a+4b的取值范围是 _______________。

错因分析：本题借助基本不等式作为工具求最值时没有注意a的范围，根据函数图象可以判断a的范围是（0，1），而取等的条件是a=2，所以只能从函数单调性的角度考虑，发现在（0，1）上单调递减，所以a+4b的取值范围为（5，+∞）。

应对策略：借助基本不等式求最值时需关注“一正，二定，三等”，尤其是“三等”很容易忽视，如果不满足可以构造函数，分析单调性求解。

二、“字母”出现要小心

例题：已知集合A={x|ax2+bx-1=0}={1}，则由（a，b）组成的集合的子集的个数为（ ）

A.1 B.2 C .3 D.4

错解：由条件可知一元二次方程ax2+bx-1=0只有一个根1，即满足可得则由(a，b)组成的集合只有一个元素，即此集合的子集个数为2，选B。

错因分析：本题对字母参数取值需要讨论，当a=0时，此方程也可以有一个根1，当b=1时即满足条件。所以由(a，b)组成的集合含有两个元素，即此集合的子集个数为4，选D。

应对策略：牢记“遇到字母需谨慎，分类讨论是根本”，对于二次方程、函数、不等式出现字母时，对二次项系数需要特别关注。

三、“隐含信息”细思量

例题：已知锐角三角形ABC中，内角A，B，C所对应的边分别为a，b，c，且满足：b2-a2=ac，c=2，则a的取值范围为____________ 。

错解：由b2-a2=ac可得a2+c2-2ac .cosB-a2=ac，化简得2-2a·cosB=a，即因为B为锐角，所以0＜cosB＜1，即可得a的取值范围为（注：小猿搜题与作业帮软件中也是此答案）

错因分析：本题中背景是锐角三角形，要求三个角均为锐角或者最大角为锐角，错解中并未挖掘到B的范围限制，b2-a2=ac可以利用正弦定理和倍角公式进行转化如下：

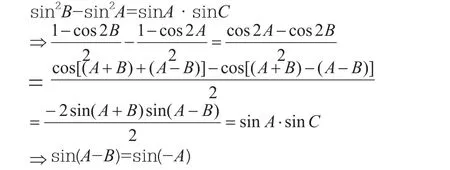
由于A，B为三角形的内角，即可得B=2A。由于三角形为锐角三角形，由此可得a的取值范围为（1，2）。

四、“特殊”情况不能忘

应对策略：对于圆锥曲线方程，需要“定型，定位，定量”三步考虑，标准方程的形式特征需要准确记忆。

通过上述分析会发现，学生的错误均属于思维不缜密所造成的，这与平时训练时纠错的处理有一定关系，没有挖掘到错误的根本，不能对易错点设立自己的“警示牌”，所以错误不断，总是遗憾。在这里也希望我们高三同学们能够“静下心来，在错误中寻找提分空间。动起手来，在重复中练就规范解答”。把会的题做对，该得的分必得，这样才能沉着地应对高考！