顶部带FPS-TMD系统的高耸结构风振控制效益分析
2018-03-28吴玖荣周泽宇梁强武傅继阳
吴玖荣, 周泽宇, 梁强武, 傅继阳
(广州大学-淡江大学 工程结构灾害与控制联合研究中心,广州 510006)
近年来随着我国经济的高速发展,各种类型的高层建筑和高耸结构与日俱增,上述结构也朝着轻质高强,柔细化低阻尼方向发展,因此水平荷载对其影响更为显著。相比与水平地震作用而言,风荷载作用时间更长,发生的频率相对更高,对于部分超高层建筑和高耸结构,风荷载往往成为影响其结构设计的主要控制因素。传统结构抗风设计主要通过增强结构刚度、材料强度以及塑形变形能力,加强节点构造等方式来改善。随着工程结构隔震减振技术的发展,多种隔震减振体系和方法应运而生,摩擦摆系统就是其中之一。
FPS(Friction Pendulum System)摩擦摆系统,是依靠圆弧曲面滑动耗能的干摩擦隔震系统(如图1所示),属于结构控制中被动控制中的一类。最早在1985年由Zayas等[1]提出,由于其具有良好的自复位等工程性能,在高层建筑、桥梁工程基础隔震中广泛采用。文献[2]中基于动力试验分析了FPS系统基底隔震的效果。该摩擦摆装置具有滑动阻尼装置的稳定性能,其独特的圆弧曲面提供了自限位、自复位[3-4]功能,滑块与滑动曲面之间是通过面之间的相互接触,通过圆弧面摩擦材料的摩擦耗能消散能量,常用的摩擦材料有聚四氟乙烯等。滑道可与地面连接,当基础部分受到水平地震作用时,地面的水平运动会使得滑块在其圆弧面做周期性滑动,然后滑块又可以在自身重力作用下复位,即返回圆弧滑动面的最底部,故不再需要附加额外阻尼装置,提高了装置的可靠度,这即为早期FPS在基础隔震中的应用。
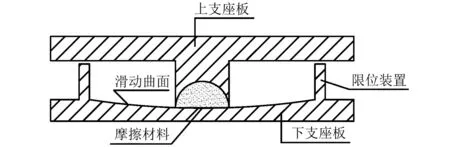
图1 摩擦摆隔震支座截面Fig.1 Bearing section of friction pendulum system
为减小结构受风扰动下产生的舒适度问题,Zhong等[5-7]将FPS系统置于高层建筑结构顶层,FPS系统装置的上部增加具有一定质量M的滑块形成FPS-TMD减振系统,通过研究其对结构的减振效益,探讨了加装FPS-TMD系统并对其进行最优化设计以达到最佳减振效果并考虑双重摩擦系统,同时针对FPS-TMD系统中的设计参数进行分析,探究减振之影响效果。文中以台北101塔为实例(如图2为分析对象),验证了FPS-TMD系统加装于结构顶层后此套装置的可行性。

图2 台北101塔Fig.2 Taipei 101
本文拟将FPS-TMD系统置于广州新电视结构顶层,通过建立其相应的简化有限元模型的基础上,建立整体动力方程,分析其风振效应。
1 FPS-TMD系统振动微分方程
1.1 FPS-TMD系统恢复力模型
FPS-TMD系统如图3所示,其中滑道半径为r,滑块质量为m,滑块相对于主体结构顶层运动的转角为φ,假定以逆时针转动方向为正。滑块m与滑动面的摩擦因数为μk,重力加速度为g,D为质量块相对结构顶层位移。
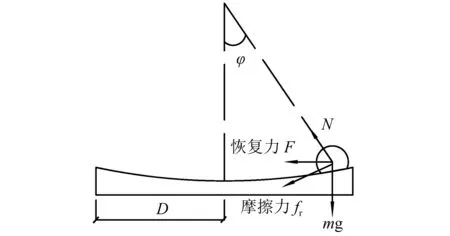
图3 FPS-TMD系统模型Fig.3 FPS-TMD system
利用滑块在某一时刻在滑道切向和法线方向的静力平衡条件建立方程,在滑道切线方向上
(1)
式中:fr为切向摩擦力
其在滑道法线方向上
N=mgcosφ
(2)
故水平方向上恢复力为
(3)
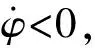
(4)
从式(4)可以看出,水平恢复力F由重力和切向方向摩擦力在水平方向分量组合组成,由重力产生的水平侧向刚度分量为k=mg/r, 鉴于FPS-TMD系统的恢复力特性具有非线性性质,可以采用等效线性刚度和等效黏性阻尼来描述FPS-TMD系统的统计力学特性[8], 依据式(4)FPS-TMD系统力和位移的简化滞回曲线如图4所示。故FPS-TMD系统的等效刚度为
(5)
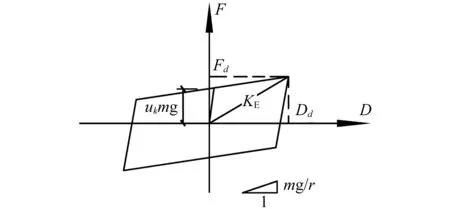
图4 FPS-TMD系统滞回曲线图Fig.4 Hysteresis curve for FPS-TMD system
FPS-TMD系统的自振圆频率为
(6)
FPS-TMD结构等效自振周期为
(7)
由式(7)可知FPS-TMD结构等效自振周期仅与滑道半径r,摩擦因数μk有关,调节周期依靠摩擦因数和滑道半径的改变,同时需要保证μkr/D为一个常数,与质量无关,故具有良好的稳定性能。FPS-TMD系统等效黏性阻尼比可用式(8)加以表达
(8)
式中:E为滞回耗散能量。
综合上面各式可知,当滑块相对于结构顶层运动的转角φ很小时,模型近似为一个平面滑移带复位弹簧的阻尼装置,相比之下FPS-TMD系统靠重力复位,平面滑移带复位弹簧的阻尼装置则必须依靠附加的弹簧件复位,FPS-TMD系统当滑动机构有微小倾斜时,不会影响系统的正常工作,而在平面滑移带复位弹簧的阻尼装置中,滑板的微小倾斜将导致滑动位移偏向下斜的方向。此外FPS-TMD系统依靠滑道摩擦因数μk的变化, 当μk值采用中间小两边大的形式设置时,限制了滑块的位移,不需要额外加装限位系统,同时无悬挂摆线,极大地释放了净空高度,相比之下优势较为明显。
1.2 FPS-TMD系统振动特性
摩擦摆调谐质量阻尼器FPS-TMD系统如受到地震作用或风荷载激励下会产生振动,为不失一般性本文用外加风荷载p(t)分析如下。
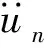
(9)
滑道在其切线方向的动力平衡方程为
(10)
将式(9)、式(10)合并,方程两端同时除以mr, 化简可得FPS-TMD振动微分方程
(11)
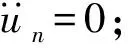
(12)
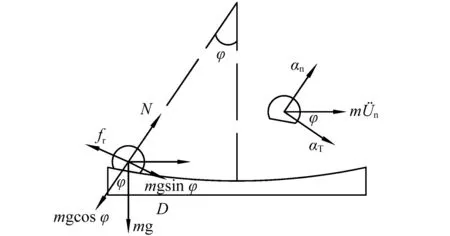
图5 FPS-TMD自治振动力学模型Fig.5 Mechanical model for FPS-TMD vibration system
2 顶部带FPS-TMD系统的整体结构动力方程
为便于理论推导分析,本部分将顶部带FPS-TMD系统的整体结构采用简化集中质量的平面模型来进行处理,首先将主体结构简化成一个N层即N个自由度的框架模型,每一层具有质量mi、层间刚度ki和阻尼系数ci,(i=1,2,…,n)。FPS-TMD系统置于主体结构顶层之上,FPS-TMD系统的质量md,切线刚度系数kd,坐标系采用如图6所示的vOu系统,主体结构受风荷载激励p(t),等效作用于各个楼层集中质量处。为此建立结构的动力方程为
(13a)
式中: [M]、[C]、[K]分别为主体结构质量矩阵、刚度矩阵和阻尼矩阵; {FTMD}为FPS-TMD系统对主体结构的控制力,是一个N维列向量,即等于FPS-TMD系统的惯性力
(13b)
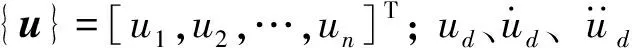
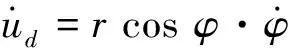
(14)
主体结构阻尼矩阵的构造方法采用扩展的Rayleigh阻尼[10],便于方程解耦以及构造结构阻尼矩阵的准确性,即
(15)
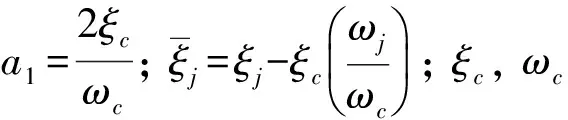
(16)
式(16)与上节得出的振动方程式(11)应具有一致性,当φ很小趋近于0时, cosφ=1,联立式(16)、式(11)并与式(14)比较,且式(16)中的md和式(11)中的m取值相同时, 可得FPS-TMD系统广义振动方程中的kdud为
(17)
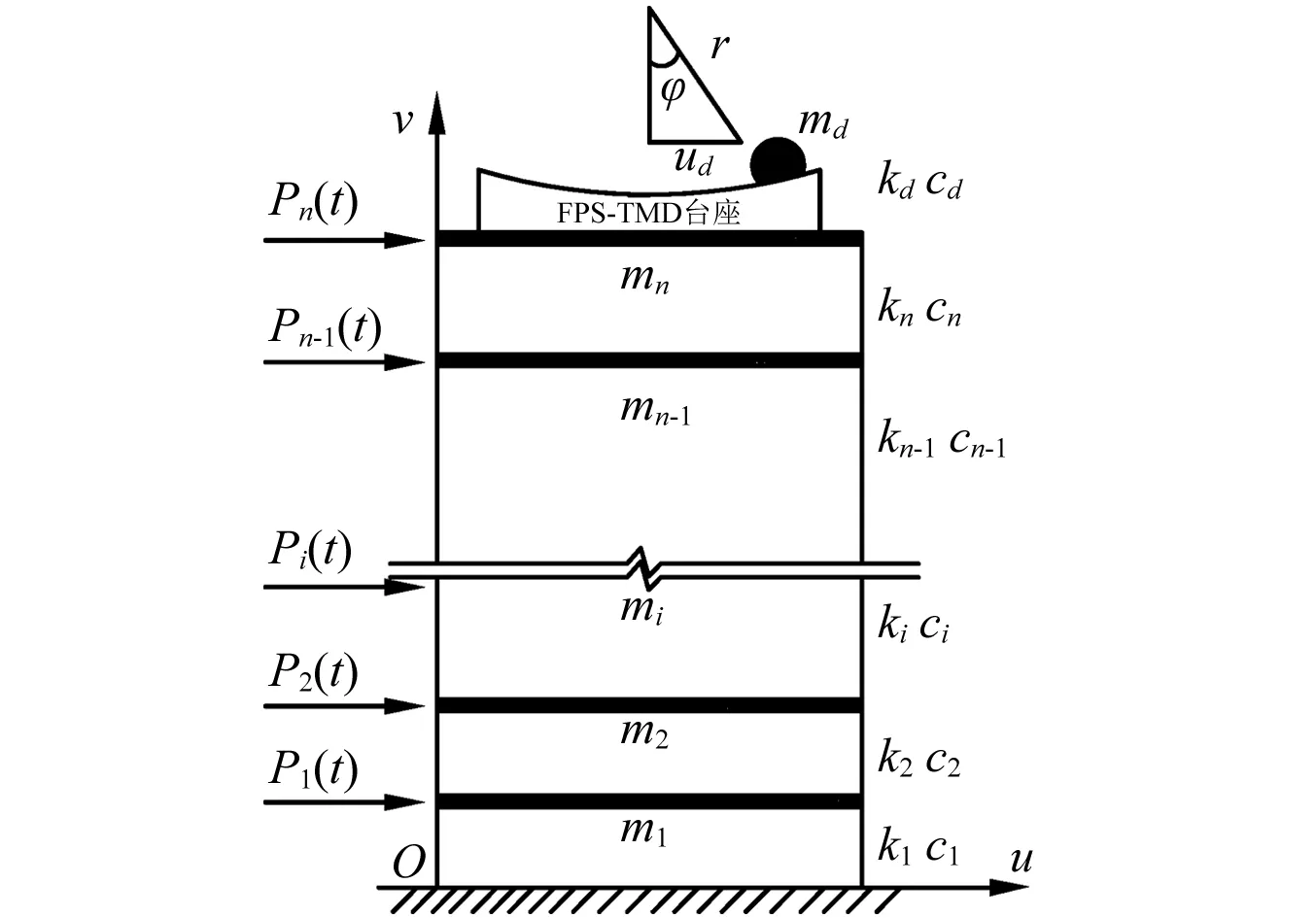
图6 顶部带FPS-TMD系统的整体结构示意图Fig.6 Building structure with supplemental FPS-TMD system
联立式(13a)、式(16)可得顶部带FPS-TMD系统的整体结构动力方程为
(18)
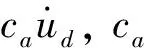
(19a)
其中,
(19b)
3 顶部带FPS-TMD系统的整体结构动力方程组求解及迭代处理
顶部带FPS-TMD系统,其非线性特征明显,外部风荷载激励p(t)变化复杂,对于微分方程式(19a),一般的求解动力反应的时域分析或频域分析方法等对求解线性方程组较为有效。对于结构体系具有非线性性质时,叠加原理不再适用,故本文采用时域逐步积分法中的Newmark-β法求解联立的动力反应方程组。
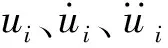
(20)
指定公差Tol,当Tol
4 实例计算
为验证和分析顶部带FPS-TMD控制系统的高耸结构风振控制和减振效果,本文以广州新电视塔(见图7)为研究对象,采用MATLAB软件(版本R2014a)编制了动力时程分析等相关风振控制分析程序。广州新电视塔建筑总高度600 m,结构主塔高度450 m,天线桅杆150 m,核心筒为钢筋混凝土筒体,外筒体为钢结构斜交网格支撑体系,两者之间由水平钢梁及组合楼板相连。
由于广州新电视塔整体结构有限元模型自由度数量庞大,其三维有限元模型共有23 851个板壳单元,18 757个框架单元,28 253个节点单元。
为简化动力分析的计算工作量,本文采用对原三维有限元模型进行降阶处理的方法,模型降阶后的简化结构模型成为37个节点,每个节点包含5个自由度,共185个自由度的糖葫芦串模型[11-12],如图7所示。这样使得求解动力方程的自由度减小,储存带宽大大缩减,提高了计算效率,缩小了计算分析的存储空间。
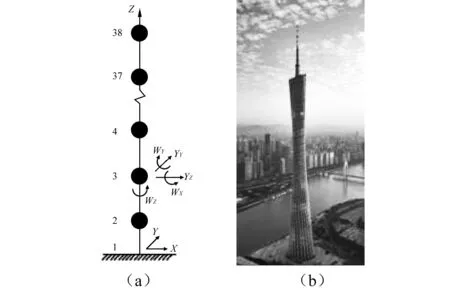
图7 广州新电视塔与简化模型Fig.7 Simplified FE model for the canton tower
简化后的广州新电视塔模型为具有37个梁单元和38个节点的悬臂梁模型,电视塔主塔由27个单元组成而桅杆部分由10个单元组成。简化模型中梁单元的质心与桅杆的质心在竖向投影方向一致。简化模型中的竖向位移忽略不计,这样每个节点具有5个自由度,分别是两个水平方向的平动(x,y)以及3个方向的转动(θx,θy,θz)[13]。
经降阶后后,广州新电视塔简化模型的动力特性与原三维有限元模型对比如表1所示,对比结果表明,简化模型的频率及振型与原三维模型在前6阶基本保持一致,因高耸结构的风致响应以整体前几阶响应为主,因此可采用简化模型进行风振分析。
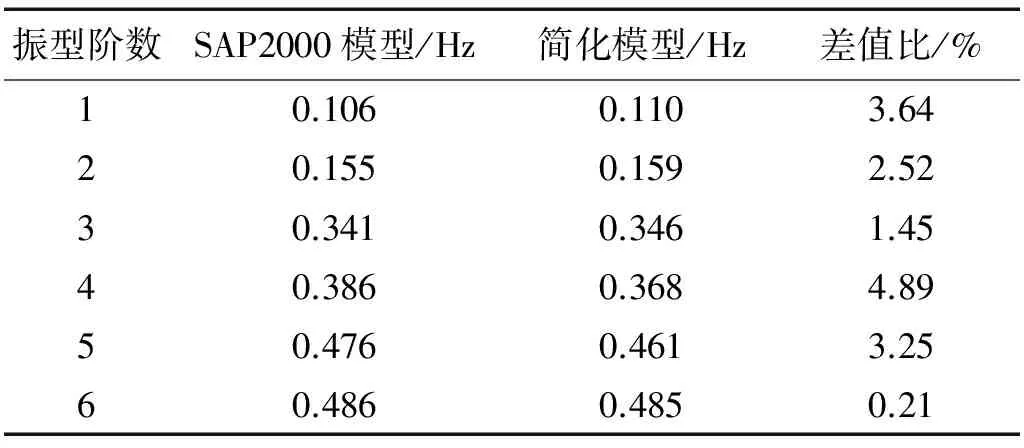
表1 简化模型与三维模型自振频率
用动力时程分析计算结构风致响应,需要输入外部风荷载时程p(t), 本文风荷载模拟采用谐波叠加法,对广州新电视塔在90°风向角沿塔体高度竖向分布的顺风向风荷载进行了模拟,设定时间步长0.5 s,持续1 024 s。脉动风速分布采用沿高度变化的Von Karman谱,采用快速傅里叶变换和谐波叠加法,进行脉动风速时程模拟,进而得到顺风向脉动风速时程沿高分布,依据风洞实验得到的风荷载体型系数把脉动风速转化成风荷载后输入结构体系中[14]。然后对式(19a)所示的动力方程组采用Newmark-β法求解。设计风速采用100年重现期和10年重现期两种,前者主要用于进行主体结构顶部风致位移分析,后者则主要用于主体结构顶部风致加速度(舒适度)分析。
5 顶部带FPS-TMD系统的风振控制效率分析
5.1 不同结构阻尼比下减振效益分析
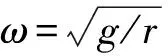
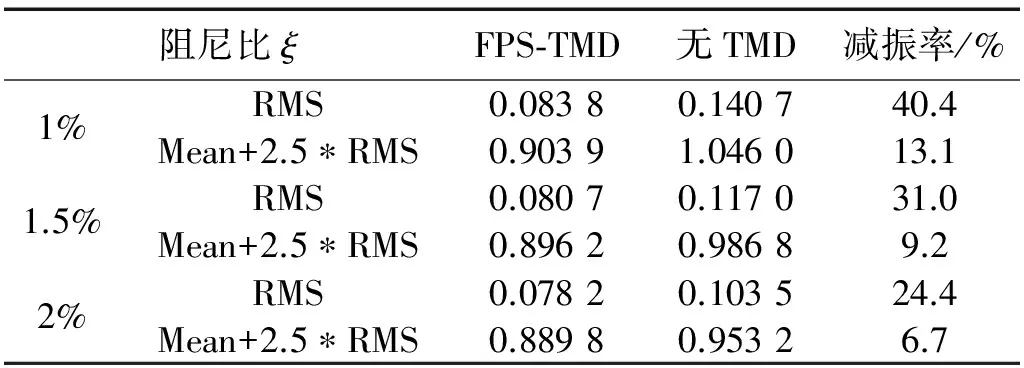
表2 100年重现期风速不同阻尼比结构顶层位移
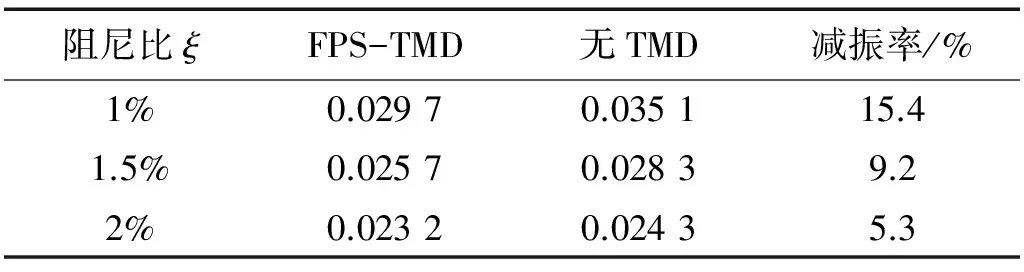
表3 10年重现期风速不同阻尼比结构顶层加速度
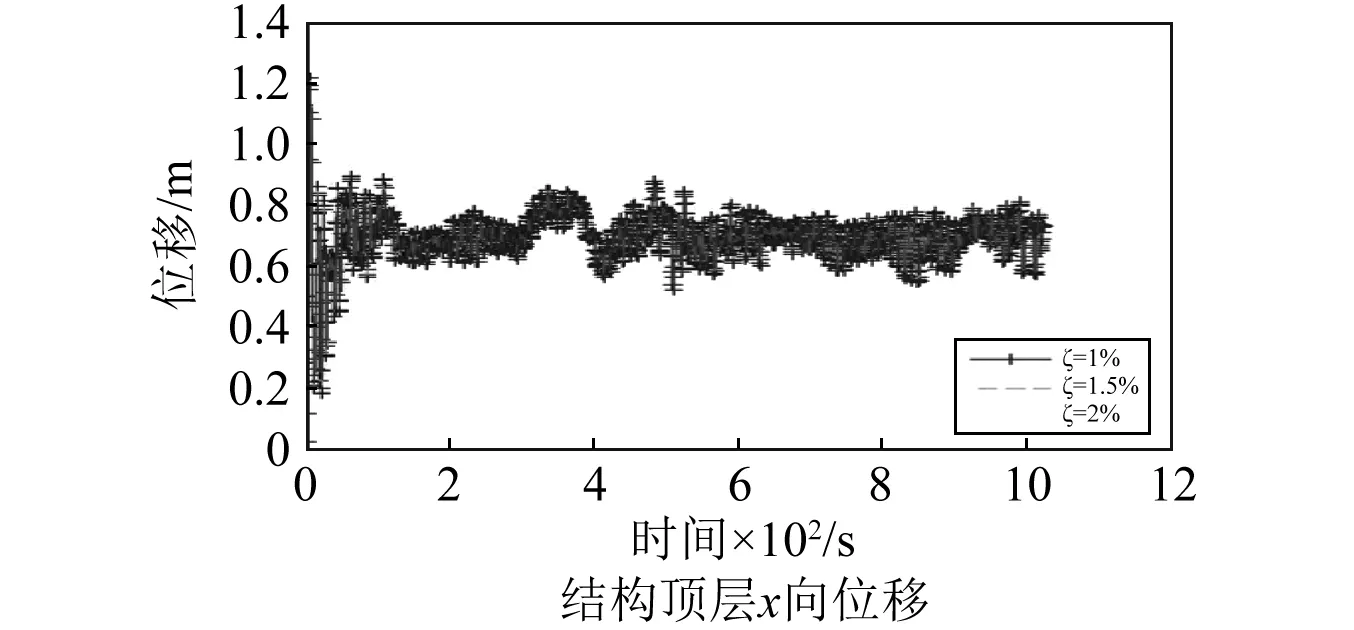
图8 100年重现期风速不同阻尼比结构顶层位移时程Fig.8 Time history of wind-induced displacement atop of the main structure
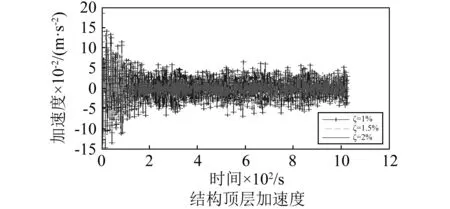
图9 10年重现期风速不同阻尼比结构顶层加速度时程Fig.9 Time history of wind-induced acceleration atop of the main structure
从表2表3可以看出,结构顶层位移均方根、顶层加速度均方根随结构阻尼的增大而减小,当仅计入均方根响应时,顶部装备有FPS-TMD系统后其减振效果明显,在阻尼比1%情况下,结构位移均方根减振率可高达40.4%,加速度均方根减振率达15.4%。
5.2 不同质量比下减振效益分析
假定FPS-TMD系统阻尼比ξ=1.5%,滑道半径取主体结构第一阶自振频率0.11 Hz下对应的值r=20.5 m,摩擦因数μk=0.01, FPS-TMD系统质量md与结构总质量之比取不同值时分析结果如表4,表5所示。
从表4和表5可以看出,主体结构顶层位移均方根随FPS-TMD系统质量与结构总质量比的增大而减小,质量比越大,减振效果越好;同时顶层加速度均方根也随质量比的增大而减小;说明FPS-TMD质量越大,减振效果越好。

表4 100年重现期风速下不同质量比顶层位移均方根

表5 10年重现期风速不同质量比顶层加速度均方根
5.3 不同动摩擦因数下减振效益分析
假定FPS-TMD系统阻尼比ξ=1.5%, 滑道半径取主体结构第一阶自振频率0.11 Hz下对应的值r=20.5 m, FPS-TMD系统质量md与结构总质量之比α=md/M固定为1%;则取不同摩擦因数下分析结果如表6,表7所示。
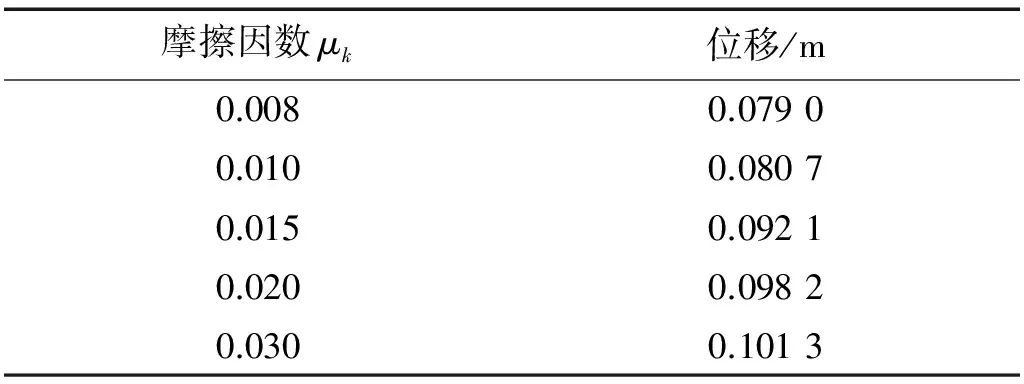
表6 100年重现期风速下不同摩擦因数顶层位移均方根

表7 10年重现期风速下不同摩擦因数比顶层加速度均方根
从表6,表7可以看出,结构顶层位移均方根、顶层加速度均方根随FPS-TMD滑道摩擦因数μk的增大而增大。可说明摩擦因数越大,周期越小,减振效率与其成反比。
5.4 不同滑道半径r下减振效益分析
假定FPS-TMD系统阻尼比ξ=1.5%, FPS-TMD系统质量md与结构总质量之比α=md/M为1%;摩擦因数μk=0.01,当采用不同滑道半径r时,其减振效果结果如表8,表9所示。
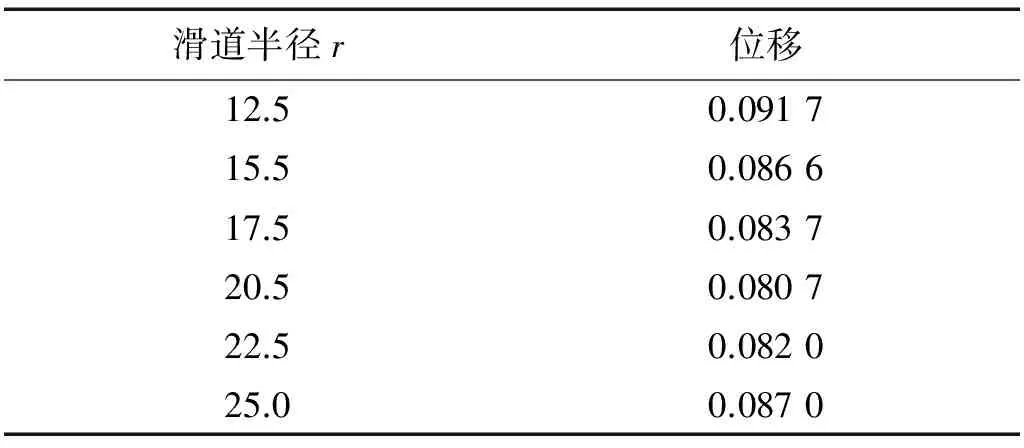
表8 100年重现期下不同滑道半径结构顶层位移均方根
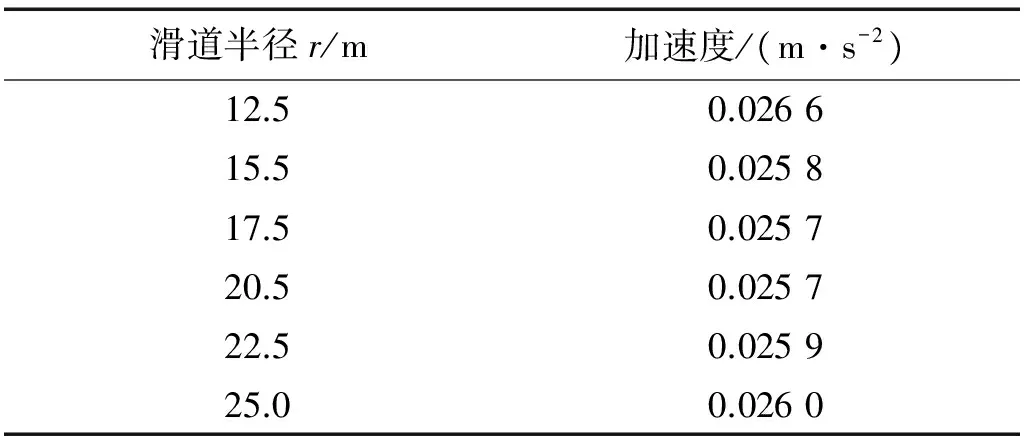
表9 10年重现期不同滑道半径结构顶层加速度均方根
从表8,表9可以看出,结构顶层位移均方根、顶层加速度均方根随FPS-TMD滑道半径r的增大而减小,滑道半径越大位移减振效果越好,周期越接近第一阶频率效果越好,但对加速度控制作用效果不明显。
6 结 论
本文在推导顶部带FPS-TMD系统的高耸结构,在风荷载作用下动力平衡方程的基础上,以广州新电视塔为例,通过选用影响其控制效益的不同参数作用下的风致位移和加速度对比,对上述FPS-TMD系统的风振控制效果进行分析,可得出如下结论:
(1) FPS-TMD系统对具有不同阻尼比的主结构具有不同的减振效率,主体结构阻尼越小其减振效果越明显。相比无FPS-TMD系统结构的风振响应而言,数值分析表明,主体结构阻尼比为1%时,100年重现期结构顶层位移均方根减振可高达40.4%,10年重现期风速下结构顶层加速度均方根减振可达15.4%。
(2) 通过合理选择FPS-TMD系统的控制设计参数如:质量比、阻尼比、滑道半径、摩擦因数等,可使得主体结构能够达到最佳减振效率。
(3) 顶部带FPS-TMD系统对主体结构的风振控制效果明显,特别是针对以风致振动为第一阶振型为主的高层柔性结构,效果较为显著。
(4) FPS-TMD系统可以有效地减少风荷载对主体结构的风致振动响应,与此同时FPS-TMD系统具有良好的稳定性和自复位、自限位功能。故FPS-TMD系统确实为一种有效的被动减振装置。
(5) FPS-TMD系统需合理选取参数后,可加装于主体结构顶层部位,根据本文计算,选取大概长宽各4 m左右、高度1 m左右台座作为系统下支座板,并在其上滑道曲面上填涂聚四氟乙烯或其它低摩擦材料。上支座板为质量块,采用高密度材料长方体如长宽高分别为8 m、8 m、3 m,如图1所示。质量为结构总质量1%,上支座板下部为直径为2 m圆柱面,与下支座板接触部位与滑道半径曲率一致,保证其滑动,整体安装与结构顶层部位。同时,上支座板可作为使用平台合理利用。
[ 1 ] ZAYAS V, LOW S S, MAHIN S A. A simple pendulum technique for achieving seismic isolation [J]. Earthquake Spectra,1990, 6(2): 317-331.
[ 2 ] MOKHA A S, CONSTANTINOU M C, REINHORN A M, et al. Experimental study of friction pendulum system isolation system [J]. Journal of Structural Engineering, 1991, 117(4): 1201-1217.
[ 3 ] 李大望,王东炜,周锡元.FPS自治系统及其性态分析[J].振动与冲击,1999,18(1): 23-25.
LI Dawang, WANG Dongwei, ZHOU Xiyuan. FPS autonomy system and behavior analysis[J].Journal of Vibration and Shock, 1999, 18(1): 23-25.
[ 4 ] 李大望,周锡元,霍达,等.FPS隔震结构的性态和地震反应分析[J].工程抗震,1996(1): 6-9.
LI Dawang, ZHOU Xiyuan, HUO Da, et al. FPS morphology and seismic response of isolated structure [J]. Earthquake Resistant Engineering, 1996(1): 6-9.
[ 5 ] ZHONG L L, WU L Y, LIEN K H, et al. Optimal design of friction pendulum tuned mass damper with varying friction coefficient [J]. Structural Control & Health Monitoring, 2013, 20(4): 544-559.
[ 6 ] 钟立来,吴赖云,陈宣宏,等. 摩擦钟摆型调谐质块阻器之优化研究[J]. 中国土木水利工程学刊, 2011, 23(1): 11-23.
ZHONG Lilai, WU Laiyun, CHEN Xuanhong, et al. Optimal design of friction pendulum typed tuned mass damper [J]. China Civil Engineering Society, 2011, 23(1): 11-23.
[ 7 ] 林廷翰. 双向摩擦钟摆型调谐质块阻尼器减振效益之研究[D]. 台北:台湾大学,2009.
[ 8 ] 杨林,周锡元,苏幼坡,等. FPS摩擦摆隔震体系振动台试验研究与理论分析[J].特种结构, 2005, 22(4): 43-46.
YANG Lin,ZHOU Xiyuan,SU Youpo, et al. Theoretical and experimental study on friction pendulum isolated system [J]. Special Structures, 2005, 22(4): 43-46.
[ 9 ] 潘琴存. 摩擦摆TMD减震结构的动力分析与试验研究[D].武汉:华中科技大学, 2006.
[10] 爱德华·L·威尔逊. 结构静力与动力分析——强调地震工程学的物理方法[M].上海:中国建筑工业出版社, 2006.
[11] 顾明,黄鹏,周晅毅,等.广州新电视塔模型测力风洞试验及风致响应研究I:风洞试验[J]. 土木工程学报, 2009, 42(7): 8213.
GU Ming, HUANG Peng, ZHOU Xuanyi, et al. Wind tunnel force balance test and wind-induced responses of the Guangzhou new TV tower structureⅠ: wind tunnel test [J]. China Civil Engineering Journal, 2009, 42(7): 8213.
[12] 周晅毅,顾明,朱乐东,等.广州新电视塔模型测力风洞试验及风致响应研究Ⅱ:风致响应分析[J].土木工程学报, 2009(7): 14-20.
ZHOU Xuanyi, GU Ming, ZHU Ledong, et al. Wind tunnel force balance test and wind-induced responses of the Guangzhou new TV tower structure Ⅱ : analysis of wind-induced responses [J]. China Civil Engineering Journal, 2009(7): 14-20.
[13] CHEN W H, LU Z R, LIN W, et al. Theoretical and experimental modal analysis of Guangzhou new TV tower [J]. Engineering Structures, 2011, 33(12): 3628-3646.
[14] 胡嘉伟. 带TMD系统高耸结构风振控制效益分析[M]. 广州:广州大学,2016.
