三磁体型隔振器的性能分析和实验研究

柴 凯， 朱石坚, 杨庆超， 刘树勇

(1. 海军工程大学 动力工程学院，武汉 430033；2. 海军工程大学 船舶振动噪声重点实验室，武汉 430033)

声隐身技术是提高潜艇水声对抗性能的关键技术之一。降低潜艇辐射噪声，不仅可改善其隐身性能，还能提高艇载水声探测设备的探测能力，从而大大提高潜艇的战术技术性能[1]。机械设备振动是潜艇低速隐蔽航行时的主要噪声源，而隔振是减小机械振动向艇体传递、降低水下辐射噪声的最有效手段。为了提高隔振效果，Carrella等[2]进行了广泛深入的研究，一方面是降低隔振系统的刚度，但此时系统的静变形较大，稳定性差；另一方面是采用主动控制，但对于设备质量较大、安装空间狭小的潜艇舱室环境，现有作动器难以满足工程需求，而且主动控制系统存在结构复杂、能量消耗较大等不利因素，在能量较为宝贵的潜艇上难以取得满意的效果[3]。

高稳定性和低固有频率一直是传统隔振系统的矛盾，由于潜艇机械设备隔振系统对稳定性要求较高，传统被动隔振系统固有频率降低的程度有限，制约着被动隔振系统隔振效果的进一步提升。准零刚度隔振器是通过合理设计负刚度机构的几何和刚度参数，将正负刚度弹性元器件并联在静平衡位置获得零刚度的组合隔振器[4]。相比传统的线性隔振器，准零刚度隔振器具有高静刚度低动刚度的特性，能有效解决大承载力和超低频隔振、超低刚度和位置稳定性、低频振动传递率和高频振动衰减率不可兼顾的矛盾[5]。实现准零刚度隔振技术的关键在于负刚度机构的设计和计算[6]，基于永久磁铁或电磁铁的负刚度机构因为无机械摩损、噪声小、无需润滑、可引入半主动控制调节系统刚度和承载能力不受负刚度机构影响等优点，引起了国内外学者广泛的关注。Zhou等[7]将结构梁、电磁铁和永久磁铁并联设计了隔振器，通过调节电流的方向实现隔振器的半主动控制；Li等[8]通过磁环与橡皮膜结合设计了负刚度隔振器；Tao等[9]设计了六自由度的磁悬浮型准零刚度隔振系统；Shan等[10]利用气囊和磁环结合设计了一种新型空气弹簧减振器；Zheng等[11]对基于永磁铁和电磁铁的准零刚度隔振器进行了深入研究；Xu等[12]采用垂直线性线圈弹簧和两个对称的磁力弹簧组合设计了磁力准零刚度隔振器。但上述文献主要采用环形磁铁或磁砖，磁铁间隙调节困难，负刚度的变化范围有限。

本文通过建立矩形磁铁的磁力和刚度解析模型，分析其负刚度特性，通过仿真优化矩形磁铁尺寸参数，将其应用于三磁体型隔振器，并对其动力学特性进行分析，探索系统参数对减振性能的影响规律，为评估实际隔振性能，进行一系列的实验分析。

1 矩形磁铁的磁力解析模型

1.1 点磁荷磁场强度的计算

如图1所示，面积为2a×2b矩形磁面，依据等效磁荷理论[13]，任意一点P的标量磁位的二维泊松方程

(1)

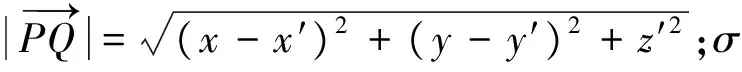
(2)

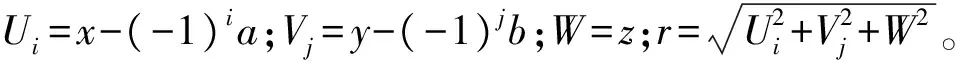
(3)

对于体积为2a×2b×2c矩形磁铁，被磁化后各磁偶极子在磁铁内部均匀排列，N极和S极首尾相连，只在两个端面出现单一的正或负磁荷。由静磁学理论[14]，

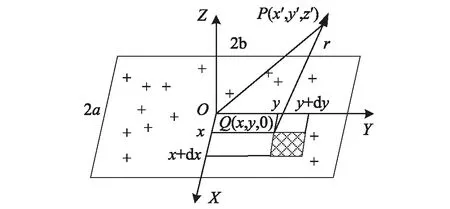
图1 矩形磁面对点P的磁标量势Fig.1 Magnetic scalar potential of a rectangular surface in the point P

当充磁方向与磁铁表面法线重合，钕铁硼永磁材料的介质极化强度J，面磁荷密度σ和剩余磁感应强度Br三者相等。根据H=-φP，在场点P对φP求梯度，可得点P磁场强度

(4)

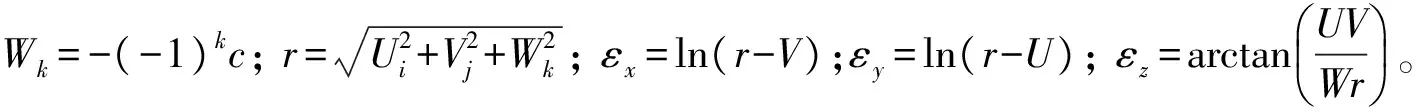
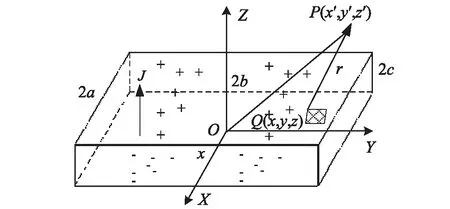
图2 矩形磁体对点P的磁标量势Fig.2 Magnetic scalar potential of a rectangular magnet in the point P

1.2 矩形磁铁的磁力和刚度解析模型

设上下磁铁均均匀充磁，下磁铁尺寸为2a×2b×2c，介质极化强度为J，所在坐标系为O-XYZ；上磁铁尺寸为2a′×2b′×2c′，介质极化强度为J′，方向与下磁铁相同，所在坐标系为O′-X′Y′Z′，O′的坐标为(x,y,z)。

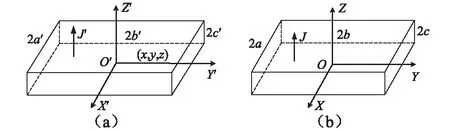
图3 两块矩形磁铁的几何模型Fig.3 Two parallelepiped magnets configuration

根据等效磁荷理论，两块磁铁间的磁力由上、下磁铁的上、下端面相互作用产生，两块充磁方向平行的静磁能

(5)

(6)

经四重积分后可得

(7)

式中：η=i+j+k+l+p+q。

（3）建筑质量差：土坯建筑、彩钢房、荒废失修的破败建筑等，根据村民需求和意愿原地重建，确定需要原地重建的住宅建筑数量。

(8)

根据虚功原理[15]可得两磁铁间的磁力

(9)

当上下磁铁充磁方向相同时F取正，反之则F取负，省略多重求和为零的项

(10)

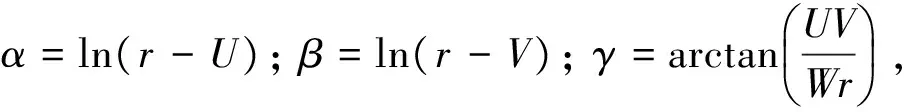
(11)

式中：τx=Ulnβ+r;τy=Vlnα+r;τz=-2r-Ulnβ-Vlnα。

1.3 有限元仿真验证

利用ANSYS Maxwell有限元软件对三磁体的磁力进行计算，并与解析表达式结果进行对比验证。图4是不同位置磁场强度分布图，由图5可知，在平衡位置所受磁力为0，有限元仿真结果与三磁体磁力解析模型结果吻合较好，验证了本文推导的磁力解析模型的准确性。

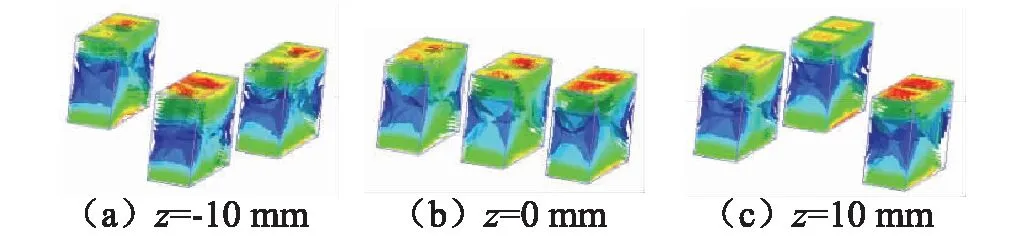
图4 不同位置的磁场强度Fig.4 Magnetic intensity at the different positions

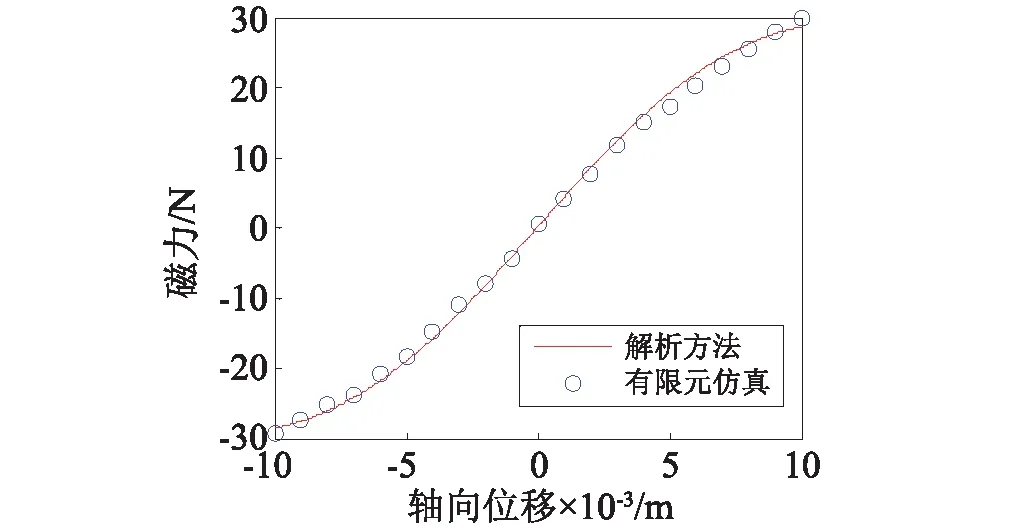
图5 磁力-位移曲线解析模型和有限元方法的对比Fig.5 Comparison of the magnetic force-displacement between analytical model and finite element method

2 磁铁尺寸的优化与设计

由上述分析可知，矩形磁铁的刚度与磁铁相对位置、充磁方向、几何参数和剩余磁感应强度等密切相关。如图6所示，三磁体沿Z轴间隔l布置，外部磁铁尺寸为2a×2b×2c，中间磁铁尺寸为2a′×2b′×2c′，充磁方向均沿Z轴正方向，中间磁铁沿轴上下运动时，由式(11)可得Kz=-2Kz(0,l,z)。为了更好地匹配正刚度，矩形磁铁在获得较大负刚度的同时，还应具有较好的线性特征，需要三磁体几何尺寸进行优化。

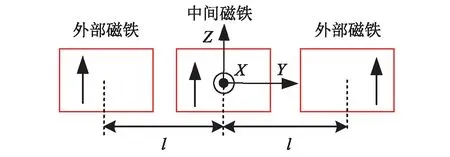
图6 三磁体的布置示意图Fig.6 Schematic configuration of the tri-magnets

考虑磁铁布置方式和总体结构，设三磁体的初始尺寸均为40 mm×20 mm×30 mm，l=30 mm，下面采用控制变量法分析外部磁铁几何尺寸的变化对中间磁铁Z向负刚度的影响。维持b,c不变，a在10～30 mm内间隔0.01取值，由图7(a)可知，负刚度随着a的增加而增加，线性特征变小。维持a，c不变，b在1～20 mm内间隔0.01取值，由图7(b)可知，负刚度随着b的增加而增加，且存在突变，线性特征变小。维持a，b不变，c在10～20 mm内间隔0.01取值，由图7(c)可知，负刚度随着c的增加先增加后减小，在c=15 mm达到峰值，线性特征先减小后增大。因此，综合考虑负刚度的大小和线性特征，取中间磁铁的尺寸40 mm×20 mm×30 mm，外部磁铁的尺寸35 mm×18 mm×20 mm。

3 三磁体型隔振器的动力学模型

Kz的积分表达式不利于建立系统的动力学方程，由图8可知，在三磁体几何尺寸确定的前提下，负刚度可以表示为关于z的二阶多项式，同时由于刚度大小也与磁铁间距l有关，故可设负刚度的表达式为

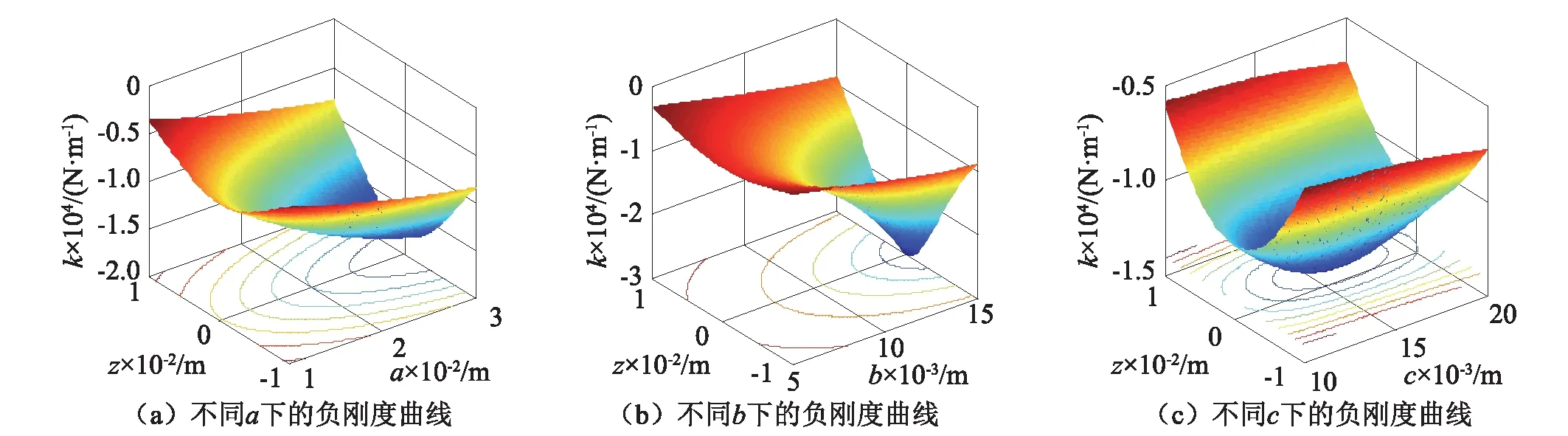
图7 尺寸参数对负刚度的影响Fig.7 Effect of dimension parameters on negative stiffness

Kz=k1(l)+k2(l)z2

(12)

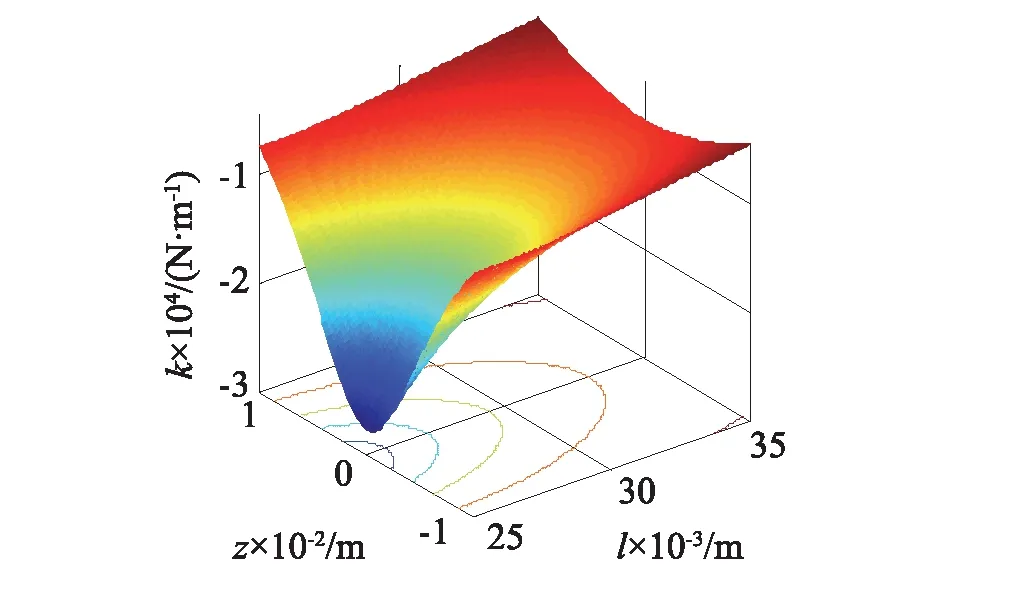
图8 不同磁铁间隔下的负刚度曲线Fig.8 Negative stiffness curve at the different gaps

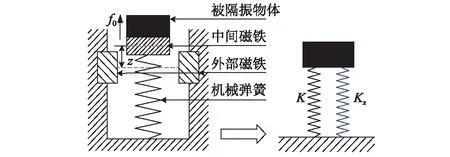
图9 三磁体型隔振器的结构示意图Fig.9 Schematic diagram of tri-magnets vibration isolator

隔振器的动力学方程可表示为

(13)

式中：c为系统的阻尼系数;m为被隔振物体的质量;K为机械弹簧的刚度。将式(13)无量纲化

(14)

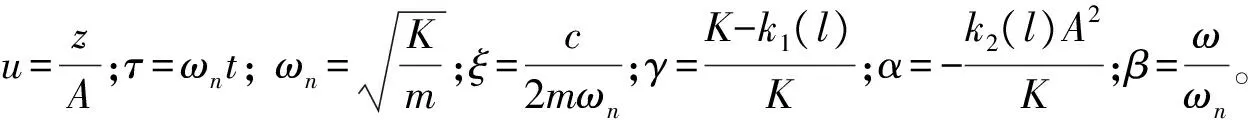
(15)

从而推出系统的幅频方程

(16)

通过三磁体型隔振器传递地基的力ft

(17)

从而得到简谐力激励下系统的传递率

(18)

去掉外部磁铁，得等效线性系统的传递率

(19)

由式(18)可知系统的力传递率与激励幅值A和阻尼比ξ密切相关。图10给出了不同激励幅值时三磁体型隔振系统与等效线性系统力传递率曲线的比较。由图10可知，随着激励幅值递增，三磁体型隔振系统传递率峰值和共振频率均增加，当激励频率较高时，传递率趋于一致；而对于等效线性系统而言，随着激励幅值的递增，系统的传递率峰值和共振频率均不变。

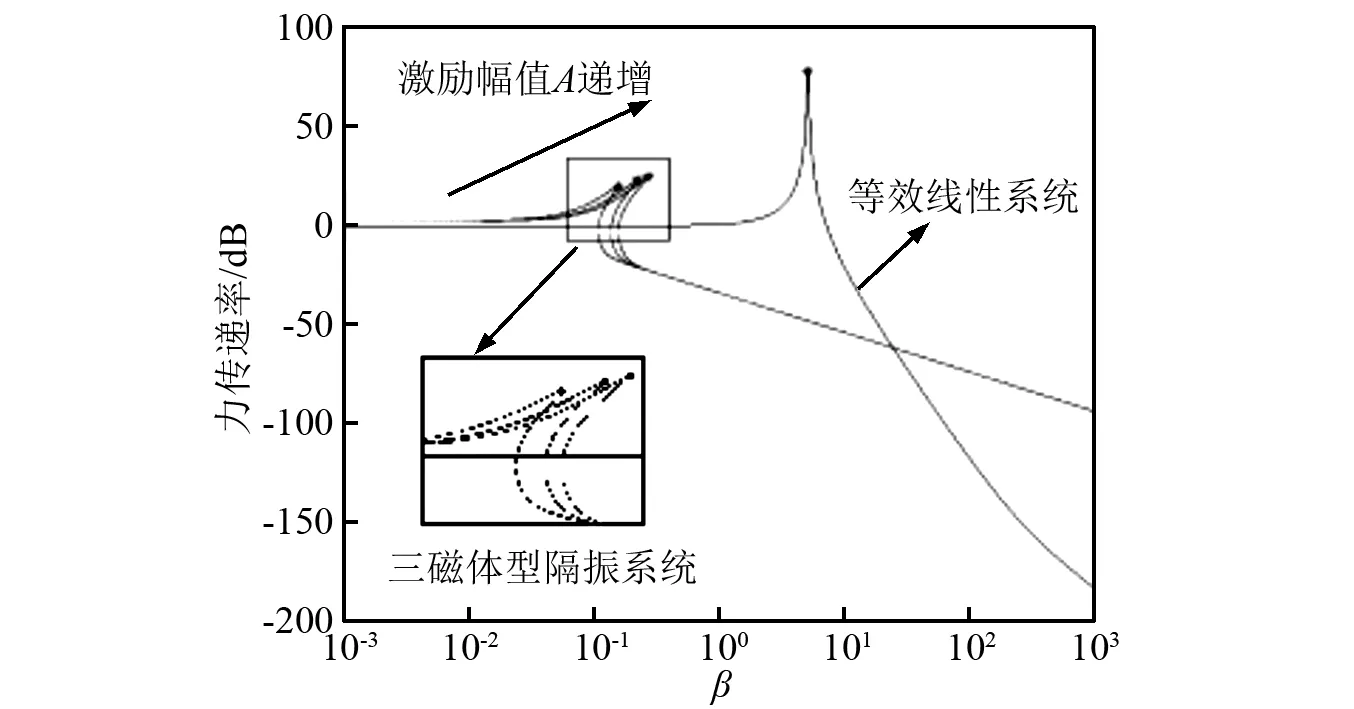
图10 激励幅值对系统力传递率的影响Fig.10 Effect of excitation amplitude on force transmissibility

图11给出了不同阻尼比时系统的传递率曲线。有图可知随着阻尼比的递增，三磁体型隔振系统的传递率峰值和共振频率均减小，但阻尼比过大会影响高频段的正负刚度并联系统的隔振性能；而对于等效线性系统而言，随着阻尼比的递增，系统的传递率峰值减小，但共振频率不变。图10和图11表明：相比等效线性系统，三磁体型隔振系统的隔振起始频率更低，隔振频带更宽，传递率峰值更小，低频隔振性能更优越。

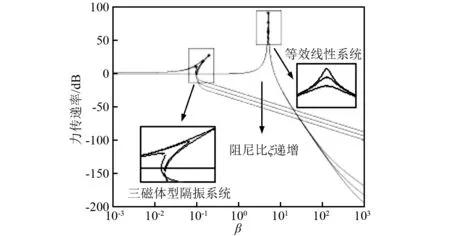
图11 阻尼比对系统幅频特性的影响Fig.11 Effect of damping ratio on force transmissibility

4 实验研究

三磁体型隔振器振动实验装置和数据采集系统如图12所示，其相应参数如表1所示。它主要包括三磁体型隔振器、激振器、2个阻抗头(包含力传感器和加速度计)、功率放大器、数据采集分析仪等。三磁体型隔振器结构沿中心轴线呈对称，上盖开设定位销，以保证中心轴的对中性，底座凸台和调节套可保证机械弹簧的垂直度，滑动轴承固定在上盖端部，与中心轴的配合能限制中心轴的径向运动，配重固定在载物台的正中央。在激振器和平衡质量块之间放置阻抗头1，用以测量激励的力大小，在上盖顶端放置另一个阻抗头，用以测量传递到基础的力大小。

图12 实验装置及数据采集系统Fig.12 Experimental apparatus and data acquisition system

三磁体型低频隔振器实验模型在平衡位置附近的刚度曲线如图13所示。由图13可知，在静平衡位置处，系统刚度为零；在静平衡位置附近的小振幅区间内，系统刚度较小，具有高静低动的刚度特性。

表1 实验装置的物理参数

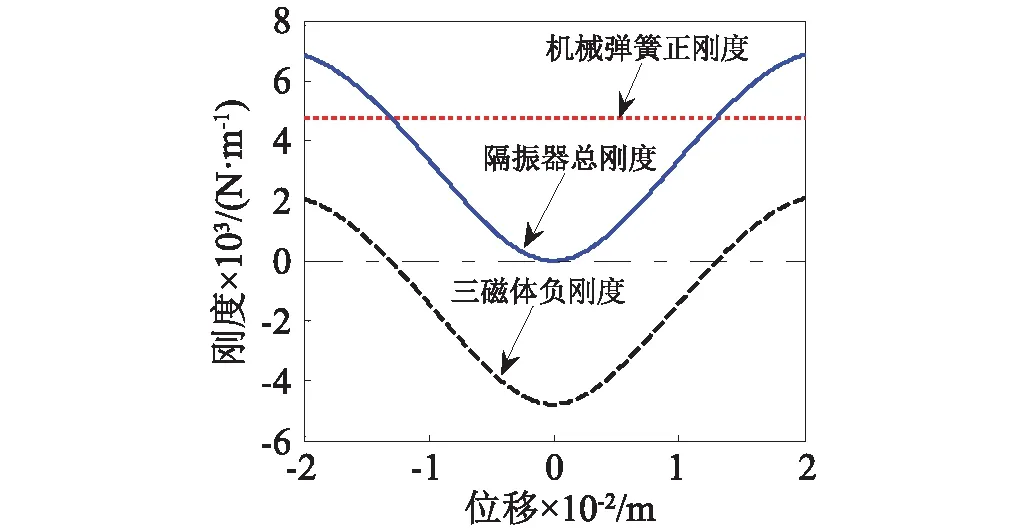
图13 三磁体型隔振器的刚度-位移曲线Fig.13 Stiffness-displacement curve of tri-magnets vibration isolator

具体振动实验步骤如下：

步骤1 调整三磁体型隔振器初始状态。将质量块固定于载物台上，调整调节套使外部磁铁与中间磁铁的中截面重合；

步骤2 将质量块、阻抗头1和激振器通过螺杆连接，阻抗头2和基础固定；

步骤3 将信号源端口与功率放大器相连，完成信号的放大；将功率放大器与激振器相连，完成激振；

步骤4 完成0.5～20 Hz激励频率下的的激振实验，对采集的数据进行相关分析处理；

步骤5 将外部磁铁移除，测量相应的线性系统的隔振性能来进行对比实验。

图14为三磁体型隔振系统与线性系统的力传递率的实验结果对比。由图可知：线性系统在5 Hz附近出现共振峰，从7.5 Hz左右开始有隔振效果；三磁体型隔振系统在0.5 Hz就有隔振效果，0.5～5.5 Hz内力传递率逐渐递减，在5.5 Hz以后，基本保持不变；在13.5 Hz以后，三磁体型隔振系统与线性系统的隔振性能几乎相当。综上所述可知，三磁体型隔振系统相比线性系统具有更低的隔振起始频率和更大衰减率。

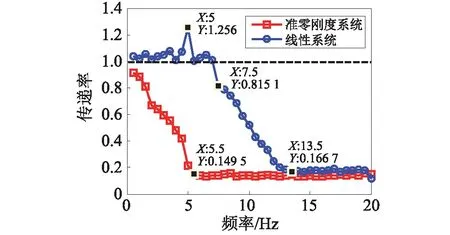
图14 三磁体型系统与线性系统传递率的比较Fig.14 Experimental comparison of force transmissibility between tri-magnets system and linear system

5 结 论

本文通过矩形磁铁与机械弹簧并联设计了一种三磁体型低频隔振器：

(1)利用磁极化强度与磁偶极子之间的关系，计算出单位长度两块磁体之间的静磁能，通过对静磁能求导得到了两磁体间磁力和刚度。

(2)采用矩形磁铁作为负刚度元件，通过合理选择磁铁布置方式和充磁方向，可使其负刚度区间范围扩大，且在区间内刚度变化平缓。

(3)将中间磁铁负刚度作为对象，对三磁体的尺寸参数进行了优化，并通过有限元分析验证了解析模型的准确性。

(4)通过仿真和实验验证，三磁体型低频隔振器具有高静低动的刚度特性，能有效解决低动刚度和失稳的矛盾，为进一步提升潜艇机械设备振动的隔离效果提供了一种新的思路。

[ 1 ] 苏强，王桂波，朱鹏飞，等．国外潜艇声隐身前沿技术发展综述[J]．舰船科学与技术， 2014， 36(1)： 1-8．

SU Qiang, WANG Guibo, ZHU Pengfei, et al. Summarize of foreign submarine acoustic stealth frontier technologies development [J]. Ship Science and Technology, 2014, 36(1): 1-8.

[ 2 ] CARRELLA Z, BRENNAN M J, WATERS T P. Static analysis of a passive vibration isolator with quasi-zero-stiffness characteristic [J]. Journal of Sound and Vibration, 2007, 301: 678-689.

[ 3 ] ORIVUORI J, ZAZAS I, DALEY S, et al. Active control of frequency varying disturbances in a diesel engine [J]. Control Engineering Practice, 2012, 20(11): 1206- 1219.

[ 4 ] 徐道临，张月英，周加喜．一种准零刚度隔振器的特性分析与实验研究[J]．振动与冲击，2014，33(11)： 208-213．

XU Daolin, ZHANG Yueying, ZHOU Jiaxi. Characteristic analysis and experimental investigation for vibration isolator with quasi-zero stiffness [J]. Journal of Vibration and Shock, 2014, 33(11): 208- 213.

[ 5 ] 闫振华，王国强，苏丽达，等．非线性被动隔振刚度特性研究[J]．振动与冲击，2013，32(19)：139-143．

YAN Zhenhua, WANG Guoqiang, SU Lida, et al. Stiffness characteristics of a non-linear passive vibration isolator [J]. Journal of Vibration and Shock, 2013, 32(19): 139-143.

[ 6 ] 王毅，徐道临，周加喜. 滚球型准零刚度隔振器的特性分析[J]. 振动与冲击，2015，34(4)：142-147.

WANG Yi, XU Daolin, ZHOU Jiaxi. Characteristic analysis of a ball-type isolator with quasi-zero-sitffness [J]. Journal of Vibration and Shock, 2015, 34(4): 142-147.

[ 7 ] ZHOU N, LIU K. A tunable high-static-low-dynamic stiffness vibration isolator [J]. Journal of Sound and Vibration, 2010, 329: 1254-1273.

[ 8 ] LI Qiang, ZHU Yu, XU Dengfeng, et al. A negative stiffness vibration isolator using magnetic spring combined with rubber membrane [J]. Journal of Mechanical Science and Technology, 2013, 27(3): 813-824.

[ 9 ] ZHU T, CAZZOLATO B， ROBERTSON W S P, et al. Vibration isolation using six degree-of-freedom quasi-zero-stiffness magnetic levitation[J]. Journal of Sound and Vibration, 2015, 358: 48-73.

[10] SHAN Yuhu, WU Wenjiang, CHEN Xuedong. Design of a miniaturized pneumatic vibration isolator with high-static-low-dynamic stiffness [J]. Journal of Vibration and Acoustics, 2015, 137(4): 1-8.

[11] ZHENG Yisheng, ZHANG Xinong, LUO Yajun, et al. Design and experiment of a high-static-low-dynamic stiffness isolator using a negative stiffness magnetic spring [J]. Journal of Sound and Vibration, 2016, 360: 31-52.

[12] XU Daolin, YU Qiping, ZHOU Jiaxi, et al. Theoretical and experiment analyses of a nonlinear magnetic vibration isolator with quasi-zero-stiffness character- istic [J]. Journal of Sound and Vibration, 2013, 332: 3377-3389.

[13] ROBERTSON W, CAZZOLATO B, ZANDER A. Theoretical analysis of a non-contact spring with inclined permanent magnets for load-independent resonance frequency [J]. Journal of Sound and Vibration, 2012, 331: 1331-1341.

[14] BISWA B. A magnetic quadrupole from rectangular permanent magnets [J]. Nuclear Instruments and Methods in Physics Research A, 2009, 605(3): 233-242.

[15] WU Wenjiang, CHEN Xuedong, SHAN Yuhu. Analysis and experiment of a vibration isolator using a novel magnetic spring with negative stiffness[J]. Journal of Sound and Vibration, 2014, 333: 2958-2970.