一种基于SFS的视乳头三维形貌重建方法
2018-03-28王培培孙九爱
王培培 孙九爱
1(上海理工大学医疗器械与食品学院,上海 200093) 2(上海健康医学院医学影像学院,上海 201318)
引言
青光眼是世界上致盲率第二大的眼科疾病,到2010年为止世界范围内大约有6 000万青光眼患者,到2020年其患病数量预计将会继续增加2 000万[1]。青光眼疾病的发生是由于眼底视神经细胞损伤造成眼底视盘和视杯几何形状的改变。视盘也称视乳头位于视网膜的远端部分,是视神经纤维和血管进出眼球的入口,正常情况下由于视神经纤维穿过呈现粉红色。视杯是视盘内部无视神经纤维通过的部分,呈现苍白色。青光眼的主要发病机制为:眼内压升高,筛板受到挤压导致视神经损伤,从而导致视杯变大[2-4]。随着病程的加长,会出现视觉损伤,甚至是造成不可逆转的失明[5]。在临床上,一般是通过计算视杯和视盘的垂直距离比来对青光眼进行诊断[6]。因此,视盘、视杯形态结构的准确分割和测量对青光眼的诊断是很重要的[7-8]。
目前,在临床上青光眼的诊断有两种方式。第一种方式,医生依据眼底照相机拍摄的二维图像进行判断,这需要依靠临床医生的行医经验,判断结果存在一定的主观性。第二种方式,为了提高诊断精度,同时出现了三维成像设备,如光学相干断层成像(OCT)[9-10]和海德堡视网膜断层扫描仪(HRT)[11-12],这可以通过得到眼底的三维图像对眼底疾病进行诊断。但是,这两种方式在使用之前都需要对操作人员进行专业的培训,价格昂贵而且耗时较长[13]。
目前通过眼底照片直接进行三维重建的国内外的文献数量很少,而且局限性较强。Enrique等主要研究的是眼底局部的三维重建[14],存在一定的局限性。陈骥等分析了正常眼和屈光异常眼眼底图像的关系,建立了从二维平面图像到三维曲面图像的映射关系来对眼底图像进行三维重建[15]。李超等则是把眼底二维图像反投影到三维球面上以实现眼底图像的三维重建[16]。但他们所采用的三维眼底重建方法建立的眼底三维曲面只能描述眼底的总体表面情况,并不能提供更多的三维细节信息。
为此,本研究提出了一种眼底图像三维重建的新方法即从明暗恢复形状法(shape from shading,SFS)[17]。其主要思想是,根据眼底数字照相机拍摄的二维眼底数字图像的灰度值变化恢复出眼底三维结构形貌。初步实验结果表明,该方法可行性较强,能够提供更多的线索辅助临床医生对青光眼等眼底类疾病进行诊断。
2 方法
2.1 算法实现流程
本算法的实现主要有以下步骤,如图1所示。第1步,使用数字眼底照相机拍摄眼底图像;第2步,对图像进行预处理,包括把RGB图像转化为灰度图像,进行图像分割、滤波和白平衡处理;第三步,计算估计眼底照相机拍摄眼底图像的光源方向;第4步,利用Tsai[18]线性化方法分析求解SFS算法,再结合第3步求出的光源方向,对眼底图像进行三维重建;第5步,可视化重建后的视乳头三维结构形貌图。

图1 视乳头三维重建流程Fig.1 Diagram of reconstructing 3D topographic map of the ONH
2.2 从明暗恢复形状法
20世纪70年代,Horn提出了一种恢复物体表面三维形貌的新方法——从明暗恢复形状法(SFS)[19]。其主要原理是:假设物体的表面反射模型为朗伯体表面反射模型,计算出图像表面的光源方向;再根据二维图像的明暗(亮度值)变化,经过一定的算法,计算出每一点的高度值,恢复出物体的三维形貌。
一般情况下,当光照射到物体表面时,其表面会同时发生漫反射和镜面反射。朗伯体表面反射模型是一种理想的情况,其假设物体表面只有漫反射,没有镜面反射,即物体表面的亮度不会随观察角度的改变而改变。在使用SFS算法恢复出物体三维形貌的过程中,需要同时假设物体表面是光滑的,即其表面函数具有一阶连续导数。
SFS是一种病态问题的逆运算算法,为解决病态问题,其算法也经过了一系列的改进,出现了演化法、最小值法、局部分析法和线性化法。考虑到实现的效率因素,本研究采用线性化法对SFS算法进行求解,进而实现了眼底视乳头的三维重建。
2.2.1计算与估计视乳头光照方向
相比较眼底图像,视乳头是一个较小的区域。视乳头中粉红色的部分是血管和视神经进入视网膜的一个切入点(视盘),视盘中没有视神经穿过且呈现灰白色的部分是视杯。在眼底图像拍摄的过程中,通常以黄斑作为眼底摄影的中心,而视乳头偏向于鼻侧,因此不能简单地把视乳头摄影视为一个同轴眼底光学系统。所以,在使用SFS方法对视乳头进行三维重建时,需要预先估计出光照方向[20]。

图2 反射模型Fig.2 Surface reflection model
图2所示为视乳头的表面反射模型。以二维图像上的某一点为例,建立直角坐标系,其中z轴表示物体的高度方向,x轴的值表示图像上某一点像素点的行数,y轴的值代表图像上某一点像素点的列数。假设α角为x轴与表面法向量在xy平面的投影的夹角,β表示z轴与表面法向量的夹角,τ表示光源方向在xy平面的投影与x轴的夹角,σ表示光源方向与z轴的夹角。其中,α,τ∈(0,2π),β,σ∈(0,π/2)。
根据笛卡尔坐标系和球面坐标系的关系,视乳头的表面法向量,光源方向和辐射方程可以分别表示为
n=[sinβcosα,sinβsinα,cosβ]T
(1)
I=[sinσcosτ,sinσsinτ,cosσ]T
(2)
E(α,β)=(sinβcosαsinσcosτ,
sinβcosαsinσsinτ,cosβcosσ)
(3)
β与cosβ呈线性变化,α服从均匀分布。σ和τ可以通过对亮度方程和亮度的平方方程求解积分得到,即
f(α,β)=cosβ/2π
(4)
式中,μ1和μ2分别表示所给图像的亮度值和亮度值的平方。
利用式(5)、(6)可求出σ和τ的表达式,有
(7)
(8)
利用式(7)、(8)即可求出其角度值,把其角度值代入式(2)中,即可得到光源方向。
2.2.2SFS算法实现
假设视乳头区域表面的反射模型为朗伯体反射模型,则图像的亮度方程为
(9)
或
(10)
其中,令I=(n01,n02,n03)和I=(-p0,-q0,1)表示光源方向,两者的关系为
(11)
(p,q)为图像上任意一点的梯度值,任意一点的高度值为z=z(x,y),表面法向量为n=(n1,n2,n3)。高度值和梯度值之间的关系为p=∂z/∂x,q=∂z/∂y。表面法向量和梯度值是使用SFS算法进行三维重建的两个重要的参数值。假设一幅图像有M×N个像素值,根据SFS算法其有M×N个方程,但是却有2×M×N个待求量。为解决这个问题,本研究采用Tsai的离散线性化方法对方程进行求解。
根据Tsai的离散化原理,令z(i,j)表示图像上第(i,j)点的高度值,则图像的表面梯度可以表示为
(12)
假设一幅图像的行数和列数分别为M、N,则i和j的取值范围为:i=0, 1, 2,…,M-1;j=0, 1, 2,…,N-1。则亮度方程的差分方程为
(13)
再利用泰勒公式改写式(13),得到
(14)
(15)
其中
(16)

3 实验结果
为得到局部视杯图像,本研究对RIM-ONE眼底图像数据库的图像[21](包含正常眼和疑似青光眼图像)进行预处理,利用自动阈值分割和区域生长法对眼底图像进行分割,得到了如图3所示的包含视杯的局部眼底图像。

图3 眼底RGB图像。(a)和(b)是正常眼底视杯图像;(c)和(d)是疑似青光眼患者眼底图像Fig.3 The RGB fundus image.(a)and (b) are normal fundus images; (c) and (d) are suspicious glaucoma fundus images
利用Matlab软件对图像进行白平衡处理,消除光线对图像的影响,然后把RGB图像转化为灰度图像,接着利用图像的亮度(灰度值信息)求出每幅视乳头图像的光源方向。通过对式(5)、(6)进行求解,计算出4幅图像的光源方向为
Ia=(0.543 1,-0.023 9,0.839 3)
Ib=(0.339 6,0.523 8,0.839 3)
Ic=(0.566 7,-0.266 1,0.792 3)
Id=(0.616 9,-0.030 3,0.786 4)。
然后,利用上述所求的光源方向结合SFS算法,对图像的每一个像素点的灰度值进行处理,得到图像三维数据,对眼底表面形貌进行三维重建,即可得到如图4所示的重建后的视乳头三维形貌图。
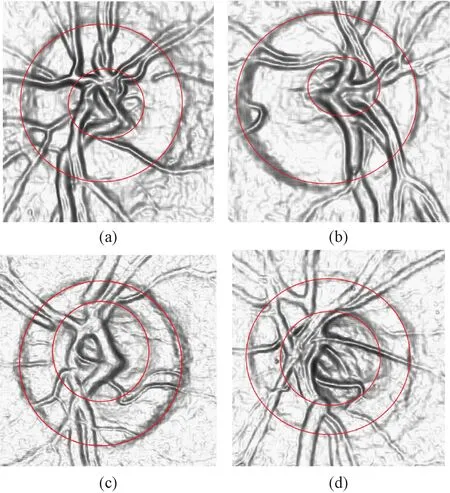
图4 重建后的三维眼底图。(a)和(b)是正常眼底视杯图像;(c)和(d)是疑似青光眼患者眼底图像Fig.4 Reconstructed three dimensional fundus image.(a)and (b) The normal fundus images; (c) and (d) The suspicious glaucoma fundus image
在图4中,(a)和(b)是正常眼底图像的视杯图形,(c)和(d)是青光眼患者的眼底图像。从图4中可以很清晰地分辨出(c)和(d)两幅青光眼眼底形貌图中视盘和视杯的边界信息。计算每幅眼底图像中视盘和视杯的垂直直径比可得出,图4中的眼底图像(a)~(d)的杯盘比比值分别为0.46、0.35、0.611、0.614。由此亦可判断出,图4中的前两幅图像为正常眼的视乳头三维重建结果,后两幅为青光眼患者的视乳头三维形貌图。此结果与事实相符合。
因此,视乳头形貌的三维重建,可以更加方便、准确地计算视杯和视盘的比值,对青光眼地诊断和辅助治疗提供帮助。
4 讨论和结论
本研究主要提出了一种获取眼底结构三维形貌的方法,为眼底疾病的诊断和跟踪治疗提供一种简单、经济方便的手段。而且,从图4的三维重建结果可以看出,利用SFS算法对眼底局部图像进行三维重建的效果较好,能够很清晰地提供视盘和视杯的边界信息,更加准确地计算出视杯和视盘比值,为青光眼的诊断和跟踪治疗提供更加有效便利的方式。
在本研究中,利用阈值分割和区域生长法,对数字眼底照相机获得的眼底图像进行分割,得到视乳头区域图像,如图3所示。再利用白平衡消除光线影响,然后经图像滤波和灰度变换得到眼底灰度图像。接着利用图像亮度方程和亮度值得到视乳头图像光源方向。但是,使用此方法虽能得到眼底图像的光源方向,但其结果受到图像预处理的影响。最后利用SFS算法计算得出视乳头图像的三维高度值如图4中的图像所示。
临床上,当视杯视盘的比值大于等于0.6时[6],即可诊断为青光眼。从本研究的实验结果中得出的视乳头中视杯和视盘的比值可以发现,利用本研究的算法得出的青光眼患者的视乳头三维重建形貌图形中的杯盘比大于0.6,正常眼的杯盘比小于0.6,与临床上的诊断结果相吻合。因此,本算法系统可以辅助青光眼的诊断。
但是,目前的研究只对与青光眼有关的视盘部分进行了三维重建。下一步将扩展算法,以便能够对完整眼底图像进行重建,为更多眼底疾病的诊断和跟踪治疗提供可能。
[1] Quigley HA, Broman AT. The number of people with glaucoma worldwide in 2010 and 2020 [J]. Digest of the World Core Medical Journals, 2006,90(3):262-267.
[2] 党鸿, 辛晓蓉. 青光眼视神经损伤机制的研究进展 [J]. 眼科新进展, 2016, 36(7):680-683.
[3] Septiarini A, Harjoko A. Automatic glaucoma detection based on the type of features used: A review [J]. Journal of Theoretical & Applied Information Technology, 2015,2872(3): 366-375.
[4] Kilintzis V, Chouvarda I, Topouzis F, et al. Symbolic representation of optic nerve head cup presents difference in patients with Primary Open Angle Glaucoma[C]// IEEE International Conference on Information Technology and Applications in Biomedicine. Corfu:IEEE, 2011:1-4.
[5] Heijl A, Aspberg J, Bengtsson B. The effect of different criteria on the number of patients blind from open-angle glaucoma[J]. BMC Ophthalmology, 2011, 11(1):1-6.
[6] Almazroa A, Burman R, Raahemifar K, et al. Optic disc and optic cup segmentation methodologies for glaucoma image detection: A survey [J]. Journal of Ophthalmology, 2015, 2015(7):1-28
[7] Mary MCVS, Rajsingh EB, Jacob JKK, et al. An empirical study on optic disc segmentation using an active contour model [J]. Biomedical Signal Processing & Control, 2015, 18:19-29.
[8] Nawaldgi S. Review of automated glaucoma detection techniques [C]//International Conference on Wireless Communications. Signal Processing and Networking. Boston:IEEE, 2016:1435-1438.
[9] Huang D, Swanson EA, Lin CP et al. Optical coherence tomography[J]. Science, 1991,254(5035):1178-1181.
[10] 郭慧敏. OCT检测视网膜神经纤维层厚度在青光眼诊断中的应用进展 [J]. 医学综述, 2013, 19(7):1281-1283.
[11] Kamal DS,Garwayheath DF,Hitchings RA,et al. Use of sequential Heidelberg retina tomograph images to identify changes at the optic disc in ocular hypertensive patients at risk of developing glaucoma[J]. British Journal of Ophthalmology, 2000,84 (9): 993-998.
[12] 邢业娇, 王大博, 纪珍,等. 海德堡OCT测量后极部视网膜厚度对青光眼诊断价值 [J]. 青岛大学医学院学报.2013, 2013(1):38-40.
[13] Yin F, Wong DWK, Quan Y, Ai PY, Tan NM, Gopalakrishnan K, et al. A cloud-based system for automatic glaucoma screening [C]//Annual International Coference of the IEEE. Milan:IEEE, 2015: 1596-1599.
[14] Corona E, Mitra S, Wilson M, et al. Digital stereo image analyzer for generating automated 3-D measures of optic disc deformation in glaucoma[J]. IEEE Transactions on Medical Imaging, 2002, 21 (10): 1244-1253.
[15] 陈骥, 彭承琳. 眼底图像的三维重建[J]. 生物医学工程杂志, 2008,25(1):177-181.
[16] 李超, 梁斌, 陈武凡, 等. 由二维眼底正投影图像向三维曲面逆投影成像的重建算法[J]. 中国生物医学工程学报, 2002,21(4):346-350.
[17] Horn BKP. Height and gradient from shading[J]. International Journal of Computer Vision, 1990,5(1):37-75.
[18] Tsai PS, Shah M, editors. A fast linear shape from shading [C]// Proceedings 1992 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Champaign:IEEE, 1992:734-736.
[19] Horn BKP. Shape from Shading: A Method for Obtaining the Shape of a Smooth Opaque Object from One View[M]. Cambridge: MIT Press,1970.
[20] Elhabian SY. Hands on shape from shading [J]. Technical Report, 2008.
[21] Fumero F, Alayon S, Sanchez JL, et al. RIM-ONE: An open retinal image database for optic nerve evaluation[C]// Proceedings of the 2011 24th International Symposium on Computer-Based Medical Systems. Washington DC: IEEE, 2011:1-6.
