梯度风观测资料在高层建筑气象灾害风险评估中的应用研究

鞠红霞，刘素萍，何 芍

(泰州市气象局 江苏泰州225300)

0 引 言

随着国民经济的迅速发展，高层建筑如雨后春笋般崛起，特别是出现了不少综合性的高层建筑。风是影响高层建筑物设计的主要气象因素之一，兴建一座有足够抗风强度的高层建筑需要提供不同重现期的最大风速值。由于各地气候背景的差异，加之近地层风受地理和地表状况的影响很大，单纯依靠邻近气象站观测资料直接推算高层建筑物的抗风参数，或者利用粗分辨率的全国风压图通过内插反推高层建筑物的抗风参数，都不能较为准确地反映实际风的特征，达不到高层建筑的抗风设计要求。因此，在气象灾害风险评估中，结合气象站多年风观测资料，正确分析地区梯度风观测资料，估算出地区高层建筑多年一遇的极大风速值，作为设计部门设计抗风参数时的重要依据，对提高高层建筑气象灾害防御的能力显得尤为重要[1]。

本文利用泰州气象站年最大风速资料和梯度风观测资料，应用耿贝尔极值Ⅰ型分布，系统分析计算得到本地区高层建筑若干年后不同重现期最大风速极值，应用到高层建筑气象灾害风险评估报告中，为高层建筑抗风设计提供了科学的气象参数。

1 数据来源与评估方法

1.1 数据来源

泰州斜桥气象观测站 1966—2003年连续 38年的最大风速观测资料用于计算本地区10,m高度处不同重现期的最大风速极值。

泰州梯度风自动观测系统2007年8月份建成投入使用，用于观测近地面不同高度风速、风向数据。梯度风观测系统安装于总高 218,m的钢结构电视塔上，在塔的 35,m、85,m、135,m 3个平台上各安装2套风传感器，取得了2007年10月～2012年12月期间逐日的不同高度处风观测资料。

1.2 方法

1.2.1 耿贝尔极值Ⅰ型分布

根据高层建筑抗风参数的设计要求[2]，需要以极端的气候状态作为设计条件，因为气象记录中的极大风速值是观测时期内的极大值，只有相对意义，高层建筑可能遇到的极端风速不能简单地用气象记录中的极值计算，而需要利用最大风速的概率分布来推算出百年一遇的最大风速。

所谓极值分布就是在n个观测值中极大值或极小值的概率分布。

设X为随机变量，X1，X2，…Xn为X的样本，如将样本从小到大排列成：

则Xn*就是样本(X1，X2，…Xn)的极大项，而X1*就是样本(X1，X2，…Xn。)的极小项，极值分布就是代表Xn*或X1*这样的随机变量的分布。由于n的变化，求Xn*、X1*的分布，实质上是一种极限分布或渐近分布。

它的概率密度函数和保证率分布函数[3]分别为：

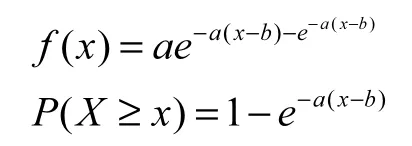
由耿贝尔方法[4]：

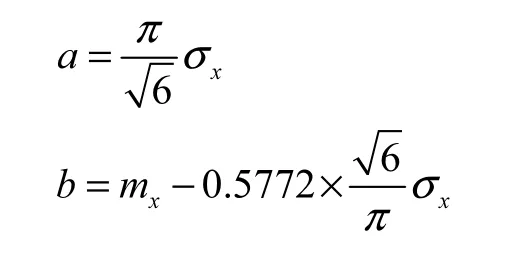
这里mx、xσ分别为样本的数学期望和均方差。根据上述分布函数，对于给定的保证率p所对应的xp，由：

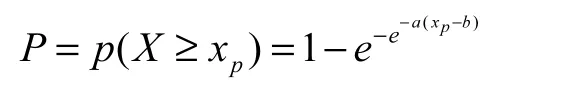
解得：

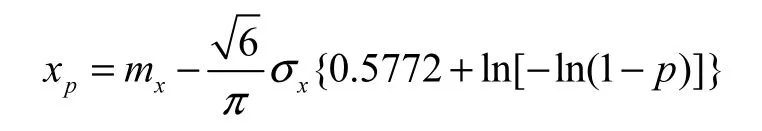
1.2.2 风廓线指数计算方法

在 500～1,500,m 以下的大气摩擦层中，风随高度的变化，最常用的模拟规律为指数律。根据现行《建筑结构荷载规范》及《公路桥梁抗风设计指南》所推荐的风随高度变化规律相一致，近地层风随高度变化的指数公式为：

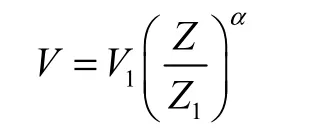
式中：V为高度Z处的风速，V1为已知高度Z1处的已知风速，α为风廓线指数。

1.2.3 移动t检验法

移动 t检验法可进行均值差异性检验[5]，方法如下：

计算统计量：

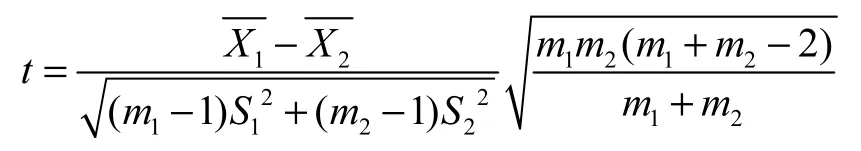
2 结果与分析

2.1 气象站年最大风速序列的均一性审查与处理

《建筑物结构荷载规范》(GB 50009—2012)规定：推算多年一遇的最大风速时，所用的风速资料为开阔地面10,m高度处的10,min平均最大风速。在计算中，风速资料序列主要选取气象台站建站以来自记10,min平均最大风速为统计样本，在概率计算之前对代表性、准确性和连续性进行审查、处理。

对泰州气象观测站1960年以来观测的平均风速(2,min)的年值序列进行均一性分析[6]，1965年维尔达测风器改为电接风向风速计(自记 10,min平均风速观测)，1978年气象观测站由泰州市东郊斜桥迁至东郊斜桥南，2004年由人工观测站调整为自动气象观测站，且泰州站 2005—2006年的数据为空值。应用移动t检验方法(显著性水平 0.05)进行两个时间点前后时段的显著性检验，如检验结果显著，则认为该点是不连续点。检验主要为 1965年和 1978年的假设断点，1965年仪器更换造成风速资料不连续，1978年的台站迁移对风速无影响。因此选取 1966—2003年的年最大风速序列资料来进行计算，图 1为泰州市斜桥气象站1966—2003年逐年最大风速变化图。从图中可以看出，最大值为20.3,m/s。

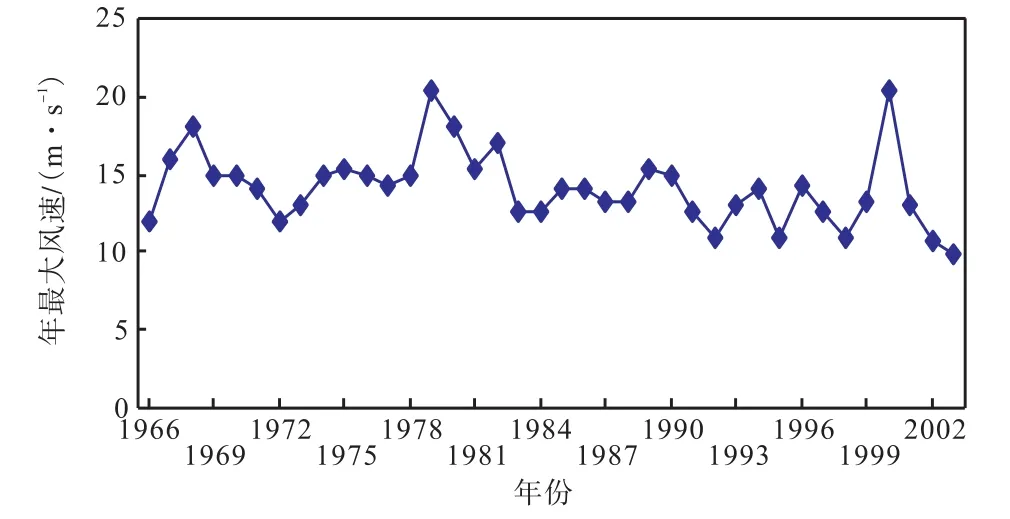
图1 泰州斜桥气象站年最大风速变化图Fig.1 Annual maximum wind speed variation measured by Taizhou Xieqiao meteorological station

2.2 气象站年最大风速的概率计算

在高层建筑的气象灾害风险评估中，对风压的评估尤其重要，选择恰当就会产生巨大的经济效益。根据高层建筑抗风参数的设计要求，首先要弄清当地风的极端气候状态，以及十年一遇、百年一遇的概率。

拟合极值分布的方法有多种，气象上常用如P-Ⅲ型和极值Ⅰ型[7]等，研究表明它们与气象要素极值分布拟合良好，在气象、水文上获得广泛的应用。根据泰州斜桥气象站1966—2003年的最大风速资料，用耿贝尔极值Ⅰ型分布对泰州市年最大风速进行拟合，进而计算泰州斜桥气象站10,m高度处不同重现期下的10,min平均年最大风速，结果见表1。

表1 泰州斜桥气象站不同重现期的基本风速Tab.1 Basic wind speeds at different return periods measured by Taizhou Xieqiao meteorological station

对上述结果做柯尔莫哥洛夫方法进行拟合优度检验，样本理论分布函数与经验分布最大的离差Dn＝0.089,1，Dn＜D0.05＝0.215。因此，耿贝尔分布函数计算重现期其拟合优度满足要求。

2.3 梯度风观测资料在气象灾害风险评估中的应用

2.3.1 梯度风观测资料的分析和处理

2007年1月1日，新建泰州气象观测站，位于泰州市西郊乡森北村，风速仪的安装高度为10,m。利用2007年10月～2012年12月期间逐日的梯度风不同高度观测资料及泰州森北气象观测站同期10,m高度处风观测资料，用于风廓线指数的计算。从图 2选取的部分梯度风观测站和森北气象观测站同期风观测资料分析图可以看出，风速随着高度的增加明显增大。

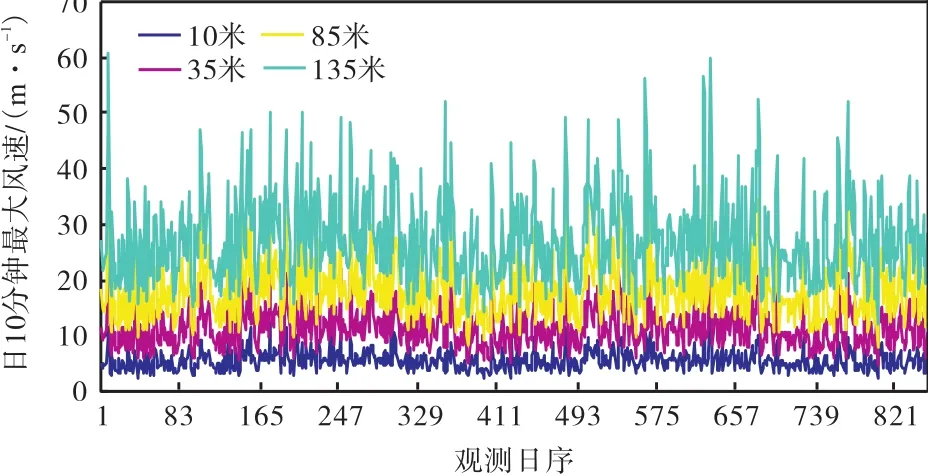
图2 梯度风观测资料和森北气象观测站同期风观测资料对比图Fig.2 Comparison of gradient wind observation data with the wind observation data measured by Senbei meteorological observation station at the same time

2.3.2 高层建筑各高度设计风速的推算

《建筑结构荷载规范》中要求，在推算50年一遇的最大风速时，根据提供的风廓线指数取值，不同地面粗糙度对应不同α值，见表2。

表2 各种地面粗糙度条件下的风廓线指数Tab.2 Wind profile indices under various surface roughness conditions

根据 2007年10月～2012年 12月梯度风观测资料和森北气象观测站同期风观测资料，35,m和10,m处风速资料，利用风廓线指数计算公式进行拟合，得出α为 0.12；85,m和 10,m处风速资料拟合出α为 0.13；135,m和 10,m处风速资料拟合出α为0.20，符合地面对风的摩擦阻力随着离地面高度的增加而减小，从而使风速随高度的增加而变大的规律。根据《建筑结构荷载规范》中的地面粗糙度分类，泰州地区可归为 C类，α值与 135,m处实测值比较接近。泰州地区高层建筑一般不高于 150,m，结合计算出的α值，α取值为0.22，根据表1利用风廓线指数计算方法推算出离地面120,m以内每10,m高度层不同重现期最大风速值，结果见表3。

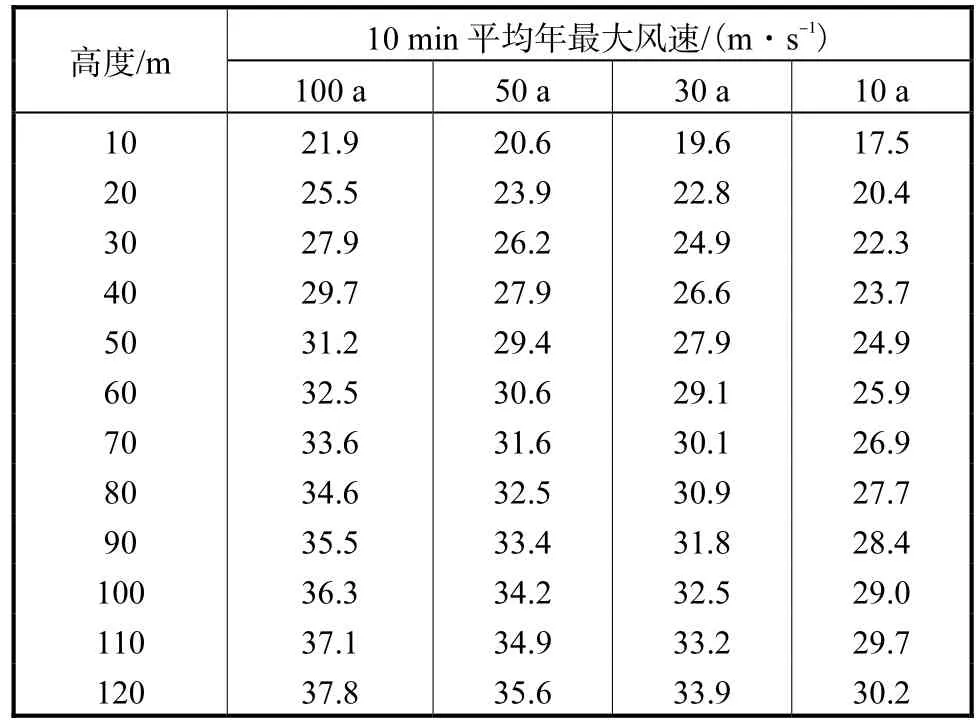
表3 泰州地区不同高度不同重现期 10,min平均年最大风速Tab.3 10,min average annual maximum wind speeds at different heights and different recurrence intervals in Taizhou area

从表3可以看出，随着高度的增加，10,min平均年最大风速也明显增大，120,m处风速明显大于10,m处风速。

2.3.3 与风压荷载计算法反推高层建筑的设计风速比较分析

查询《全国基本风压分布图》，得设计频率为10,a、50,a和 100,a一遇时泰州地区相应的风压值分别为 0.25,kN/m2、0.4,kN/m2和 0.45,kN/m2，根据风压荷载计算公式推算出离地10,m高度处10,a、50,a和100,a一遇10,min平均年最大风速取值分别为 20.0,m/s、25.3,m/s 和 26.8,m/s，10,a、50,a 和100,a的规范所取基本风速比表3中对应的计算值分别偏大 2.5,m/s、4.7,m/s和 4.9,m/s。

计算结果和表3比较可以看出，《全国基本风压分布图》在计算泰州地区风压时使用的基本风速取值明显偏大，而且随着设计年限的增加，差值也呈增大趋势，使用规范给出的风压值会造成投资太大而浪费资金。因此将梯度风观测资料应用于高层建筑气象灾害风险评估报告，意义十分重大。

3 结 论

采用泰州斜桥气象站 1966—2003年共 38年最大风速资料序列，利用耿贝尔极值Ⅰ型分布函数，计算得出了泰州地区不同重现期(100,a、50,a、30,a、10,a)10,m高度处 10,min平均年最大风速分别为21.9,m/s、20.6,m/s、19.6,m/s、17.5,m/s。

结合泰州电视塔35,m、85,m和135,m高度的同步梯度风观测资料，计算得出了泰州地区风廓线指数，从而可推算出不同高度、不同重现期(100,a、50,a、30,a、10,a)的最大风速极值。

根据《全国基本风压分布图》反推出泰州地区10,m高度处基本风速取值与计算值相比明显偏大。因而，在气象灾害风险评估中应用梯度风观测资料来进行不同高度基本风速的计算，能为本地区高层建筑抗风设计提供科学经济的气象参数。

［1］全涌，姚博，顾明. 高层建筑结构抗风可靠性研究进展[J]. 同济大学学报：自然科学版，2015，43(6)：807-815.

［2］中华人民共和国住房和城乡建设部. 建筑结构荷载规范：GB,50009—2012[S]. 北京：北京中国建筑工业出版社，2012.

［3］王海军. 城市暴雨强度公式推求软件系统设计[D]. 武汉：华中科技大学，2005.

［4］任丽伟，王辛方，李喜平，等. 鹤壁市单日降水量极值估算[J]. 气象与环境科学，2009，32(2)：46-49.

［5］杨宏青，陈正洪，高雪飞. 鄂东长江公路大桥设计风速推算研究[J]. 气象科学，2010，30(4)：526-529.

［6］刘佳，马振峰，范广洲，等. 多种均一性检验方法比较研究[J]. 气象，2012，38(9)：1121-1128.

［7］马开玉，张耀存，陈星. 现代应用统计学[M]. 北京：气象出版社，2004.