Application of K-means and PCA approaches to estimation of gold grade in Khooni district(central Iran)

Neda Mahvash Mohammadi•Ardeshir Hezarkhani•Abbas Maghsoudi

1 Introduction

Evaluation of ore resources is essential for the economic planning of a mining project(Pham 1997).One of the important parameters of resource evaluation is grade estimation.Grade estimation plays a signi fi cant role in evaluating the economic viability of an ore body.There are various methods to estimate grade,including those based on distance and geostatistics(Hassani Pak and Sharafeddin 2005),and nonparametric estimation(Davis and Jalkanen 1988).Recently,clustering methods have been used extensively in the earth sciences to categorize geochemical data.This approach divides the data into clusters;within each cluster,the similarity between data is maximized,and in different clusters,it is minimized(Berkhin 2006).There are no categories of original data;indeed,variables are not divided into independent and dependent groups.Rather,the approach seeks groups of similar data that can be organized by the behavior of the data to achieve better results(Malyszko and Wierzchon 2007).The clustering method is an indirect method.It can be used without previous information on the internal database structure and can illuminate hidden patterns and promote the performance of direct methods(Abolhassani and Salt 2005).K-means is one of the most important and ef fi cient clustering methods and is widely used for data classi fi cation(Lloyd 1957;MacQueen 1967;Hartigan and Wong 1979).K-means clustering allocates all data to k classes.Data within one class are similar,while data in different classes are dissimilar.Cluster analysis endeavors to minimize the average squared distance between data points.In the beginning,random k clusters are selected,with each observed point deposited in the gravity center of the classes(for example,by applying Euclidean distance).This determines the cluster center.There are many algorithms for k-means,but the algorithms of Hartigan(1975)and Mac Queen(1967)are more common than the others.If Manhattan distance is used,the mean of each cluster could double as the gravity center.Algorithm results depend on the number of initial clusters.Therefore,it is possible to choose the appropriate results by using different initial k(Templ et al.2008).Sometimes,principal component analysis(PCA)is used before cluster analysis in order to reduce the dimensionality of the data set(Ng et al.2001;Yeung and Ruzzo 2001;Zha et al.2001).Ding and He(2004)presented the relationship between k-means and PCA.They also showed that principal components are the ongoing solutions to the discrete cluster membership indicators for k-means clustering(Ding and He 2004).Consequently,new lower bounds are achieved for the k-means function.

Multivariate statistics allows the discovery of geochemical patterns of elements and the investigation of several variables simultaneously.This method is more frequently used in earth sciences due to its greater reliability over univariate and bivariate statistical methods(Howarth and Sinding-Larson 1983).The method’s numerous applications include:determining geochemical anomalies(Loska and Wiechuła 2003),remote sensing studies(Loughlin 1991;Crosta and Rabelo 1993;Du and Flower 2008),environmental studies(Loska and Wiechuła 2003),oil and gas studies(Prinzhofer et al.2000;Pasadakis et al.2004),and geophysical studies(Sabeti et al.2007).PCA is one of the multivariate statistical methods based on eigenvalues and eigenvectors.PCA detects directions with the highest variation and moves the data to a new coordinate system,reducing the dimension of the data set and summarizing the data characteristics(Jolliffe 1986).However,information about the source of the sample is required,a non-trivial task due to the huge number of sources and the complexity of in-ground networks.The useful and popular methods of PCA and clustering make use of data source analysis.

In this paper,PCA was applied for clustering and reducing the dimension of original data and then k-means was used to investigate the behavior of identified elements.This process allowed for the estimation of gold ore grade.

2 Geology of the Khooni district

Anarak is the most important metallogenic province of Iran,hosting numerous ore deposits and mineralized veins in its magmatic and metamorphic upper Proterozoic rocks.Previous studies in this area have identified a variety of metallic and non-metallic deposits,including deposits of lead,zinc,gold,silver,chromite,iron,manganese,molybdenum,antimony,etc.The variety of mines in the area has attracted a number of researchers.Khooni is one of the most famous mines in the east of Anarak.It has been an important source of gold(Mahvash Mohammadi et al.2016).Khooni is 60 km northeast of Anarak and 270 km from Esfahan and belongs to the Central Iran geological zone,one of the most complex structural units of Iran due to its position between the Iran and Turan Plates.Faults in the study area include the Darune in the north,the Dehlim-Baghet in the west,the Bashagard in the south,and the Nahbandan in the east(Darvish 2011).

The first scientific study on the Khooni District was performed by Adib(1972).He carried out multiple atomic absorption analyses to determine the mineralogy.Adib discovered a large amount of gold in the silica and carbonate veins in the study area;the average content of gold was presented as 20 ppm(Adib 1972).The mineralization is mainly vein and poly-metal(Nezampoor and Rasa 2005).Promising mineral potential was signaled by the mineralization and by study of remote sensing maps in the region.According to Mahvash Mohammadi et al.(2016),gold mineralization in the area is at a sufficient grade and tonnage to warrant exploratory investigation.

Active tectonism and faults have played a major role in the tectonic structure,position of veins,position of igneous rocks,alteration,and mineralization in this area(Bagheri et al.2007).Eocene magmatism and tectonism along with multiple phases of metamorphism are collectively responsible for the deposits.

Stratigraphy of the study area is from Precambrian to Quaternary.Outcrops in the western portion of the area mainly consist of Cambrian metamorphic units,while in the east are Eocene volcanics and pyroclastics with a dominant composition of and es ite and trachey andesite cut by monzonite dikes.Outcrops of Cretaceous limestone in the northwest corner of the area unconformably overlie older units.Low altitude and lowland areas are covered by old alluvial terraces,plains sediments,and young alluvial deposits.The oldest lithostratigraphic units in the region are a series of metamorphic rocks including schist,quartzite,marble,and amphibolite with serpentine blocks from Precambrian to lower Cambrian (Fig.1;Heydarian Dehkordi and Rassa 2011,2012).

3 Principal component analysis

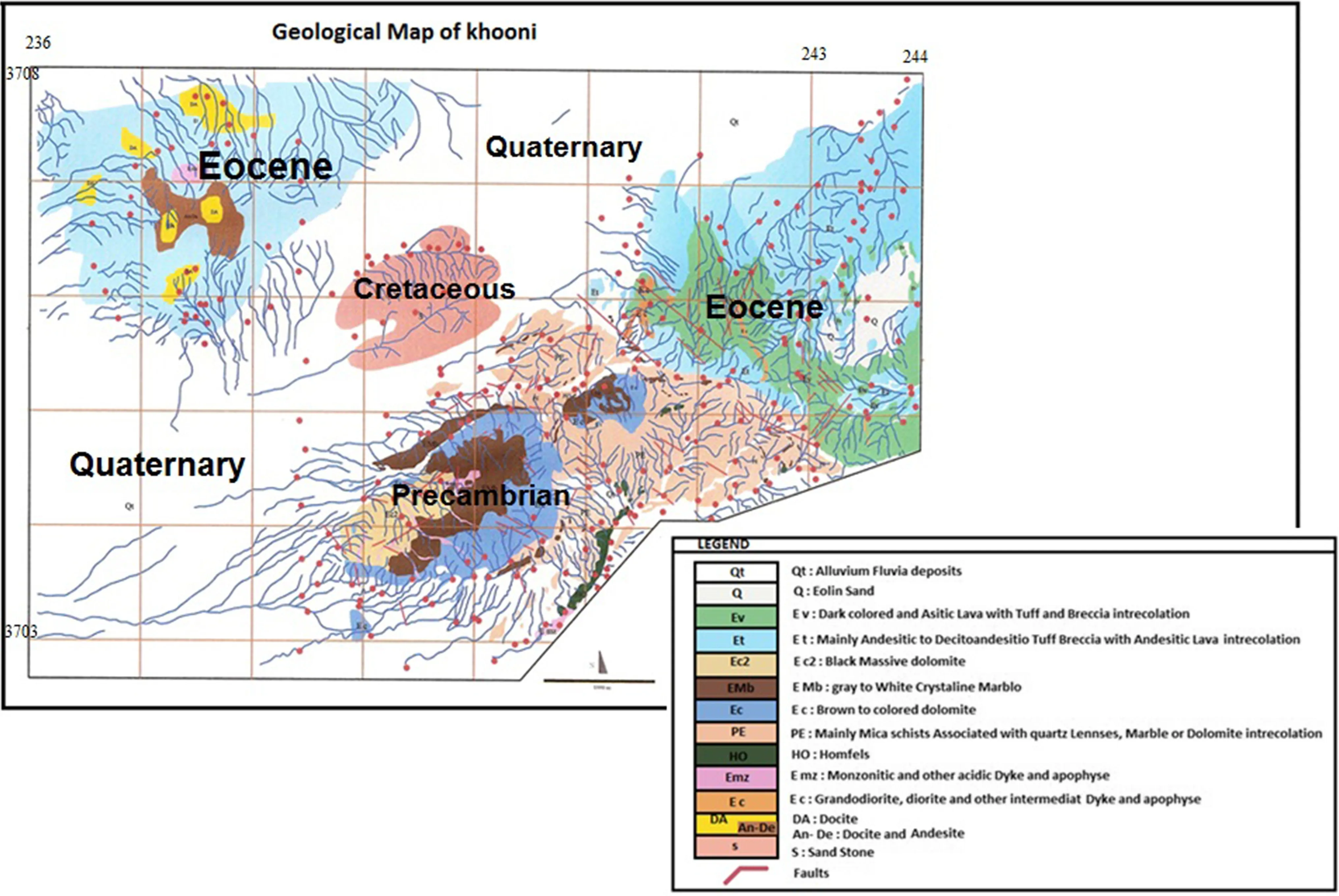
Fig.1 Geological map of Khooni district(Pourjabar 2005)

PCA is one of the most powerful multivariate techniques for data analysis and processing(Jolliffe 1986)and is frequently used in data analysis(Lin 2012)across many fields,such as data compression,image processing,visualization,exploratory data analysis,pattern recognition and time series prediction(Tipping and Bishop 1999;Labib and Vemuri 2005).PCA is applied to reduce dimensions and obtain a smaller number of variables for input to further analysis.In order to achieve this,PCA transforms initial data into a new set of variables—the principal components(Jolliffe 2002).The goal of PCA is to summarize the features of the data.For example,PCA was used to reduce and select the features of the reflectance spectra of lunar soil samples(Xiaoya et al.2009).

PCA is based on eigenvalues and eigenvectors(Hotelling 1933).It works by identifying directions with the largest variances,then calculating the principal components,which are linear combinations of the correlated initial variables.The initial variables’N-dimensional space is transformed into new Cartesian coordinates of uncorrelated variables in a P-dimensional space such that P is less than N(P＜N).

As mentioned,PCA is a method for finding linear combinations of the correlated initial variables to make a new coordinate system.The new directions are along the largest variance.The component with the largest variance among all principal components is considered the main(PC1).The second(PC2)has the largest possible inertia,has lower variation than PC1,and is orthogonal to PC1.The other components are computed as well.Assume PC1 is a linear combination X1to Xnof the initial variables(Hassani Pak and Sharafeddin 2005):

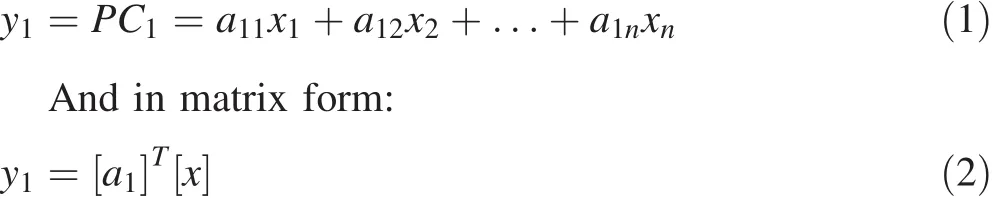
If aijcoefficients(weights)of the linear combination were large,the variance would increase significantly.Therefore,the coefficients are limited as follows:

where[S]is the original variables’covariance matrix and aijare the initial variables’coefficients.The main component can be indicated as a vector[Y],the total of initial variables as another vector[X],and their weights in the form of a matrix[A],with the relationship expressed as follows:

The number of computable principal components depends on the number of correlated initial variables and the maximum justifiable variance.PC1s usually maximize the variation.Therefore,the number of main components can be significantly reduced compared to the initial variables.

4 k-means algorithm

The k-means approach(Ball and Hall 1967;Mac Queen 1967)is one of several clustering methods used in data mining.K-means clustering is considered exclusive and lf at.Samples are clustered into a number of specific clusters(k),calculating the sum of Euclidean distance to minimize each sample from the center of its cluster(Chen and Chien 2010).The k-means algorithm starts with a certain number of clusters and endeavors to achieve cluster centers that are the average points of their respective clusters.The initial number of clusters is randomly selected.Each data point is assigned to one of the clusters based on greater similarity,and new clusters are obtained.This process can be repeated and in each replication,new centers are calculated by averaging the data and reassigning data points to new clusters(Egozcue et al.2003).The processing algorithm is as follows:

1. There is a set of N data points in multidimensional space.

2. An integer,k,points are chosen to be cluster centers.

3. Means of the clusters are calculated as centroids.

4. Sum of squares Euclidean distance is calculated from the center of clusters.

5. Each sample is assigned to the cluster whose average has the least within-cluster sum of squares.The goal is to minimize the mean squared distance from each sample to the nearest center.

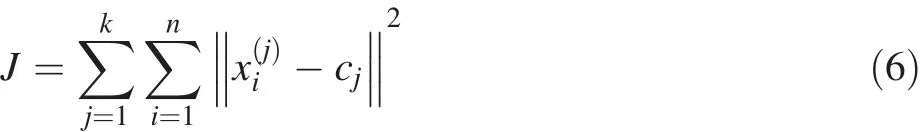
where cjis the centroid of the cluster and x is the data in the cluster,and||||indicates distance.

6. Calculate new means based on the new clusters.

In this study,we used efficient criteria—known as silhouette criteria—to specify the appropriate number of clusters(k)in the data set.Rousseeuw(1986)presented this method;the silhouette method can group all samples well,even the ones located between clusters.

4.1 Definition of silhouette

Initially,all data were classified and put into k clusters.The silhouette,S(i),is a measure of how well the data are assigned to their respective clusters and can be computed as follows(Rousseeuw 1986):

where a(i)is the average dissimilarity of the sample to all other samples in the same cluster and b(i)is the minimum average dissimilarity of the sample to all other clusters to which the sample is not a member.Since b(i)depends on comparison with other clusters,the number of clusters,k,must be more than one.The equation can be written as:

where S(i),is between-1 and+1.If S(i)is around+1,the sample is in an appropriate cluster;a negative S(i)indicates the desired sample is in the wrong cluster;and an S(i)=0 indicates that the desired sample fi ts equally in multiple clusters.

5 Datasets

About 256 stream sediment samples were analyzed by Inductively Coupled Plasma Mass Spectrometry for 32 elements by the fire assay method(Fig.1).The distributions are not normal.The data,which were normalized by taking logarithms,and their statistical characteristics are presented in Table 1.We used MATLAB and SPSS software to analyze through k-means and PCA the elemental stream sediment data and ultimately to estimate the grade of gold.

6 Results and discussion

6.1 Correlation coefficient analysis results

A correlation coefficient illustrates inter-element relationships and correlations.It can reveal some interesting information about the sources of metals(Rodrı´guez et al.2008).Spearman’s correlation coefficients rank as follows:significant correlation(0.5–1.0 and-1.0 to-0.5)which are bolded in Table 2,medium correlation(0.3–0.5 and-0.5 to-0.3),low correlation(0.1–0.3 and-0.3 to-0.1),and uncorrelated(0.0–0.09 and-0.09 to 0.0;Fei et al.2014).The results of the Pearson correlation coefficients between fi fteen evaluated elements are in Table 2.

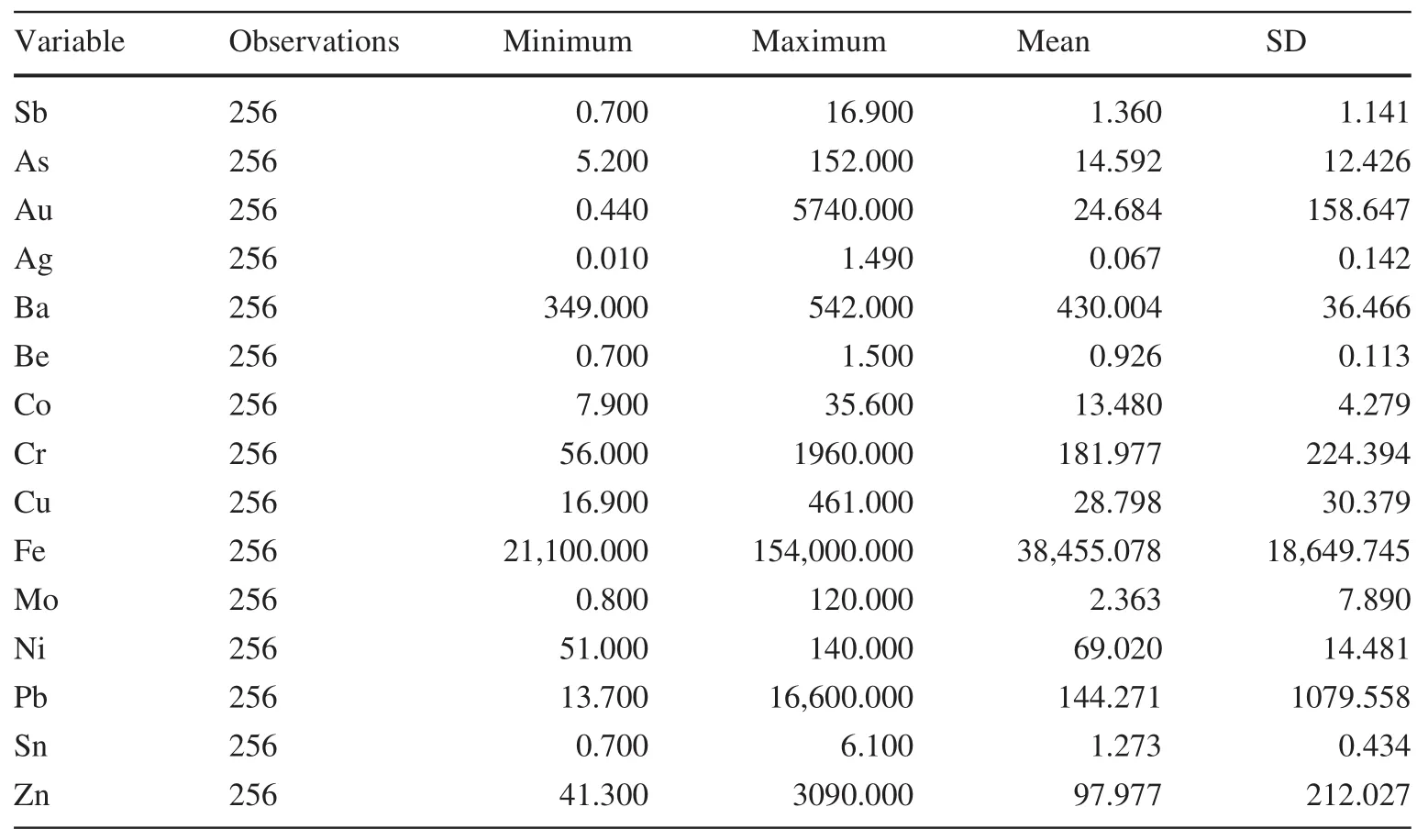
Table 1 Statistical characteristics of elements in the Khooni district(raw values)

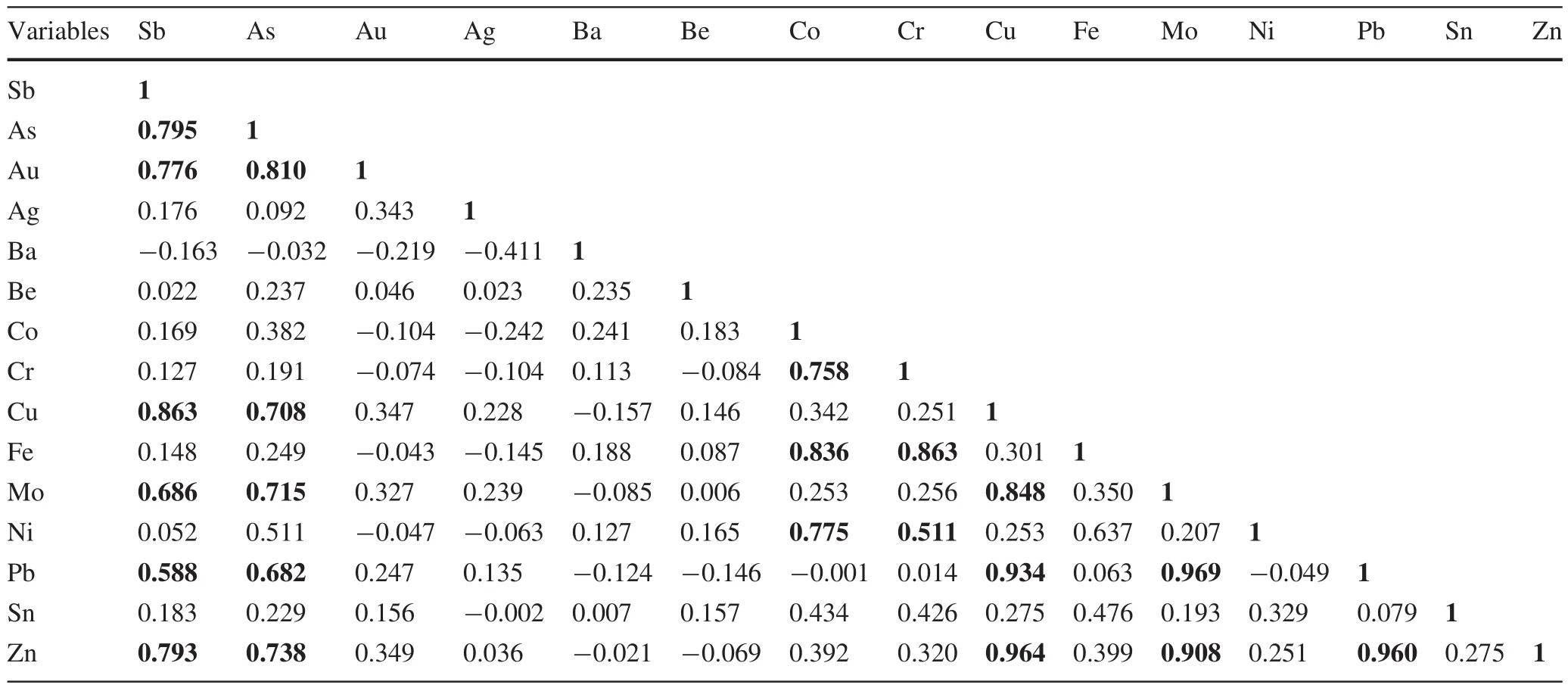
Table 2 Pearson correlation coefficients of elements in the Khooni district

Correlation coefficients were calculated for the stream sediment samples.These coefficients indicated a significant positive correlation among some elements,such as Au–As(0.810),Au–Sb(0.776),and Sb–As(0.795)which are bolded in Table 2.The relationships between these elements indicate they might feasibly have the same source;the geochemistry is similar across the study area(Mahvash Mohammadi and Hezarkhani 2015).In addition,there are relatively strong correlations between Cu,Mo,Pb,and Sb.

6.2 Principal component analysis

A scree plot(Fig.2)shows that the eigenvalues of the fi rst four components are greater than one,and account for about 85.27%of the total variance of data.With the criteria of eigenvalue greater than 1 and percentage of variance as explained in Table 3,four principal components were selected,which are bolded in Table 3.The first coefficient(F1)from fifteen components had the highest percentage of variability in the area.PCA was used for the concentrations of Au,As,Ag,Sb,Ba,Be,Co,Cr,Cu,Fe,Mo,Ni,Pb,Sn,and Zn to reduce dimensions and classification.PCA results are presented for all four components in Table 4.

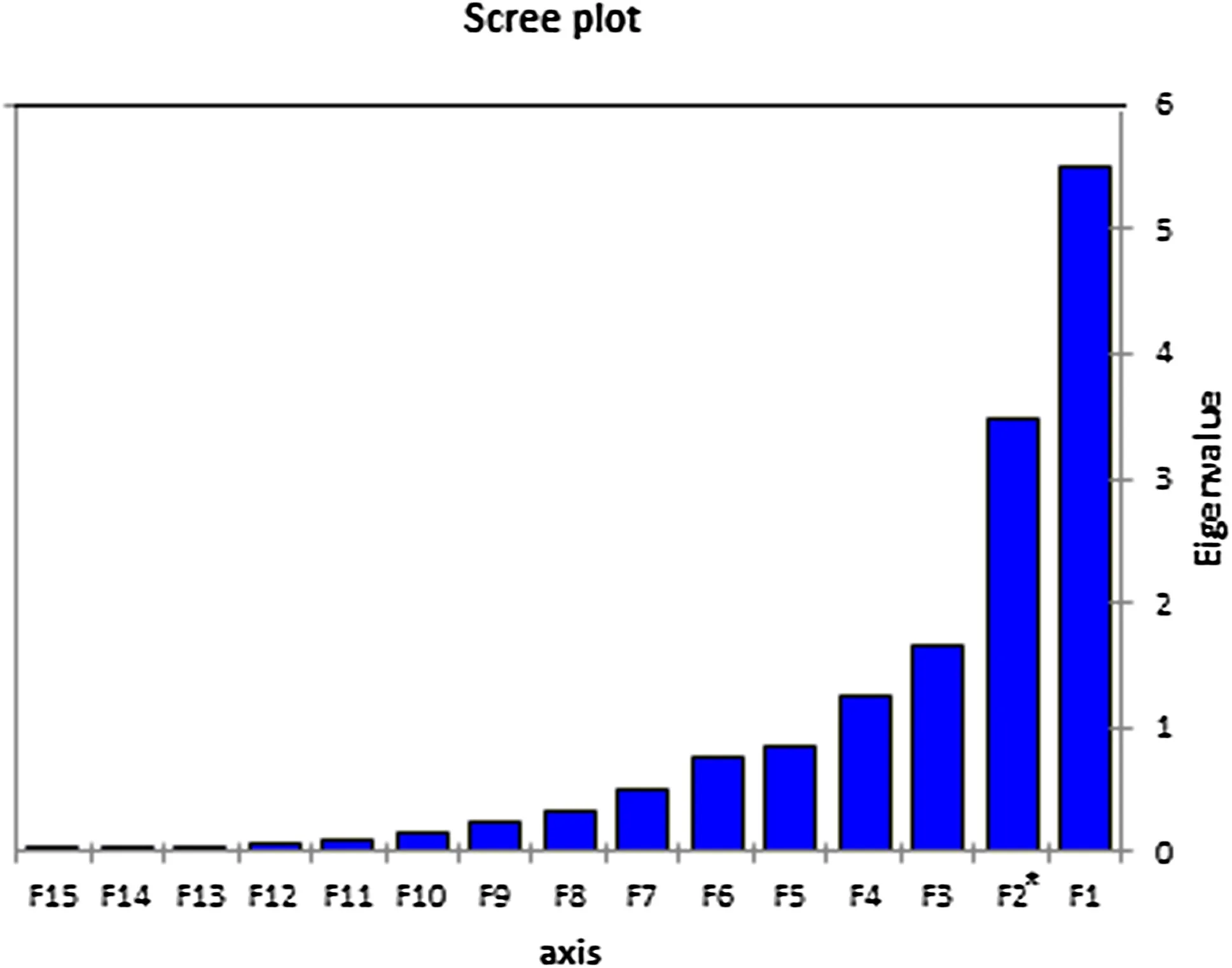
Fig.2 Scree plot of elements in the Khooni district

As shown in Tables 3 and 4,the first component(PC1)accounted for 38.74%of the total variance with strong loadings on Au(0.973),Sb(0.933),and As(0.870)and mediocre loadings on Cu(0.652),Mo(0.625),Pb(0.646),and Zn(0.658).As shown in Table 4,the amount of strong loading,greater than 0.5,are bolded.The behaviors of elements in this group were highly dependent,with a strong positive correlation between them.PC2 accounted for 25.187%of the total variance,loaded heavily on Co(0.922),Cr(0.836),Fe(0.864),Ni(0.747),and Sn(0.550).PC3 had high loadings only on Ag(0.870)and accounted for 13.019%of the total variance.PC4 accounted for about 8.331%of the total variance and had loadings on Ba(0.701)and Be(0.781).

Figure 3 shows loading plots of elements in the space defined by two components.As shown in Fig.3a,As and Sb are close to Au;Cu,Mo,and Zn are close to Pb;Ni,Cr,Co,Fe,and Sn are in a group;and Ba and Be are near each other.These groups suggest Au,As,and Sb have strong relationships;other groups of elements suggest the distribution of these elements is related.Likewise,in Fig.3b,Cr,Co,Fe,Sn,and Ni make a group—an association of correlated elements.A good correlation exists between Ba and Be(Fig.3c).Ag is separate and does not fall into any group.The PCA agreed with the cluster analysis,with eachproducing strong clusters and the same element groupings.Au,As,and Sb,which share paragenesis,are in a cluster and have a strong relationship.

Table 4 Factor loadings of elements in Khooni district

6.3 K-means results

In the present study,we used k-means to cluster stream sediment samples of the Khooni area and calculate the optimum k for three elements—gold,arsenic,and antimony—according to the coordinates of the sampling points.The silhouette criterion was used to determine the number of clusters(k);k was varied from 3 to 10.Then,the results were analyzed to select the optimum k.Figure 4 shows average silhouette value based on the number of clusters.The cluster with the maximum average silhouette value was selected as the optimum cluster.According to the above text,if the value of the average silhouette is close to 1,the samples have been clustered correctly.Figure 4a exhibits the average silhouette values for arsenic and antimony;clustering with k=3 is selected as the optimum k,because of the high associated average silhouette value,0.8584.Similarly,k=3 with 0.9647 average silhouette,and k=4 with 0.8064 were chosen as the optimum numbers of clusters for coupling gold and antimony(Fig.4b),and for coupling gold and arsenic(Fig.4c),respectively.

Table 3 Eigenvalue and percentage of variance of elements in the Khooni district

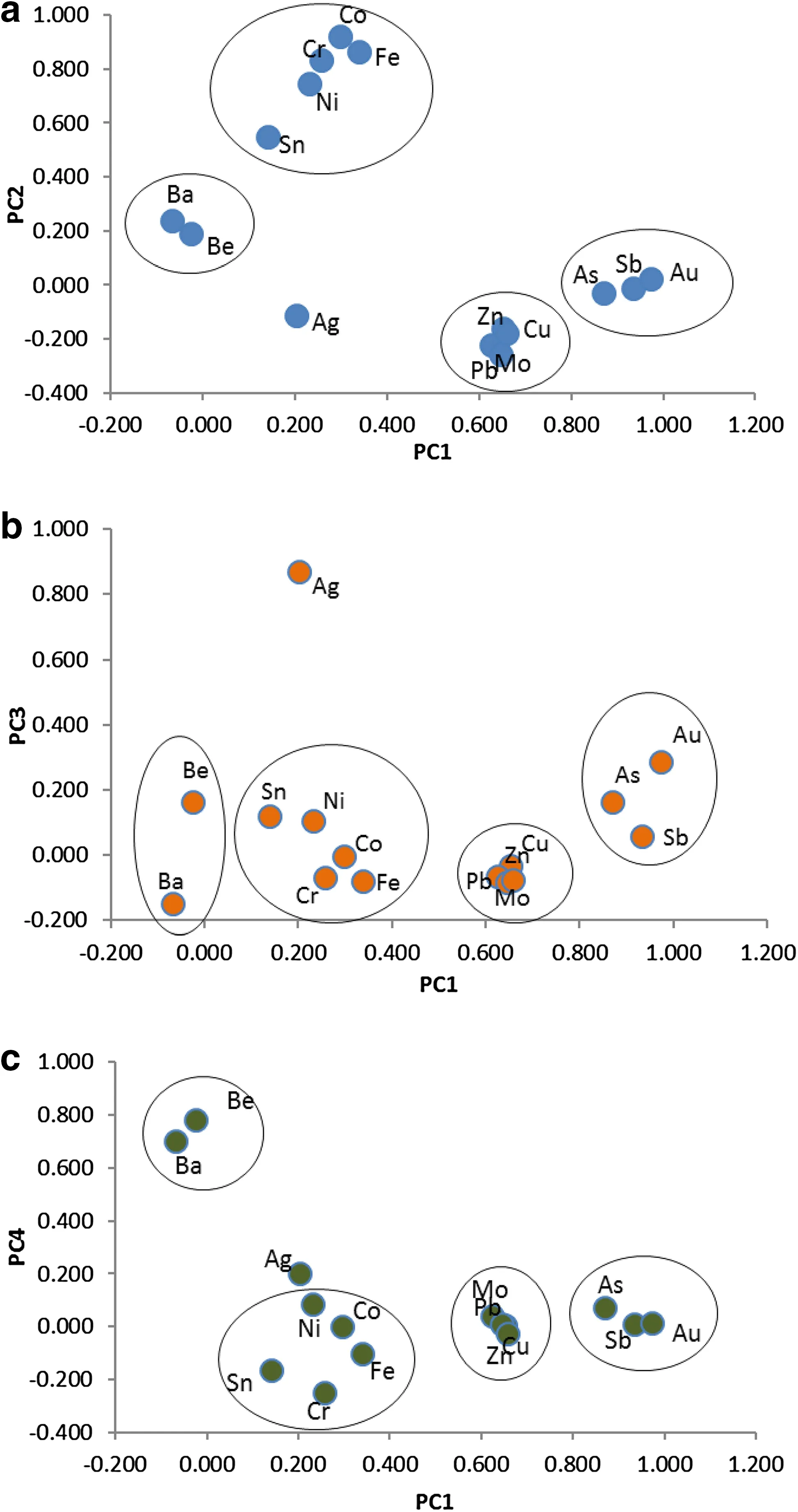
Fig.3 Loading by plot of elements Khooni district

All data were classified by k-means and then the centroids of each cluster were calculated.The diagram of centroids is shown for gold and arsenic with k=4(Fig.5a),for gold and antimony with k=3(Fig.5b),and for arsenic and antimony with k=3(Fig.5c).

With increasing grade of gold in Fig.5a,the grade of arsenic increases and subsequently decreases.The best regression is a quadratic curve of y=-0.1158x2+8.5502x-4.756with a correlation coefficient R2=0.9625.

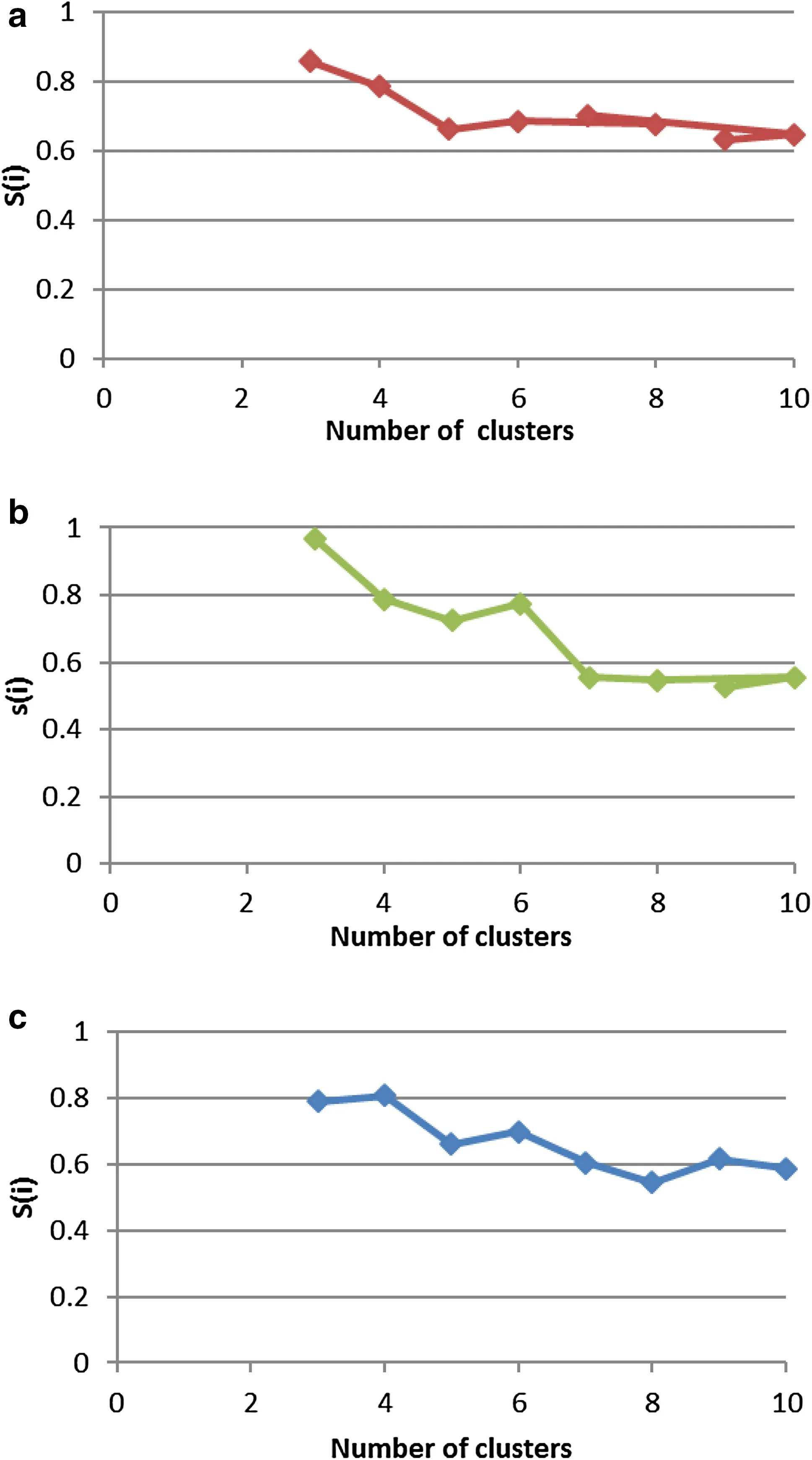
Fig.4 Changes in the value of S(i)based on the number of clusters a arsenic and antimony,b gold and antimony,c gold and arsenic

The behavior of gold and antimony is similar to the behavior of gold and arsenic(Fig.5b);with increasing gold grade,the grade of antimony initially increases and later decreases.The best regression is a quadratic curve with a negative concavity y=-0.0012x2+0.0928x+1.134and a correlation coefficient R2=1.The behavior of arsenic and antimony is predictable according to previous results.As a result,we expect these two elements to have a direct relationship.The grade of arsenic increases with increased grade of antimony.The best regression plotted on centroids was y=0.0274x+0.9713with a correlation coefficient R2=0.9992(Fig.5c).

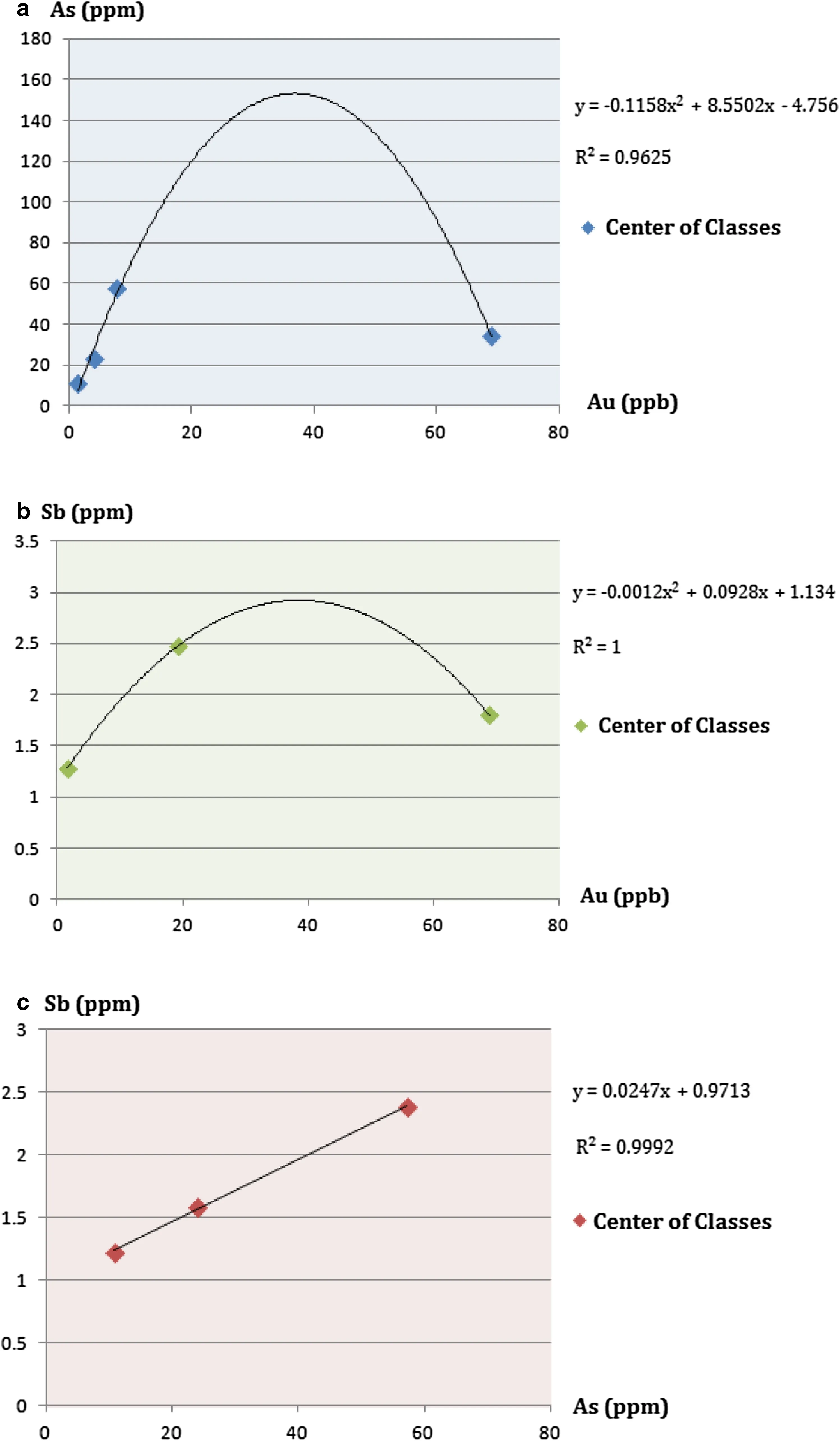
Fig.5 The best regression curve a k=4 classifications relating to Au and As;b k=3 classi fi cations relating to Au and Sb;c k=3 classifications relating to Sb and As

7 Estimating the grade of gold

Estimating the gold grade depends on the behavior of gold,arsenic,and antimony related to the sample coordinate.In the first step in determining this relationship,the optimum number of clusters was selected by silhouette criteria.The highest value of the average silhouette was 0.6568,belonging to Class 5(Fig.6).The coordinates of the samples along grade elements of gold,arsenic,and antimony were used as input data.The range of coordinate and grade values are thus different.To avoid creating errors in calculations and to obtain the correct estimation,all input values were placed in a standard range—the interval[0,1]—by Eq.9.

The specific cluster centers are given in Table 5 for k=5.

Using multivariate regression in SPSS software to determine the relationship between gold,arsenic,and antimony according to coordinate sampling in the study area,the grade of gold was estimated.Values of gold(the dependent variable)and the amount of arsenic and antimony,and length and width of samples(the independent variables) were introduced into the application.

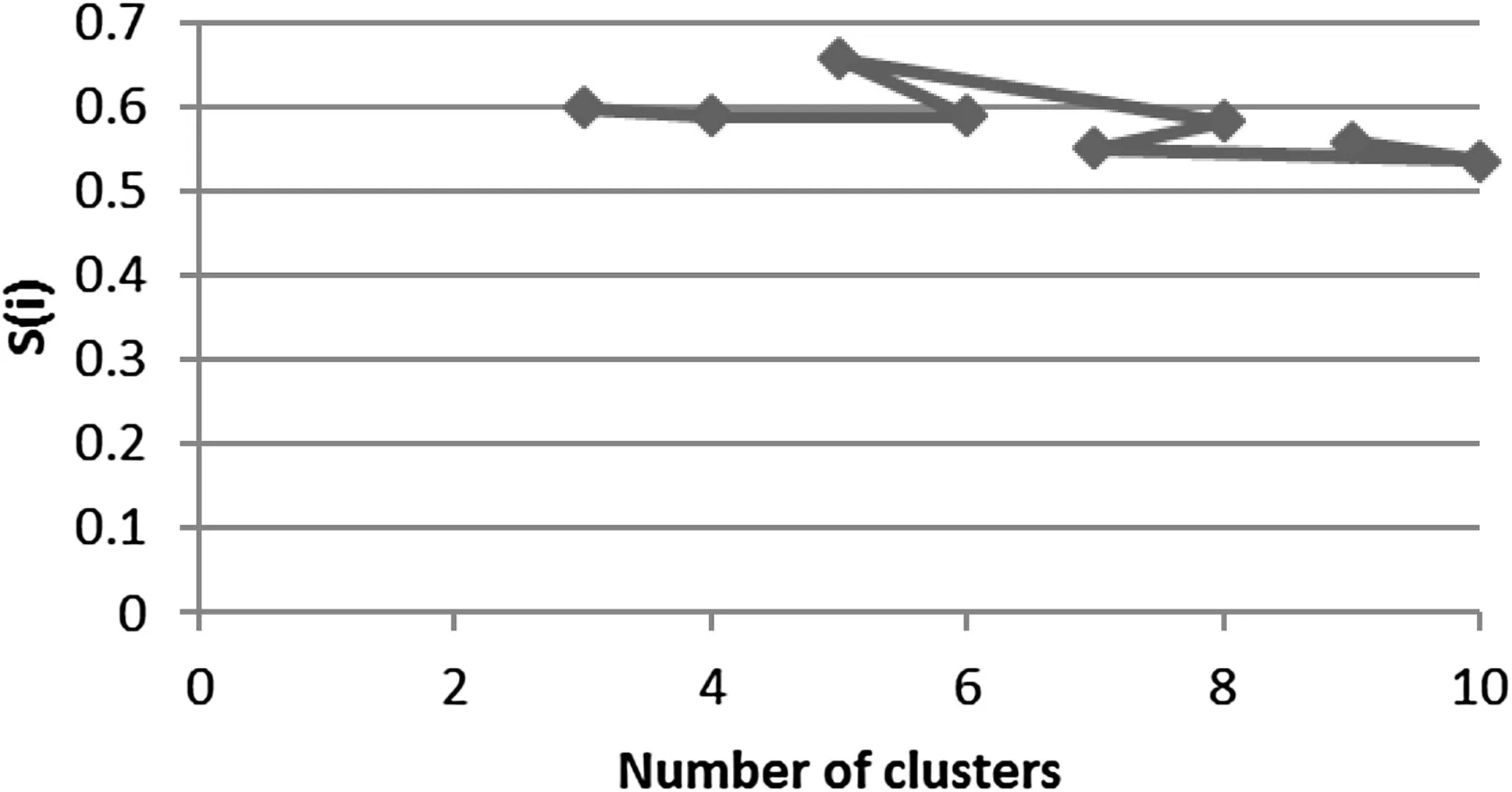
Fig.6 Changes in the value of S(i)based on the number of clusters(for gold,arsenic,and antimony)

Specification and multivariate regression coefficients were calculated and are reported in Table 6.

According to the coefficients in Table 6,the formula of multiple regressions was determined as follows:

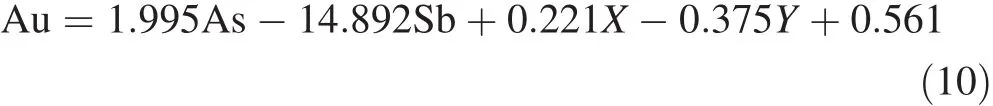
The R2suggests the regression model could explain the changes to Au.At this point,R2=73.72,thus 73%of changes to the gold value(y)are based on the value of X(arsenic,antimony,length and width of the sample).

To validate the estimation of gold,some original data were estimated based on Eq.10 to describe the accuracy.Some data were validated(Fig.7).We randomly selected 30%of the samples and estimated the grade of gold based using the grade of arsenic and antimony and length andwidth of the samples.The computed values were then compared with original values,resulting in a correlation coefficient of 91%(Fig.7).The estimated values of gold almost match the original values of gold,demonstrating the accuracy of the applied method.

Table 6 Specifications and multivariate regression coefficients

Fig.7 Scatter plot of the measured gold values against estimated values for validation

Table 5 Speci fi cation of cluster centroids(clustering by k=5)

8 Conclusion

Due to the evidence of gold mineralization in the Khooni district,estimating Au concentration is important.Elements were divided into five groups including Au,As,and Sb;Fe,Mo,Cu,and Pb;Ni,Cr,Co,and Sn;Be and Ba;and Ag in a group of its own.Based on paragenesis of Au with As and Sb and the results of our analysis,As and Sb were considered for estimating Au concentration.District Through PCA and k-means,an equation was achieved for estimating the gold grade based on arsenic,antimony,and length and width of the samples:Au=1.995As-14.892Sb+0.221X-0.375Y+0.561with a correlation coefficient of 91%.

AcknowledgementsThe authors thank the editors and anonymous reviewers for their constructive comments,which have significantly improved the manuscript.

Abolhassani B,Salt JE(2005)A simplex K-means algorithm for radio-port placement in cellular networks.In:Canadaian Conference on Electrical and Computer Engineering

Adib D(1972)Khooni mine mineralogy,Ph.D.Thesis,University of Shiraz,Shiraz(in Persian)

Bagheri H,Moore F,Alderton DHM(2007)Cu–Ni–Co–A-(U)mineralization in the Anarak area of central Iran.J Asian Earth Sci 29:651–665

Ball GH,Hall DJ(1967)A clustering technique for summarizing multivariate data.Behav Sci 12(2):153–155

Berkhin P(2006)A survey of clustering data mining techniques.In:Kogan J,Nicholas C,Teboulle M(eds)Grouping multidimensional data.Springer,Berlin,pp 25–71

Chen TW,Chien SY(2010)Bandwidth adaptive hardware architecture of K-means clustering for video analysis.IEEE Trans VLSI Syst 18(6):957–966

Crosta AP,Rabelo A(1993)Assessing landsat/TM for hydrothermal mapping in central western,Brazil.In:processing of the 9th thematic conference of geologic remote sensing

Darvish M(2011)Mineralogy studies and determine Khooni skarn sources-North East of Anarak,Esfahan province.M.Sc.Thesis,University of Esfahan,Esfahan,p 153(in Persian)

Davis BM,Jalkanen GJ(1988)Nonparametric estimation of multivariate joint and conditional spatial distributions.Math Geol 20(4):367–381

Ding C,He X(2004)K-means clustering via principal component analysis.In Appearing in proceedings of the 21st international conference on machine learning,Banff

Du Q,Flower EJ(2008)Low-complexity principal component analysis for hyperspectral image compression.Int J High Perform Comput Appl 22(4):438–448

Egozcue JJ,Pawlowsky-Glahn V,Mateu-Figueras G(2003)Isometric logratio transformations for compositional data analysis.Math Geol 35:279–300

Fei Q,Hongbing J,Qian L,Xinyue G,Lei T,Jinguo F(2014)Evaluation of trace elements and identi fi cation of pollution sources in particle size fractions of soil from iron ore areas along the Chao River.J Geochem Explor 138:33–49

Hartigan JA(1975)Clustering algorithms(probability&mathematical statistics).Wiley,London

Hartigan JA,Wong MA(1979)A K-means clustering algorithm.J R Stat Soc 28(1):100–108

Heydarian Dehkordi N,Rassa A(2011)Study of alteration and investigating genetic between gold and other elements in khooni district.J Appl Geol Iran 2:95–106(in Persian)

Heydarian Dehkordi N,Rassa A(2012)Characteristics and genesis of gold mineralization in Eocene volcanic units of khooni Cheshmeh,Anarak,the nature of mineralizing fluids and comparison with other types of gold deposits.J Geol Iran 17:73–85(in Persian)

Hotelling H(1933)Analysis of a complex of statistical variables into principal components.J Educ Psychol 24:417–441

Howarth RJ,Sinding-Larson R(1983)Statistic and data analysis in geochemical prospecting.Handb Explor Geochem Amesterdam 2:207–289

Jolliffe IT(1986)Principal component analysis.Springer,New York

Jolliffe I(2002)Principal component analysis for special types of data.In:Principal component analysis,2nd edn.Springer,New York,pp 338–372

Labib K,Vemuri V(2005)Application of exploratory multivariate analysis for network security.In:Vemuri V(ed)Enhancing computer security with smart technology.CRC Press,Boca Raton,pp 229–261

Lin JW(2012)Study of ionospheric anomalies due to impact of typhoon using principal component analysis and image processing.J Earth Syst Sci 121(4):1001–1010

Lloyd S(1957)Least squares quantization in pcm.Bell Telephone Laboratories Paper,Marray Hill

Loska K,Wiechuła D(2003)Application of principal component analysis for the estimation of source of heavy metal contamination in surface sediments from the Rybnik Reservoir.J Chemosphere 51:723–733

Loughlin WPG(1991)Principal component analysis for alteration mapping.Photogram Eng Remote Sens 57(9):1163–1169

MacQueen J(1967)Some methods for classi fi cation and analysis of multivariate observations.In:Proceedings of the 5th Berkeley symposium on mathematical statistics and probability,California,vol 1,pp 281–297

Mahvash Mohammadi N,Hezarkhani A(2015)Estimation of grade gold in Khooni deposit using the behavior of gold,Arsenic and Antimoney elements by clustering K-means method.J Anal Numer Methods Min Eng 5(10):77–92(in Persian)

Mahvash Mohammadi N,Hezarkhani A,Shokouh Saljooghi B(2016)Separation of a geochemical anomaly from background by fractal and U-statistic methods,a case study:Khooni district,Central Iran.Chem Erde/Geochem 76:491–499

Malyszko D,Wierzchon ST(2007)Standard and genetic K-means clustering techniques in image segmentation.In:6th International conference on computer information systems and industrial management applications

Nezampoor H,Rasa A(2005)Study of gold mineralization in oxide veins Khooni–Anarak region.In The twenty-fourth national geosciences symposium(in Persian)

Ng A,Jordan M,Weiss Y(2001)On spectral clustering:Analysis and an algorithm.In:Proceedings of the neural in formation processing systems

Pak HAA,Sharafeddin M(2005)Exploration data analysis.Tehran University Press,Tehran(in Persian)

Pasadakis N,Obermajer M,Osadetz KG(2004)Definition and characterization of petroleum compositional families in Will is ton Basin,North America using principal component analysis.JOrg Geochem 35:453–468

Pham TD(1997)Grade estimation using fuzzy-set algorithms.Math Geol 29(2):291–305

Pourjabar A(2005)Geochemical investigations on the polymetalic vein in Khooni(Esfahan Province),M.Sc Thesis,Amirkabir University of Technology,Tehran,p 217(in Persian)

Prinzhofer A,Mello MR,Da Sila Freitas LC,Takaki T(2000)A new geochemical characterization of natural gas and its use in oil and gas evaluation.In:Mello MR,Katz BJ(eds)Petroleum systems and south Atlantic Margins.American Association of Petroleum Geologists Bulletin,Memoir 70:107–119

Rodrı´guez JA,Nanos N,Grau JM,Gil L,Lo´pez-Arias M(2008)Multiscale analysis of heavy metal contents in Spanish agricultural topsoils.Chemosphere 70:1085–1096

Rousseuw PJ(1987)Silhouettes:a graphical aid to the interpretation and validation of cluster analysis.Comput Appl Math 20:53–65

Sabeti H,Javaherian A,Araabi ND(2007)Principal component analysis applied to seismic horizon interpretations.International Congress of Petroleum Geostatistics,Cascais,pp 10–14

Templ M,Filzmoser P,Reimann C(2008)Cluster analysis applied to regional geochemical data:problems and possibilities.Appl Geochem 23(8):2198–2213

Tipping ME,Bishop CM(1999)Probabilistic principal component analysis.J R Stat Soc B 61:611–622

Xiaoya Z,Chunlai L,Chang L(2009)Quanti fi cation of the chemical composition of lunar soil in terms of its re fl ectance spectra by PCA and SVM.Acta Geochim 28:204–211

Yeung KY,Ruzzo WL(2001)Principal component analysis for clustering gene expression data.Bioinformatics 17:763–774

Zha H,He X,Ding C,Simon H,Gu M(2001)Spectral relaxation for K-means clustering.Technical Report TR-2001-XX,Pennsylvania State University,University Park,PA