重视数形结合 培养数学素养

毛建铭

（福建省德化县实验小学，福建泉州 362500）

引 言

随着新课标的实施，在小学数学教学中要求注重培养学生的数学核心素养，既要学习数学知识，更要注重培养其数学思维能力与解决问题的能力。为此需要教师更新教学理念，注重运用多种方式方法来培养学生的数学素养。数形结合的思想方法作为数学重要的思想方法，能提高学生数学学习兴趣，能够有效帮助学生理解数学概念，记忆数学规律，提高学生数学思维能力，能把复杂问题简单化，把抽象问题具体化，从而提高解题效率。笔者结合小学数学教学实践，对利用数形结合思想方法培养学生数学素养进行了深入探索。

一、数形结合对培养学生数学素养的意义

数形结合的思想方法是数学重要的思想方法之一，学习掌握数形结合思想方法，对学生数学学习有重要作用，有利于培养学生的数学核心素养[1]。

一是促进教学目标的实现。在数学教学中，概念、规律的教学比较抽象，小学生不易理解掌握，也容易让学生感到数学学习枯燥乏味。运用数形结合的方法，从“数量”和“图形”两个方面对数学知识进行理解，以数辅形，以形想数就能深入理解数学概念、规律的本质和内在联系，有效突破教学的难点问题。

例1 ，有一个长方体，假如把它的高增加2 cm，则这个长方体就变成了正方体，并且它的表面积会比原来增加56 cm2，求原来长方体的体积是多少？

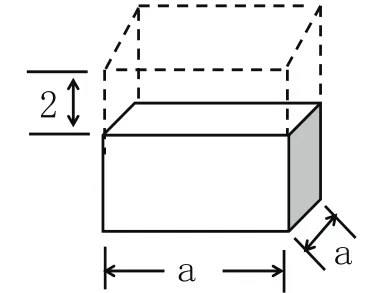
图1

此题时许多学生找不到解题思路，不知如图1

分析：在解 何下手才能找到长方体原来的长、高、宽。如果能引导学生画出图形，就可以看出原图形的长和宽相同，增加的表面积是由4个长方形组成，每个长方形的面积是2a，则4×2a=56，则a=7，这样就知道原图形的长和宽是7 cm，高就是5 cm，原长方体的体积就是7×7×5=245 cm3。

二是能培养学生的数学思维能力。数学学习的核心是培养学生的数学思维能力，数形结合能有效培养学生的数学思维能力。数形结合既具有形象直观的特点，又具有精确严密的特性，把数和形结合能培养学生的形象思维和直觉思维，使学生的思维能力得到有效发散，为应用数学知识分析和解决问题奠定良好的思维基础。

三是能提高学生的数学解题能力。学习数学目的在于应用，数学知识的掌握影响着学生解决问题能力的提高，而数学思想方法的运用和掌握同样对学生解决问题的能力有重要影响。运用数形结合的思想方法有助于学生找到解题的方法和突破口，缩短思维的时间，提高解题效率，从而能有效提高数学解题能力，对提高学生的数学素养有重要的作用。

二、数形结合方法在数学教学中的应用

1.以形助数，丰富学生数学思维内涵

“以形助数”就是借助于图形的形象直观性来处理抽象的代数问题。但是在求解代数问题时，它不像几何问题那样容易让人想到“数”与“形”两者之间的转化，需要教师在平时的学习中注重渗透数形结合的思想方法，通过对数学思想方法的运用来培养和发展学生的数学思维能力。运用图形形象直观的特性，可以有效帮助学生在代数解题时快速有效地找到解题思路，降低解题的难度，增强学生学习的兴趣，使学生对数学概念、规律、算理的理解更深入、更全面。

例2，在学习真分数与假分数时，由于这两个概念比较抽象，对于小学生来说，不容易理解。要让学生真正理解其概念和意义，同时又容易让学生接受，可以采用数形结合的方法。把1个大正方形看作是单位“1”，通过运用不同的图形，让学生真正理解真分数是小于1的，假分数是大于1的，这样很自然地就能让学生掌握真假分数的概念和特性。比如，可用图2-1表示真分数用图2-2表示1，用图2-3表示假分数教师还可以运用类似的图形让学生涂色。这样学生通过对图形的观察分析，增强感性认识，在此基础上进行抽象概括，就能形成对分数的分子、分母大小关系的3种不同情况：就能理解分子＜分母时，是真分数；分子＞分母时是假分数；分子＝分母时是1。可见数形结合对理解掌握数学知识非常有益。

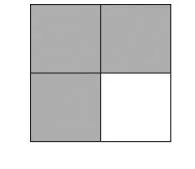
图2-1

图2-2

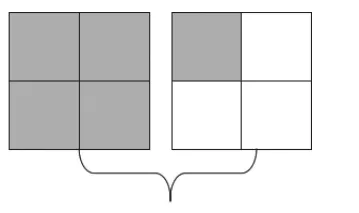
图2-3

在学习几何图形知识时，通过对图形的变换可以让学生更好地理解几何图形的面积、体积公式等。

例3，在学习梯形面积公式时，可让学生进行合作探究，通过对图形分割、拼接等，学生就能借助图形掌握梯形面积的多种求解方法，能有效拓展学生的思维能力，增强解决数学问题的灵活性。如，可以把梯形分割成如图3所示的三种情况：在（1）中把梯形分成一个矩形和两个直角三角形；在（2）中分成一个平行四边形和一个三角形；在（3）中分成了两个三角形。学生已经学过三角形面积、矩形面积、平行四边形面积的求解公式，通过分别求各个图形的面积，再相加就是梯形的面积。借助图形可以用多种方法推导出梯形面积公式。

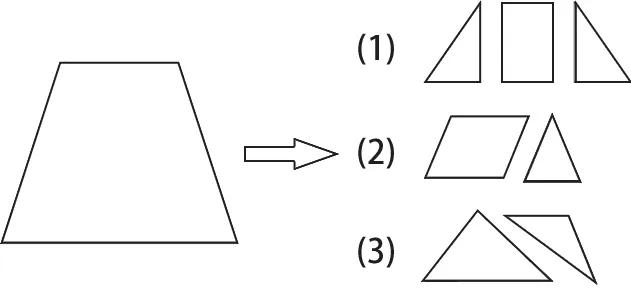
图3

2.以数解形，培养学生的数学应用能力

“以数解形”是利用“代数”的精确严密性来揭示“图形”中蕴含的数量关系，从而能找到图中的某些属性[2]。如果借助代数的运算来解答几何问题，既能增强解题的准确性，又能降低一些问题的难度。

例4，在图4所示的图形中，当一个人从A点出发要到达B点，它可以选择按照①号路线和②号路线行走，问学生走哪条路线距离最短？

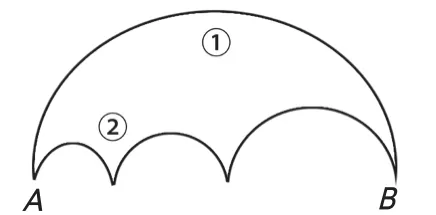
图4

解析：在求解此题时，如果让学生从图形上直接观察，很难得出正确结论，即使一些学生能猜到答案，学生的脑子里也没有理论上的根据。对于这个图形问题，教师可引导学生运用代数运算的方法进行精确的计算。

根据图形可假设大圆直径是10，三个小圆的直径分别是2、3、5，然后分别计算两条路线的路程，①号路线：10×л÷2=5л； ② 号 路 线：（2×л÷2）+（3×л÷2）+（5×л÷2）=5л。由此可见，两条路线的路程相等。通过用代数的方法进行计算，使学生容易理解，从而提高其数学解题能力。

三、数形结合思想方法教学策略

数形结合的思想方法对培养学生的数学素养具有重要作用，需要教师在数学教学中逐渐渗透，让学生在反复的运用中体验和理解。一是在课堂教学中渗透数形结合的思想方法。要在知识的形成阶段渗透数形结合的思想方法，在数学的概念规律推导阶段提示数形结合的思想方法，在知识的归纳总结阶段概括数形结合的思想方法。二是在练习或习题中发展学生的数形结合的思想方法。既要注重在课堂练习中提供数形结合的练习时机，又要注重在课后作业题中进行数形结合练习。通过反复练习，学生才能树立数形结合的思想并能在解题中运用。

结 语

数形结合作为重要的数学思想和解题方法，在教学中加强其运用对培养学生的数学素养有着积极的作用，需要教师长期反复地运用，学生才能熟练掌握。

[1]王舒瑶.数形结合思想在小学数学教学中的应用研究[D].西南大学,2015.

[2]黄秀华.巧用数形结合,培养小学生的数学素养[J].数学大世界(下旬),2016,(08):27.