基于迟延估计与Kalman状态跟踪的热工过程动态数据驱动建模

董 泽， 尹二新，

(华北电力大学 河北省发电过程仿真与优化控制工程技术研究中心, 河北保定 071003)

随着火电机组单机容量和参数的提高以及系统本体的复杂化，为有效保证热力系统的安全、稳定和经济运行，对热工过程对象的控制水平提出了更高的要求。其中对热工控制系统进行设计、优化及性能分析，建立热工过程的准确模型是关键。热工对象一般具有大惯性、长时滞和非线性等特点，建模较为困难。

秦志明等[1-2]通过机理分析建立了火电机组协调控制系统的非线性模型；范永胜等[3]通过对锅炉过热汽温系统进行机理分析，得到了过热汽温对象的传递函数模型。但上述建模方法建模过程复杂，参数难以确定，且对系统进行了简化，并忽略了纯迟延环节。

Simani等[4]对燃气轮机进行了最小二乘算法系统建模。王新等[5]综合应用输出误差状态空间模型辨识法(MOESP)与子空间辨识数值算法(N4SID)，对某天然气电站和Alstom气化炉进行了模型辨识。以上建模方法均基于最小二乘算法，需对热工过程对象加入特定扰动信号，会对大型火电机组的运行安全产生不利影响。

随着火电机组监控信息系统的发展，大量运行数据被保存到历史数据库中，这些数据包含反映热工过程对象结构及参数的信息，利用这些数据进行热工过程对象辨识已成为当今研究的热点。在该背景下，人工神经网络(ANN)、偏最小二乘(PLS)和支持向量机(SVM)等算法在热工过程对象建模中得到了广泛应用。Liu等[6]针对1 000 MW超超临界直流锅炉采用2种不同结构的神经网络进行建模。曲亚鑫等[7]基于再热汽温历史数据及偏最小二乘算法，提出一种再热汽温反向建模方法。秦天牧等[8]应用改进偏互信息(IPMI)法，选取最优变量集作为SVM模型的输入，并利用历史数据建立了SCR脱硝系统的IPMI-SVM模型。但上述模型均属于非参数模型，通用性差，应用场合较为局限。

为解决上述方法对对象动态特性描述不够准确的问题，利用历史数据对热工过程进行传递函数建模的方法随之出现[9]，为基于智能信息处理的热工过程建模技术提供了新思路。袁世通等[10-12]利用火电机组历史数据和智能寻优算法对多个热工控制系统进行了建模，但其要求应用系统由稳态到动态的历史数据段作为建模数据，而对于许多复杂热工过程而言，系统长时间处于非稳定状态，无法获取系统稳态数据，且即便历史数据库中存在少量的稳态数据，对该数据段的筛选工作量巨大，因此无法应用上述方法辨识热工对象模型。

基于上述问题，笔者提出一种基于迟延估计与Kalman状态跟踪的热工过程动态数据驱动建模方法。该方法选取历史数据中系统输入输出的动态响应数据进行模型辨识，并将数据末端的系统输入作为输入数据的稳态分量，将输出数据稳态分量、热工对象纯迟延时间及热工对象模型参数作为寻优变量。首先，依据预估纯迟延时间对建模数据进行平移处理，依据建模数据末端的系统输入与预估的输出稳态分量，对数据进行去稳态分量处理，然后将建模数据分为3段，应用Kalman滤波算法预估第一段数据末端的系统状态，作为第二段数据的系统初态，应用第二段数据进行模型参数辨识，应用第三段数据进行模型验证。最后对某600 MW火电机组过热汽温惰性区模型进行辨识。

1 建模方法

利用热工过程的历史数据进行传递函数建模时一般选取历史数据中系统由稳态过渡到动态的响应数据作为建模数据，采用智能寻优算法对预估模型的参数进行修改，使得预估模型输出接近实际输出，当无法获取稳态数据或稳态数据筛选困难时无法应用该方法进行模型辨识。应用动态数据进行模型辨识可以有效解决数据获取的问题，但需要解决动态数据建模存在的3个问题：系统纯迟延时间的获取、建模数据中系统稳态分量的剔除和动态数据中系统初始状态的获取。

对热工对象而言，受化学反应时间及物料输送时间的影响，大部分热工过程均存在不同程度的纯迟延，而对纯迟延系统的建模历来是模型辨识领域的难题，部分文献中应用惯性环节对模型的纯迟延部分进行近似[13],这显然是不严谨的。为解决该问题，笔者从数据处理角度出发，将系统的纯迟延时间看成寻优变量的一个维度，应用智能寻优算法改变预估纯迟延时间，再根据该时间对建模数据进行平移处理，从而解决热工对象系统历史数据建模中纯迟延时间的获取问题。

应用热工过程动态历史数据进行建模时，由于系统尚未稳定，无法获取热工系统输入输出的稳态分量值，从而无法对数据进行去稳态分量处理。考虑到大部分热工过程为有自衡对象，假设从所选建模数据末端对应的时刻起，系统输入不再变化，则系统输出经过一段时间的响应后会最终进入稳态，因此，为获取建模数据所对应的系统输入输出的稳态分量，将所选动态数据末端的系统输入作为系统输入的稳态分量，并将系统输出的稳态分量作为寻优环节的一个维度，通过智能寻优算法改变系统输出稳态分量，再根据该分量进行输出稳态分量的剔除。

由于选取建模数据在动态数据段，系统的初始状态未知，因此将建模数据中的一部分数据用于系统的状态估计，并将估计所得状态作为与剩余数据对应的系统初始状态。常用的状态估计方法有Luenberger状态观测器和Kalman滤波算法，为有效克服热工系统历史数据中的噪声干扰，选用Kalman滤波算法作为状态估计算法。为使Kalman状态估计能够应用于传递函数模型，将后者转换为状态空间模型，再将其离散化，获取对象的离散状态方程，从而使Kalman滤波算法与传递函数模型联系起来。

为更清晰地阐述建模过程，结合某热工过程的动态历史数据示意图进行介绍(见图1)。该建模方法流程见图2，建模过程如下：

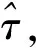
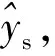
(3) 给定热工对象的预估模型，求取对应离散状态方程，再根据系统的离散状态方程设计Kalman滤波器。应用ab段对应的系统输入输出和Kalman滤波算法对b处系统状态进行估计。

(4) 将所得b处系统状态作为bc段数据对应的系统初始状态，应用bc段数据中的系统输入和系统离散状态方程对系统进行仿真，记录仿真输出。

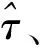
(6) 应用最优参数下的c处系统状态及预估模型，继续对cd段数据进行仿真，比较仿真输出与实际输出，从而达到验证目的。

需要说明的是，由于预估纯迟延时间并非定值，而是随寻优过程不断被修改，再根据修改后的值对建模数据中的系统输出进行平移，当给定的预估纯迟延时间寻优范围足够大，即实际纯迟延时间包含于预估纯迟延时间寻优范围时，智能寻优算法可以找到最佳的纯迟延时间，因此预估纯迟延时间的初值不会对辨识结果产生影响。

另外，虽然建模数据中b点、c点的选取具有很大的宽容度，但仍需人为选取，以保证b点前，有足够多的数据用来观测b点系统的真实状态，同时bc段有足够多的数据用于建模，cd段有足够多的数据用于验证。而模型有足够多的动态数据段可选，一般均分即可满足各环节要求。

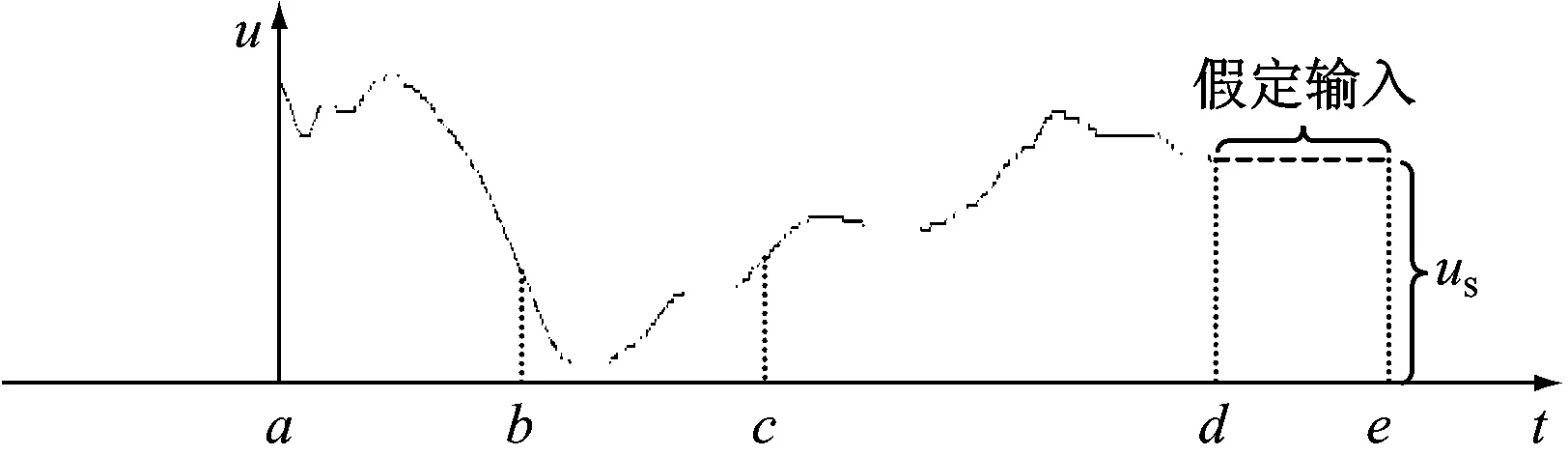
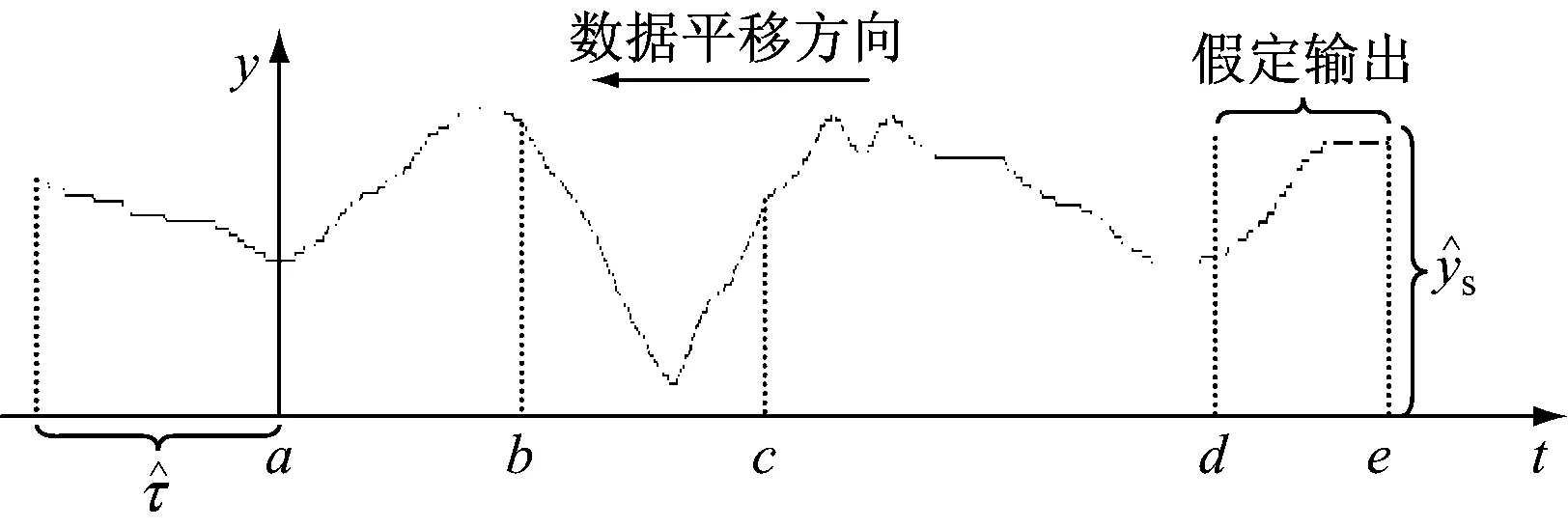
图1 热工过程动态历史数据示意图

2 建模的实现

2.1 Kalman状态跟踪

Kalman滤波算法是一种利用系统离散状态方程，通过系统输入输出观测数据对其状态进行最优估计的算法。该算法是一种预估-校正算法[14]，预估过程可以描述为利用时间更新方程建立对当前状态的先验估计，及时推算当前状态变量和误差协方差估计的值，以便为下一个时间状态构造先验估计值；校正过程负责反馈，利用测量更新方程在预估过程的先验估计值和当前测量变量的基础上建立起对当前状态的改进的后验估计。

设系统离散状态方程如下：

Xk=AXk-1+BUk+Wk

(1)

Zk=HXk+Vk

(2)

式中：Xk为状态变量；Uk为控制输入；Wk为噪声；Zk为观测变量；Vk为观测噪声；A为离散系统矩阵；B为离散控制矩阵；H为离散观测矩阵。

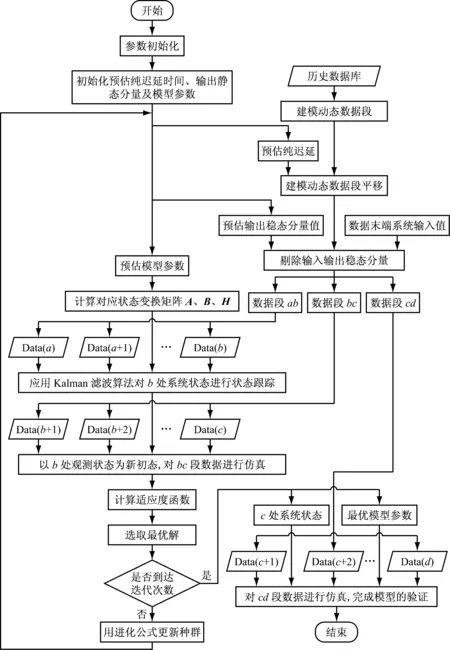
图2 建模流程图

其中，Wk、Zk为相互独立的正态分布白噪声，Wk的协方差矩阵为Q，Zk的协方差矩阵为R，即

Wk～N(0，Q)

(3)

Vk～N(0，R)

(4)

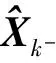
(5)

(6)

先验估计误差和后验估计误差的协方差矩阵Pk-和Pk分别为：

(7)

(8)

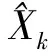
(9)

式中：K为残余增益。

为使式(8)的后验估计误差协方差最小，结合式(6)、式(8)和式(9)，将Pk对K求导，令一阶倒数为零，可得Kk为：

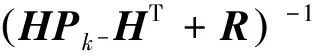
(10)

则Kalman滤波的时间更新方程和状态更新方程为：

(11)

Pk-=APk-1AT+Q

(12)

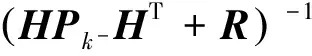
(13)

(14)

Pk=(I-KkH)Pk-

(15)

式中：I为单位矩阵。

对建模数据进行平移及去稳态分量处理后，需要应用Kalman滤波器对ab段数据进行状态跟踪，从而获取b处系统状态。

为使Kalman滤波算法具有普遍适用性，采用通用传递函数模型作为状态跟踪对象，对Kalman状态跟踪过程进行介绍，通用传递函数模型G(s)为：

(16)

式中：n为传递函数分子阶次；m为传递函数分母阶次；s为拉普拉斯算子；a0,a1，…，an-1、b0,b1，…，bm分别为传递函数分母、分子中各阶拉普拉斯算子的阶次。

将传递函数模型转化为能观标准型的状态空间表达式[15]，如式(17)和式(18)所示：

(17)

(18)

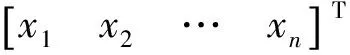
则该连续系统的系数矩阵为：

(19)

式中：Ac为系统矩阵；Bc为控制矩阵；Hc为观测矩阵。

采用零阶保持器对系统状态方程进行离散化，可得系统的离散状态空间系数矩阵[9]如下：

(20)

式中：Ts为采样周期。

需要说明的是，当有足够多的系统输入输出数据时，由于Kalman滤波算法的收敛特性，系统状态初值X0和后验估计误差协方差矩阵P0的选取不影响Kalman状态估计的准确性。且由系统的预估模型可以求取对应的状态变换矩阵A、B和H，再人为给定系统的噪声协方差矩阵Q和R，则可根据数据段ab及式(11)～式(15)对b处系统状态进行估计。

2.2 模型参数辨识

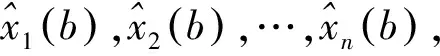
(21)

以b为起始点，对bc段对应的系统进行仿真，仿真输入为系统实际输入，仿真离散方程为：

(22)

将系统输出与仿真输出偏差的平方和作为智能寻优算法的适应度函数：

(23)

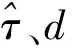
2.3 模型验证

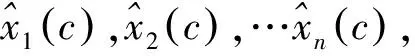
(24)

根据式(24)及寻优所得模型对cd段数据进行仿真，模型验证过程的系统离散方程为：

(25)

仿真过程中，仿真输入与cd段对应的实际输入一致，比较仿真输出与实际输出，从而完成模型的验证环节。

3 应用实例

高温过热器惰性区模型为带有较长纯迟延环节的高阶惯性对象，对其进行建模存在一定困难[16]，由于许多火电机组投入自动发电控制(AGC)的“R”模式负荷波动较为频繁，且绝大多数电厂均开展小指标竞赛，使得运行人员频繁调节减温水量，以保证在允许温度范围内尽可能地提高主汽温，这使得获取主汽温的稳定工况极为困难，因此，常规历史数据建模方法[10-12]不适用于高温过热器惰性区对象的模型辨识。该惰性区模型具有非线性特性，一般采用分段线性化的方式解决其非线性问题[3]。为简要说明本文方法的实用性，对某600 MW火电机组在300 MW稳定工况下的高温过热器惰性区模型进行辨识，其他工况建模方法与该工况相同。选取高温过热器的入口温度和出口温度作为建模数据，选取2 000组输入数据，为保证输出数据平移后，仍有足够多的输出数据与输入对应，输出数据选取2 500组，采样周期均为1 s，建模所选原始数据曲线见图3。

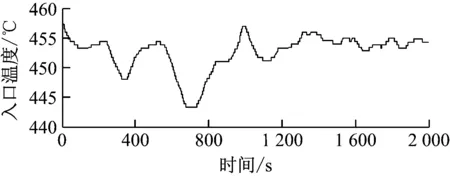
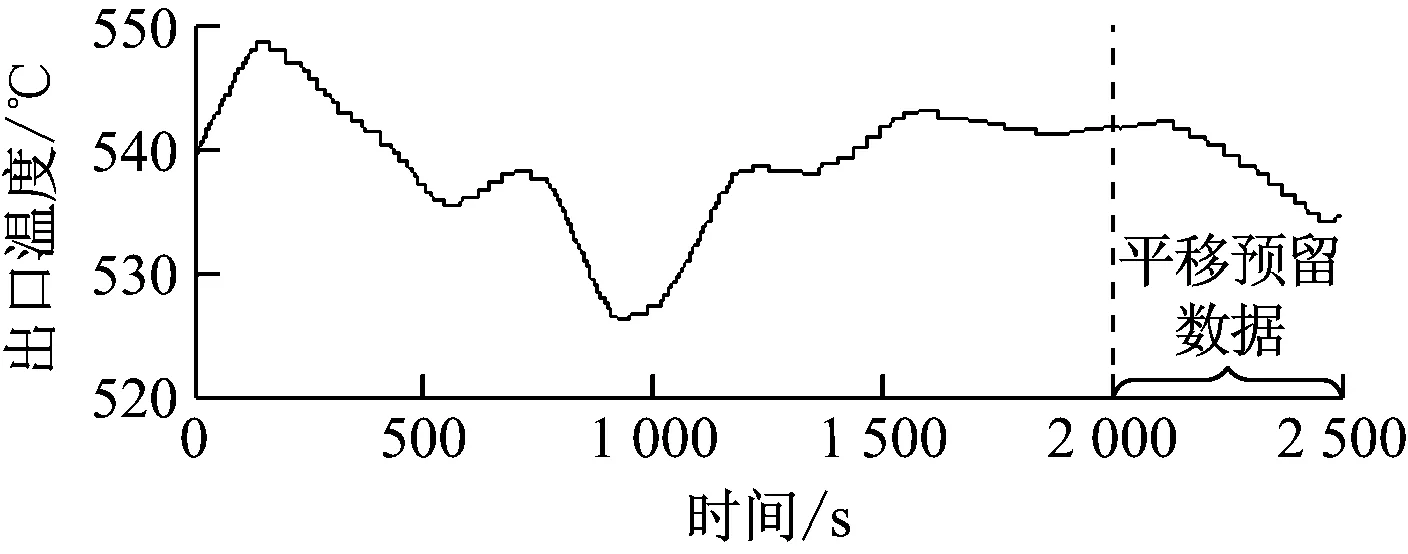
图3 高温过热器惰性区对象历史数据曲线

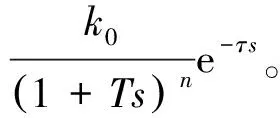
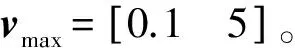
(26)

状态跟踪步数为600步。辨识结果曲线如图4所示。

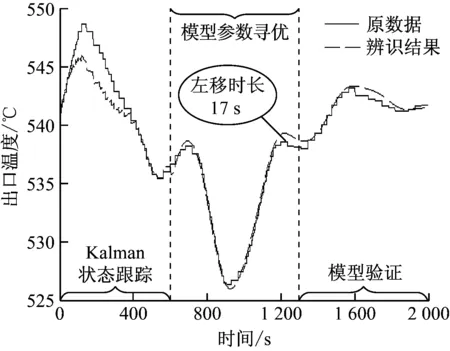
图4 高温过热器惰性区辨识结果

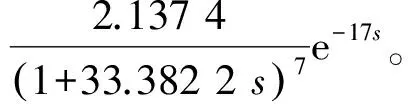
需要说明的是，为简要介绍该建模方法的有效性，此处选取了一定约束条件下的单入单出热工过程作为建模对象，对于许多热工过程而言，系统输入不唯一，因此，就需要选用被行业所公认的系统输出影响因素作为系统输入，选取对应的动态历史数据作为建模数据，依据预估纯迟延时间对输出数据进行平移，并依据d处各个系统输入的稳态分量及预估输出稳态分量对数据进行处理。另外，热工系统的输入个数改变后只需根据需要改变对应的A、B、H即可，仍可应用本文方法进行模型辨识。

此外，辨识所采用的历史数据采样周期应保证采样点基本复现真实数据的变化趋势，采样周期可根据对象性质选取，对于惯性大、阶次高的慢对象而言，可选取较大的采样周期，反之选取较小的采样周期。对于热工对象而言，历史数据库中存储的各系统数据均可满足建模要求。

4 结 论

(1) 提出一种基于迟延估计与Kalman状态跟踪的热工过程动态数据驱动建模方法。选取系统的动态历史数据作为建模数据，并将热工对象的纯迟延时间及输出的稳态分量作为寻优变量的2个维度与模型参数一起参与寻优过程。

(2) 应用热工对象的动态历史数据作为建模数据，不会对系统运行产生不利影响，且无需在海量历史数据中寻找系统稳态数据，大大降低了寻找可用建模数据的工作量。

(3) 与常规历史数据建模方法仅对智能寻优算法进行改进不同，本文方法同时从数据选取、建模数据处理以及建模方法设计3个角度出发，设计历史数据驱动建模方法，较好地契合了工业系统大数据建模的要求，为工业系统大数据建模的实现与推广提供了一种较好的参考方法。

[1] 秦志明, 张栾英, 谷俊杰. 直流锅炉单元机组协调控制系统的研究与设计[J].动力工程学报, 2016, 36(1): 16-21, 29.

QIN Zhiming, ZHANG Luanying, GU Junjie. Research and design on the coordinate control system of a once-through boiler unit[J].JournalofChineseSocietyofPowerEngineering, 2016, 36(1): 16-21, 29.

[2] 秦志明, 刘吉臻, 张栾英, 等. 直流炉机组简化非线性动态模型[J].动力工程学报, 2013, 33(12): 955-961.

QIN Zhiming, LIU Jizhen, ZHANG Luanying, et al. A simplified nonlinear dynamic model for once-through boiler units[J].JournalofChineseSocietyofPowerEngineering, 2013, 33(12): 955-961.

[3] 范永胜, 徐治皋, 陈来九. 基于动态特性机理分析的锅炉过热汽温自适应模糊控制系统研究[J].中国电机工程学报, 1997, 17(1): 23-28.

FAN Yongsheng, XU Zhigao, CHEN Laijiu. Study of adaptive fuzzy control of boiler superheated steam temperature based on dynamic mechanism analysis[J].ProceedingsoftheCSEE, 1997, 17(1): 23-28.

[4] SIMANI S, FANTUZZI C. Dynamic system identification and model-based fault diagnosis of an industrial gas turbine prototype[J].Mechatronics, 2006, 16(6): 341-363.

[5] 王新, 吕剑虹, 向文国. 一种改进的子空间辨识方法在热工过程中的应用[J].中国电机工程学报, 2010, 30(32): 96-102.

WANG Xin, LÜ Jianhong, XIANG Wenguo. A modified subspace identification method and its application in thermal process[J].ProceedingsoftheCSEE, 2010, 30(32): 96-102.

[6] LIU X J, KONG X B, HOU G L, et al. Modeling of a 1 000 MW power plant ultra super-critical boiler system using fuzzy-neural network methods[J].EnergyConversionandManagement, 2013, 65: 518-527.

[7] 曲亚鑫, 曾水平, 万常翔. 基于能量平衡原理的锅炉再热汽温反向建模[J].仪器仪表学报, 2013, 34(1): 38-44.

QU Yaxin, ZENG Shuiping, WAN Changxiang. Reversed modeling of boiler reheat steam temperature based on energy balance[J].ChineseJournalofScientificInstrument, 2013, 34(1): 38-44.

[8] 秦天牧, 刘吉臻, 方连航, 等. 基于改进偏互信息的火电厂SCR脱硝系统建模[J].动力工程学报, 2016, 36(9): 726-731, 738.

QIN Tianmu, LIU Jizhen, FANG Lianhang, et al. Modeling of power plant SCR denitrification system based on improved partial mutual information method[J].JournalofChineseSocietyofPowerEngineering, 2016, 36(9): 726-731, 738.

[9] 韩璞, 董泽, 王东风, 等. 智能控制理论及应用[M]. 北京: 中国电力出版社, 2013.

[10] 袁世通. 1 000 MW超超临界机组建模理论与方法的研究[D]. 北京: 华北电力大学, 2015.

[11] 袁世通, 韩璞, 孙明. 基于大数据的多变量系统建模方法研究[J].系统仿真学报, 2014, 26(7): 1454-1459, 1510.

YUAN Shitong, HAN Pu, SUN Ming. Modeling research of multivariable system based on big data[J].JournalofSystemSimulation, 2014, 26(7): 1454-1459, 1510.

[12] 韩璞, 袁世通. 基于大数据和双量子粒子群算法的多变量系统辨识[J].中国电机工程学报, 2014, 34(32): 5779-5787.

HAN Pu, YUAN Shitong. Multivariable system identification based on double quantum particle swarm optimization and big data[J].ProceedingsoftheCSEE, 2014, 34(32): 5779-5787.

[13] 王万召, 王杰. 采用限定记忆极限学习机的过热汽温逆建模研究[J].西安交通大学学报, 2014, 48(2): 32-37.

WANG Wanzhao, WANG Jie. Inverse modeling for superheated steam temperature based on restricted memory extreme learning machine[J].JournalofXi'anJiaotongUniversity, 2014, 48(2): 32-37.

[14] 彭丁聪. 卡尔曼滤波的基本原理及应用[J].软件导刊, 2009, 8(11): 32-34.

PENG Dingcong. Basic principle and application of Kalman filter[J].SoftwareGuide, 2009, 8(11): 32-34.

[15] 翁思义, 杨平. 自动控制原理[M]. 北京: 中国电力出版社, 2001: 353-355.

[16] 刘吉臻, 朱红路, 常太华, 等. 基于最小均方自适应滤波器的热工过程建模方法[J].中国电机工程学报, 2010, 30(5): 107-112.

LIU Jizhen, ZHU Honglu, CHANG Taihua, et al. Modelling method of thermal process based on least mean square adaptive filter[J].ProceedingsoftheCSEE, 2010, 30(5): 107-112.

[17] 黄宇, 韩璞, 李永玲. 主汽温系统模糊自适应内模控制[J].中国电机工程学报, 2008, 28(23): 93-98.

HUANG Yu, HAN Pu, LI Yongling. Fuzzy adaptive internal model control in main steam temperature system[J].ProceedingsoftheCSEE, 2008, 28(23): 93-98.