渐进一致φ-伪压缩型映象不动点的迭代逼近

隆建军

1 引言及预备知识

近些年，Mann迭代序列和Ishikawa迭代序列的迭代逼近已被许多学者研究[1-6]，利用其解决了许多类非线性算子方程解的问题.本文在赋范空间中分析了渐进一致φ-压缩型映象的Ishikawa及Mann迭代序列的收敛性及强收敛于渐进一致φ-压缩型映象不动点的条件.本文结果推广了现有文献[1,7,8,9,10,11]中的结果.

设X是一个实赋范线性空间，X*是X的对偶空间，<●，●>表示X*与X间的广义对偶对，映象J:X→2X*是由下式定义的正规对偶映象：

定义1设D是X的一个非空子集，T:D→D是一个映象，φ：[0,+∞）→[0,+∞）是一严格增加的函数，满足 φ（0）=0.

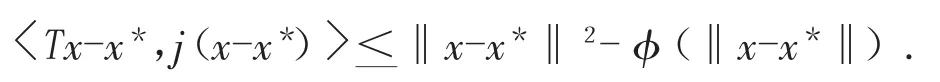
（4）T称为渐进一致φ-伪压缩：

定义2设D是X的一个非空子集，T：D→D称为一致L-Lipschitz映象：

引理 1［12］设 X 是一个实赋范空间,是正规对偶映象，则有

2 主要结论及其证明

定理1设D是赋范空间X的一个非空凸子集，T:D→D是渐进一致φ-伪压缩的一致L-Lipschitz映象，则

(1)若q∈D是T的任一不动点，则q=x*，从而T至多只有一个不动点；

(2)若T(D)是X中的有界集，且Аx0∈D，Ishikawa迭代序列｛xn｝定义如下：

其中｛αn｝，｛βn｝是[0,1]中的实数列，｛mn｝，｛kn｝是任意两个正整数列，且满足以下条件：

则｛xn｝强收敛于T的不动点x*，特别地，若q∈D是T的不动点，则

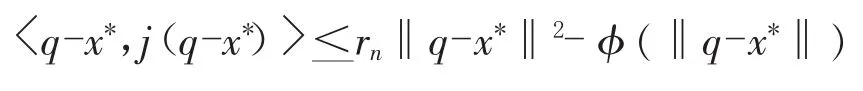
又由j是正规对偶映象，所以=‖q-x*‖2，故

即 φ（‖q-x*‖）＜（rn-1）‖q-x*‖2,n＞1

令n→∞，则有φ（‖q-x*‖）＜0，再由φ的性质即得q=x*.

由于T（D）是X中的有界集，我们定义

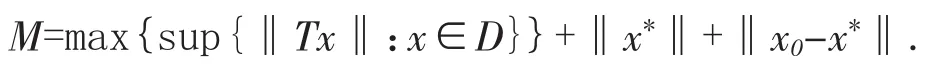
下证

事实上当n＝0时，有

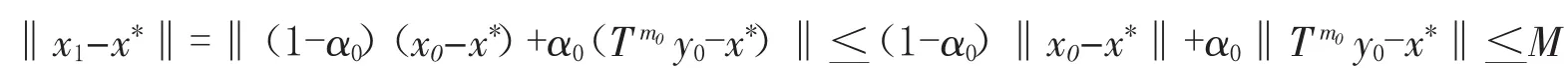
设当n＝k-1,k＞1时，结论成立，则当n＝k时，有

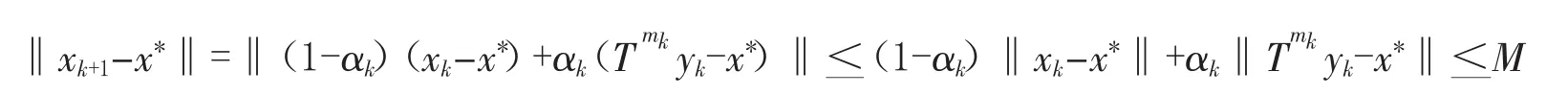
故由归纳法原理知，(2.2)式对一切n＞0都成立.

另外，由引理1、(2.1)、(2.2)及是一致L-Lipschitz映象可得，

由(2.2)知｛xn｝有界，再由 T（D）有界及条件(Ⅱ)可得

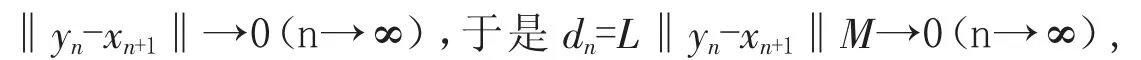
将(2.4)代入(2.3)中可得

即有

由 αn→0，rmn→0（n→0）知，∈N+当 n＞n0时，1-2αnrmn＞0，于是当 n＞n0时，有

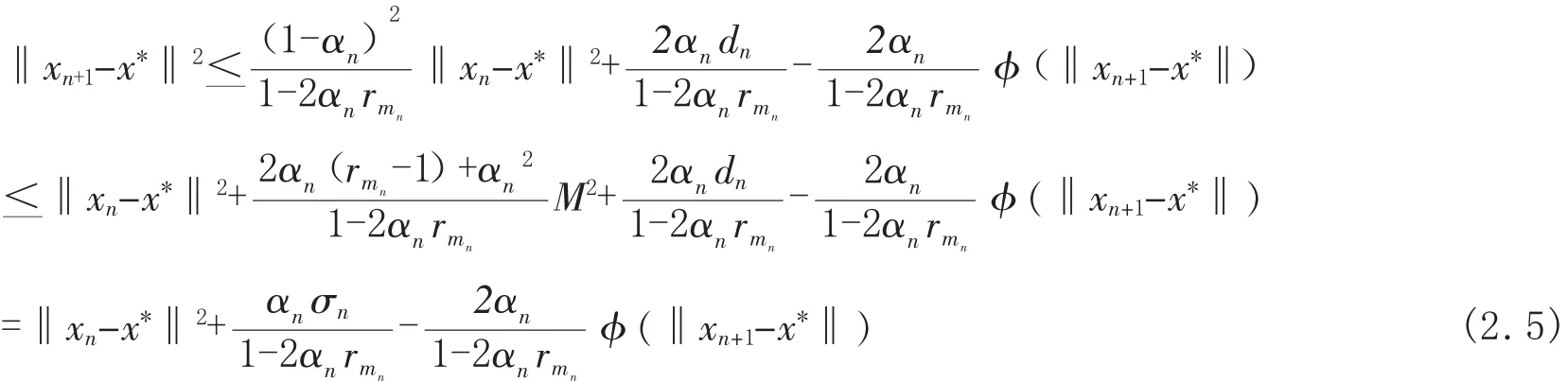
其中 σn=2αn（rmn-1）M2+2dn→0（n→∞）.

设 δ=inf｛‖xn+1-x*‖：n＞0｝，则 δ＞0，下证 δ=0

假设δ＞0，则‖xn+1-x*‖＞δ，Аn＞0，从φ的严格增加性质可得

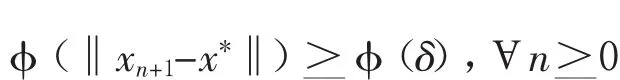
于是由(2.5)式，有

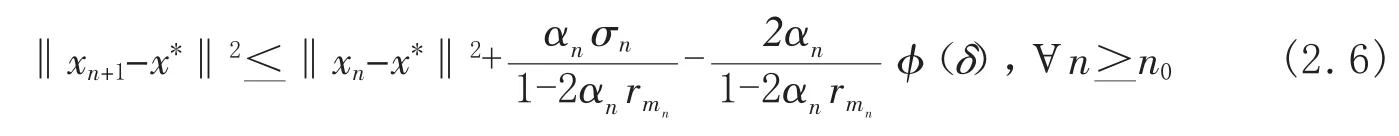
又由 σn→0（n→∞），所以 n＞n0，使得 σn＜φ（δ），n＞N，于是从(2.6)，可得

即 αnφ（δ）＜‖xn-x*‖2-‖xn+1-x*‖2，＞N.对此式求和得

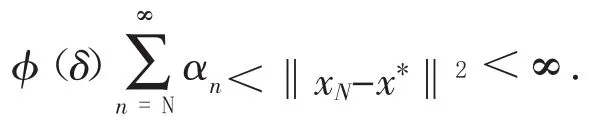
此与(Ⅲ)相矛盾，故必有 δ=0，即 δ=inf｛‖xn+1-x*‖：n＞0｝=0.因此

事实上，由(2.7)知i=1时，结论成立，对于i=2时，假设‖xnj+2-x*‖＞ε，则由φ的严格增加性可得‖xnj+2-x*‖＞φ（ε）＞0，从而由(2.5)和(2.7)有

此与假设‖xnj+1-x*‖＞ε相矛盾，故必有‖xnj+2-x*‖＜ε，由数学归纳法，可证得(2.8)式对一切i＞0成立，由ε＞0的任意性，有至此定理得证.

定理2设D是赋范空间X的一个非空凸子集，T:D→D是渐进一致φ-伪压缩的一致L-Lipschitz映象，则

(1)若q∈D是T的任一不动点，则q=x*，从而T至多只有一个不动点；

(2)若T（D）是X中的有界集，且Аx0∈D,Mann迭代序列｛xn｝定义如下：

其中｛αn｝是[0，1]中的实数列，｛mn｝是任意正整数序列，且满足以下条件：

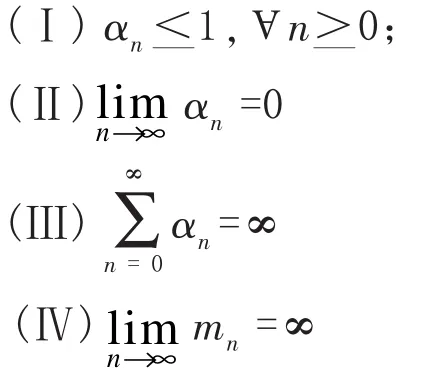
则｛xn｝强收敛于T的不动点x*，特别地，若q∈D是T的不动点，则

证明：在定理1中，令 βn=0（n＞0），即得定理2.

[1]吴婷.广义渐近拟非扩张映射不动点的收敛性[J].四川理工学院学报(自然科学版)，2007,20(6)：27-31.

[2]杨丽.具非扩张映象的修改Ishikawa迭代序列的C KQ方法[J].四川理工学院学报(自然科学版)，2008,21(1)：19-21.

[3]吴婷.凸度量空间内广义渐近拟非扩张映射不动点的迭代[J].四川理工学院学报(自然科学版)，2008,21(2)：44-47.

[4]李柳芬.不动点、压缩映射原理的进一步研究[J].四川理工学院学报(自然科学版)，2008,21(3)：9-11.

[5]兰恒友，李作安.Banach空间中一类隐式微分方程的含误差的Ishikawa迭代[J].四川理工学院学报(自然科学版)，2002,15(3)：6-11.

[6]田有先.凸度量空间拟非线性扩张映射不动点的Ishikawa迭代[J].四川理工学院学报(自然科学版)，2002,15(4)：1-3.

[7]陈汝栋，姚永红.一致φ-伪压缩映象不动点的迭代逼近[J].应用泛函分析学报，2004,6(3):93-96.

[8]Chang S S,Tan K K.Iteration processes for approximation fixed point of operators of monotone type[J].Bull Austral Math Soc,1998,57:433-445.

[9]彭再云，龙宪军，王其林.Banach空间中关于一致Lipschit z ian映象的一个新结果[J].重庆师范大学学报（自然科学版），2009,26(3):5-7.

[10]张芳，向长合.一致L-Lipschit z的渐近伪压缩非自映象不动点的迭代逼近[J].重庆师范大学学报（自然科学版），2009,26(1):7-10.

[11]龙宪军，彭再云，敖军.关于Lipschitzian严格伪压缩映象的带误差的Ishikawa型迭代程序[J].重庆师范大学学报（自然科学版），2009,26(2):7-11.

[12]Zhou H Y,Cho Y J.Ishikawa and Mann iterative processes with errors for nonlinear strongly quasi-accretive map ping in normedlinear space[J].J Korean Math Soc,1999,36(6):1031-1037.