海洋湍流中自适应光学成像系统特征参量研究∗

吴彤 季小玲 罗燏娟

(四川师范大学物理与电子工程学院,成都 610068)

(2017年8月16日收到;2017年11月26日收到修改稿)

1 引 言

自适应光学(adaptive optics,AO)的概念和原理最早于1953年由海尔天文台的Horace Babcock提出,直到20世纪70年代这一设想才得以实现,其主要用于实时校正光束波前畸变,以提高光学系统成像性能.目前,AO技术已广泛被应用于天文观测、激光传输、人眼成像、生物医学等领域[1−4].Strehl比、Greenwood时间常数和等晕角等是自适应光学成像系统特征参量[5].Strehl比表征由于非理想因素使得光强峰值下降的程度[6],Greenwood时间常数表征有效校正因湍流引起的波前畸变所需的系统波前探测器采样的最短时间[7],等晕角表征湍流引起的波前畸变得到补偿的两个测量点间对同一观察目标能保持相位相干的最大角度[8].迄今为止,国内外学者已对大气湍流中自适应光学成像系统这三个特征参量做了大量研究[9−15].例如:2004年,Fusco和Conan[9]研究了AO系统沿轴和离轴方向上短曝光斯特列尔比的统计行为,给出了沿轴方向上短曝光斯特列尔比统计量的表达式.1977年,Greenwood[10]提出了大气湍流中Greenwood时间常数的相关理论;2015年,瞿青等[11]利用位相差值法实现了大气湍流Greenwood时间常数的测量.1979年,Loos和 Hogge[12]提出了大气湍流等晕角的相关理论,该理论已被广泛应用[13−15],但传统的自适应光学系统只能在很小的视场内进行高精度成像.为了能在更大范围获得清晰的像,可采用多层共扼自适应光学扩大等晕角,提高成像质量.2008年,Ding等[13]研究了大气湍流中激光雷达中的双层共扼系统;2014年和2015年,Yu等[14,15]分别从理论和实验上证明了可以利用球面波闪烁测量有限距离内的等晕角.

随着水下光通信、传感和激光雷达等应用的兴起,水下环境对光成像提出了新的挑战.已有实验证明:自然环境中水下湍流是限制成像质量的一个重要因素[16].2012年,美国海军研究实验室Hou等[17]通过测量自然水域中湍流耗散率,用调制传递函数定量地描述图像质量劣化程度.与大气湍流不同,海洋湍流是由温度和盐度变化引起水折射率起伏而造成的,其折射率起伏空间功率谱具有复杂的双峰值结构.Nikishov等[18]建立了海洋湍流折射率起伏空间功率谱的解析模型.最近,我们课题组推导出了海洋湍流中光波空间相干长度和可见参数的解析表达式,并修正了Hou等[19,20]提出的水下光学成像模型.然而,迄今为止海洋湍流中自适应光学成像系统特征参量Strehl比、Greenwood时间常数和等晕角的研究还未涉及.本文拟推导出海洋湍流中这三个特征参量的解析表达式,并研究海洋湍流对这三个特征参量的影响.

2 Strehl比

在各向同性的均匀海水介质中,Nikishov等[18]建立了海洋湍流折射率起伏空间功率谱的解析模型,即:

其中κ是空间波数,η是Kolmogorov内尺度,AT=1.863×10−2,AS=1.9×10−4,ATS=9.41×10−3,δ=8.284(κη)4/3+12.978(κη)2,ε表示海水单位质量湍流动能耗散率,其取值范围为10−1—10−10m2/s3,χT表示海水温度方差耗散率,其取值范围为10−4—10−10K2/s,ω表示海洋湍流功率谱中温度与盐度起伏引起折射率变化贡献的比率,其范围取值为[−5,0],−5和0分别对应于温度和盐度变化引起的光学湍流.值得指出的是,Nikishov等建立的海洋湍流折射率起伏空间功率谱模型在弱、中、强海洋湍流中均可适用[18,21].该模型是基于Hill提出的温度起伏以及盐度起伏的标量谱模型建立的,而Hill[22,23]模型有大量实验数据验证其正确性.目前,Nikishov等建立的海洋湍流折射率起伏空间功率谱模型已被广泛利用[24−28].

基于Nikishov等提出的海洋湍流功率谱,2016年我们课题组推导出了海洋湍流中球面波可见参数r0的解析表达式[20]:

其中L为传输距离,波数k=2π/λ,λ为波长.

Strehl比(SR)是评价光学系统成像质量好坏的重要物理量,它表示焦平面上的实际光波光强峰值与理想光波光强峰值之比[5].长曝光Strehl比SRLE的精确解析解很难求得,但采用内插值方法可给出代数形式的近似解[5]:

其中LE表示长曝光,DG为光学系统的光瞳直径.

短曝光Strehl比SRSE的精确解析解也很难求得,本文采用内插值方法求其代数形式的近似解.由调制传递函数MTF表示的SRSE的积分形式如下[5]:

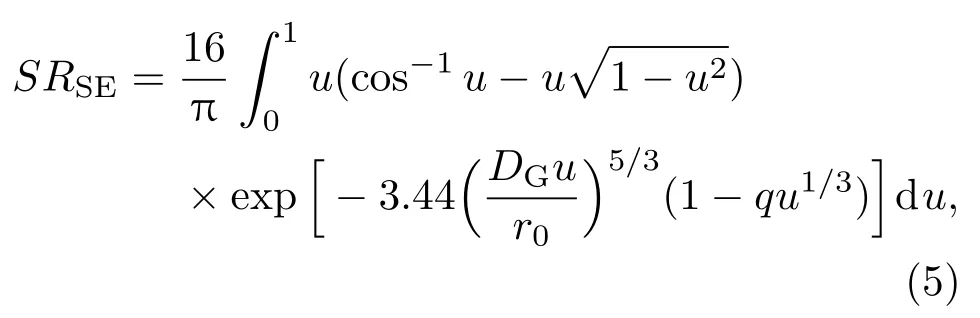
其中q为表征MTFSE远场与近场参数.近场条件下,q=1;远场条件下,q=0.5.相比于长曝光成像,短曝光成像应除去因大尺度倾斜效应所引起的像斑随机位移部分,则短曝光Strehl比的代数近似解应从长曝光Strehl比(3)式中合理地去除含有因子(DG/r0)5/3的到达角起伏项.因此,SRSE的代数近似式可写为:

其中y(q)为与参数q有关的调节系数,其表达式为[29]

为验证本文所得(6)式的正确性,将分别讨论DG/r0≫1和DG/r0≪1两种极限情况下(6)式与(5)式的一致性.当满足DG/r0≫1时,只考虑短曝光时湍流MTFSE的影响,忽略透镜MTF0的影响[30],(5)式可简化为

其中H=3.44(λ/r0)5/3.比较(8)式与DG/r0≫1时的(6)式可知,两者是一致的.

当满足DG/r0≪1时,只考虑透镜MTF0的影响,忽略短曝光时湍流MTFSE的影响[20],并利用贝塔函数B(P,Q),对(5)式做积分变换,(5)式可简化为

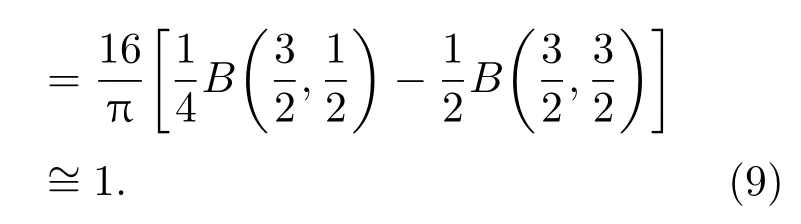
比较(9)式与(6)式(当DG/r0≪1时)可知,两者也是一致的.

另一方面,本文还利用数值计算结果验证了(6)式的正确性(见图1和图2).由图1和图2可知:仅在DG/r0=1附近,SRSE的代数近似式(6)与(5)式存在差异,其他区域两者均符合得很好.SRSE的代数近似式(6)式在近场的误差大于远场的误差,例如:近场最大相对误差接近16%,而远场最大相对误差小于5%.因此,除了在近场DG/r0=1附近外,本文所得SRSE的代数近似式(6)式在弱湍流情况下均可保证足够的精度.

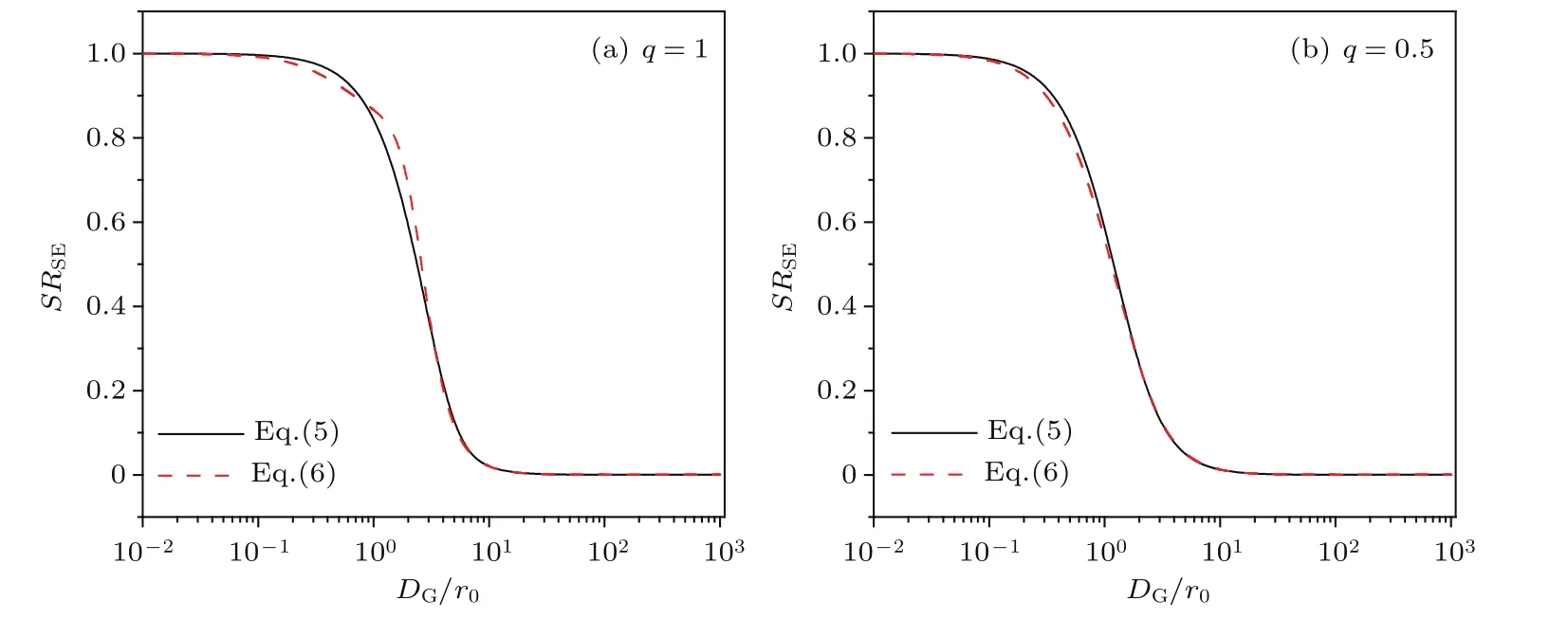
图1 短曝光Strhel比SRSE随DG/r0的变化 (a)近场;(b)远场Fig.1.Curves of SRSEversus DG/r0:(a)Near field;(b)far field.

图2 近似(6)式与积分(5)式的相对误差Δ随DG/r0的变化 (a)近场;(b)远场Fig.2.Curves of the relative error Δ between Eq.(6)and Eq.(5)versus DG/r0:(a)Near field;(b)far field.

根据本文所得SRSE的近似公式(6),可以研究海洋湍流各参数(ω,ε,χT)对短曝光时的SRSE的影响(见图3).图3中同时还给出了长曝光时SRLE曲线,若图中没有特别标注,计算参数为:光波波长λ=0.532µm,光瞳直径DG=0.3 m,传输距离L=9 m,q=1,ω=−3,ε=10−6m2/s3,χT=10−8K2/s.根据计算参数可知:图3考虑的是近场情况,但不在DG/r0=1附近,因此计算结果是可信的.图3(a)表明:随着ω的增大(即盐度变化引起的海洋湍流逐渐占主导地位),长、短曝光的Strehl比均减小,即系统的成像质量变差.并且,随着海水湍流动能耗散率ε的减小(见图3(b))或海水温度方差耗散率χT的增大(见图3(c)),长、短曝光的Strehl比均减小,即成像质量变差.从图3还可看出SRSE＞SRLE,这是因为短曝光成像SRSE中除去了因大尺度倾斜效应而引起的到达角起伏项.此外,远场情况下也可得到与近场情况类似的结果,本文不再赘述.

海洋湍流中,短曝光成像的Strehl比SRSE随传输距离L变化曲线示于图4,若图中没有特别标注,计算参数为:q=1,ω=−3,ε=10−6m2/s3,χT=10−8K2/s,λ=0.532 µm,DG=0.3 m.可以看出:随着L和DG的增大(图4(a))及λ的减小(图4(b)),SRSE减小,即系统成像质量变差.

图3 Strehl比SR随海洋湍流各参数的变化 (a)ω;(b)ε;(c)χTFig.3.Curves of Strehl ratio versus the oceanic turbulence parameters:(a)ω;(b)ε;(c)χT.

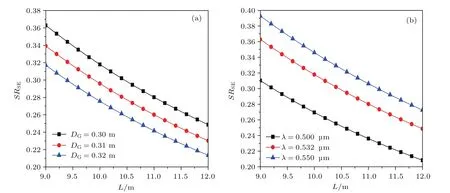
图4 海洋湍流中,短曝光Strehl比SRSE随L的变化Fig.4.Curves of short-exposure Strehl ratio versus L in oceanic turbulence.

3 Greenwood时间常数

Greenwood时间常数τ0是指湍流基本保持不变的时间间隔[5].τ0越大,表征湍流扰动越弱,反之湍流扰动越强[7].大气湍流中Greenwood时间常数可表示为[31]

最近,Baykal推导出了弱海洋湍流情况下球面波等效折射率结构常数[32],

其中Φn(κ)为Nikishov提出的海洋湍流功率谱.

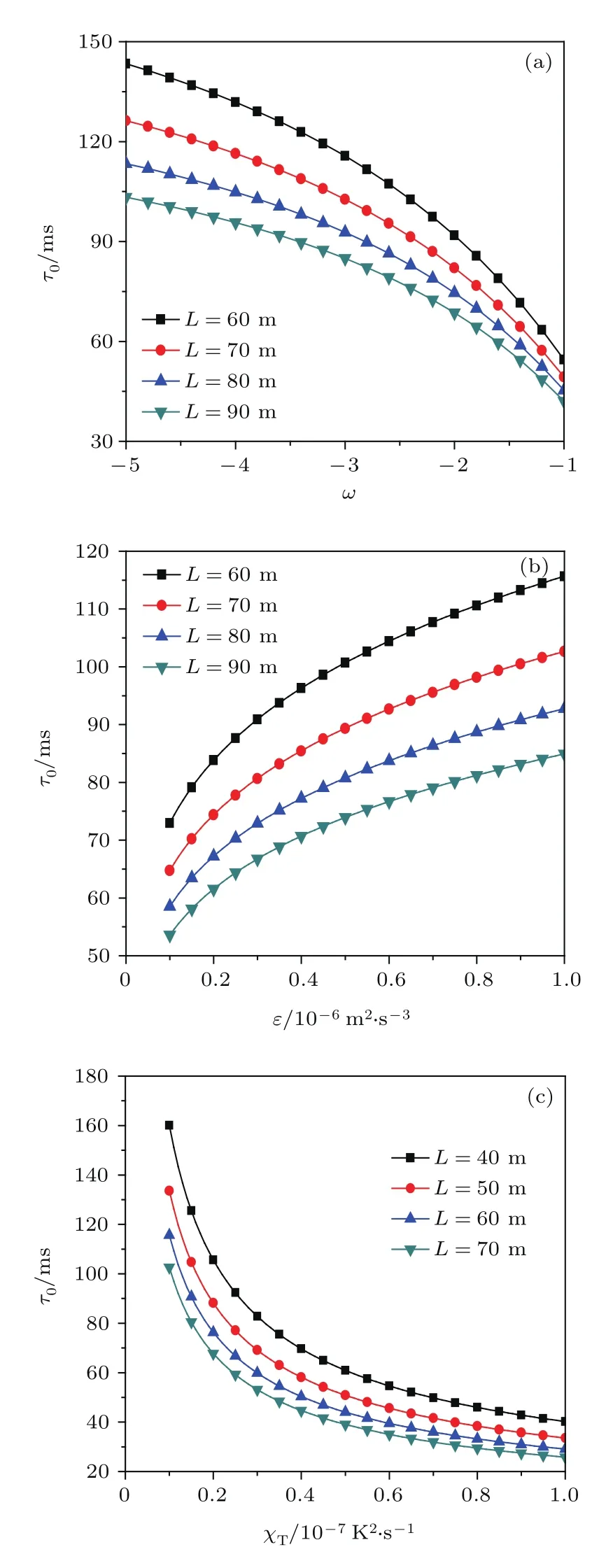
图5 Greenwood时间常数τ0随海洋湍流参数的变化(a)ω;(b)ε;(c)χTFig.5.Curves of Greenwood time constant τ0versus oceanic turbulence parameters:(a)ω;(b)ε;(c)χT.

将(11)式代入(10)式中,且考虑横向海水流速为常数v,即可化简得到弱海洋湍流情况下海洋湍流Greenwood时间常数为

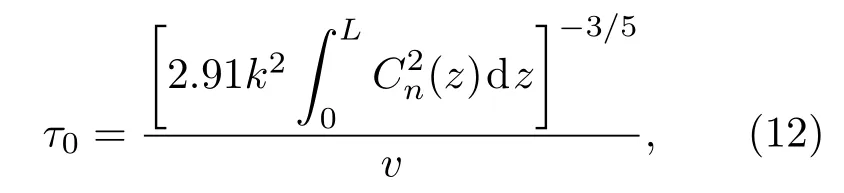
(12)式仅对于海洋湍流参数不随传输路径变化情况有效.

海洋湍流中,Greenwood时间常数τ0随海洋湍流各参数(ω,ε,χT)变化曲线示于图5,若图中没有特别标注,计算参数为:Kolmogorov内尺度η=1 mm,波长λ=0.532µm,海水横向流速v=0.04 m/s,ω=−3,ε=10−6m2/s3,χT=10−8K2/s. 图5表明,Greenwood时间常数τ0随ω,χT的增大及ε的减小而减小,即湍流保持不变的时间τ0减小.此外,传输距离L越远,对应的τ0也越小.为了有效校正因湍流引起的波前畸变,系统波前探测器的采样时间应小于τ0,否则会导致测量值有较大误差.因此可根据实际海洋湍流参数得到对应的τ0值来调节自适应光学系统的采样时间,提高系统的校正精度.

4 等晕角

等晕角是描述光波在湍流中传播时两点间角度相干性的物理量,是自适应光学系统的重要参数之一.等晕角值为两个测量点间对同一观察目标能保持相位相干的最大角度,若大于这个最大角度,则湍流引起的波前畸变将无法得到补偿[8].依据文献[12]中等晕角的定义,在各向同性且均匀的海水介质中的等晕角可表示为

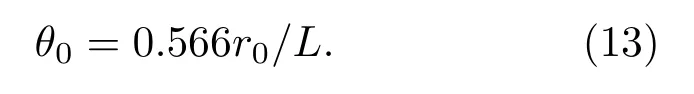
将海洋湍流中可见参数r0表达式(2)代入(13)式中,即可得海洋湍流中球面波等晕角的解析表达式,

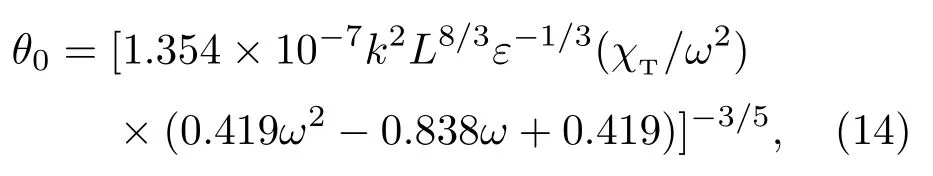
等晕角(14)式在弱、中、强海洋湍流条件下均成立.

海洋湍流中,等晕角θ0随海洋湍流各参数(ω,ε,χT)变化曲线示于图6,若图中没有特别标注,计算参数为:λ=0.532µm,ω=−3,ε=10−6m2/s3,χT=10−7K2/s.图6表明,随着ω,χT的增大以及ε的减小,等晕角θ0减小,即系统可校正湍流的角度范围减小,光波的波前畸变便无法得到适当补偿.此外,传输距离增加,θ0也明显减小.值得指出的是,海洋湍流对系统的视场角度影响很大,例如:海洋湍流中光短距离传输(如100 m)后,等晕角可下降至微弧度量级,这与大气湍流中光从地面到太空近垂直路径长距离传输时等晕角的数量级相同.

图6 等晕角θ0随海洋湍流参数的变化 (a)ω;(b)ε;(c)χTFig.6. Curves of isoplanatic angle θ0versus the oceanic turbulence parameters:(a)ω;(b)ε;(c)χT.

5 结 论

本文研究了海洋湍流对自适应光学成像系统三个特征参量(即Strhel比SR,Greenwood时间常数τ0和等晕角θ0)的影响.推导出了海洋湍流中短曝光成像Strhel比SRSE的代数近似解析表达式,并证明:除了在近场DG/r0=1附近外,本文所得SRSE的近似公式均可保证足够的精度.此外,还得到了海洋湍流中Greenwood时间常数τ0和等晕角θ0的解析表达式.研究表明:随着盐度变化引起的海洋湍流逐渐占主导地位(即海洋湍流功率谱中温度与盐度的比率ω的增大),SR,τ0和θ0值均减小;随着海水湍流动能耗散率ε的减小或海水温度方差耗散率χT的增大,SR,τ0和θ0值亦均减小.SR,τ0和θ0值减小意味着成像质量变差、波前探测器的采样时间减小、系统可校正湍流的角度范围变小.下面从描述海洋湍流的三个主要参数的物理含义来解释本文结果.第一,海水单位质量湍流动能耗散率ε,它由黏滞力引起,将湍流动能转换成分子热运动的动能.第二,海水温度方差耗散率χT,较大的χT表示湍流具有较强能量.第三,温度与盐度起伏引起折射率变化贡献的比率ω,而盐度起伏占主导地位时比温度起伏占主导地位引起的光学湍流更严重[18,22].因此,χT和ω值越大、ε值越小,表明海洋湍流越强,则SR,τ0和θ0值越小.

值得指出的是,大气湍流中,光从地面到太空近垂直路径长距离传输时,典型等晕角度值达微弧度量级[5].然而,本文研究表明,海洋湍流中光在短距离传输(如100 m)等晕角可下降至微弧度量级.可见,海洋湍流对等晕角影响很大.本文研究结果对工作于水下湍流环境中自适应光学成像系统应用具有理论参考作用.

[1]Guo Y M,Rao C H,Bao H,Zhang A,Wei K 2014Acta Phys.Sin.63 149501(in Chinese)[郭友明,饶长辉,鲍华,张昂,魏凯2014物理学报63 149501]

[2]Booth M J 2014Light-Sci.Appl.3 e165

[3]Miller D T,Kocaoglu O P,Wang Q,Lee S 2011Eye25 321

[4]Jiang W H 2006Chin.J.Nature28 7(in Chinese)[姜文汉2006自然杂志28 7]

[5]Andrews L C,Phillips R L 2005Laser Beam Propagation through Random Media(2nd Ed.)(Bellingham,WA:SPIE Optical Engineering Press)pp606–623

[6]Mahajan V N 2005J.Opt.Soc.Am.A22 1824

[7]Chen T J,Zhou W C,Wang F,Huang D Q,Lu Y H,Zhang J Z 2015Acta Phys.Sin.64 134207(in Chinese)[陈天江,周文超,王峰,黄德权,鲁燕华,张建柱 2015物理学报64 134207]

[8]Zong F,Qiang X W,Wu M,Chang J Y,Feng S L 2014Acta Opt.Sin.34 16(in Chinese)[宗飞,强希文,吴敏,常金勇,封双连2014光学学报34 16]

[9]Fusco T,Conan J M 2004J.Opt.Soc.Am.A21 1277

[10]Greenwood D P 1977J.Opt.Soc.Am.67 390

[11]Qu Q,Cao Z L,Hu L F,Zhang H S,Zhao J L,Xuan L 2015Chin.Opt.8 121(in Chinese)[瞿青,曹召良,胡立发,张红胜,赵晶丽,宣丽2015中国光学8 121]

[12]Loos G C,Hogge C B 1979Appl.Opt.18 2654

[13]Ding X K,Rong J,Bai H,Wang X,Shen J E,Li F 2008Chin.Opt.Lett.6 1

[14]Yu L K,Xu J,Hong S,Hou Z H,Yi W 2014Opt.Lett.39 789

[15]Yu L K,Hou Z H,Zhang S C,Xu J,Yi W 2015Opt.Eng.54 024105

[16]Bogucki D J,Domaradzki J A,Ecke R E,Truman C R 2004Appl.Opt.43 5662

[17]Hou W L,Woods S,Jarosz E,Goode W,Weidemann A 2012Appl.Opt.51 2678

[18]Nikishov V V,Nikishov V I 2000Int.J.Fluid Mech.Res.27 82

[19]Lu L,Ji X L,Baykal Y 2014Opt.Express22 027112

[20]Pu H,Ji X L 2016J.Opt.18 105704

[21]Lu W,Liu L,Sun J 2006J.Opt.A:Pure Appl.Opt.8 1052

[22]Hill R J 1978J.Fluid Mech.Res.88 541

[23]Hill R J 1978J.Opt.Soc.Amer.68 1067

[24]Korotkova O,Farwell N,Shchepakina E 2012Wave Random Complex22 260

[25]Tang M M,Zhao D M 2013Appl.Phys.B111 665

[26]Baykal Y 2016Opt.Commun.375 15

[27]Yang T,Ji X L,Li X Q 2015Acta Phys.Sin.64 204206(in Chinese)[杨婷,季小玲,李晓庆 2015物理学报 64 204206]

[28]Liu Y X,Chen Z Y,Pu J X 2017Acta Phys.Sin.66 124205(in Chinese)[刘永欣,陈子阳,蒲继雄2017物理学报66 124205]

[29]Ma X L 2015Acta Photon.Sin.44 0601003(in Chinese)[马雪莲 2015光子学报44 0601003]

[30]Fried D L 1966J.Opt.Soc.Am.56 1372

[31]Fried D L 1990J.Opt.Soc.Am.A7 1224

[32]Baykal Y 2016Appl.Opt.55 1228