一种具有隐藏吸引子的分数阶混沌系统的动力学分析及有限时间同步∗

郑广超 刘崇新 王琰

(西安交通大学电气工程学院,电力设备电气绝缘国家重点实验室,西安 710049)

(2017年10月31日收到;2017年11月23日收到修改稿)

1 引 言

自19世纪60年代Lorenz[1]首次提出混沌系统以来,发现了大量的三维混沌系统,如Rössler系统[2],Chen系统[3],Liu系统[4]以及其他一些典型三维混沌系统[5−8],这些混沌动力学系统在保密通信学、经济学、工程学等领域得到了广泛的应用.在混沌系统中,存在的吸引子一般分为两种,自激吸引子和隐藏吸引子.自激吸引子由不稳定的平衡点产生,而隐藏吸引子的吸引盆与任何不稳定的平衡点均不相交.长期以来,人们认为混沌系统的吸引子与其平衡点之间存在着密切的联系,混沌判定的定性准则也主要是通过Shilnikov定理[9]来进行,即混沌的产生至少需要一个不稳定的平衡点,同时这个不稳定的平衡点也对应着混沌系统中的一个吸引子.然而,自从Leonov和Kuznetsov[10]基于Chua系统发现隐藏吸引子以来,许多学者对具有隐藏吸引子的混沌系统产生了极大的兴趣,取得了很多成果[11−17].这些特殊的混沌系统仅有一个稳定平衡点[11,12],甚至没有平衡点[13,14]或者有无穷多平衡点[15],这对传统混沌判定的准则提出了新的挑战.此外,由于混沌吸引子不能用一般的数值分析方法来寻找,在一定程度上增加了混沌系统动力学行为的复杂性和不易预测性,这对于实际工程应用,尤其是保密通信领域有重要的理论研究价值.目前,对于具有隐藏吸引子的混沌系统的研究,既有文献大多是关于整数阶系统的研究,关于分数阶系统的研究相对较少.

分数阶微积分几乎与整数阶微积分有一样长的历史,但是由于缺乏实际工程应用背景,分数阶微积分的发展相对缓慢.直到近三十年来,人们发现用分数阶微积分描述复杂的系统时,其物理意义更清晰,表述更简洁,特别是当研究对象本身带有分数阶特性时,能更好地揭示对象的本质及其行为特性,由此分数阶微积分逐渐得到人们的重视,其在工程领域和物理方面的应用成为了研究的热点.长期以来,由于缺乏有效的数学工具来描述许多实际物理系统的无限记忆功能和遗传特性,几乎所有的系统都采用整数阶模型来描述,这在很大程度上忽略了系统的真实性.分数阶系统作为整数阶系统的推广,具有普遍意义,能更清晰地描述系统的物理特性,且具备特有的历史记忆功能.

随着对分数阶混沌系统的研究不断深入,人们认识到分数阶混沌系统的同步在保密通信和信息科学等领域的应用前景比整数阶混沌系统更加广泛[18].自从1990年美国海军实验室Pecora和Carroll[19]提出了混沌同步概念和方法以来,随着混沌同步研究的不断深入,混沌同步已成为混沌和控制领域的研究热点,许多有效的混沌同步控制方法相继被提出.然而,由于分数阶混沌系统实现同步的复杂性,相比整数阶系统,对分数阶混沌系统的同步控制的研究起步较晚.2003年,李春光等[20]通过数值仿真第一次实现了分数阶混沌系统的同步,这极大地激发了人们对分数阶混沌系统同步问题开展研究的兴趣,提出了更多实现分数阶混沌系统的同步方法[21−24].其中,针对分数阶混沌系统有限时间同步问题,赵灵冬等[24]提出了分数阶系统有限时间稳定性理论,实现了分数阶系统有限时间同步,且与完全同步对比效果十分显著.

基于以上研究,考虑将分数阶微积分推广到具有隐藏吸引子的系统中,并实现有限时间同步,这对混沌技术在实际工程领域的应用有重要的研究价值,尤其是在保密通信领域,可以实现更复杂的动力学行为,提高通信系统的安全度.

本文基于Sprott E系统,构建了一种仅有一个稳定平衡点的分数阶混沌系统,其在不同阶次下会处于周期、倍周期和混沌状态,分析了该系统的一些基本动力学行为,如平衡点、吸引子、Poincare映射和分岔等.另外,运用分数阶有限时间同步控制理论实现了同步控制并进行了数值仿真.

2 分数阶系统模型及动力学分析

2.1 分数阶微分概述

在分数阶微积分的研究过程中,对微分和积分概念提出了许多种定义[25],主要有Grunwald-Letnikov(G-L)定义、Riemann-Liouville(R-L)定义以及Caputo定义等,其中Riemann-Liouville定义和Caputo定义较为常用,Riemann-Liouville定义多用于纯数学领域中,Caputo定义更适用于工程应用领域,适合分数阶微分方程初始值问题的描述.

一般在实际应用中常用Caputo定义,且Caputo定义可取非同质的初始条件.本文采用Caputo分数阶微分定义.

定义1Caputo分数阶微分定义为

式中C表示此定义为Caputo分数阶微分定义,q为微分算子的阶次,n为大于q的最小整数,且n−1＜q＜n,t,a分别为运算的上下限,Γ(·)为Gamma函数.

Caputo分数阶微分相关的性质如下.

性质1[25]

考虑一般的分数阶微分方程可描述为

该方程的通解为

其中Mittag-Leffter函数为

2.2 系统模型及平衡点

SprottE系统最早是由美国学者J.C.Sprott[26]通过计算机穷举法发现的,由两个二次非线性项的五项多项式组成,是最简的三维混沌系统之一,其物理实现相对容易.Sprott E系统在平衡点处的特征根中有一对共轭的纯虚根,通过对系统加入小的扰动项,很容易使这对共轭的纯虚根转变成为一对具有负实部的共轭特征根,从而使系统具有稳定的特征根,且能够使系统的混沌特性保留下来.在实际应用中,混沌系统很容易受小干扰的影响而使特征根的性质发生变化,Sprott E系统便是符合这种情况的典型混沌系统之一.文献[12]基于Sprott E系统构建了一种具有一个稳定平衡点的整数阶混沌系统,并通过相轨迹图、时域图、李雅普诺夫指数图和频率谱进行了分析.本文在此基础上,将其推广到分数阶,构造一种含隐藏吸引子的新分数阶混沌系统:

式中q为系统((5)式)的阶次,且0＜q≤1,a为加入的系统参数,取a=0.005.

令(5)式右侧为0,得到系统的平衡点方程为

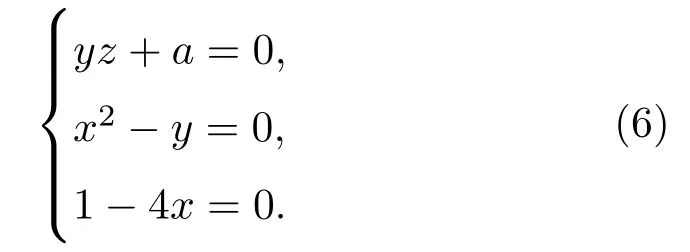
通过求解(6)式得到系统仅具有一个平衡点O(0.25,0.0625,−0.08).

在此平衡点O处,系统的雅可比矩阵为

令其特征多项式det(λI−J)=0,得到相应的特征值为

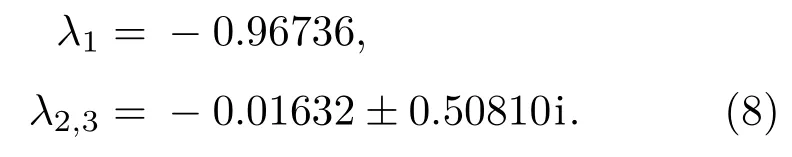
观察(8)式中三个特征值的实部可见,λ1为负实数,λ2和λ3的实部均为负数,因此可以确定平衡点O为一个稳定的平衡点.且经后面的混沌特性分析可知,系统((5)式)是一个混沌系统,其吸引子类型为隐藏吸引子.由Shilnikov定理[9]可知,系统产生混沌的条件要求至少存在一个不稳定的平衡点,同时吸引子也来源于这个不稳定的平衡点,而这类具有隐藏吸引子的混沌系统的出现,对传统的混沌判定准则提出了新的挑战.

2.3 混沌特性分析

分岔图是非线性动力学研究中的一个重要工具,可以显示系统随某个参数的动力学变化.以系统((5)式)的阶次q为变化量,令初始值为[x(0),y(0),z(0)]=(0.5,0,0.2),得到状态变量x随着阶次变化的分岔图,如图1所示,此分岔图采用最大值法绘制.

观察图1可知,系统((5)式)处于混沌运动状态的阶次范围很小,大部分区域都是稳定状态,并且到了一定数值后,对于阶次变化非常敏感.当q＜0.987时,系统的运行轨迹趋于一稳定值,表明系统的运动特性是稳定的.当0.987≤q＜0.990时,系统发生倍周期分岔.当0.990≤q≤1.000时,系统已完全进入混沌运动状态.

图1 变量x随阶次q变化的分岔图Fig.1.Bifurcation diagram of variable x with order q.

通过相轨迹图、Poincare映射、功率谱进一步分析系统的非线性动力学特征.结合对分岔图的分析,取q=0.990,初始值[x(0),y(0),z(0)]=(0.5,0,0.2),进行数值仿真分析.

首先,取仿真时间Tsim=500 s,步长h=0.005,利用预估校正数值算法,得到系统的相轨迹图和变量x的时域图分别如图2和图3所示.显然,系统((5)式)处于混沌状态,同时表现出单涡卷特性,且具有一个混沌吸引子,由伸展的螺旋运动和折返的单向运动组成,其随机性主要在于折返运动的不确定性.该系统仅有一个稳定平衡点,按照Shilnikov定理[9]要求至少存在一个不稳定的平衡点才会出现混沌的判定标准,该系统不会出现混沌,然而图2和图3表现出显著的混沌行为,也与图1分岔图的表现相对应,因此系统((5)式)是一个分数阶混沌系统.

取z=0的截面,得到系统((5)式)的Poincare截面图,如图4所示,可以看出其Poincare截面由沿着不可数点的两条线构成,对应着吸引子伸展的螺旋运动,具有分形结构的密集分布特点.取采样频率为1.5 Hz,仿真时间Tsim=1000 s,得到系统((5)式)的功率谱如图5所示,可以看出系统的功率谱是连续谱,且无明显的峰值.由此,从Poincare截面和功率谱进一步得出系统处于明显的混沌状态.

图2 系统((5)式)的相轨迹图 (a)在x-y-z空间;(b)在x-y平面上;(c)在x-z平面上;(d)在y-z平面上Fig.2.Phase portraits of system(Eq.(5)):(a)In the x-y-z state space;(b)in the x-y plane;(c)in the x-z plane;(d)in the y-z plane.

图3 x时域图Fig.3.Time series of state variable x.

图4 z=0时x-y平面上的Poincare映射Fig.4.Poincare mapping on x-y phase plane with z=0.

图5 功率谱Fig.5.Frequency spectrum.

3 分数阶系统有限时间同步

3.1 分数阶系统有限时间稳定性理论

分数阶混沌同步在保密通信领域具有更大的潜力,得到了人们的广泛关注,各种分数阶混沌同步方法被提出,如Lyapunov方程法、驱动-响应法、广义同步法、线性分离投影同步法等.其中,赵灵冬等[24]提出了一种分数阶系统有限时间稳定性理论,能够实现同步误差在有限时间内稳定,具有同步速度快、鲁棒性强等优点.本文运用分数阶系统有限时间稳定性理论实现系统同步控制.

定理1[24]考虑一般的分数阶系统,满足

式中v=x(xq)T.

引理1当满足a,b＞0且0＜c＜1时,可得如下不等式:

令系统((5)式)为驱动系统,其中q=0.99,则相应的响应系统为

式中u1,u2,u3为根据定理1所加入的控制器.

设e1=x1−x,e2=y1−y,e3=z1−z为驱动系统((5)式)与响应系统((12)式)的同步误差,则得到误差系统为

由定理1,设计相应的控制器u1,u2,u3:

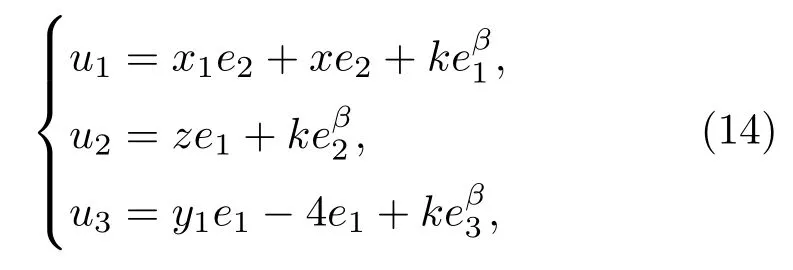
式中k和β为控制器的相关参数.

加入(14)式的控制器后,分数阶误差系统((13)式)可以在有限时间t内达到稳定,

证明由误差系统((13)式)和所设计控制器((14)式),得到同步误差为

根据(9)式推导可得

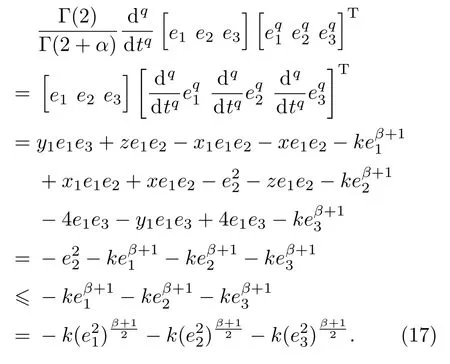
由引理1的不等式得

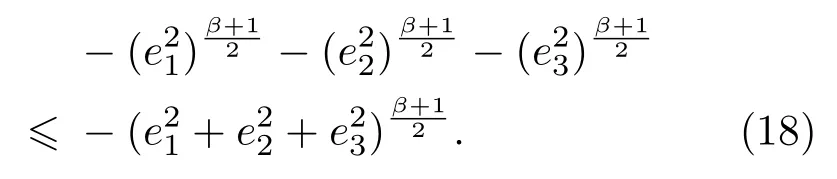
因此可得

显然,(19)式满足定理1的条件,故误差系统((13)式)可以在有限时间t内达到稳定,即驱动-响应系统在有限时间内实现同步,

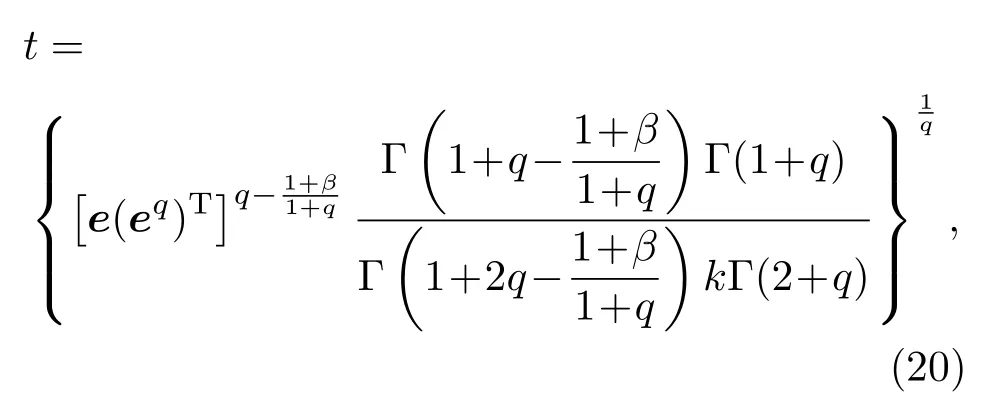
3.2 数值仿真

采用MATLAB R2017a进行数值仿真,用预估校正法求解微分方程.令仿真的步长tΔ=0.001,仿真时间Tsim=12 s,分数阶系统的阶次取q=0.99,驱动系统((5)式)和响应系统((12)式)的初值分别取为[x(0),y(0),z(0)]=(0.5,0,0.2)及[x1(0),y1(0),z1(0)]=(1.2,0.3,2).设计控制器的相关参数取值为k=1.5,β=0.8.根据这些参数编写程序,得到误差系统和各状态变量同步情况的仿真图,如图6和图7所示.

图6 同步误差曲线图Fig.6.Synchronization error curves.

由图6可以看出,加入控制器后误差系统e1,e2和e3在3 s内均能收敛于零点,即误差系统达到稳定状态,由图7也可看出,驱动系统和响应系统的各状态变量在3 s内达到了完全同步状态,由此可见设计的控制器效果非常显著.

图7 加入控制器后各状态变量同步图 (a)变量x-x1;(b)变量y-y1;(c)变量z-z1Fig.7.Synchronization phase plots of state variables with controller added:(a)x-x1;(b)y-y1;(c)z-z1.

4 结 论

基于Sprott E系统,构建了仅有一个稳定平衡点的分数阶混沌系统,研究含有隐藏吸引子的分数阶混沌系统,通过平衡点、吸引子、Poincare映射和分岔等详细分析了该系统的基本动力学行为.基于分数阶有限时间同步控制理论,设计了有限时间同步控制器,实现了带有隐藏吸引子分数阶混沌系统的同步控制,数值仿真结果证实了该方法的有效性.构建的分数阶混沌系统具有以下特点和优势:首先,用分数阶微积分进行描述和研究,其物理意义更清晰,描述更精确,能更好地揭示对象的本质及其行为特性;其次,构建的改进分数阶Sprott E系统在平衡点处有一对具有负实部的共轭特征根,系统具有稳定的平衡点,吸引子类型为隐藏吸引子;最后,构建的分数阶混沌系统具有更复杂、更丰富的混沌动力学特性,参数选择范围更大、更加灵活,且系统对这些参数的变化较为敏感,这样在构造混沌振荡器应用于保密通信、图像加密等实际领域时,密钥更多更复杂,增强了不可预测性,提高了应用中的可靠性和安全性.

[1]Lorenz E N 1963J.Atmos.Sci.20 130

[2]Rössler O E 1976Phys.Lett.A57 397

[3]Chen G R,Ueta T 1999Int.J.Bifurcation Chaos9 1465

[4]Liu C X,Liu T,Liu L,Liu K 2004Chaos Solitions Fractals22 1031

[5]Lü J H,Chen G R 2002Int.J.Bifurcation Chaos12 659

[6]Liu W B,Chen G R 2003Int.J.Bifurcation Chaos13 261

[7]Qi G Y,Chen G R,Du S Z,Chen Z Q,Yuan Z Z 2005Physica A352 295

[8]Bao B C,Liu Z,Xu J P 2009J.Sys.Eng.Electron.20 1179

[9]Shilnikov L P 1965Sov.Math.Dokl.6 163

[10]Leonov G A,Kuznetsov N V,Vagaitsev V I 2011Phys.Lett.A375 2230

[11]Molaie M,Jafari S,Sprott J C,Golpayegani S M R H 2013Int.J.Bifurcation Chaos23 1350188

[12]Wang X,Chen G R 2012Commu.Nonlinear Sci.Numer.Simul.17 1264

[13]Jafari S,Sprott J C,Golpayegani S M R H 2013Phys.Lett.A377 699

[14]Wei Z 2011Phys.Lett.A376 102

[15]Jafari S,Sprott J C 2013Chaos Solitions Fractals57 79

[16]Li Q D,Zeng H Z,Yang X S 2014Nonlinear Dyn.77 255

[17]Leonov G A,Kuznetsov N V,Mokaev T N 2015Commu.Nonlinear Sci.Numer.Simul.28 166

[18]Zhang Y A,Yu M Z,Wu H L 2016Acta Electron.Sin.44 607(in Chinese)[张友安,余名哲,吴华丽2016电子学报44 607]

[19]Pecora L M,Carroll T L 1990Phys.Rev.Lett.64 821

[20]Li C G,Liao X F,Yu J B 2003Phys.Rev.E68 067203

[21]Jia H Y,Chen Z Q,Yuan Z Z 2010Chin.Phys.B19 020507

[22]Zhang L,Yan Y 2014Nonlinear Dyn.76 1761

[23]Wang D F,Zhang J Y,Wang X Y 2013Chin.Phys.B22 100504

[24]Zhao L D,Hu J B,Bao Z H,Zhang G A,Xu C,Zhang S B 2011Acta Phys.Sin.60 100507(in Chinese)[赵灵冬,胡建兵,包志华,章国安,徐晨,张士兵 2011物理学报60 100507]

[25]Podlubny I 1999Fractional Differential Equations(San Diego:Academic Press)p18

[26]Sprott J C 1994Phys.Rev.E50 647