高雷诺数双螺旋涡尾迹演化特性分析∗

李高华 王福新

(上海交通大学航空航天学院,上海 200240)

(2017年6月5日收到;2017年9月18日收到修改稿)

1 引 言

螺旋状涡尾迹是流体在旋转受力面的作用下产生的一种特殊的漩涡流动现象,如直升机旋翼尾迹、风力机尾迹以及螺旋桨尾迹等,是由受力面梢部脱出的集中涡和后缘脱出的尾迹面组成的流动演化系统.由于受力体工作在尾迹附近,因此涡尾迹的演化特性很大程度地决定了旋转面的气动性能.

与固定受力面,如固定翼飞机等,的涡尾迹[1,2]不同,螺旋状涡尾迹由于旋转而受到额外的非惯性力作用,如科氏力和离心力等,涡系演化中非线性现象更加丰富,流动特征也更加复杂.集中卷起的桨尖涡在尾迹流动中占据主导作用,是螺旋涡尾迹流场的“骨架”,因而受到了广泛的关注.为研究悬停旋翼尾迹的动态特性,Mula等[3,4]对桨尖涡演化过程进行了立体粒子图像测速法(PIV)测量,发现随着涡龄的增大,涡系具有明显的抖动和漫游现象,并且这些非稳态现象呈现明显的空间各向异性和时间周期性.Komerath等[5]在研究中发现,实验测量与经典升力线理论预测的桨尖涡强度相差甚远,前者仅占后者的40%,这一巨大差异归因于尾涡面的反向卷起,进而削弱了桨尖涡的强度.McAlister[6]研究发现,桨尖涡在第一个转动周期内的平均强度仅占桨叶附着涡强度的53%,这同样说明在此过程中伴随着大量的附着涡从后缘脱落,并随后在桨尖涡管附近卷起成集中涡.Milluzzo和Leishman[7]采用高分辨率PIV技术对旋翼尾迹涡面在不同载荷下的演化行为进行了测量,结果表明,从后缘脱落的小尺度反向尾迹涡对快速向湍流区集中,并进而成为下游尾迹区湍流的主要来源,另一方面,桨叶载荷对尾涡面与桨尖涡之间的相互作用具有重要影响.Jain和Conlisk[8]在对桨尖涡远场相互作用的研究中发现,相邻涡管间存在周期性的穿越现象,并把这种现象与涡环相互作用中的“蛙跳”穿越进行了对比,发现两者存在明显的相似性.

机理研究方面,在中小雷诺数甚至忽略黏性效应的前提下,在以下几个方面取得了进展:1)桨尖涡时空不稳定性,如Widnall[9]、Hattori和Fukumoto[10,11]、Sarmast等[12]、Sørensen[13]以及Lignarolo等[14]的工作,通过理论分析证实桨尖涡演化过程中存在短波不稳定、长波不稳定、进动不稳定和曲率不稳定等现象;2)桨尖涡参数的自相似行为,如Ali和Abid[15]对单桨叶旋翼桨尖涡的研究结果表明,当雷诺数Re≤2000时,桨尖涡涡核特征变量,如涡量分布、周向速度分布等,随涡龄的变化表现出自相似特性;3)桨尖涡局部流场的模态特征,基于本征正交分解,从主控模态的角度对桨尖涡流动特征进行分析和解释,如Sarmast等[12]、Mula和Timey[16]以及Hamilton等[17]的工作.

尽管目前在桨尖涡系流动现象和机理方面均取得了一定的研究成果,受实验测量手段以及理论模型复杂程度的限制,对于在实际问题中常见的高雷诺数(百万量级)、多桨条件下螺旋涡系的演化问题,仍需要进一步的研究.本文利用数值方法对双桨叶刚性Caradonna-Tung(C-T)旋翼在Re=1.92×106下的双螺旋涡尾迹的演化进行了研究,为了减少对流场的模化以及数值黏性带来的影响,通过使用延迟脱体涡模拟(delayed detached eddy simulation,DDES)方法和高阶迎风/中心低耗散格式,获得螺旋状涡尾迹的三维高分辨率非定常流场.通过桨叶表面压力系数和桨尖涡轨迹与实验值的对比以及尾迹区湍动能的分解比例验证了计算结果的可信性.在此基础上,测量了瞬态流场中桨尖涡关键参数的空间分布规律,通过对桨尖涡局部流场的本征正交分解(proper orthogonal decomposition,POD),给出了不同模态的流动特征以及在桨尖涡状态演化中的作用;使用拉格朗日拟序结构(Lagrangian coherent structures,LCS)研究了轴截面上漩涡系的演化特征,对涡配对、共旋穿越等现象的流动机理进行了分析.

2 数值分析方法

2.1 高分辨率流场计算方法

本文求解的积分形式流体动力学控制方程为

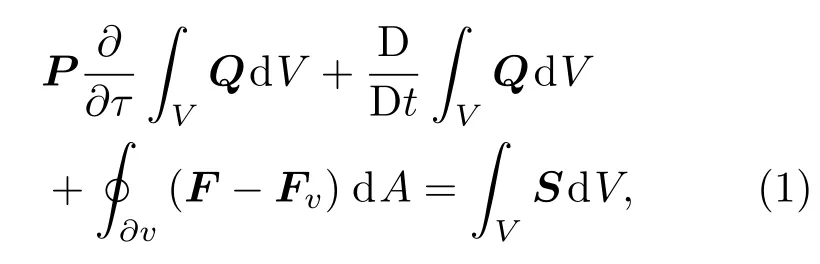
方程基于随桨叶旋转的非惯性坐标系,其中P为Weiss-Smith预处理矩阵[18],用以改善方程在低马赫数时的刚性;Q为守恒变量;F和Fv分别表示对流矢通量和黏性矢通量;右端源项S包含了由坐标系旋转而引起的科氏力和离心力贡献.

使用基于Spalart-Allmaras的DDES方法[19]来模化湍流的影响,这种雷诺平均/大涡模拟(RANS/LES)混合模型,在桨叶物面边界层中使用RANS模型,而在远离壁面的尾迹涡区域自动切换成大涡模拟.

采用重叠网格方法对计算域进行空间离散,桨叶附近(近场)使用结构化贴体网格在物面附近生成适合模拟边界层流动的大长宽比计算单元,背景网格(远场)使用基于八叉树的块结构化笛卡尔网格,根据流场中涡量的大小和梯度对桨尖涡流区域的背景网格进行自适应加密,以提高桨尖涡的空间分辨能力.网格重叠区使用三线性插值进行数据传递以实现全流场耦合计算.

为降低数值黏性对流场漩涡特征的污染,网格单元界面上的对流通量使用5阶WENO和6阶中心混合格式[20]进行计算,混合系数基于流场特征在0到1之间进行自适应调节,在LES涡流区域该系数趋于0,使用低耗散中心格式以提高小尺度涡的分辨能力,其他区域内该系数变为1,使用迎风格式以保持计算稳定性.

桨叶表面使用无滑移边界条件;远场使用基于预处理欧拉方程推导的特征边界条件,以减小远场反射对收敛性带来的不利影响.

程序使用消息传递接口(message passing interface,MPI)根据近/远场求解器、重叠网格信息交换模块对全局通信域进行分组,使得各模块在各自相对独立的子通信域中根据自身并行策略运行,从而实现程序整体上进行大规模并行计算.

2.2 快照POD方法

POD方法使用有限数据集合来提取数据中的主要模态特征,是研究流体流动机理的强有力工具.原始的POD方法涉及高阶自相关矩阵的特征值求解问题,内存要求高,计算开销大,且容易出现数值不稳定.快照POD方法[21]克服了这些缺陷,提高了求解稳定性和计算效率,在流场结构特征诊断和识别等方面得到了广泛应用[22−24].鉴于快照POD算法已经较为成熟,本文不再对其基本原理进行赘述.

本文使用快照POD方法来研究瞬态桨尖涡流场空间分布的主导模态.因此,与通常在同一空间内沿时间序列提取快照数据不同,本文所有快照数据取自同一时刻但不同涡龄的局部流场,快照区域使用极坐标描述,极点位于桨尖涡涡心,区域的半径按照桨尖涡最大半径合理选取.这样,快照POD求解的是同一时刻、不同涡龄的局部漩涡速度流自相关矩阵的特征值问题,POD结果所得的主导模态反映的是某一时刻、沿涡龄变化的桨尖涡局部流场的流动特征;POD权重系数随涡龄的变化反映了这些流动特征的空间演化.

2.3 切片LCS方法

欧拉方法描述的漩涡流动特征诊断方法,如涡量、Q准则、λ准则等,通常仅使用某瞬时流场中速度梯度张量及其变形量来表达,虽然能够在一定程度上刻画出瞬态漩涡流场的流态,但均不包含任何与时间相关的信息,无法准确地反映出与时间相关的漩涡流动结构的历史累积效应及其演化过程;再者,使用这些准则来识别漩涡流场中的拟序结构,均需要人为给定截断阈值,不同的阈值下得到的漩涡形态可能差别很大,因而缺乏客观性.拉格朗日描述方法在整个流体输运过程中对所有流体粒子的运动进行跟踪,不仅仅依赖于瞬态流场,而且还依赖于整个流动演化过程,能够反映出漩涡流场结构的时间累积演化效应,在研究时间相关的复杂漩涡流场结构特征演化方面具有独特的优势[25,26].

LCS就是一种使用拉格朗日描述方法来区分时变流场中不同动力学特征区域的拟序结构.有许多种方法可以用来提取出时变流场中的LCS,其中,Haller[27,28]提出的基于有限时间李雅普诺夫指数(finite-time Lyapunov exponent,FTLE)场来提取LCS的方法是最常用和最有效的手段之一.这种方法使用FTLE场中的脊线来提取LCS,无需人为设定阈值,且具有参考系无关性,是一种比较客观的描述方法,在对漩涡主导流动的研究中,如涡环演化、海洋污染物输运和扩散等得到了广泛的使用.

文献[27—29]中给出了FTLE场的具体计算方法,本文直接使用这些算法来完成FTLE场的计算.影响FTLE场空间分辨率的关键参数有:1)初始粒子密度;2)积分时间步长;3)积分时间.为了获取高分辨率的LCS,初始粒子密度需要远大于流场计算使用的网格密度,积分时间应至少包含一个完整的特征输运时间,积分步长取决于样本流场的采集步长以及积分方法。高雷诺数下,螺旋涡尾迹中集中涡的空间尺度相对于整个计算域来说非常小.为分辨这些漩涡,计算网格的最小尺度约占计算域最大尺度的0.02%,因此,使用更大的粒子密度来计算高分辨率三维FTLE场,在内存和计算时间开销上都无法承受.不过,螺旋状涡尾迹具有一定的轴对称特性,并且惯性坐标系中固定轴截面上的时变流场能够反映出桨尖涡的生成、发展以及相互作用,因此可以使用轴截面流场数据来计算FTLE场,进而提取相关LCS,分析漩涡系统的输运和混合特性.

2.4 网格可解及模化湍动能

涡尾迹大涡模拟区域中,流场中的湍动能被分为两部分,网格能够直接分辨出的可解湍动能部分kresolved和网格无法直接分辨出而使用亚格子模型模化的部分kmodeled.这两部分湍动能均使用来流声速的平方进行无量纲化.其中,网格可解部分kresolved无量纲化之后与其定义式在形式上保持相同,即

其中cb1,cw1和fw为模型常数;Δ为亚格子滤波尺度;S为应变率张量.由于模型中不显含模化湍动能,根据亚格子黏性系数场无法直接导出其模化的湍动能分布,本文采用了动态亚格子湍动能模型中亚格子湍动能ksgs和亚格子黏性系数νt之间的关系式

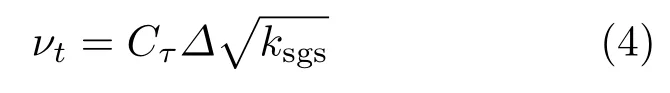
来估算LES区域被模化的湍动能,Cτ为常数.即

其中滤波尺度Δ=max(δx,δy,δz),取网格单元在三个方向上尺寸的最大值.

3 数值计算及结果验证

3.1 计算模型及设置

选用C-T旋翼模型[30]来计算得到双螺旋涡尾迹流场.该模型由两片矩形平直刚性桨叶组成,展向无扭转,展弦比为6,剖面翼型为NACA0012.为方便计算,除去了旋转中心处的桨毂及驱动装置,并切除了桨根10%R以内的部分,R为旋翼半径.模型俯视图及关键尺寸如图1所示.

图1 模型俯视图及关键尺寸Fig.1. Top view and key parameters of C-T rotor model.

该模型有多组试验状态参数,为了在后续分析中剔除可压缩性带来影响,本文选取其中一组亚声速参数进行计算,计算状态主要参数见表1.其中下标tip表示对应于桨尖处的参数,Ma和Re分别表示马赫数和雷诺数,θ表示桨叶的总距角,µ表示前进比,ω为桨尖马赫数对应的桨叶旋转角速度,除了θ外,其余各参数均为无量纲变量.

采用“O”型拓扑对桨叶附近近场区域进行网格划分,“O”网格径向长度约为30%c,其中c为桨叶弦长;每片桨叶周围计算域划分为46个结构化网格块,径向、展向和周向分别布置89,335和518个网格点,并在距离桨尖70%c范围内加密网格;物面边界层第一层网格高度满足y+约为1,最外层边界处的网格单元接近于各向同性,尺寸约为1.5%c.桨叶附近近场网格详细尺寸如图2所示.

表1 计算状态参数Table 1.Computational condition parameters.

为减小远场边界截断的影响,背景网格沿桨盘旋转轴方向向上下各延伸30R,径向15R;为捕捉旋翼涡尾迹,在桨盘平面下方2R范围内进行了自适应加密,使得该区域内的网格为各向同性的正六面体单元,且三个方向上的尺寸均为约5%c.该背景网格与桨叶近场贴体网格组成重叠网格系统,其中一个切面上的网格尺寸及重叠关系如图3所示.在此网格系统的基础上,针对涡量集中卷起的桨尖涡部分进行网格自适应加密,以提高桨尖涡尾迹的空间分辨率.

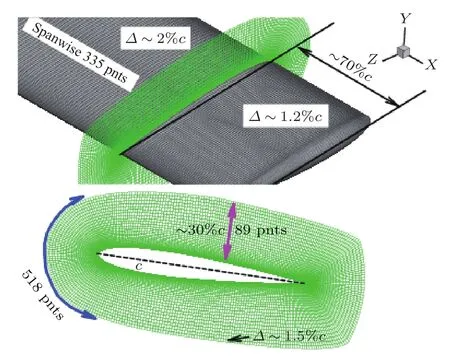
图2 模型附近计算网格及关键尺寸Fig.2. Near-body grid and key parameters of C-T rotor model.

图3 桨叶重叠网格系统切面Fig.3.Slice of rotor blade overset grid system.

使用零速度场初始化全场,为了把流场的启动效应(启动涡)排除到计算域外,首先使用“准非定常”方法建立起基本流场,每个时间步桨叶转动2.5°,包含15个内迭代,共计算了10080个时间步(70转).随后将时间步长减为原来的1/10,即每个时间步桨叶转动0.25°,同时内迭代增加至35次,以保证非定常数值解具有二阶时间精度.“准非定常”计算使用基本网格,随后的非定常计算中,每20个时间步执行一次网格自适应,以捕捉桨尖涡结构.

3.2 平均量验证

图4为桨叶压力系数分布的计算平均和实验测量结果对比,其中参数r/R代表了不同展向位置.从图中可见,计算和实验所得的压力系数分布总体符合较好,偏差主要集中在桨尖附近(r/R=0.96,x/c≈0.025),计算所得的前缘吸力峰值比实验值稍高,这可能与桨尖附近的转捩以及三维流动效应有关.本文使用全湍流模型,没有对边界层转捩进行模化,另外,计算时对桨尖几何外形做了圆角化处理,这也是压力系数出现偏差的原因之一.

计算和实验所得到的桨尖涡涡核垂向及径向位置随涡龄的变化如图5所示.由图可见,随着涡龄的增加,垂向位置差别减小,二者总体上符合较好;而对于径向位置,二者差别则随涡龄的增加而逐渐增大,计算所得的桨尖涡收缩速度比测量结果快,计算和实验所使用的几何模型在桨叶中心附近的不同可能是引起这种差别的主要原因.另外,数值耗散造成的桨尖涡涡量过度耗散也在一定程度上会诱发这种结果.

3.3 尾迹湍动能统计量

本算例在风洞试验中并未对尾迹进行定量或定性的测量,因此,无法直接与实验结果对比来验证尾迹区流场计算结果的正确性.本文通过尾迹区湍动能的网格可解率来间接证明远场LES区域流场计算结果的可信性,所谓湍动能的网格可解率是指LES网格可解湍动能(kresolved)在总湍动能

(kresolved+kmodeled)中所占的比例.

图4 桨叶表面压力系数分布对比 (a)r/R=0.50;(b)r/R=0.68;(c)r/R=0.80;(d)r/R=0.96Fig.4. Comparison of pressure coefficient distribution on rotor blade:(a)r/R=0.50;(b)r/R=0.68;(c)r/R=0.80;(d)r/R=0.96.

图5 桨尖涡轨迹对比Fig.5.Comparison of tip-blade vortex trajectories.

在固连于桨叶上的旋转坐标系中,理想的螺旋涡系在轴截面上形成稳定的二维点涡结构,流场无脉动.实际螺旋涡系流场由于存在内在不稳定性[9],随着涡龄的增加,空间波动现象逐渐显现出来,从而引起轴截面上点涡位置的抖动,进而引发速度场的脉动,最终导致螺旋状涡结构的破碎、湍流化.图6给出的轴截面上湍动能分布很好地显示了这一过程:在桨尖涡脱落后的前两个周期(涡龄＜720°)内,总湍动能数值极小,显示了桨尖涡系空间结构的稳定性;随后,湍动能逐渐增大,并且其分布范围呈现一定的集中性,体现了桨尖涡系空间不稳定性的有界发展;最终,涡系结构的湍流化破碎导致湍动能分布失去了集中性.图6左给出的是LES直接分解出的湍动能占总湍动能的比重,可以看出,在湍动能分布较为丰富的区域内,这一比例超过95%,间接验证了本文远场LES结果的可信性.亚格子模化湍动能主要集中在稳定涡系区域,该区域涡核附近存在湍流区,但尺度太小且在该区域不足以影响桨尖涡的稳定性,因而没有采用更密的网格来计算这些湍流区的行为.

惯性坐标系中,固定轴截面上的二维时变涡结构描述了桨尖涡随涡龄(时间)的变化过程.图7给出了某轴截面上的时均湍动能分布,其中左图为亚格子模化部分,右图为LES分解出的部分.对比图中湍动能的数量级可知,LES成功地分解出了绝大部分湍动能.与图6类似,由右图中湍动能的分布可以定性地得知桨尖涡的大致演化过程.在桨盘平面下方附近,湍动能呈规则的带状分布,说明在该区域内的桨尖涡以稳定的轨迹输运.随着涡龄的增加,湍动能径向分布范围逐渐扩大,数值趋于减小,这一方面由扩散和耗散作用引起,另一方面也暗示了桨尖涡的不稳定性在逐渐增强.在更大涡龄区,湍动能在径向外侧有明显的“外扩”状分布,说明该区域存在明显的涡-涡相互作用,并且这种相互作用具有一定的确定性和周期性,如此才能够在时均轨迹中留下这样形状的痕迹.远尾迹中,由于桨尖涡破碎并湍流化,湍动能显示出“弥散”状分布.

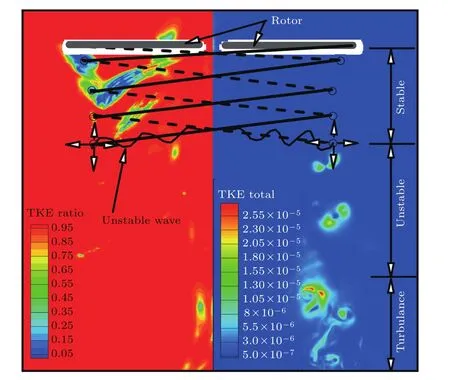
图6 非惯性坐标系下轴截面上的湍动能分布 左图为LES分解出的湍动能占总湍动能的比例;右图为总湍动能分布Fig.6.Turbulent kinetic energy(TKE)on axial slice in non-inertial coordinate system:Left,ratio of resolved to total TKE;right,distribution of total TKE.

图7 惯性坐标系下轴截面上的湍动能分布 左图为亚格子模化湍动能;右图为LES分解出的湍动能Fig.7.Turbulent kinetic energy on axial slice in inertial coordinate system:Left:modeled sub-grid TKE;right:LES resolved TKE.

4 结果与分析

4.1 瞬态流场螺旋涡结构特征

采用Q准则定义的尾迹涡结构,可以反映出某瞬时双螺旋涡尾迹的空间分布形态,如图8所示,其中颜色表示当地速度的大小.由图可见,在脱离桨尖后大约两个周期(720°)内,桨尖涡管结构呈现规则的收缩状双螺旋结构,涡管空间分布光滑稳定.随后,双螺旋中的一支螺距增加并沿径向收缩,与另一支涡管出现配对和穿越现象,同时涡管沿周向出现长波波动,涡系拓扑逐渐失去稳定,直至出现涡管的缠绕以及由此而导致的破碎和湍流化.

桨盘平面下方附近的稳定区域内,螺旋涡管涡心的径向和垂向轨迹如图5所示.垂向位置与涡龄之间的变化呈现分段线性关系,在涡龄为180°处存在斜率不连续,即涡龄小于180°时,斜率约为−0.048R/100°,而涡龄大于180°时,这一斜率变为−0.116R/100°.这种斜率不连续现象主要与后缘尾迹涡面对桨尖涡的诱导作用有关,如图9所示.后缘尾迹涡面由于处于桨尖涡下洗速度场中而具有更快的下降速度.涡龄＞180°时,新生成的后缘尾迹涡面快速向下运动,与桨尖涡快速接近产生相互作用,加快桨尖涡的垂向输运过程,同时在桨尖涡的诱导下,后缘尾迹涡面反向卷起成集中涡.后缘尾迹涡没有对桨尖涡的径向分布产生明显的影响,在180°附近没有发现任何不连续现象.

图10给出了桨尖涡涡心涡量随涡龄的衰减特性,涡量的方向沿涡管轴向,即螺旋线的切向.图中给出了4个时刻的结果,每个时刻相隔1/4旋转周期.从图11可以看出,不同时刻的衰减特性几乎完全重合,说明旋转坐标系中的结果在一定涡龄范围内(本算例为＜720°)具有定常特性,这也是工程上在旋转坐标系中采用定常算法快速评估旋翼悬停气动性能的主要依据.对数据的拟合结果表明,在这一涡龄范围内,涡量的衰减特性符合幂函数规律,系数如图10所示.根据这一规律给出的衰减速率曲线表明,涡量在刚脱离桨尖时衰减最快,随后衰减速率快速减小并最终趋于0.

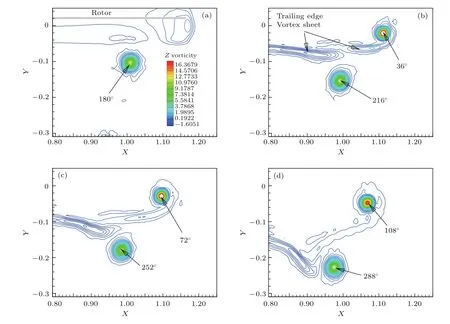
图9 后缘尾迹涡面对涡龄大于180°的桨尖涡的诱导作用Fig.9.Interaction of trailing edge vortex sheet to blade tip vortex after 180°vortex age.

图10 桨尖涡轴向涡量随涡龄的衰减特性Fig.10.Decay characteristic of axial-vorticity as vortex age for tip vortex.

涡管中心轴向涡量随涡核径向和垂向轨迹的变化趋势如图11和图12所示.涡龄小于720°时,变化趋势总体上符合幂函数曲线.图11表明涡龄较小时,随着涡管收缩,轴向涡量快速衰减.涡龄大于720°时,随着涡量的进一步衰减,涡管无法继续保持稳定收缩,径向轨迹出现不稳定,径向位置随涡龄的增加快速外扩,表明稳定的螺旋结构被打破.在涡龄为180°时,涡管轴向涡量随垂向位置的变化趋势(图12)出现斜率不连续,但分段的两部分均满足幂函数分布.

图11 螺旋涡管中心处最大轴向涡量随径向轨迹变化趋势Fig.11.Variation trend of maximum axial vorticity with radial trajectory at helical vortex tube center.

图12 螺旋涡管中心处最大轴向涡量随垂向轨迹变化趋势Fig.12.Variation trend of maximum axial vorticity with vertical trajectory at helical vortex tube center.

图10—图12中幂函数参数的物理意义与流动状态相关,但由于受计算资源的限制,本文没有就这些参数随流动状态的变化开展参数化分析.

为研究螺旋涡管半径及涡管速度环量的空间变化特性,提取了不同涡龄的涡管局部速度场切片.图13所示的圆域代表了不同涡龄切片的局部流域,圆域中心位于局部流线所确定的漩涡中心,速度场投影到圆域所确定的局部极坐标系中,图13中显示的是极角方向速度等值线,用于确定涡边界并积分获得环量.

图14为涡龄为18°的桨尖涡周围周向速度分布,以及采用Q准则(Q=0.05)和Scully涡模型确定的涡边界,其中Q准则确定的涡边界由图8中的涡管结构经相应轴截面截取得到.Scully涡模型是广泛用于旋翼自由尾迹分析的一种理论涡模型,它所定义的漩涡周向速度具有如下的分布:

其中Γ表示漩涡速度环量,用于描述漩涡的强度;rc为涡半径;r为径向位置坐标.Scully模型涡边界使用周向速度最大值确定.从图14中可以看出,两种方法确定的涡核中心位置大致相同,但都与极坐标原点位置有所偏差,这是由于周向速度分布不均造成的.Scully模型所确定的涡核半径稍大于Q准则的涡核半径,这与Q准则考虑了第三维速度场有一定关系.

图15是根据Scully模型所确定的漩涡平均半径rc、速度环量Γ以及据此计算得到的周向速度分布,作为对比,同时给出了CFD计算得到的平均周向速度分布.由图中可见二者符合得很好,这也说明了旋翼尾迹计算中采用Scully模型的合理性.随着涡龄的增加,涡核半径的变化趋势如图16所示,其中的散点是本文计算结果采用Scully模型得到的涡核半径,曲线是利用Squire涡核半径增长模型得到的结果.Squire模型描述了涡核半径随涡龄的变化趋势:

图13 螺旋涡管中心处最大轴向涡量随垂向轨迹变化趋势Fig.13.Variation trend of maximum axial vorticity with vertical trajectory at helical vortex tube center.

图14 涡龄为18°的桨尖涡周向速度分布以及使用Q准则和Scully涡模型确定的涡边界Fig.14.Circumferential velocity distribution and vortex boundaries determined by Q criterion and Scully vortex model for tip vortex at age of 18°.

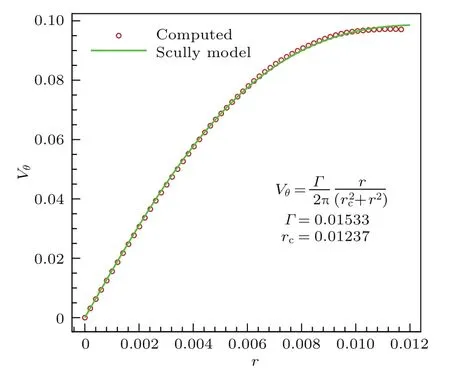
图15 计算以及Scully涡模型的周向速度分布Fig.15.Computed and Scully modeled circumferential velocity distribution.

图16 计算以及Squire模型的涡核半径随涡龄变化规律Fig.16.Computed and Squire model determined vortex core radius variation.

其中r为涡核半径,r0为桨尖涡起始涡核半径;α=1.2564为Oseen常数;ν和νt分别表示运动分子黏性和涡黏性系数;Retip和Matip表示基于桨尖速度的雷诺数和马赫数;ω表示转速;ϕ表示涡龄.涡龄较小时,计算结果与模型相符得较好;大涡龄情况下,计算得到的涡核半径在模型附近振荡,出现了较大的偏差,这体现出大涡龄状态下,螺旋涡内不稳定性的发展使得涡核半径的演化表现出了更大的非线性.

图17显示的是桨尖涡速度环量随涡龄的变化趋势,环量由公式

计算得到,积分路径沿涡边界极角增大的方向.从图中可以看出,桨尖涡从桨叶脱落之后,涡龄小于约100°范围内环量稳定增长,说明在这段时间内来自桨叶转动的能量仍然可以有效地注入到桨尖涡中,桨尖涡从桨叶中汲取能量使之持续生长,强度不断增强.随后,环量基本保持不变,这说明桨尖涡生长和耗散达到了基本平衡,从约400°开始,耗散机制开始占据主导,环量出现减小的趋势.

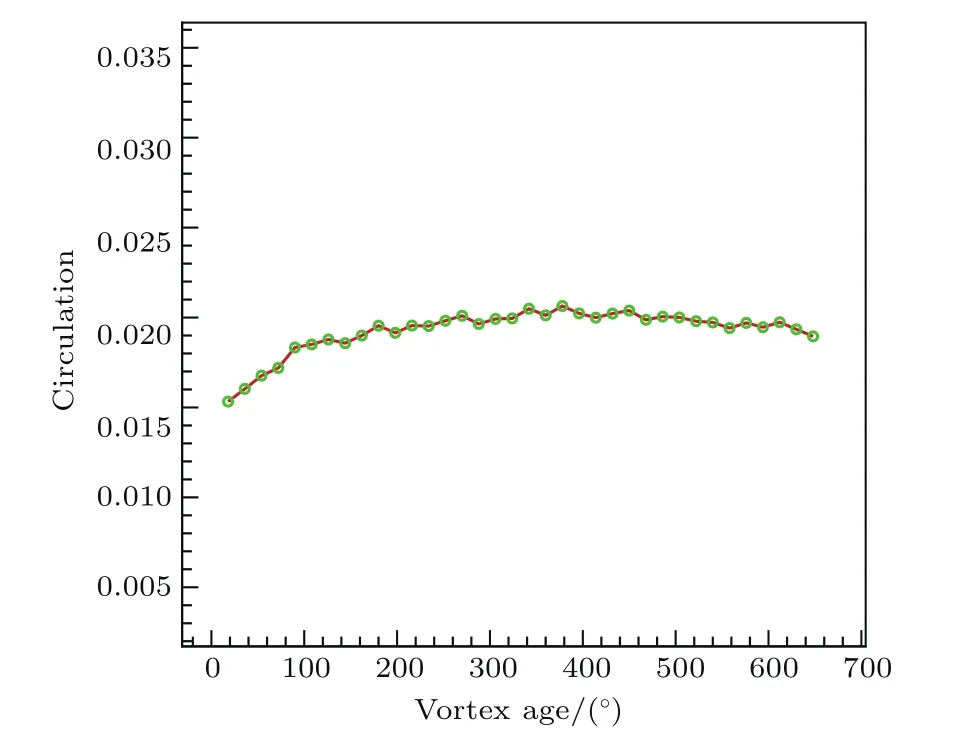
图17 环量随涡龄的变化趋势Fig.17.Variation trend of circulation with vortex age.

为进一步分析桨尖涡的流动形态,使用POD方法对不同涡龄的桨尖涡速度场切片进行了本征正交分解.图18给出了前i个模态的能量占总能量的比重,这里的能量使用POD中的特征值来衡量.由图可知,第1个模态的能量占总能量的96.15%,而前三个模态的能量总和占总能量的99.8%,因此只需要分析前几个主要模态的流动特征即可以对桨尖涡的演化特性进行深入的了解.

图19给出的是前6个模态的流场及流线分布,图中等值线为POD分解之后x方向的速度分布.从图中可见,从第1至第6模态,流场特征及流线拓扑趋于复杂化,位于区域中心的漩涡强度逐渐变弱.前两个模态具有明显的特征,第1个模态为纯点涡,第2个模态为来流与点涡的叠加,其他模态为多个点涡共生的复杂模态.

经过POD分解之后,任意涡龄的漩涡流场都可以使用基本模态的线性叠加来表示.通常情况下前几阶模态占据了绝大部分能量,因此可以前几阶模态线性叠加所得的近似流场包含原流场中的绝大部分流动特征.图20显示了前6个模态在不同涡龄时的权重分布,由图可见,权重较大的为前四阶模态,其余模态的权重分布比较稳定,落在(−0.5,0.5)区间内.在所考虑的涡龄范围内,第1模态的权重远大于其他模态,这体现了点涡流动的主导作用.图中显示,点涡模态的权重随着涡龄的增加而减小,这是涡量随涡龄衰减结果的体现,尤其显著的是,第2模态的权重在涡龄为180°附近出现了间断性跳跃,并且符号发生了改变,这进一步解释了桨尖涡垂向轨迹在涡龄为180°附近出现的拐折现象,在涡龄大于180°时,第2模态权重为负值,表明图19(b)中的流动方向反向向下,这加快了桨尖涡的垂向输运速率,并且随后第2模态的权重几乎保持不变.在大涡龄条件下,流态更为复杂的第3模态权重增加,表明桨尖涡将逐渐表现出不稳定现象.

图18 前i个模态的能量占模态总能量的比重Fig.18.Energy ratio of previous i modal to total.

图19 前6个模态的流线Fig.19.Streamline of the first 6 modal.

图20 前6个模态在不同涡龄时的权重Fig.20.Weights of the first 6 modal at different vortex ages.

4.2 拉格朗日体系下桨尖涡系的演化

为研究桨尖涡系的时间演化特性,利用有限时间李雅普诺夫指数场,计算得到了与参考系无关的拉格朗日拟序结构,使用该结构对桨尖涡时变系统的演化特性进行分析.图21为惯性坐标系下某轴截面上不同时刻对应的FTLE场,FTLE积分时长为一个转动周期,不同的积分时长会影响FTLE数值的大小,但不会改变FTLE的分布.图中顶部为桨盘平面所在位置,底部延伸至2.2R处,左侧位置为44%R,右侧为105%R.

从图中可以清晰地分辨出由FTLE脊线组成的LCS,根据这些LCS的演化特征可以相应地阐述涡系的演化过程.随着时间的推移,图21(a)中的涡结构V1,V2,V3等向下方输运,新的桨尖涡V0生成并逐渐发展长大;V2和V3相互靠近并出现涡配对现象;下方更大涡龄的涡对出现相互绕转,三维情况下对应于涡对的穿越与缠绕;远场中的LCS变得更加复杂和不规则,对应于涡的失稳破碎及湍流混合过程.

比较图21(a)和图21(d),顶部前两个漩涡形态结构几乎完全相同,可知两片桨叶通过该截面后形成的涡旋表现形式相同,即在该截面上,顶部前两个漩涡的演化主要受桨叶旋转的影响,具有T/2周期性,其中T为桨叶旋转周期.第三个漩涡虽然形态相似,但其周围LCS完全不同,剩余漩涡更不具有T/2周期性,这说明随着涡龄的增长,涡的演化受桨叶旋转的影响变小,而受远场更大涡龄的漩涡演化的影响加剧.涡配对之后出现的共旋削弱了向下输运的部分动能,且共旋具有自身周期(略大于T),这是导致远场流场逐渐丧失周期性的主要原因.

图21 半个旋转周期内惯性坐标系某轴截面上有限时间李雅普诺夫指数场的演化 (a)t时刻;(b)t+T/6时刻;(c)t+2T/6时刻;(d)t+3T/6时刻Fig.21.Evolution of finite time Lyapunov exponent field in an axial slice of inertial coordinate system in half rotation period:(a)At time t;(b)at time t+T/6;(c)at time t+2T/6;(d)at time t+3T/6.

由于桨尖涡在小涡龄时具有周期性,图22给出了一个周期(T/2)内桨尖涡的演化过程,除FTLE场外,同时还给出了粒子群的分布以便于更直观地描述漩涡对周围流体的卷吸过程.漩涡从生成到长大的演化顺序为:第一阶段V0,(b)(c)(d)(e)(f)(a);第二阶段V1,(a)(b)(c)(d)(e)(f).第一阶段演化过程中漩涡不断长大,且没有新的漩涡生成,这一过程中漩涡的特点是形态相似,尺寸渐增;第二阶段过程中,漩涡受上游新生成的涡的影响而出现变形,并伴随着二次涡的生成.

第一阶段中,桨尖涡不断卷吸夹带周围流体粒子而逐渐稳定地长大,该过程所受下游漩涡的影响较小,流动过程简单明了.第二阶段开始时,漩涡周围存在三条比较明显的LCS,如图22(a)所示,把漩涡周围的流体域分成了动力学相异的三个部分,LCS1和LCS3形成的流域位于桨盘半径R以内,流体粒子通过桨盘下洗进入该区域;LCS1和LCS2形成的流域位于桨盘半径以外;而LCS2和LCS3之间的流域属于下游漩涡的一部分.这三个流域内的流体粒子无法穿过LCS线进行混合,而只能分别被卷吸到漩涡内部夹层之中;随着新的桨尖涡的生成及其卷吸作用,并伴随着后缘涡面(trailing edge vortex sheet,TEVS)的挤压,LCS1出现了变形,LCS1和LCS2之间的流道变窄,如图22(b)—(d)所示,并最终导致流道封闭,失去进一步夹带流体粒子的能力,如图22(e)和(f)所示,同时在TEVS的作用下,LCS1反向卷起衍生出后缘尾迹涡面二次涡.

图22 小涡龄下桨尖涡在一个周期内的演化过程 (a)t时刻;(b)t+T/6时刻;(c)t+2T/6时刻;(d)t+3T/6时刻;(e)t+4T/6时刻;(f)t+5T/6时刻Fig.22.Evolution of young age tip vortex in one period:(a)At time t;(b)at time t+T/6;(c)at time t+2T/6;(d)at time t+3T/6;(e)at time t+4T/6;(f)at time t+5T/6.

随后,漩涡V1与下游的V2快速接近,如图23(a)所示,反向旋转的二次涡快速下移,并与V2涡接触形成封闭的豆荚状LCS结构,如图23(c)所示,完成漩涡的配对,同时,由于二次涡的夹带作用,V1和V2组成的涡对开始做共旋运动,旋转方向与V1和V2相同.在涡对的共旋过程中伴随着对流体粒子的夹带和卷吸,如图23(f)所示.

随着涡对的旋转,其整体对流体粒子的夹带通道逐渐变窄,直至闭合,如图23(g)和(h)所示,形成更为复杂的共旋结构,包含原来的涡对和上游下洗而来的反向旋转二次涡.由于组成该复杂旋转体的漩涡旋向不同,反向二次涡与豆荚状涡对快速拉伸变形,同时豆荚状涡对在三维情况下出现轴向断裂,导致漩涡结构的破碎,最终出现湍流混合流动,如图21远场流态所示.

在整个演化过程中,后缘尾迹涡面的卷起及其与桨尖涡的相互作用对漩涡形态、涡配对以及涡对的共旋等现象产生重要影响,它通过影响流场内LCS的形态及分布来支配不同区域的流体粒子的动力学特性,从而激发了下游漩涡复杂的动力学行为.

图23 漩涡配对及共旋演化过程(Δt≈3T/16)Fig.23.Evolution of vortex pairing and co-rotating(Δt≈ 3T/16).

5 结 论

基于高分辨率数值模拟方法,对高雷诺数下双桨叶旋翼悬停涡流场进行了非定常数值模拟,计算结果清晰地显示出了双螺旋桨尖漩涡的复杂空间结构,以及从近场稳定状态到远场不稳定状态直至漩涡破碎湍流化的整个空间演化过程,通过对漩涡关键参数的空间分布及拉格朗日描述的流场拟序结构的时间演化分析,得出以下结论.

1)桨尖涡涡核垂向轨迹随涡龄的变化曲线在180°涡龄处出现拐折现象,使得在大于180°涡龄时桨尖涡下降速度明显变大,从每百度下降0.048R增大至每百度0.116R,上游新生成的后缘尾迹涡面卷起的反向旋转二次涡的快速下洗作用是产生这一现象的主要原因.

2)涡龄小于约720°时,在固定于桨叶上的旋转坐标系中观察,双螺旋桨尖涡具有定常特性,不同时刻下涡心涡量随涡龄的衰减规律几乎完全重合,均按照幂函数规律进行衰减,衰减速度随着涡龄的增加而逐渐趋于0.此外,涡核中心涡量随螺旋涡径向及垂向轨迹均按照幂函数规律变化,并且涡量随垂向轨迹变化曲线在180°涡龄处产生分段.

3)稳定的螺旋涡周向速度Vθ与到涡心径向距离r的关系满足Scully涡模型,涡核半径随涡龄的变化规律符合Squire模型,验证了工程上使用涡模型及涡半径演化模型在稳定区内的合理性;漩涡的环量在涡龄小于100°时稳定增长,该阶段为桨尖涡生长阶段,随后环量保持不变,为桨尖涡平衡阶段,在约400°时,环量开始逐渐减小,为桨尖涡耗散衰减阶段.

4)稳定区POD模态中,占据绝对主导的第一模态为点涡模态,其次为第二模态自由来流与点涡的叠加.对各模态权重随涡龄变化趋势的分析发现,在涡龄为180°附近,第二模态的权重发生了明显的跳跃性变化,改变了模态权重的符号,结合结论1),可知后缘尾迹涡面卷起的二次涡导致了第二模态权重的突变.

5)使用拉格朗日拟序结构方法清晰地展示了轴截面上漩涡的生成、稳定生长、涡配对、共旋直至漩涡破碎湍流化等现象的演化过程,从流体粒子夹带、后缘尾迹涡面二次涡的生成、豆荚状涡对的形成及共旋卷吸等现象揭示了漩涡演化的流动特性.

[1]Mager A 1972J.Fluid Mech.55 609

[2]Devenport W J,Rife M C,Liapis S I,Follin G J 1996J.Fluid Mech.312 67

[3]Mula S M,Stephenson J H,Tinney C E,Sirohi J 2011AHS Southwest Region Technical Specialists’s MeetingFort Worth,USA,February 23–25,2011 p1

[4]Mula S M,Stephenson J H,Tinney C E,Sirohi J 2013Exp.Fluids54 1600

[5]Komerath N,Ganesh B,Wong O 200434th AIAA Fluid Dynamics Conference and ExhibitOregon,Portland,June 28–July 1,2004 p1

[6]McAlister K W 2004J.Am.Helicopter Soc.49 371

[7]Milluzzo J,Leishman J G 2016J.Am.Helicopter Soc.61 012002

[8]Jain R,Conlisk A T 2000J.Am.Helicopter Soc.45 157

[9]Widnall S E 1972J.Fluid Mech.54 641

[10]Hattori Y,Fukumoto Y 2009Phys.Fluids21 014104

[11]Hattori Y,Fukumoto Y 2012Phys.Fluids24 054102

[12]Sarmast S,Dadfar R,Mikkelsen R F,Schlatter P,Ivanell S,Sørensen J N,Henningson D S 2014J.Fluid Mech.755 705

[13]Sørensen J N 2011J.Fluid Mech.682 1

[14]Lignarolo L E M,Ragni D,Scarano F,Ferreira C J S,Bussel G J W 2015J.Fluid Mech.781 467

[15]Ali M,Abid M 2014J.Fluid Mech.740 1

[16]Mula S M,Tinney C E 2015J.Fluid Mech.769 570

[17]Hamilton N,Tutkun M,Cal R B 2016Phys.Fluids28 025103

[18]Weiss J M,Smith W A 1995AIAA J.33 2050

[19]Spalart P R 2009Annu.Rev.Fluid Mech.41 181

[20]Xiao Z X,Liu J,Huang J B,Fu S 2012AIAA J.50 1119

[21]Sirovich L 1987Quart.Appl.Math.45 561

[22]Hellström L H O,Ganapathisubramani B,Smits A J 2015J.Fluid Mech.779 701

[23]Kostas J,Soria J,Chong M S 2005Exp.Fluids38 146

[24]Luo J Q,Duan Y H,Xia Z H 2016Acta Phys.Sin.65 124702(in Chinese)[罗佳奇,段焰辉,夏振华2016物理学报65 124702]

[25]Lei P F,Zhang J Z,Wang Z P,Chen J H 2014Acta Phys.Sin.63 084702(in Chinese)[雷鹏飞,张家忠,王琢璞,陈嘉辉2014物理学报63 084702]

[26]Pan C,Wang J J,Zhang C 2009Sci.China:Phys.Mech.Astron.39 627(in Chinese)[潘翀,王晋军,张草2009 中国科学G辑:物理学力学天文学39 627]

[27]Haller G 2005J.Fluid Mech.525 1

[28]Haller G 2015Annu.Rev.Fluid Mech.47 137

[29]Cao X Q,Song J Q,Ren K J,Leng H Z,Yin F K 2014Acta Phys.Sin.63 180504(in Chinese)[曹小群,宋君强,任开军,冷洪泽,银富康2014物理学报63 180504]

[30]Caradonna F X,Tung C 19806th European Rotorcraft and Powered Lift Aircraft ForumBristol,UK,September 16–19,1980 p1