分数阶双稳系统中的非周期振动共振∗

杨建华 马强 吴呈锦 刘后广

1)(中国矿业大学机电工程学院,徐州 221116)

2)(密歇根大学机械工程系,安娜堡 MI48109,美国)

3)(中国矿业大学,江苏省矿山机电装备重点实验室,徐州 221116)

4)(河北工程大学机械与装备工程学院,邯郸 056038)

(2017年9月16日收到;2018年1月4日收到修改稿)

1 引 言

在自然科学和工程技术领域,携带有用信息的信号往往比较微弱,因此在检测和分析这些信号之前,需要先将其进行增强.增强信号的方法多种多样,其中基于非线性系统动力学理论的随机共振(stochastic resonance,SR)[1]和振动共振(vibrational resonance,VR)[2]方法近些年得到了诸多领域科研人员的广泛关注.对于简谐信号激励的系统,随机共振指的是系统输出的信噪比或谱放大因子是激励中所含噪声强度的非线性函数,通过调节噪声强度,能够使系统输出的信噪比最大,进而通过合适的噪声强度放大了输出中的微弱信号成分.在振动共振的研究中,高频辅助信号代替了噪声,通过调节高频辅助信号的幅值,能够使系统输出在特征信号频率处的响应幅值增益达到最大.然而,携带有用信息的信号不仅以周期信号的形式存在,还有大量的信息要用不同形式的非周期信号来表示,其中二进制非周期信号是一种常见的形式.在非线性系统中通过诱导系统发生非周期随机共振(aperiodic stochastic resonance,ASR)[3]或者非周期振动共振(aperiodic vibrational resonance,AVR)[4],能够增强微弱的非周期特征信息.所谓非周期随机共振或非周期振动共振,指的是当特征信号为非周期信号时,通过调节噪声强度或者高频辅助信号幅值,使得系统输出的波形和非周期特征信号的波形相似,但振幅比输入特征信号的振幅更大.目前,一般以系统输出和输入特征信号之间的相关系数作为研究非周期随机共振和非周期振动共振的指标,相关系数与噪声强度或辅助信号幅值之间呈现一条类似于“共振”的曲线,在共振点处往往会发生随机共振或者振动共振.事实上,相关系数描述的是两个时间序列之间的相似性,当相关系数取得最大值时,系统输出可能发生了非周期随机共振或者非周期振动共振,即相关系数最大是系统发生非周期随机共振或非周期振动共振的必要非充分条件.

相比于常微分形式的非线性系统,分数阶形式的非线性系统在微弱信号的动力学响应方面具有更多的优势,尤其是分数阶非线性系统能够进一步增强系统输出的随机共振[5]和振动共振[6]现象.此外,常微分系统可以看作分数阶系统的特例,因此研究分数阶系统中的随机共振和振动共振得到的结果更具有通用性.相比于随机共振,振动共振更易控制.目前虽有一些关于振动共振的研究文献,但是分数阶系统中的非周期振动共振问题还尚未研究,考虑到分数阶系统动力学行为的丰富性以及非周期信号的广泛存在性,研究这一问题具有重要意义.

本文分以下几部分展开研究:第2部分研究分数阶系统中的经典非周期振动共振现象,即系统参数和信号参数能够直接实现匹配,参数不需要进行其他方面的处理;第3部分和第4部分研究系统参数和信号参数不能直接匹配的情况,即非周期信号的脉宽具有任意小值的情况,实现系统参数和信号参数的匹配才能诱发振动共振现象;这两部分分别使用了变尺度法和二次采样法,通过这两种不同的方法,分别实现系统参数和信号参数的匹配,诱发非周期振动共振,达到殊途同归的效果;第5部分对本文的主要结果进行总结.

2 非周期振动共振

研究模型如下:

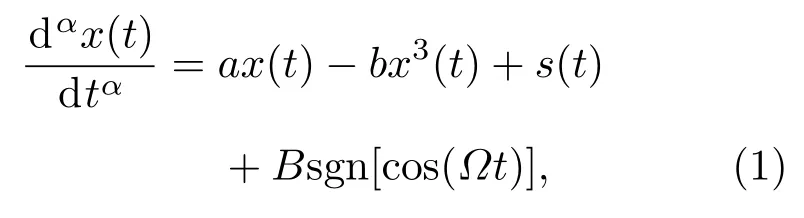
其中a＞0,b＞0为系统参数,系统为具有双稳态势函数的分数阶系统.分数阶导数采用Grünwald-Letnikov定义[7],即

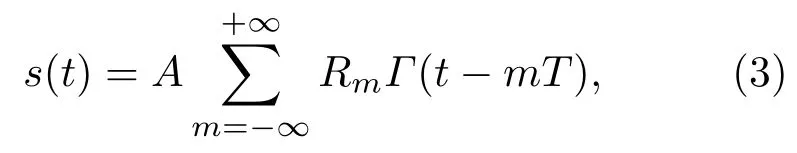
其中A为二进制非周期信号的振幅,Rm=±1为符合高斯分布的随机数,T为脉宽,即s(t)中的最小随机脉冲的宽度.Bsgn[cos(Ωt)]为诱发振动共振使用的辅助信号,辅助信号的幅值和周期分别为B和2π/Ω.根据振动共振理论,一般要求辅助信号随时间的变化远快于特征信号的变化[2],因此有2π/Ω≪T,本文令Ω=2π/(βT),其中β≫1.对于特征信号是简谐信号的情况,辅助信号一般也以简谐信号的形式表示.对于辅助信号是非周期信号的情况,Chizhevsky和Giacomelli[4]采用了如(1)式中的周期方波作为辅助信号.根据动力学理论,特征信号影响系统输出中的慢变成分,辅助信号影响系统输出中的快变成分,辅助信号的作用是改变等效系统的参数,即改变等效系统势函数的形状,进而影响输出中慢变成分的动力学行为[8−10].辅助信号的形式不同,不会对结果造成本质的影响,本文选取(1)式中方波信号作为辅助信号.再者,周期方波表达式可具有多种不同的形式,使用(1)式中的形式,在数值编程计算方面更简单.

对于非周期信号,可以采用相关系数作为指标来度量振动共振现象.根据相关系数的物理意义,相关系数取值越大,表示两个时间序列之间的相似性越高,当相关系数为1时,两个时间序列完全相似.当发生振动共振时,系统输出的时间序列与输入信号之间的相关系数达到最大值.反之,当相关系数最大时,系统的输出未必发生了振动共振.换句话说,相关系数最大是发生振动共振的必要非充分条件,后续分析将给予必要的说明.系统输出的时间序列与输入信号之间的相关系数用Csx表示,其具体的计算表达式为

为帮助读者更好地理解,图1给出了二进制非周期信号的三种不同波形.即使信号的振幅和脉宽相等,由于Rm的随机性,特征信号的时间序列也是不同的.

图1 相同幅值和脉宽下二进制非周期信号的三种不同波形(A=0.3,T=20)Fig.1.Three different waveforms of the binary aperiodic signal under the same signal amplitude and pulse width(A=0.3,T=20).

图2 特征信号波形以及系统阶数α取值不同时,相关系数Csx与辅助信号幅值B之间的关系(仿真参数为a=1,b=1,A=0.3,T=20,β=10) (a)α=0.4;(b)α=0.7;(c)α=1.0;(d)α=1.5Fig.2.Curves of Csx-B are obtained under different waveforms of the character signal and different fractional order values.The simulation parameters are a=1,b=1,A=0.3,T=20 and β=10:(a)α=0.4;(b)α=0.7;(c)α=1.0;(d)α=1.5.

图3 系统阶数取值不同时的最佳非周期振动共振输出 (a)α=0.4,B=0.75;(b)α=0.7,B=1.2;(c)α=1.0,B=1.45;(d)α=1.5,B=1.55;其他仿真参数为a=1,b=1,A=0.3,T=20,β=10;红色粗实线为输入的特征信号;黑线虚线对应B=0的输出;蓝色线细实线为最佳非周期振动共振输出Fig.3.The optimal AVR output corresponding to different fractional-order values:(a) α =0.4,B=0.75;(b)α=0.7,B=1.2;(c)α=1.0,B=1.45;(d)α=1.5,B=1.55.Other simulation parameters are a=1,b=1,A=0.3,T=20 and β=10.Thick lines in red color is the input character signals;dashed lines in black color is the output corresponding to B=0;thin lines in blue color is the optimal AVR output.

针对图1中的三种不同波形的信号,图2分别给出了系统的阶数α不同时,系统输出与特征信号之间的相关系数随着辅助信号幅值变化的曲线,其中的信号1(signal 1),信号2(signal 2),信号1(signal 3)分别对应图1中从上至下的三种信号.后续对不同信号的类似描述,均采用相同的方法.图2中给出了几种重要现象.第一,Csx与B之间的关系曲线基本不受输入信号波形的影响.由于相关系数是基于大数据量进行计算的统计特征参数,提高计算使用的数据量,能够进一步减小特征信号波形不同造成的Csx-B曲线的微小误差.第二,随着辅助信号的幅值增加,Csx的值先减小后增大,出现了明显的“共振区”,即发生非周期振动共振现象.“共振区”是描述线性系统在简谐激励下响应特性的指标,一般将频响曲线上位于共振峰值的两侧并满足大于共振峰值的的区域定义为“共振区”[11,12].对于非周期振动共振,并没有“共振区”的统一概念,为方便描述,仿照简谐激励下线性系统“共振区”的概念,本文将Csx-B曲线上位于波谷右侧且位于共振峰值两侧并满足Csx大于共振峰值的倍的区域定义为非周期振动共振的“共振区”.在B取值较小时,相关系数Csx的值较大,这说明输出时间序列和输入信号的相似性较高,但输出时间序列中的特征信号部分并未得到放大.在各个曲线的共振点,输出时间序列和输入特征信号之间的相似性高,且输出时间序列中含有的特征信号成分得到了放大,后续对时间序列的分析中将说明这一点.第三,随着系统阶数的增加,Csx-B曲线的“共振区”变宽,且发生最佳振动共振时所需要辅助信号的幅值变大.

对应于图2中信号2的最佳共振点,图3给出了系统阶数取值不同时的最佳非周期振动共振输出.相对于原信号,系统输出中的特征信号波形在很大程度上得到了增强.在图3的4个子图中,系统阶数的取值越大,系统输出和输入特征信号之间的相似程度越高.对于B=0,即激励中不含有辅助信号的情况,虽然系统的输出与输入特征信号之间相似程度高,但是特征信号未得到明显的放大.这一现象验证了对于图2的第二条解释,即相关系数取值大是发生非周期振动共振的必要非充分条件.

为进一步验证分数阶双稳态系统的非周期振动共振现象,图4给出了特征信号的振幅A取值不同时的非周期振动共振曲线.对于不同的A值,Csx-B曲线都呈现明显的非周期振动共振现象;A的取值越大,Csx-B曲线发生振动共振时的峰值越大.此外,特征信号的振幅越大,发生最佳非周期振动共振时所对应的高频辅助信号的幅值越小.

图4 特征信号幅值以及系统阶数α取值不同时,相关系数Csx与辅助信号幅值B之间的关系(仿真参数为a=1,b=1,T=20,β=10) (a)α=0.4;(b)α=0.7;(c)α=1.0;(d)α=1.5Fig.4.Curves of Csx-B are obtained under different amplitudes of the character signal and different fractional-order values.The simulation parameters are a=1,b=1,T=20 and β=10:(a)α=0.4;(b)α=0.7;(c)α=1.0;(d)α=1.5.

图5给出了非周期信号脉宽取值不同时,Csx-B曲线所呈现的非周期振动共振现象.随着T的增大,Csx-B曲线的共振峰值变大,且“共振区”变窄,这与常规频率响应曲线所呈现的规律类似,较易理解.同时,系统阶数所呈现出来的影响规律和其他图形中的相关规律类似.当然,图中使用的非周期信号脉冲宽度的取值不能太小,否则非周期振动共振会消失,需要其他的方法来诱导振动共振,这正是本文第3和第4部分要讨论的内容.

结合以上图形进行分析,系统阶数对振动共振的影响主要表现在两个方面:一方面,随着阶数α的变大,Csx-B曲线发生共振时对应的B值变大,如图2,图4和图5所示.这个现象可以从振动共振发生的本质原因来理解,振动共振的发生是因为辅助的快变信号作用于非线性系统,其作用相当于改变了非线性系统的参数,即等效的非线性系统参数是辅助信号振幅的函数,随着辅助信号振幅的增大,等效非线性系统的平衡点数目将发生变化.对于本文的双稳系统,辅助信号幅值的增加将会使等效系统由双稳态变为单稳态,使系统发生了叉形分岔,叉形分岔是引起振动共振的根本原因[6].对于外激励都是简谐信号的情况,可以用快慢变量分离法求得发生叉形分岔的临界B值[8,9],且随着阻尼阶数的增加,引起叉形分岔的临界B值将增大,这在以往振动共振的相关文献中都有描述.(1)式中的激励均为非简谐信号,但振动共振发生的机理不变,快变形式的辅助信号仍引起等效系统的叉形分岔,且系统阶数越大,引起叉形分岔的临界B值就越大,导致发生共振时需要的B值也变大.另一方面,从时间序列上直观分析,系统阶数对时间序列的形状也会有影响,如在图3中所给定的几种α取值情况下,随着α的增大,输出时间序列的形状与二进制非周期信号之间的相似性明显增加,这可以从系统的响应特性方面来理解.对于二进制非周期信号,在信号的转折点处,即信号由负(正)值变为正(负)值的转折点,相当于对系统输入一个短时的阶跃信号,而系统在二进制非周期信号转折点处一定时间内的响应是系统瞬态响应、该短时阶跃信号引起的稳态响应以及辅助信号引起的响应共同作用的结果,因为考虑的是系统输出与二进制非周期信号的相似性,在这些响应成分中,短时阶跃响应引起的系统响应起主要作用.上升时间是度量系统响应特性的重要指标[13,14],上升时间越快,系统响应达到和输入信号相似所需要的时间就越短,相似性就越好.从图3可以看出,随着α的增大,系统输出和二进制非周期信号之间的相似性也增加,在相关系数方面应该表现为相关系数变大.这一点在图4中表现更为明显,图4中对应A=0.1的曲线,可以明显地看到随着α的增大,Csx-B曲线的共振峰值变大,即发生共振时的最大相关系数的值变大,也即系统输出的时间序列和输入的二进制非周期信号之间的相似性变好.总之,非周期振动共振是一种比较复杂的非线性动力学现象,其动力学特性是多种因素共同作用的结果,可以主要从以上两方面来理解系统阶数对非周期振动共振的影响.

图5 特征信号脉宽以及系统阶数α取值不同时,相关系数Csx与辅助信号幅值B之间的关系(仿真参数为a=1,b=1,β=10) (a)α=0.4;(b)α=0.7;(c)α=1.0;(d)α=1.5Fig.5.The curves of Csx-B are obtained under different pulse width of the character signal and different fractionalorder values.The simulation parameters are a=1,b=1 and β=10:(a)α=0.4;(b)α=0.7;(c)α=1.0;(d)α=1.5.

3 基于变尺度法的非周期振动共振

为说明本部分所阐述的问题,首先给出一组二进制非周期信号,该信号和图1中对应的信号具有完全相似的波形,但是时间尺度不同,即脉宽的大小不同.相对于图1中脉宽的取值,图6中的脉宽缩小为图1中脉宽的百分之一.通俗地讲,可以认为图1中的特征信号是慢变信号,而图6中的特征信号是快变信号.快变特征信号在工程应用中也是广泛存在的,因此研究快变特征信号的振动共振问题具有理论意义和工程价值.

在图6的三种不同波形的二进制非周期信号激励下,直接研究非周期振动共振现象,结果如图7所示.在图7中,振动共振现象消失,不能再利用振动共振实现二进制非周期信号的放大.究其原因,是因为系统参数和信号达不到应有的匹配.相比于图1中的信号,图6中的信号脉冲宽度缩小,而所使用的系统未发生变化,因此不能诱导振动共振的发生,只有信号参数和系统参数重新达到匹配才能解决这一问题.我们以变尺度法实现信号和系统的匹配变尺度法在高频简谐信号激励下系统的随机共振[15,16]以及振动共振[17,18]的研究中已经取得了很好的效果,并应用于解决工程实际问题.

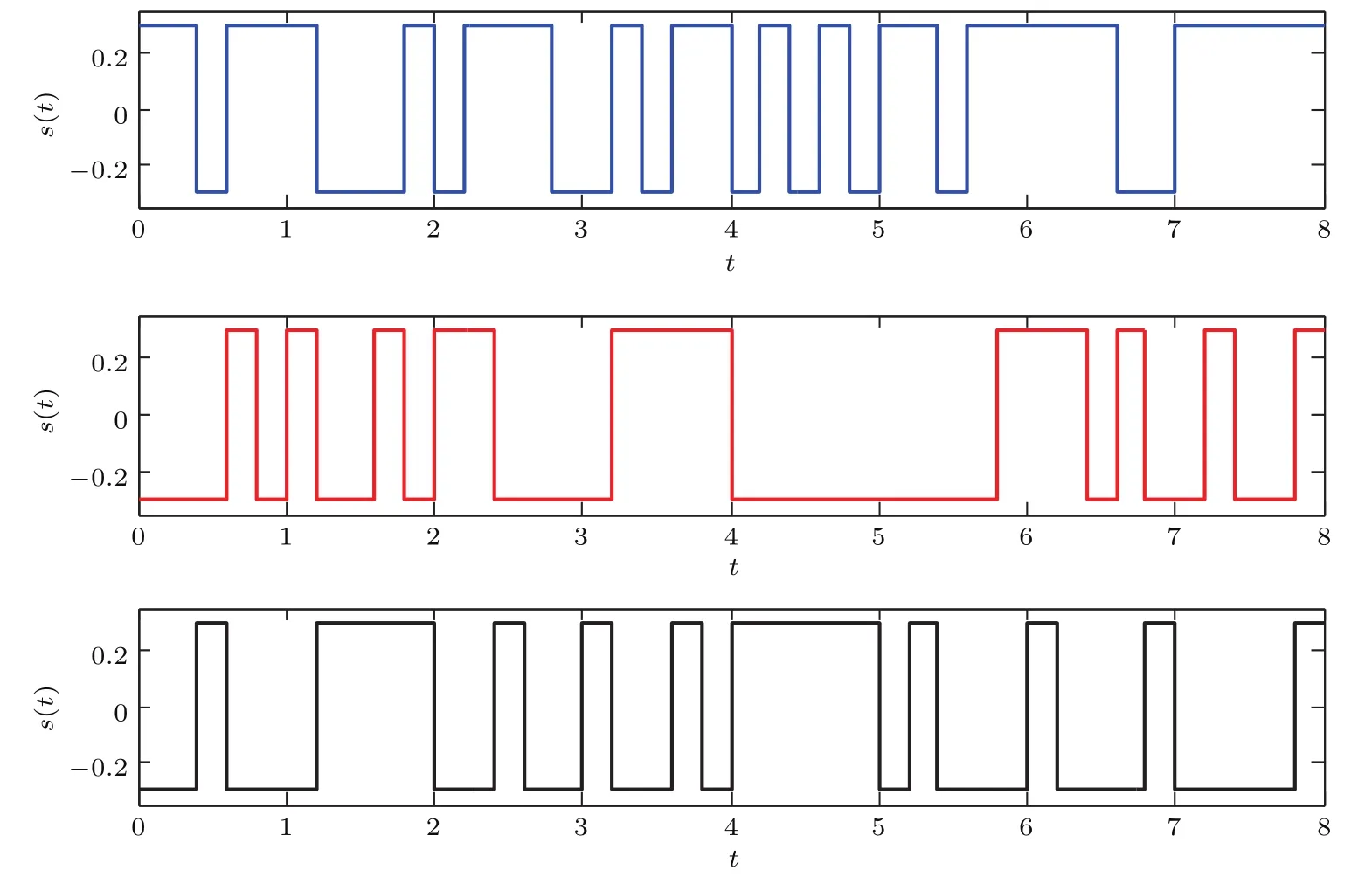
图6 相同幅值和脉宽下二进制非周期信号的三种不同波形(A=0.3,T=0.2)Fig.6.Three different waveforms of the binary aperiodic signal under the same signal amplitude and pulse width(A=0.3,T=0.2).

首先,引入尺度变换

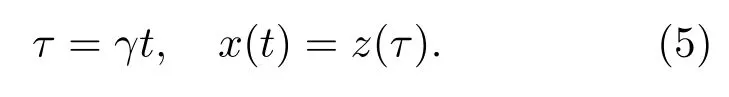
把(5)式代入(1)式并根据分数阶导数尺度变换的性质[19],得到

令

则

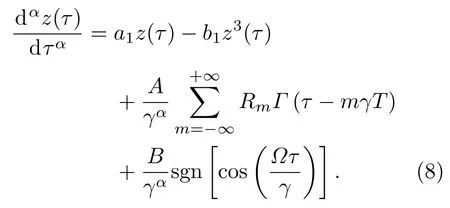
对比(8)式和(1)式,非周期信号的脉宽被放大了γ倍,能够将快变信号变为慢变信号,同时辅助信号也进行了相应的频率变换,能够匹配特征信号.因此,经过尺度变换后,(8)式中的激励信号与(1)式中的激励信号具有了相同的时间尺度,即都为慢变信号.此外,选择合适的γ,使(8)式中的系统参数a1和b1可以具有与(1)式中的系统参数a和b相同的值或者相同量级的值.所以,系统(1)达到振动共振的匹配条件时,即信号参数和系统参数相匹配时,(8)式中的信号参数和系统参数可以对照(1)式来选取.同时还要注意到,(8)式和(1)式相比,激励信号的振幅都缩小为原来的1/γα.因此,在时间尺度τ中与(1)式等价的方程应为综合以上分析过程,在时间尺度t中要实现快变特征信号的非周期振动共振,应该在以下方程中求解:

图7 特征信号波形以及系统阶数α取值不同时,相关系数Csx与辅助信号幅值B之间的关系(仿真参数为a=1,b=1,A=0.3,T=0.2,β=10) (a)α=0.4;(b)α=0.7;(c)α=1.0;(d)α=1.5Fig.7.The curves of Csx-B are obtained under different waveforms of the character signal and different fractionalorder values.The simulation parameters are a=1,b=1,A=0.3,T=0.2 and β=10:(a)α=0.4;(b)α=0.7;(c)α=1.0;(d)α=1.5.

图8 变尺度条件下相关系数Csx与辅助信号幅值B之间的关系曲线 (仿真参数为a1=1,b1=1,A=0.3,T=0.2,β=10,γ=100) (a)α=0.4;(b)α=0.7;(c)α=1.0;(d)α=1.5Fig.8.The curves of Csx-B are obtained by the re-scaled method.The simulation parameters are a1=1,b1=1,A=0.3,T=0.2,β=10 and γ=100:(a)α=0.4;(b)α=0.7;(c)α=1.0;(d)α=1.5.

在以上分析中,a1,b1都是小参数,一般都是1的量级,γ根据如何把快变特征信号变为慢变信号来设定大小.以下用算例进行分析验证.

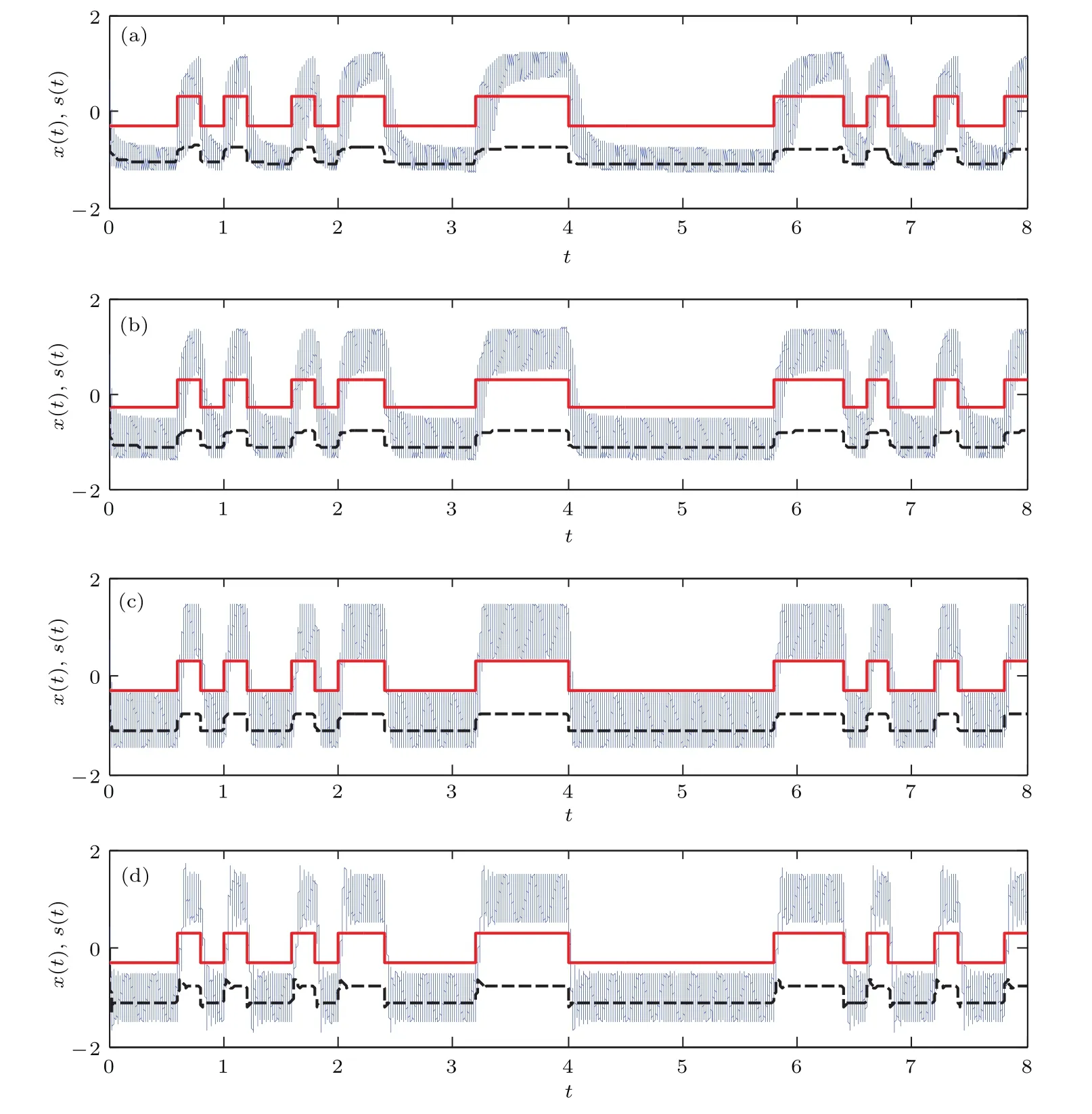
图9 变尺度条件下的最佳非周期振动共振输出 (a)α=0.4,B=0.75;(b)α=0.7,B=1.2;(c)α=1.0,B=1.5;(d)α=1.5,B=1.6;其他仿真参数为a=1,b=1,A=0.3,T=20,β=10,γ=100;红色粗实线为输入的特征信号;黑线虚线对应B=0的输出;蓝色细实线为最佳非周期振动共振输出Fig.9.The optimal AVR output time series are obtained by the re-scaled method:(a)α=0.4,B=0.75;(b)α=0.7,B=1.2;(c)α=1.0,B=1.5;(d)α=1.5,B=1.6.Other simulation parameters are a=1,b=1,A=0.3,T=20,β =10 and γ =100.Thick lines in red color is the input character signals;dashed lines in black color is the output corresponding to B=0;thin lines in blue color is the optimal AVR output.

针对图6中三种波形的二进制信号,图8中采用变尺度法实现了非周期振动共振现象显然,基于(10)式实现了图6中的信号与图8中所采用系统参数的匹配通过γ=100的尺度变换,相当于把特征信号T=0.2的脉宽变换到与特征信号T=20的脉宽等价的系统中,因此图8中的Csx-B曲线与图2中对应的曲线形状基本相同,这也说明了变尺度后(10)式与(1)式的等价性.使用变尺度法能够在分数阶非线性系统中实现快变特征信号(本文中是指脉宽取值小的情况)的非周期振动共振,且不受脉冲宽度及信号波形的影响.

根据图8中的曲线,在图9中给出了变尺度条件下特征信号(信号2)的最佳振动共振输出.首先,非周期信号在脉宽比较小的情况下实现了振动共振现象,特征信号得到了放大.其次,对比图9和图3,发现系统发生非周期振动共振时输出的波形以及对应辅助信号的幅值B基本相同,些许的小误差可以认为由数值计算所引起.从图9的时间序列上再一次说明了变尺度法处理非周期快变特征信号的有效性以及变尺度后(10)式与(1)式的等价性.

为进一步说明变尺度法的有效性,图10中在脉宽T取值不同时给出了对应于系统阶数不同取值的Csx-B曲线.图10中的曲线与图5中的对应曲线基本相同,这是因为采用变尺度法后,在γ=100的条件下,脉宽T=0.1,T=0.15,T=0.2在等效的系统中分别变为T=10,T=15,T=20.因此,图10中的曲线与图5中的对应曲线基本相同.

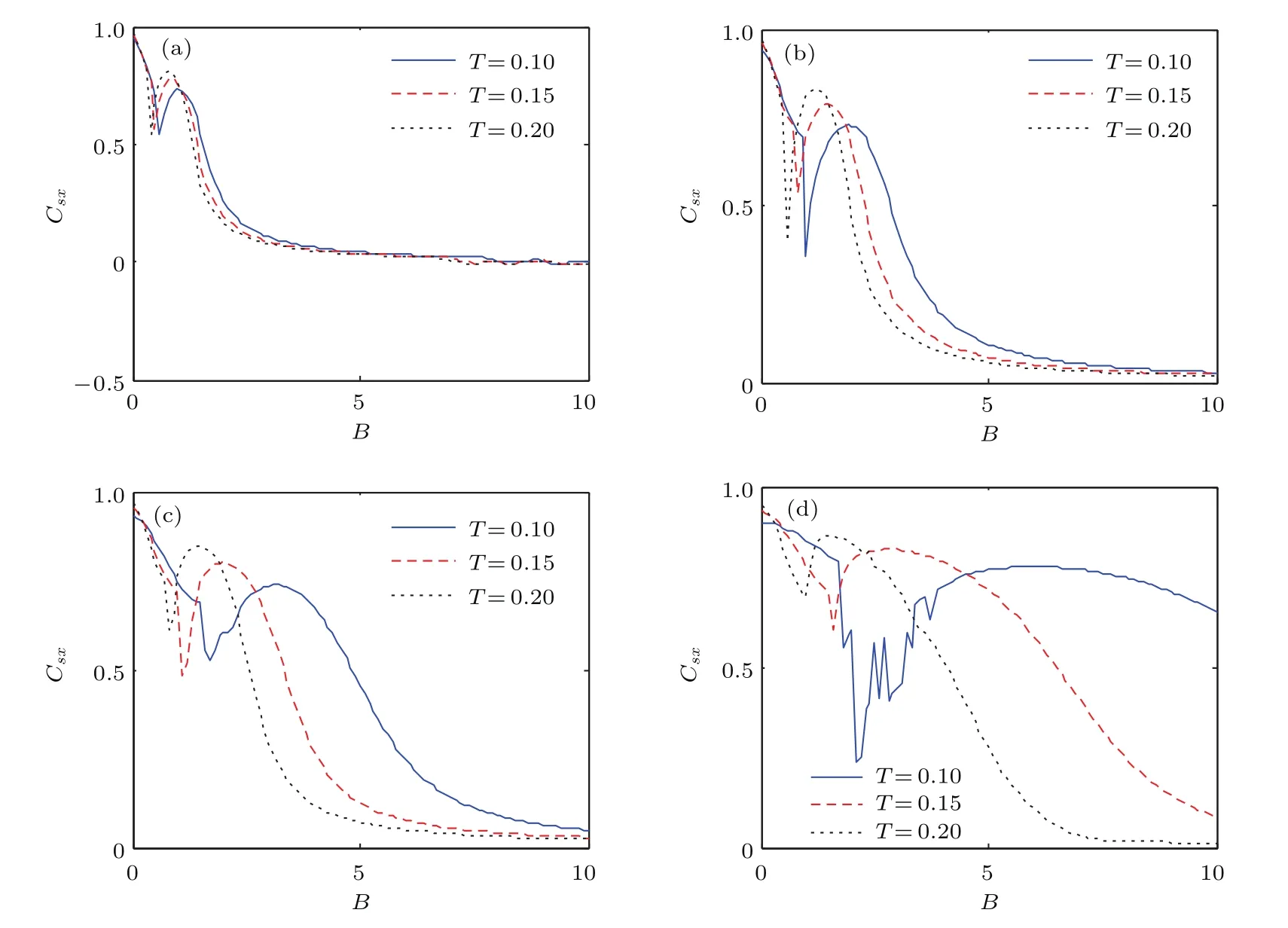
图10 变尺度条件下相关系数Csx与辅助信号幅值B之间的关系 (仿真参数为a1=1,b1=1,A=0.3,β=10,γ=100) (a)α=0.4;(b)α=0.7;(c)α=1.0;(d)α=1.5Fig.10.The curves of Csx-B are obtained by the re-scaled method.The simulation parameters are a1=1,b1=1,A=0.3,β=10 and γ=100:(a)α=0.4;(b)α=0.7;(c)α=1.0;(d)α=1.5.

图11中在不同的尺度系数下给出了Csx-B曲线.图11中的曲线与图10以及图2中的对应曲线基本一致,这是因为在所选的尺度系数下,等效的脉宽又分别变为T=10,T=15,T=20.因此,出现图11中的曲线与图10以及图2中的对应曲线基本一致的情况.在图8—图11中,通过选取不同的信号波形以及不同的特征信号参数和变尺度系数,验证了变尺度法实现分数阶系统中非周期振动共振的有效性,这种方法使得信号参数和系统参数能够实现较好的匹配,非周期振动共振的发生不再依赖于脉宽的情况.在任何脉宽情况下,都可以使用该方法诱发非周期振动共振.

图11 变尺度条件下相关系数Csx与辅助信号幅值B之间的关系(仿真参数为a1=1,b1=1,A=0.3,T=0.2,β=10) (a)α=0.4;(b)α=0.7;(c)α=1.0;(d)α=1.5Fig.11.The curves of Csx-B are obtained by the re-scaled method.The simulation parameters are a1=1,b1=1,A=0.3,T=0.2 and β=10:(a)α=0.4;(b)α=0.7;(c)α=1.0;(d)α=1.5.

4 基于二次采样法的非周期振动共振

除变尺度法之外,二次采样法在基于动力学的共振原理处理高频信号方面也具有良好的效果.二次采样法由冷永刚教授等首先提出[20],并应用于工程问题的研究[21,22].二次采样法的步骤如下:

1)对激励信号确定第一次采样的频率fs,并进行第一次采样;

2)对第一次采样后的离散信号进行第二次采样,二次采样频率为fs/κ,通过二次采样,信号进行了重构激励信号周期(或脉宽)变为原来的κ倍,κ可以称为二次采样频率比,基于此原理能够将快变特征信号变换成慢变信号;

3)将经过二次采样重构的信号输入到非线性系统,系统参数不必进行变化,仍采用小参数系统,而后得到输出的时间序列;

4)根据第一次采样频率的数值以及二次采样频率比进行逆变换,将系统的输出再变回到第一次采样频率下的时间序列;

5)根据计算指标,对上一步的时间序列进行分析,得出结果.

针对图6中的信号,在图12中给出了基于二次采样法得到的Csx-B曲线.在该图中,振动共振现象明显,这说明二次采样法的有效性.图12中的曲线和图8中的曲线基本一致,这说明用二次采样法和变尺度法实现非周期振动共振的等效性.

二次采样法和变尺度法在实现快变信号的非周期振动共振方面有异曲同工之妙,但其物理过程是不同的.变尺度法是对系统参数,即系统的尺度进行变换,信号振幅相应地放大,信号的频率或者脉宽不变,用变化后的系统去匹配原信号,实现振动共振.二次采样法是对输入的信号进行变换,通过二次采样将快变特征信号变为慢变信号,系统不发生变换,用变换后的信号去匹配原系统,实现振动共振.在工程应用中,应该根据实际的物理条件来选择所需要的方法.

5 结 论

以二进制非周期信号为特征信号,以周期方波信号为辅助信号,以相关系数为指标,研究了分数阶双稳系统中的非周期振动共振现象.主要得到了以下结论.

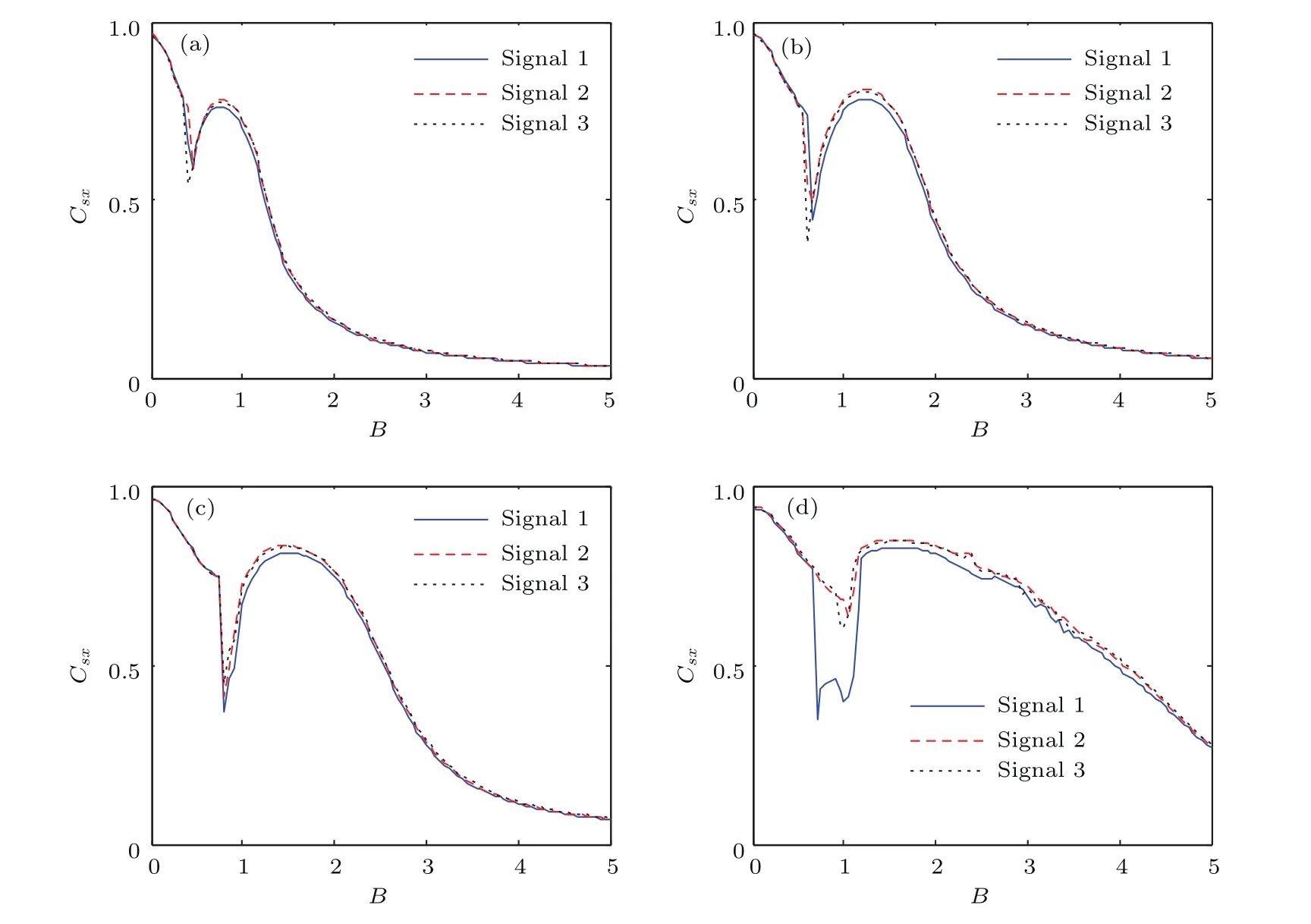
图12 基于二次采样法得到的相关系数Csx与辅助信号幅值B之间的关系(仿真参数为a=1,b=1,A=0.3,T=0.2,β=10,κ=100) (a)α=0.4;(b)α=0.7;(c)α=1.0;(d)α=1.5Fig.12.The curves of Csx-B are obtained by the twice sampling method.The simulation parameters are a=1,b=1,A=0.3,T=0.2,β=10 and κ=100:(a)α=0.4;(b)α=0.7;(c)α=1.0;(d)α=1.5.

1)当特征信号为慢变信号时,即脉宽较大的情况,系统参数为小参数即可满足系统和信号的匹配,通过调节辅助信号的幅值,能够诱发非周期振动共振,进而增强特征信号.

2)当特征信号为快变信号,即脉宽较小的情况,需要一定的技术方法才能实现系统参数和信号参数的匹配去诱发振动共振,本文给出了两种相关方法:第一种方法是变尺度法,通过尺度变换,得到与原系统等效的新系统,实质上是变换了系统的尺度,使新系统的参数和原信号参数达到匹配,从而诱发非周期振动共振,在该方法的使用过程中,变尺度系数是起决定性作用的关键因素;第二种方法是二次采样法,通过对输入信号进行二次采样,得到的新信号可与原系统参数进行匹配,进而能够诱发非周期振动共振,在该方法的使用过程中,二次采样频率比是起决定性作用的关键因素.

3)系统的阶数对响应的动力学行为有重要的影响.随着系统阶数的增大,相关系数与辅助信号幅值之间的曲线所呈现的共振区域变宽,诱发最佳振动共振所需要的辅助信号幅值变大,在时间序列上表现为输出的时间序列与输入的特征信号之间的相似性增强.

本文实现了二进制非周期信号在不同脉宽下的非周期振动共振现象,可对非周期信号的增强及检测提供参考思路.同时,也给出了分数阶非线性系统在非周期激励下的一些典型的非线性动力学行为,对分数阶系统的研究具有参考价值.

[1]Gammaitoni L,Hänggi P,Jung P,Marchesoni F 1998Rev.Mod.Phys.70 223

[2]Landa P S,McClintock P V 2000J.Phys.A:Math.Gen.33 L433

[3]Collins J J,Chow C C,Capela A C,ImhoffT T 1996Phys.Rev.E54 5575

[4]Chizhevsky V N,Giacomelli G 2008Phys.Rev.E77 051126

[5]Yang J H,Sanjuán M A F,Liu H G,Litak G,Li X 2016Commun.Nonlinear Sci.Numer.Simulat.41 104

[6]Yang J H 2017Bifurcation and Resonance in Fractionalorder Systems(Beijing:Science Press)(in Chinese)[杨建华2017分数阶系统的分岔与共振(北京:科学出版社)]

[7]Monje C A,Chen Y Q,Vinagre B M,Xue D,Feliu V 2010Fractional-order Systems and Controls(London:Springer)p11

[8]Blekhman I I 2000Vibrational Mechanics(Singapore:World Scientific)

[9]Thomsen J J 2003Vibrations and Stability:Advanced theory,Analysis,and Tools(Berlin:Springer-Verlag)pp287–334

[10]Thomsen J J 2002J.Sound Vib.253 807

[11]Balachandran B,Magrab E B 2008Vibrations(Australia:Cengage Learning)pp210–212

[12]Hu H Y 2004Foundation of Mechanical Vibration(Harbin:Harbin Institute of Technology Press)p26(in Chinese)[胡海岩 2004机械振动基础 (哈尔滨:哈尔滨工业大学出版社)p26]

[13]Palm W J 2005System Dynamics(2nd Ed.)(New York:McGraw-Hill Higher Education)p498

[14]Ogata K 2004System Dynamics(4th Ed.)(New Jersey:Prentice Hall)pp384–388

[15]Liu X,Liu H,Yang J,Litak G.,Cheng G,Han S 2017Mech.Sys.Signal Pr.96 58

[16]Huang D,Yang J,Zhang J,Liu H 2017P.I.Mech.Eng.C-J.Mec.doi:0954406217719924

[17]Yang J H,Sanjuán M A F,Liu H G 2017J.Comput.Nonlin.Dyn.12 051011

[18]Liu H G,Liu X L,Yang J H,Sanjuán M A F,Cheng G 2017Nonlinear Dynam.89 2621

[19]Magin R,Ortigueira M D,Podlubny I,Trujillo J 2011Signal Process.91 350

[20]Leng Y G,Wang T Y 2003Acta Phys.Sin.52 2432(in Chinese)[冷永刚,王太勇 2003物理学报 52 2432]

[21]Leng Y G,Wang T Y,Guo Y,Xu Y G,Fan S B 2007Mech.Syst.Signal Pr.21 138

[22]Li Q,Wang T,Leng Y,Wang W,Wang G 2007Mech.Syst.Signal Pr.21 2267