基于小波神经网络的数字信号调制方式识别

梁 晔, 郝 洁, 石 蕊

(1. 兰州城市学院 电子与信息工程学院, 兰州 730070; 2. 西北民族大学 电气工程学院, 兰州 730030)

在数字信号应用过程中, 信号的调制解调技术十分关键, 在数字信号进行解调时, 首先要知道数字信号的调制方式, 因此数字信号调制方式自动、 快速准确识别的研究受到广泛关注[1-6].

数字信号调制方式的识别最初采用人工方式实现, 首先通过具有相关知识的专业人员设置不同类型的解调器, 然后对接收到的数字信号进行变频处理, 将变频后的信号输入到解调器中, 最后结合自己的知识、 波形以及声音得到数字信号调制方式. 该方法由于需要人工参与, 自动化程度低, 同时数字信号调制方式识别结果与专业人员自身知识密切相关, 导致数字信号调制方式识别正确率较低, 而且数字信号调制方式识别时间长, 无法满足数字信号发展的要求[7-8]. 随着数字信号和信息处理技术的不断完善, 目前已有许多新的数字信号调制方式自动识别方法, 如: 基于混沌理论的数字信号调制方式识别方法, 对数字信号进行混沌分析, 通过模式识别技术实现数字信号调制方式识别； 基于星座图的数字信号调制方式识别方法； 基于小波分析的数字信号调制方式识别方法; 基于高阶累积量的数字信号调制方式识别方法等. 这些方法在数字信号的信噪比较高时, 可获得较理想的数字信号调制方式识别结果[9-11], 但当信噪比减小时, 数字信号调制方式识别正确率急剧下降[12-13]. 文献[14-16]提出了基于BP神经网络的数字信号调制方式识别方法, 由于BP神经网络属于智能学习算法, 可对数字信号调制方式进行自动分类, 提高了数字信号调制方式的识别正确率, 但BP神经网络自身存在易陷入局部极小值等缺陷, 会对数字信号调制方式识别产生不利影响. 小波神经网络是小波理论和神经网络相结合的产物, 比其他神经网络具有更优的自组织、 自学习和容错能力, 为数字信号调制方式识别的建模提供了一种新工具.

针对目前数字信号调制方式识别方法存在正确率低等缺陷, 本文提出一种基于小波神经网络的数字信号调制方式识别方法. 首先从数字信号中提取调制方式识别的特征, 然后采用小波神经网络建立数字信号调制方式识别的分类器, 最后在MATLAB2016平台上实现数字信号调制方式识别的仿真测试. 实验结果验证了小波神经网络数字信号调制方式识别的有效性和优越性.

1 小波神经网络的数字信号调制方式识别流程

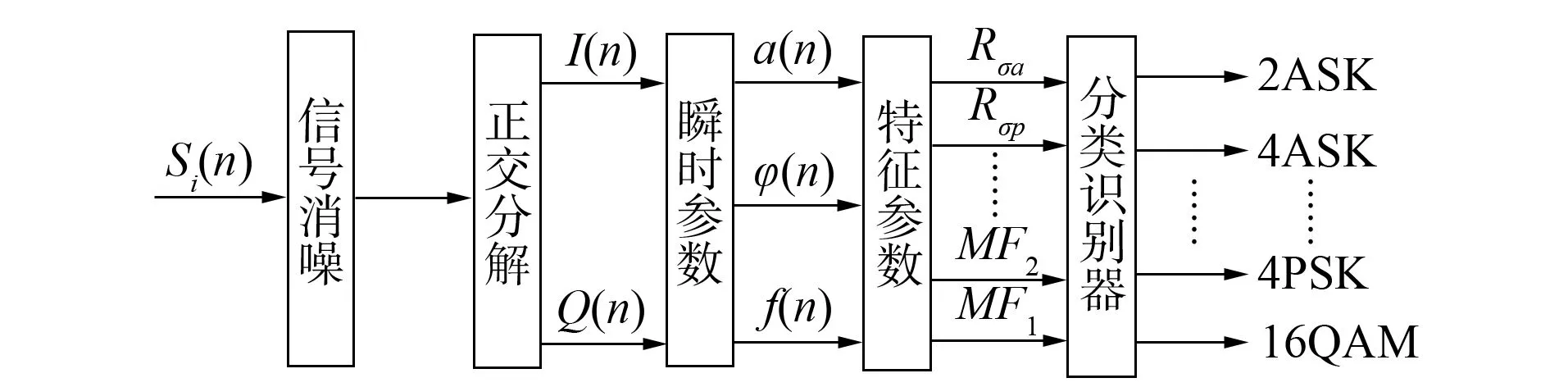
图1 数字信号调制方式的识别流程Fig.1 Identification process of digital signal modulation mode

基于小波神经网络的数字信号调制方式识别方法工作流程可分为如下3个阶段：

1) 采集数字信号, 并对信号进行预处理, 主要为信号的消噪处理;

2) 提取数字信号调制方式识别的特征参数;

3) 设计数字信号调制方式识别的分类器.

基于小波神经网络的数字信号调制方式识别流程如图1所示.

2 基于小波神经网络的数字信号调制方式识别方法设计

2.1 数字信号的预处理

设包含有噪声的数字信号为x(t)=s(t)+n(t), 其中s(t)和n(t)分别表示原始信号和噪声, 对x(t)进行变换可得

wx(j,k)=ws(j,k)+wn(j,k),j=0,1,…,J;k=0,1,…,N,

(1)

其中:wm(j,k)(m=x,s,n)表示第j层上的不同信号变换系数；J表示分解层数；N表示信号大小.

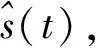
(2)

其中sgn( )表示符号函数.

2.2 提取数字信号的特征参数

目前数字信号调制方式识别特征参数较多, 由于信号瞬时信息可更好描述数字信号调制方式的类型, 因此提取信号瞬时信息的6个特征参数:

1) 数字信号幅度的标准差和均值分别为σa和ua,Rσa为两者的比值, 计算公式为

(3)

2) 数字信号的相位标准差和均值分别为σp和up, 其比值为Rσp, 计算公式为

(4)

3)A表示数字信号的零中心归一化瞬时幅度, 平均值M2的计算公式为

(5)

4)Af表示数字信号的零中心归一化瞬时频率,

其中,af表示信号的瞬时频率; 均值MF1计算公式为

(6)

(7)

6)Af的相位为Ap, 均值MP1计算公式为

(8)

2.3 粒子群优化小波神经网络

2.3.1 粒子群优化算法 设粒子的位置和速度分别为Xi和Vi, 在解空间中, 粒子的位置更新通过不断跟踪自身最优解Pbest=(pi1,pi2,…,piD)和群体最优解Gbest=(pg1,pg2,…,pgD)实现, 计算公式为

Vid=ω×Vid+c1×rand( )×(Pbest-xid)+c2×rand( )×(Gbest-xid),

(9)

Xid=Xid+Vid,

(10)

图2 小波神经网络结构Fig.2 Structure of wavelet neural network

其中: rand( )表示随机数;d表示维数;c1和c2表示加速系数；ω表示权值.

2.3.2 小波神经网络 本文采用小波基函数代替隐含层激活函数产生小波神经网络, 通过小波神经网络对数字信号调制方式进行学习, 建立数字信号调制方式的分类器, 数字信号调制方式识别的小波神经网络结构如图2所示.

小波函数可定义为

(11)

小波神经网络的隐含层第j个神经元的输入和输出分别为

(12)

其中：ωij表示输入层与隐含层间的连接权值；θj(k)表示隐含层的阈值. 小波神经网络的输出层第j个神经元的输入和输出分别为

(14)

(15)

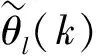
(16)

小波神经网络的数字信号调制方式识别步骤如下:

1) 采集数字信号, 并通过阈值法去除数字信号中的噪声;

2) 从去除噪声的数字信号中提取信号瞬时信息的6个特征参数, 并做归一化处理

(17)

3) 根据信号瞬时信息的6个特征参数确定小波神经网络的拓扑结构, 并初始化小波神经网络相关参数;

4) 确定粒子群的适应度函数, 将数字信号调制方式识别平均误差作为粒子群优化小波神经网络参数的适应函数值, 公式为

(18)

其中:di和tk分别表示数字信号调制方式识别类型和实际的数字信号调制方式;m表示小波神经网络的输出节点数量；n表示数字信号调制方式的训练样本数量;

5) 将数字信号调制方式识别的训练样本输入到小波神经网络进行学习, 并通过粒子群优化算法优化小波神经网络的权值和阈值;

6) 根据新的粒子群适应度值对当前数字信号调制方式识别分类器参数最优解进行不断更新;

7) 当找到数字信号调制方式识别分类器参数的最优解时, 粒子群算法寻优结束;

8) 小波神经网络根据最优权值和阈值对数字信号调制方式识别的训练样本进行重新学习, 建立最优的数字信号调制方式识别分类器;

9) 将待测试的数字信号调制方式识别样本输入到分类器中进行学习, 并输出该数字信号调制方式的类型.

3 仿真测试

3.1 测试环境

为了分析小波神经网络的数字信号调制方式识别效果, 选择常用的7种数字调制信号作为测试对象, 仿真测试平台为MATLAB2016. 实验仿真参数设置如下: 载频为150 kHz, 采样频率为1 200 kHz, 码元速率为12 500 b/s, 采样点数为10 000; 神经网络输入层节点数为6, 神经网络的隐含层节点数为13, 神经网络输出层节点数为7; 粒子群优化算法迭代次数为100, 粒子群优化算法的粒子数为20, 粒子群优化算法的权值为0.95.

3.2 结果与分析

在数字信号的信噪比分别为0和20 dB条件下, 对7种不同类型的数字信号调制方式识别, 每种信号采集的样本数量均为20, 其中15个样本数量作为训练样本集, 用于建立数字信号调制方式识别的分类器, 剩余5个样本作为测试样本集, 采用基本小波神经网络和粒子群优化算法优化小波神经网络对样本进行学习和测试, 统计数字信号调制方式识别的最优目标函数值, 得到了基本小波神经网络和粒子群优化算法优化神经网络最优解对应的目标函数值变化曲线如图3所示. 由图3可见, 无论数字信号的信噪比为0或20 dB, 粒子群优化算法优化小波神经网络的最优适应度值均优于小波神经网络, 且加快了找到最优适应度值的速度, 表明采用粒子群优化算法搜索小波神经网络的连接权值和阈值可改善小波神经网络的性能.

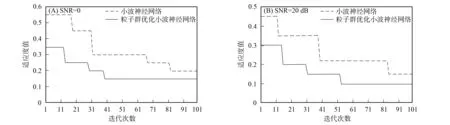
图3 不同信噪比条件下的适应度值变化曲线Fig.3 Change curves of fitness value under different signal-to-noise ratios

当数字信号的信噪比为0～ 20 dB时, 采用本文数字信号调制方式识别方法对7种信号进行分类识别, 每种数字信号调制方式识别率列于表1. 由表1可见, 数字信号的信噪比越高, 数字信号调制方式识别率越高, 表明本文对原始数字信号进行去噪可获得高质量的数字信号, 能改善数字信号调制方式识别结果, 同时对于所有数字信号调制方式, 本文方法的平均识别均达90%以上, 识别率可满足数字信号处理应用85%的要求, 说明本文的数字信号调制方式识别方法是一种有效的、 结果可靠的识别方法.

表1 不同信噪比下的数字信号调制方式识别率(%)

为表明本文提出的数字信号调制方式识别方法的优越性, 选择文献[17-18]中经典数字信号调制方式识别方法进行对比测试, 在相同的实验环境下, 数字信号的信噪比为0～ 20 dB时, 所有方法均进行10次独立的仿真实验, 统计其数字信号调制方式平均识别率和平均识别时间, 对比实验结果如图4所示.

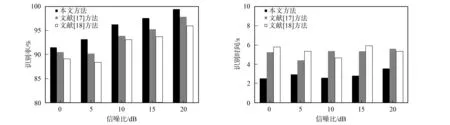
图4 与经典数字信号调制方式识别方法的性能对比Fig.4 Performance comparisons with classical methods of digital signal modulation recognition methods

由图4可见:

1) 在相同数字信号信噪比的条件下, 本文方法的数字信号调制方式平均识别率均高于文献[17]和文献[18]的数字信号调制方式识别方法, 这是由于本文算法通过小波神经网络建立了性能较优的数字信号调制方式识别分类器, 克服了当前数字信号调制方式识别方法错误率大、 对噪声鲁棒性差等缺陷, 同时通过粒子群优化算法对小波神经网络的连接权值和阈值进行在线优化, 明显减少了数字信号调制方式识别误差, 提高了数字信号调制方式识别率;

2) 在相同实验环境下, 本文方法的数字信号调制方式平均识别时间明显减少, 这是因为本文方法对原始数字信号进行了去噪处理, 抑制了噪声对数字信号调制方式建模的干扰, 提取了更优的数字信号调制方式识别特征, 简化了数字信号调制方式识别的分类器结果, 加快了数字信号调制方式识别速度, 具有更好的实用性.

综上所述, 为了提高数字信号调制方式的识别和分类性能, 本文提出了一种基于神经网络的数字信号调制方式识别方法, 首先提取数字信号的瞬时特征, 并进行归一化处理作为神经网络的输入向量; 然后通过粒子群优化神经网络构建数字信号调制方式识别的分类器; 最后通过仿真测试结果表明, 无论是数字信号的信噪比高或低, 本文方法均可获得较理想的数字信号调制方式识别结果, 具有较强的抗噪性能.

[1] Dobre O, Abid A, Bar-Ness Y, et al. Survey of Automatic Modulation Classification Techniques: Classical Approaches and New Trends [J]. IET Communieations, 2007, 21(2): 137-156.

[2] WANG Jianghong, LI Bingbing, LIU Mingqian, et al. SNR Estimation of Time-Frequency Overlapped Signals for Underlay Cognitive Radio [J]. IEEE Communications Letters, 2015, 19(11): 1925-1928.

[3] 徐闻, 王斌. 采用高阶累计量的时频混叠信号调制识别研究 [J]. 信息工程大学学报, 2013, 14(3): 299-305. (XU Wen, WANG Bin. Method of Modulation Recognition of Time-Frequency Overlapped Signals Based on High-Order Cumulants [J]. Journal of Information Engineering University, 2013, 14(3): 299-305.)

[4] 孙运全, 孙玉坤, 杨泽斌, 等. 数字信号处理技术在馈线自动化终端中的应用 [J]. 江苏大学学报(自然科学版), 2004, 25(2)： 160-163. (SUN Yunquan, SUN Yukun, YANG Zebin, et al. Application of Digital Signal Processor in Feeder-Terminal-Unit [J]. Journal of Jiangsu University (Natural Science Edition), 2004, 25(2)： 160-163.)

[5] 高建勤, 熊淑华, 赵婧. 一种基于小波的数字调制信号识别算法 [J]. 四川大学学报(自然科学版), 2007, 44(6): 1281-1284. (GAO Jianqin, XIONG Shuhua, ZHAO Jing. A Wavelet-Based Identification Algorithm of Digital Modulation Signals [J]. Journal of Sichuan University (Natural Science Edition), 2007, 44(6): 1281-1284.)

[6] 李强, 明艳, 吴坤君. 基于MATLAB的《数字信号处理》辅助教学方法 [J]. 重庆邮电大学学报(自然科学版), 2007(增刊): 89-91. (Ll Qiang, MING Yan, WU Kunjun. DS Passistant Teaching Methods Based on MATLAB [J]. Journal of Chongqing University of Posts and Telecommunications (Natural Science Edition), 2007(Suppl): 89-91.)

[7] 王兰勋, 孟祥雅, 佟婧丽. 基于循环谱和稀疏表示的多信号调制识别 [J]. 电视技术, 2015, 39(1): 92-95. (WANG Lanxun, MENG Xiangya, TONG Jingli. Multi-signals Modulation Recognition Based on Cyclic Spectrum and Sparse Representation [J]. Video Engineering, 2015, 39(1): 92-95.)

[8] 赵雄文, 郭春霞, 李景春. 基于高阶累积量和循环谱的信号调制方式混合识别算法 [J]. 电子与信息学报, 2016, 38(3): 674-680. (ZHAO Xiongwen, GUO Chunxia, LI Jingchun. Mixed Recognition Algorithm for Signal Modulation Schemes by High-Order Cumulates and Cyclic Spectrum [J]. Journal of Electronics & Information Technology, 2016, 38(3): 674-680.)

[9] 杨发权, 李赞, 罗中良. 基于聚类与神经网络的无线通信联合调制识别新方法 [J]. 中山大学学报(自然科学版), 2015, 54(2): 24-29. (YANG Faquan, LI Zan, LUO Zhongliang. A New Specific Combination Method of Wireless Communication Modulation Recognition Based on Clustering and Neural Network [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2015, 54(2): 24-29.)

[10] 龚安民, 王炳和, 曲毅. 基于同步压缩小波变换的通信信号调制识别 [J]. 电光与控制, 2015, 22(12): 50-53. (GONG Anmin, WANG Binghe, QU Yi. Modulation Recognition of Communication Signals Based on Synchro Squeezed Wavelet Transform [J]. Electronics Optics & Control, 2015, 22(12): 50-53.)

[11] Eldemerdash Y A, Dobre O A, Ner M. Signal Identification for Multiple-Antenna Wireless System: Achievements and Callendes [J]. IEEE Communications Surveys & Tutorials, 2016, 18(3): 1524-1551.

[12] 龙晓红, 张洪欣, 张明明. 基于调和平均分形盒维数的无线通信信号调制识别算法 [J]. 江苏大学学报(自然科学版), 2017, 38(3): 308-312. (LONG Xiaohong, ZHANG Hongxin, ZHANG Mingming. Recognition Algorithm of Wireless Communication Signal Modulation Based on Harmonic Mean Fractal Box Dimension [J]. Journal of Jiangsu University (Natural Science Edition), 2017, 38(3): 308-312.)

[13] 杨伟超, 杨新权. Alpha稳定分布噪声下卫星双信号调制识别 [J]. 应用科学学报, 2017, 35(3): 309-316. (YANG Weichao, YANG Xinquan. Modulation Recognition of Double Satellite Signals in Alpha-Stable Distribution Noise [J]. Journal of Applied Sciences-Electronics and Information Engineering, 2017, 35(3): 309-316.)

[14] 张洋, 彭华. 单通道混合信号调制识别 [J]. 信息工程大学学报, 2016, 17(6): 662-668. (ZHANG Yang, PENG Hua. Modulation Recognition for Mixed Signals in Single Channel [J]. Journal of Information Engineering University, 2016, 17(6): 662-668.)

[15] 赵自璐, 王世练, 张炜, 等. 水下冲激噪声环境下基于多特征融合的信号调制方式识别 [J]. 厦门大学学报(自然科学版), 2017, 56(3): 416-422. (ZHAO Zilu, WANG Shilian, ZHANG Wei, et al. Classification of Signal Modulation Types Based on Multi-features Fusion in Impulse Noise Underwater [J]. Journal of Xiamen University (Natural Science), 2017, 56(3): 416-422.)

[16] 刘涛, 孟青, 韩建宁. 基于神经网络的计算机通信系统干扰信号分离 [J]. 吉林大学学报(理学版), 2017, 55(6): 1545-1551. (LIU Tao, MENG Qing, HAN Jianning. Interference Signal Separation of Computer Communication System Based on Neural Network [J]. Journal of Jilin University (Science Edition), 2017, 55(6): 1545-1551.)

[17] 赵雄文, 郭春霞, 李景春. 基于高阶累积量和循环谱的信号调制方式混合识别算法 [J]. 电子与信息学报, 2016, 38(3): 674-680. (ZHAO Xiongwen, GUO Chunxia, LI Jingchun. Mixed Recognition Algorithm for Signal Modulation Schemes by High-Order Cumulants and Cyclic Spectrum [J]. Journal of Electronics & Information Technology, 2016, 38(3): 674-680.)

[18] 赵宇峰, 曹玉健, 纪勇, 等. 基于循环频率特征的单信道混合通信信号的调制识别 [J]. 电子与信息学报, 2014, 36(5): 1202-1208. (ZHAO Yufeng, CAO Yujian, JI Yong, et al. Modulation Identification for Single-Channel Mixed Communication Signals Based on Cyclic Frequency Features [J]. Journal of Electronics & Information Technology, 2014, 36(5): 1202-1208.)