一种惯性权重与种群多样性协同调整的二进制粒子群优化算法
2018-03-27李浩君王万良
李浩君,张 广,王万良
1(浙江工业大学 教育科学与技术学院,杭州 310023) 2(浙江工业大学 计算机科学与技术学院,杭州 310023)
1 引 言
粒子群算法(Particle Optical Swarm)是由美国心理学家Kennedy和电气工程师Eberhart[1]在1995年提出的一种演化计算技术,广泛应用于电力、化工、经济等工程领域的优化问题[2-4].由于实际当中很多问题并非是连续性的问题而是离散性的问题,Kennedy[5]又提出一种二进制粒子群算法,用来解决工程领域离散性的优化组合问题.不论是标准粒子群算法还是二进制粒子群算法,都是根据种群之间的信息来判断搜索最优值,所以种群多样性和搜索能力往往决定着粒子群算法的效率和准确度.但标准粒子群算法惯性权重值不能动态改变进而调整粒子群算法的搜索范围,并随着种群多样性的下降,易过早陷入局部收敛,不能获取最优值.针对粒子群算法的缺点,很多学者都提出了改进策略,首先Shi等学者[6,7]根据粒子群算法的迭代次数与多样性之间的线性关系,动态改变标准粒子群的惯性权重值,权重值随着迭代次数增加不断下降,从而在算法前期以较大权重值提高粒子群算法全局搜索能力,在算法后期以较小权重值增加局部探索能力,但只根据粒子群与权重之间简单的线性关系,还无法根据种群多样性精确地调节权值.Riget等学者[8-10]提出基于粒子之间的欧氏距离判断种群多样性,动态调节算法的权重,但是又往往忽略的权重值与迭代次数之间的线性关系.目前有关二进制粒子群算法的种群多样性与惯性权重相互影响的关系研究还比较少.部分学者[11-13]还引入混沌理论对粒子群的种群多样性进行改进,但是缺少使用混沌理论对二进制粒子群算法的种群多样性进行动态调整的研究.
本文提出一种基于种群多样性与惯性权重协同调整的粒子群优化算法Coordinated Adjustment Binary Practical Swarm Optimization(CBPSO),根据二进制粒子群的海明距离均值和迭代次数变化动态调整权重值,再根据海明距离使用混沌理论动态调整种群多样性,最后根据种群多样性的变化在新的迭代中重新调整惯性权重值,从而改进种群无法有效探索以及随着迭代次数增加种群多样性过快下降的缺点,进而提高二进制粒子群算法的效率,实验证明,该算法具有较好的准确性与鲁棒性.
2 二进制粒子群算法优化的基本原理
粒子群算法以模拟鸟的群体智能为特征,每只鸟被称之为一个粒子.粒子群优化算法首先初始化包含一群随机的d维粒子的种群,每个粒子的每一维都由其速度和位置两方面向量信息进行表示,第i个粒子的速度和位置表示如下:Vi=[vi1,vi2,…,vij],Xi=[xi1,xi2,…,xij].算法采用一个适应度函数来评价粒子当前位置的优劣,通过不断迭代,最终找到最优解或近似最优解.在每次迭代中,粒子通过跟踪个体最优解和群体最优解来更新自己的速度和位置.更新公式如下:
(1)
(2)
k迭代次数;c1、c2为学习因子;r1、r2是分布在[0,1]内的随机数;pij为粒子本身找到的个体最优解;gij为整个粒子群中当前找到的群体最优解.
基本粒子群算法是针对连续域的问题设计的,但许多优化问题是针对离散的,因此文献[5]对此进行了扩展,提出一种离散二进制BPSO算法,在二进制粒子群算法中,粒子运动的轨迹和速度是从概率角度定义的,每个粒子的每一位xi的取值为0或取1的概率 其基本公式如下:

(3)
S函数一般用Sigmoid函数表示,二进制粒子群算法的其他部分同基本粒子群算法.
3 协同调整的二进制粒子群优化算法
3.1 算法基本思想
粒子群算法运行时,在保持惯性权重不断下降和粒子群逐渐收敛的趋势下,当种群多样性较差陷入局部最优时,需要对种群进行发散操作增加多样性,惯性权重值也应该相应的增大,使粒子群在更大范围内进行探索,从而能够跳出局部最优;当种群多样性较好,则通过海明距离均值和当前迭代状态共同动态调整惯性权重值,从而平衡全局搜索和局部开发能力,使之逐步收敛至全局最优值.
本文采用这一研究思路对惯性权重和种群多样性进行协同调整,提出根据每个粒子与最优粒子的海明距离均值与当前迭代状态,动态协同调整粒子群惯性权重和多样性的粒子群优化算法.首先使用混沌函数初始化种群;其次把海明距离均值与之前学者提出的惯性权重递减方法结合,在保持惯性权重整体下降的前提下,根据海明距离均值变化更加有针对性的对惯性权重进行动态增减,从而更好平衡粒子群的全局搜索能力与局部开发能力;再次根据每个粒子和最优粒子的海明距离均值对种群多样性进行动态调整,改善种群多样性,防止过早收敛陷入局部最优,同时又不过度干扰粒子群算法不断收敛的趋势.最后根据种群多样性的变化,在新的迭次过程中,对惯性权重值进行相应的调整.
3.1.1 混沌初始化
为了保持种群多样性与遍历性,用Logistic映射产生混沌序列X.
Xn+1=μXn(1-Xn)
(4)
X0=r and(0,1),μ=4且Xn≠0.25,0.75,0.5;如果Xn大于0.5,Xn等于1,反之等于0.
3.1.2 二进制粒子群多样性和距离度量方法
为了表示两个粒子之间的距离,引入了海明距离,定义粒子含有决策变量的个数即为粒子的维数,如Xij,其下标 i 表示群体中的第 i 个粒子,j 表示该粒子的第j个决策变量.若粒子的每一维决策变量用m个二进制位编码表示,任意两个粒子X1和X2的距离可由海明距离表示为:|X1-X2|=D(X1,X2).其中D是计算海明距离的函数,其值为两个二进制位串中不同位的个数.为了降低计算的复杂度,计算每个粒子与全局最优粒子之间的海明距离均值来判断种群的多样性,并不是计算所有粒子之间的海明距离均值.
3.1.3 权重协同调整
通过海明距离均值、惯性权重与迭代次数之间的线性关系共同调节惯性权重,公式(5)的前半部分((1-e-HD/k)*a)为通过海明距离均值的权重调节公式,公式(5)后半部分((1- t/T )(Wmax-Wwin)+Wwin)为通过迭代次数调整的调节公式.
W=((1-e-HD/k)*a)*((1-t/T)*(Wmax-Wwin)+Wwin)
(5)
其中HD为当前粒子与最优值粒子之间的海明距离均值,其值随着多样性变化动态改变.T为粒子群算法的最大迭代次数,t当前迭代次数,Wmax和Wwin为权重最大值和最小值,k用来调节指数函数对HD变化的敏感度,a用来调整公式(5)前半部分和后半部分共同变化的速率.
公式(5)惯性权重随着海明距离均值和迭代次数共同变化,在搜索初期惯性权重W较大,使粒子群在可以在全局范围内进行探索;在搜索中后期,随着海明距离均值与迭代次数动态调整,有利于平衡粒子群全局探索和局部开发能力.
3.1.4 种群多样性自适应调整
计算每个粒子与全局最优粒子之间的海明距离均值HD,然后设定阈值D的变化区间.如果HD小于阈值,对种群多样性进行发散调整,同时阈值动态减小.由于二进制粒子群算法的随机性,其他算法如加速度调节算法、权重自适应调整[14,15],对参数的变化区间都是根据大量实验观察设定.本文根据大量实验观察设定阈值D的范围.
3.2 算法步骤
步骤1.混沌初始化
对所有粒子用公式(4)混沌初始化位置.
步骤2.初始化种群参数
初始化粒子群的个体学习因子和社会学习因子值、迭代次数、Fitness数值精度、加速度值为位于区间(0,1)随机值,初始权重值设为1.
步骤3.初始化阈值
设定阈值下限为粒子维度的1/7,上限为粒子维度的4/7.
步骤4.计算初始化适应度值
根据初始化的粒子位置与速度,带入适应度函数,求出适应度值.如能满足要求则终止,不能满足要求则继续执行.
步骤5.计算海明距离均值并排序
计算每个粒子与全局最优粒子之间的海明距离均值,并按与最优粒子之间的海明距离对粒子群从小到大排序.
步骤6.惯性权重协同调整
按公式(5)计算惯性权重的值,并且判断惯性权重w的值是否在范围Wmax和Wwin之间,如果大于Wmax,则值为如果小于Wwin,则值为Wwin,根据惯性权重调整策略对权重进行动态调整.
步骤7.粒子位置速度更新策略
速度更新公式:
(6)
位置更新公式:

(7)

步骤8.种群多样性自适应调整
如果海明距离均值HD小于动态阈值,对种群按海明距离由小到大排序,取前50%种群再次进行混沌化处理,如果海明距离均值HD大于阈值下限,D减去1.
步骤9.终止条件判断
判断算法是否达到最大迭代次数或者适应度值满足要求,如果满足就转步骤十.否则就转步骤五,并重新计算海明距离均值,并根据海明距离均值重新计算新的惯性权重值;
步骤10.输出数据
输出全局最优解,并求出相应的目标函数值,算法结束.
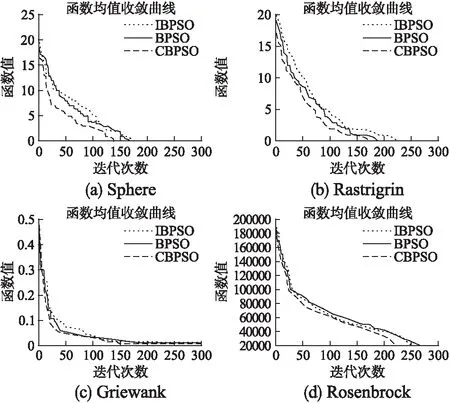
图1 函数均值收敛曲线Fig.1 Convergence curve of function mean

表1 算法在Sphere函数上实验结果Table 1 Algorithm results on the Sphere function
表2 算法在Rosenbrock函数上实验结果
Table 2 Algorithm results on the Rosenbrock function

F4D=30,M=10,Imax=100D=50,M=30,Imax=300D=100,M=50,Imax=10000均值方差成功率耗时/s均值方差成功率耗时/s均值方差成功率耗时/sCBPSOBPSOIBPSO760088009700268E+05308E+05368E+050.370.280.253.02.62.6414004600052300134E+06160E+06196E+060.050.020.019.19.59.776E+0499E+0495E+04706E+05886E+05871E+050.030.010.00656679690
表3 算法在Rastrigrin函数上实验结果
Table 3 Algorithm results on the Rastrigrin function

F2D=30,M=10,Imax=100D=50,M=30,Imax=300D=100,M=50,Imax=10000均值方差成功率耗时/s均值方差成功率耗时/s均值方差成功率耗时/sCBPSOBPSOIBPSO0.070.130.10605E⁃04983E⁃04810E⁃040.930.870.902.72.32.30.080.150.14677E⁃041083E⁃041035E⁃040.900.850.867.27.57.50.991.081.03204E⁃04110E⁃03518E⁃040.060.010.02635650652
表4 算法在Griewank函数上实验结果
Table 4 Algorithm results on the Griewank function

F3D=30,M=10,Imax=100D=50,M=30,Imax=300D=100,M=50,Imax=10000均值方差成功率耗时/s均值方差成功率耗时/s均值方差成功率耗时/sCBPSOBPSOIBPSO0.00130.00190.0022263E⁃07198E⁃07335E⁃070.920.860.842.82.52.60.0070.0100.009354E⁃07867E⁃07565E⁃070.880.830.807.37.57.90.00010.00030.0002102E⁃08203E⁃08201E⁃080.050.010.01665671686
4 试验及分析
4.1 实验设置
二进制粒子群算法常用的实验方法有基于Benchmark函数和背包问题两种测试方法,本文选用基准函数进行测试,基本粒子群算法粒子初始值为实数,不同于基本粒子群算法,二进制粒子群算法初始粒子初始值为二进制值.选用广泛使用的Sphere、Rastrigrin、Griewank、Rosenbrock函数对算法进行测试,其中Sphere、Rosenbrock为单峰函数,其它两个函数为复杂的多峰函数.具体函数参数如表5所示.
表5 测试函数
Table 5 Test functions

函数名称表达式极值SphereF1=∑Di=1x2i0RastrigrinF2=∑Di=1[x2i-10cos(2πxi)+10]0GriewankF3=1/400∑Di=1x2i-∏Di=1cosxii+10RosenbrockF4=∑Di=1(1-xi)2+100(xi+1-x2)20
算法的参数设置如下:Wmax=1.5,Wmin=0.5.Dmax=n/7,Dmax=4n/7,a=2,k=4.表1至表4中,D代表维度,M代表种群数量,Imax代表迭代次数.本文引入Shi和Eberhart提出的惯性权重改进算法[6]进行对比,文中命名此算法为IBPSO.
本次实验采用以下评价标准判断三种算法的效率,评价标准如下:
1)最优值:算法迭代t次收敛后,适应度函数的最小值即最优值.
2)均值:算法执行n次后,n个最优值的均值.
3)方差:算法执行n次后,n个最优值的方差.
4)成功率:算法收敛至全局最优解次数与实验次数的比值,再乘以100%.
5)耗时:算法执行n次后,收敛至全局最优解时,执行时间的均值.
算法仿真实验环境为Windows10操作系统,编程语言环境Python3.3.硬件环境为intel酷睿处理器i5-2250,主频为 2.50GHz,内存为4GB.
4.2 实验结果及分析
表1-表4分别为四个基准函数在维度为30、50、100,不同迭代次数条件下,算法执行50次的均值、方差、耗时和成功率.对于复杂度不高的单峰函数Sphere,三种算法在不同维度下均能取得了较好的成功率,其中CBPSO算法成功率最高,均值和方差最小,BPSO和IBPSO算法相近,IBPSO算法效果稍好于BPSO算法,但效率提升并不大.
对于较难寻优的复杂函数及多峰函数,F3,F4,由表2至表4可以看出CBPSO算法均值最小,寻优成功率高.原因是CBPSO算法根据种海明距离均值和迭代次数两种因素协同调整惯性权重,在迭代初期能以较大的惯性权重进行全局搜索,在迭代中后期惯性权重值能根据种群多样性变化更加精准调整,且不会下降过早造成全局搜索能力过早下降.而IBPSO算法的寻优成功率不如BPSO,原因是IBPSO在迭代次数较少的情况下,如果权重值设置较小,权重值会根据迭代次数下降过快,在算法需要在全局搜索最优值的时候,不能在全局进行探索.
由于文中对Rosenbrock函数采用二进制方式编码进行优化,适应度值呈阶梯状下降,所以均值和方差数值较大.
图1为三种算法在维度为50的情况下,平均适应度值的收敛曲线.可以看出在相同的参数下,IBPSO算法收敛的平均代数最少,平均收敛值最小.由于迭代过程中通过对种群多样性和惯性权重值的动态调整,单峰函数函数通过CBPSO算法寻优的过程中,适应度值变化较快,在提高收敛精度的情况下,寻优成功率也提高.对于其他函数,由于极值点分布在多峰的谷底,难以寻优,而CBPSO算法通过对多样性调整,重新增加了种群多样性,增大了惯性权重值,使算法可以跳出局部最优,重新探索全局最优值;在粒子群不断收敛在局部寻找最优值时,惯性权重可以动态增减,使函数在谷底进行更好的局部探索.改变了IBPSO算法惯性权重下降过快、不够准确的缺点.能更加精确根据对惯性权重和粒子群多样性进行变化控制.
对比CBPSO、BPSO和IBPSO算法在种群数量为30,50,100时算法收敛时执行时间,对算法执行50次,得到算法收敛至全局最优解的平均执行时间,如表2所示:CBPSO算法执行时间开始略高于IBPSO、BPSO算法,原因是CBPSO 算法增加了种群多样性,一定程度干扰了粒子群不断收敛的趋势,对于海明距离均值的计算增加了算法时间复杂度.但随着资源数量增加带来问题复杂度的增长,CBPSO算法对种群多样性和惯性权重进行动态协同调整,从而使收敛更为准确的优势展现出来,尤其在其他两种算法陷入局部最优难以逃离的时,CBPSO算法更为快速的收敛至最优值,CBPSO算法在准确率提高的情况下,收敛至全局最优解的平均执行时间也逐步优于其他算法.
5 结束语
本文提出的CBPSO算法,利用海明距离均值提升粒子群的探索能力,实现了协同调整惯性权重值和粒子群种群多样性的目标.实验表明,本文提出的算法具有较高的精准度和较好的鲁棒性,CBPSO算法在迭代过程中具有较好的跳出和探索能力,从而能在一定程度上提高种群多样性与探索能力,提高搜索的准确度,获得精确的适应度值.但本文的多样性调整策略,在执行过程中存在调整次数过多导致时间复杂度较高的问题,在权重调整中,函数对海明距离变化敏感度不够灵敏的问题,需要在以后工作中持续研究改进.
[1] Kennedy J,Eberhart R.Particle swarm optimization [C].IEEE International Conference on Neural Networks,Perth,Australia,Proceedings,IEEE,1995:1942-1948.
[2] Bharti K K,Singh P K.Opposition chaotic fitness mutation based adaptive inertia weight BPSO for feature selection in text clustering[J].Applied Soft Computing,2016,43(6):20-34.
[3] Li Tao-shen,Chen Song-qiao,Yang Ming,et al.Application of an improved particle swarm optimization algorithm in QoS anycast routing[J].Journal of Chinese Computer Systems,2010,31(1):67-71.
[4] Wu Yan-wen,Wang Jie,Wang Fei.Collaborative filtering recommendation model based on hybrid particle swarm optimization and genetic algorithm[J].Journal of Chinese Computer Systems,2017,38(3):527-530.
[5] Kennedy J,Eberhart R.A discrete binary version of the particle swarm algorithm[C].IEEE International Conference on Systems,Man,and Cybernetics,Computational Cybernetics and Simulation,IEEE,1997,5:4104-4108.
[6] Shi Y,Eberhart R.A modified particle swarm optimizer[C].IEEE International Conference on Evolutionary Computation Proceedings,IEEE World Congress on Computational Intelligence,IEEE,1998:69-73.
[7] Shi Y,Eberhart R C.Empirical study of particle swarm optimization[J].Frontiers of Computer Science in China,1999,3(1):31-37.
[8] Riget J,Vesterstrøm J S.A diversity-guided particle swarm optimizer-the ARPSO[J].Dept.Comput.Sci,Univ.of Aarhus,Aarhus,Denmark,Tech.Rep,2002,2:2002.
[9] Ursem R K.Diversity-guided evolutionary algorithms [C].International Conference on Parallel Problem Solving from Nature.Springer Berlin Heidelberg,2002:462-471.
[10] Ren Zi-hui,Wang Jian.An adaptive particle swarm optimization algorithm for dynamic change of inertia weight[J].Computer Science,2009,36(2):227-229.
[11] Cui X,Jiang M.Chaotic time series prediction based pn binary particle swarm optimization [J].Aasri Procedia,2012,1(3):377-383.
[12] Zhang T,Cai J D.A new chaotic PSO with dynamic inertia weight for economic dispatch problem[C].International Conference on Sustainable Power Generation and Supply,Supergen,IEEE,2009:1-6.
[13] Song Y,Chen Z,Yuan Z.New chaotic PSO-based neural network predictive control for nonlinear process[J].IEEE Transactions on Neural Networks,2007,18(2):595-600.
[14] Chih M.Self-adaptive check and repair operator based particle swarm optimization for the multidimensional knapsack problem [J].Applied Soft Computing,2015,26(1):378-389.
[15] Polprasert J,Ongsakul W,Dieu V N.Self-organizing hierarchical particle swarm optimization with time-varying acceleration coefficients for economic dispatch with valve point effects and multifuel options[C].Proceedings of the Fourth Global Conference on Power Control and Optimization,American Institute of Physics,2011:85-92.
附中文参考文献:
[3] 李陶深,陈松乔,杨 明,等.改进的粒子群优化算法在QoS选播路由中的应用[J].小型微型计算机系统,2010,31(1):67-71.
[4] 吴彦文,王 洁,王 飞.混合粒子群遗传算法的协同过滤推荐模型[J].小型微型计算机系统,2017,38(3):527-530.
[10] 任子晖,王 坚.一种动态改变惯性权重的自适应粒子群算法[J].计算机科学,2009,36(2):227-229.
