基于GHM多小波的股票收益率的多尺度分析

周小辉,黄 翠

1.浙江财经大学东方学院，嘉兴，314408;2.上海财经大学数学学院，杨浦，200433

1 引 言

股票交易是证券市场中最活跃的资本运作行为之一，其参与者是各式各样的群体，包括日内交易者、投资组合经理、商业银行、大型公司和中央银行等。这些参与者的操作时间尺度大不相同。由于交易者之间不同的决策时间尺度，股票收益率的真实动态分析也随着不同投资期的时间尺度而变化。因此，低频与高频的震荡将以不同的方式影响市场。所以，需要一种计量经济的方法在不同的时间尺度去获取基本的动态结构，这涉及从整体动态到局部动态的分离，例如长期变化中的短暂变化。由于通常采用的仅仅是两个时间尺度(长期与短期)，因此对于这项工作，传统的方法能力有限。而小波分析的一个独有的特征是能够处理非平稳数据，在时域中局部化，且根据所需的时间尺度对信号进行多尺度分析，小波协方差可以分解在不同时间尺度上两个随机过程间的方差。在一个特定尺度上的小波协方差反映了对随机变量间协方差的贡献度。小波分析的这种特征可以用来研究不同时间尺度上的协方差/相关系数。因此，近年来，一些学者尝试用小波分析来分析经济与金融中的相关问题。例如，龙会典基于小波滤波器研究了一种关于进出口量的复合预测算法[1]； Gallegati在专著《Wavelet Applications in Economics and Finance》中提供了一些利用小波理论在经济与金融相关问题中进行应用研究的方法概述与应用范例[2]；王健基于极大重叠离散小波变换研究了中美股市的联动性[3]；张林利用小波分析的方法研究金融危机时点的探测[4]；刘向丽采用小波分析的方法研究了一种股指期货高频预测的方法等[5]。可见，小波分析在经济与金融中的应用已经成为一个重要的研究方向。

综上所述，本文拟采用多小波算法来研究经济与金融相关问题。文中选择的滤波器是GHM多小波滤波器、多小波分解重构算法进行某只股票的多尺度分析。

2 基本原理与公式

多小波理论是建立在r重多分辨分析前提下的。基于r重多分辨分析理论,可以推导出多小波的分解与重构算法。任意一连续信号f(x)∈Vj+1，则分解算法为

(1)

(2)

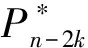
利用多小波变换得到小波系数时，这些小波系数反映了某个给定尺度下的变化情况同时也可以得到该尺度下小波高频的方差。换句话说，小波高频的方差的基本思想是用某些尺度上变化的概念来取代用样本方差估计变化的整体度量。对于长度为二进制数N=2J的时间序列X的小波高频的方差，可以利用尺度λj=2j-1的小波系数来估计，表达式如下：

(3)

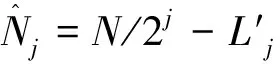
在统计意义上，计算小波相关系数是必要的。小波高频的相关系数可以利用{Xt,Yt}的小波协方差与Xt和Yt的小波方差来简单构造。在尺度为λj时小波相关系数可表示如下：

(4)

3 数据的选取与描述性统计

根据研究的需要，选取2015年11月11日—2017年12月13日期间股票宝信软件的每日收盘股价(单位：元)。除去周末与节假日，每年有246个交易日，即每年有246个数据点。在研究期限中，一共产生了512个每日数据点，且数据源于同花顺。根据描述性统计可知，在2015年11月11日—2017年12月13日期间，宝信软件每日股价的最大值为70.72元，最小值为14.57元，方差为191.937 6，如表1所示。

表1 基本的统计

注：此表给出了2015年11月11日—2017年12月13日期间宝信软件每日股价及其每日收益率的均值、方差、最值、峰度以及偏度等信息。偏度和峰度分别定义为E(Xt-μ)3与E(Xt-μ)4，其中μ是样本均值。

该期间宝信软件每日股价与每日收益率的变化见图1。

图1 宝信软件股价与日收益率

由图1可知，股价在2015年11月11日为最大值70.72元，随后不断波动缓慢下跌，两个月之后呈现明显下跌趋势，在2016年5月9日(第121个样本点)每10股转赠10股，当日收盘股价变为21.24元。之后小幅下调一个多月后股票价格又开始回升至最高25.2元，之后持续波动缓慢下跌至2017年6月2日达到最小值14.57元，至2017年12月13日持续振荡。在2015年11月11日至2017年12月13日期间，宝信软件股价的日收益率变化中，每日收益率是通过lnXt+1-lnXt计算所得。

4 多尺度实证分析

采用多小波变换对2015年11月11日—2017年12月13日期间宝信软件及其每日收益率进行多尺度实证分析。为了研究多小波算法在上证指数及其收益率的应用，选择长度为3的GHM多小波滤波器。

首先利用多小波分解算法对2015年11月11日—2017年12月13日期间宝信软件的每日收益率进行多小波分解，以研究对数收益率的多尺度变化，分解原始每日收益率至第6层(第6尺度)。注意越低的尺度对应越高的频率带。如图2所示，高频d1反映了2015年11月11日—2017年12月13日期间宝信软件的日收益率2-4天的波动变化(第1层)，而高频d2给出了4-8天的振荡情况(第2层)，高频d3给出了8-16天的变化情况(第3层)。第一层高频d1的波动振荡比较剧烈；d2和d3这两层的波动相对较小；相比16-32天(dd4,第4层)、32-64天(d5,第5层)以及64-128天(d6,第6层)的波动，它们的波动曲线比较光滑，且总体上振幅减小，尤其是d5与d6，其中d4和d6周期性振荡频繁，而d5振荡较弱。这说明随着尺度的增加，高频波动的大小不断递减；即随着考察时间期限的增加，相应收益率的波动不断减小。该结果符合客观事实，说明短期投资的投资者必须在实际收益的每一次振荡中做出必要的反应，同时作为长期投资者而言，则没有这么显著。另外，在高频d2与d3中非常直观地发现在第121个样本点附近日收益率存在较大的振荡，这是多小波高频检测出的日收益率突变点。它反映了额外的信息，即在2016年5月9日(第121个样本点)每10股转赠10股，当日收盘股价变为21.24元。这说明多小波方法可以检测金融数据(如股价)的突变点。

图2 宝信软件日收益率的多尺度分析

另一方面，通过小波方差估计也可以说明上述结论。根据(3)式，计算每日对数收益率高频d1的方差估计为0.749 6×10-3，d2的方差估计为0.412 8×10-3，d3的方差估计为0.329 2×10-3，d4的方差估计为0.074 3×10-3，d5的方差估计为0.133 1×10-3，d6的方差估计为0.011 0×10-3。图3给出了方差估计随着尺度增加的变化。小波方差都是随着尺度增加而递减的，从d1到d4呈现近似线性的递减关系，从d4到d5稍微有所回升，而d5到d6呈现递减关系。这一现象(方差随着尺度增加而减少)一方面说明了短期投资收益波动较大，对于投资者必须在实际收益的每一次振荡中做出必要的反应。另一方面，说明了利用多小波对上证指数的每日收益率进行多尺度分解时层数不必太多，这一点对于减少计算量、提高数据处理速度有益。

图3 小波方差估计图

进一步利用Matlab计算了多小波高频指数d1，d2，d3，d4，d5和d6之间的相关系数如表2。

表2 不同尺度下多小波高频指数间的相关系数

注：表中给出了多小波高频指数d1，d2，d3，d4，d5和d6之间的相关性系数。

从表2可知，高频指数d1和d3相关系数最大，其值为0.006 9，d2和d6相关系数最小，其值为0.000 0，其他高频指数之间的相关系数有正有负，且绝对值都小于0.07，反映了多小波高频指数之间的相关性程度较弱。此结论说明了2015年11月11日—2017年12月13日期间宝信软件的对数收益率波动情况中，2-4天与8-16天的波动变化相关性是最大的，相比其他的期限而言，4-8天与64-128天的波动变化相关性最小。同时，各时间天度之间波动相关性的程度也是较弱的。进而，这种结论表明在不同时间尺度下波动变化的相关性都较弱。所以，投资者可以根据实际情况，在不同时间尺度下分析投资策略与对冲风险。

5 结 论

本文以2015年11月11日—2017年12月13日期间股票宝信软件的每日股价为例，基于GHM多小波滤波器进行股票收益率的多尺度分析，主要包括以下结论：(1)随着尺度的增加，高频波动的大小不断递减；即随着考察时间期限的增加，相应收益率的波动不断减小。该结果符合客观事实，说明短期投资的投资者必须在实际收益的每一次振荡中做出必要的反应，同时作为长期投资者而言，没有这么显著；(2)多小波高频指数的方差随着尺度增加以递减的速度减少，之后趋向于平稳。这一现象一方面说明了短期投资收益波动较大，对于投资者必须在实际收益的每一次振荡中做出必要的反应。另一方面，说明了利用多小波对上证指数的每日收益率进行多尺度分解时层数不必太多，这一点对于减少计算量、提高数据处理速度有益；(3)在不同时间尺度下波动变化的相关性都非常微弱。所以，投资者可以根据实际情况，在不同时间尺度下分析投资策略与对冲风险。