基于ARIMA模型的安徽居民消费价格指数实证分析
2018-03-26杨晓伟刘相国陶有田
杨晓伟 刘相国 陶有田
(巢湖学院,安徽 巢湖 238000)
1 引言
大数据时代的到来产生了海量数据,为了有效地从数据中提取有用信息,也为了更好地对数据进行分析与预测,出现了许多具有重要实际意义的相关指数。长期以来,与人们生活息息相关的居民消费价格指数(CPI)备受关注。CPI是用来评价某段时间内人们购置物品(或进行消费服务)产生的物价波动趋势的宏观经济指标[1],其不仅是宏观经济分析与预测的重要评价指标,也是国内生产总值核算的主要量化测算指标[2]。准确的分析和预测CPI不仅是计量经济学长期研讨的热点问题,也是政府有关部门合理制定宏观经济政策的重要参考依据[3]。
时间序列分析是一种能够应用于实际社会生活的定量分析或者预测的统计方法,该方法多数运用于刻画和探究事物随时间推移而发生改变的量化型统计规律性[4]。平稳时间序列(ARMA)模型与非平稳时间序列(ARIMA)模型是目前分析时间序列的主要模型[5]。国内已经有许多专家和学者构建了大量的时间序列分析模型并对其相关领域进行了深入的研究,为宏观经济预测与决策提供了理论技术指导。本文依据安徽省2010年1月至2018年8月的实际CPI数据①安徽省统计局网站:http://www.ahtjj.gov.cn/tjjweb/web/index.jsp.,构建了基于ARIMA的CPI统计预测模型[6]。
2 时间序列分析模型
2.1 平稳时间序列模型
针对平稳时间序列,若利用其均值与方差均为常值的特性来识别某预处理后的平稳序列,则该序列会表现出在某个常值周围随机波动,且具有有限的波动范围[7]。一般判别某序列是非平稳的,通过观察该序列时序图的变化趋势,可以发现其具有显著的周期性特征。如果某平稳序列包含更多其他信息,则该序列会被检测为非白噪声的。在统计研究分析中,为了能够高效地提取序列的有用信息,考虑借助线性模型对此序列的波动情况进行拟合与逼近。目前,应用ARMA模型对平稳时间序列进行分析与预测是普遍认可的。
自回归移动平均模型简称ARMA模型,而AR模型、MA模型和ARMA模型是它的三种细化的结构模型分类[8]。
AR(q)模型全称p阶自回归模型,且满足如下结构模型:

MA(q)模型全称q阶移动平均模型,且满足如下结构模型:

ARMA(p,q)模型全称自回归移动平均模型,且满足如下结构模型:

针对ARMA(p,q)模型,我们如果引进相应的延迟算子,则有

代表ARMA(p,q)模型的p阶自回归系数多项式;
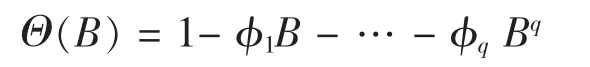
代表ARMA(p,q)模型的q阶移动平均系数多项式。
当p=0或者q=0时,显然有
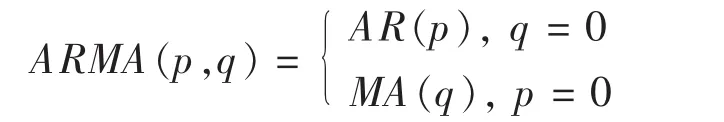
2.2 非平稳时间序列分析模型
非平稳的时间序列在实际生活中是经常出现的,并对社会生产具有显著影响,因此,研究非平稳时间序列对现实社会生产具有重要的实践指导意义。如果对非平稳序列进行差分运算后显示出平稳性的时间序列,称之为差分平稳时间序列[9]。针对差分平稳时间序列,目前分析与预测的模型主要是ARIMA模型[10]。
ARIMA(p,d,q) 模型的结构如下:

式中:▽d=(1-B)d;{εt}是一个白噪声序列且E(εt)=0;Φ(B)=1-φ1B-…-φpBp、Θ(B)=1-φ1B-… -φqBq与平稳可逆ARMA(p,q)模型中关于系数多项式的定义是一致的。
特别地,当 d=1,p=q=0 时,ARIMA(0,1,0)模型将简化为xt=xt-1=εt,此时,称该模型为随机游走模型或者醉汉模型。
3 基于ARIMA的居民消费价格指数模型
居民消费价格指数是目前国际社会广泛编制认可的一种宏观经济指标,它能够较为准确地反映市场经济的动态变化趋势,为政府有关部门确定薪资标准以及调控物价水平提供重要依据[11]。宏观经济政策有效制定的前提条件之一就是需要准确的量化分析与预测物价水平。下面针对2010年1月至2018年8月安徽省实际CPI数据进行分析并预测安徽省2018年9月至11月的CPI。
3.1 数据的预处理与分析
本文数据来源于安徽省统计局,将实际数据导入EXCEL表格整理得到样本数据,并利用SPSS软件做出CPI的时间序列图,如图1所示。
从图1可以看出,安徽省CPI的数据具有长期变化趋势,因此该序列是非平稳的时间序列。对原序列做一阶差分预处理▽xt=xt-xt-1,这样可以达到消除原序列的变化趋势以及降低其波动范围的目的。图2是对原序列进行一阶差分运算后的时序图。

图1 安徽省CPI原时间序列图
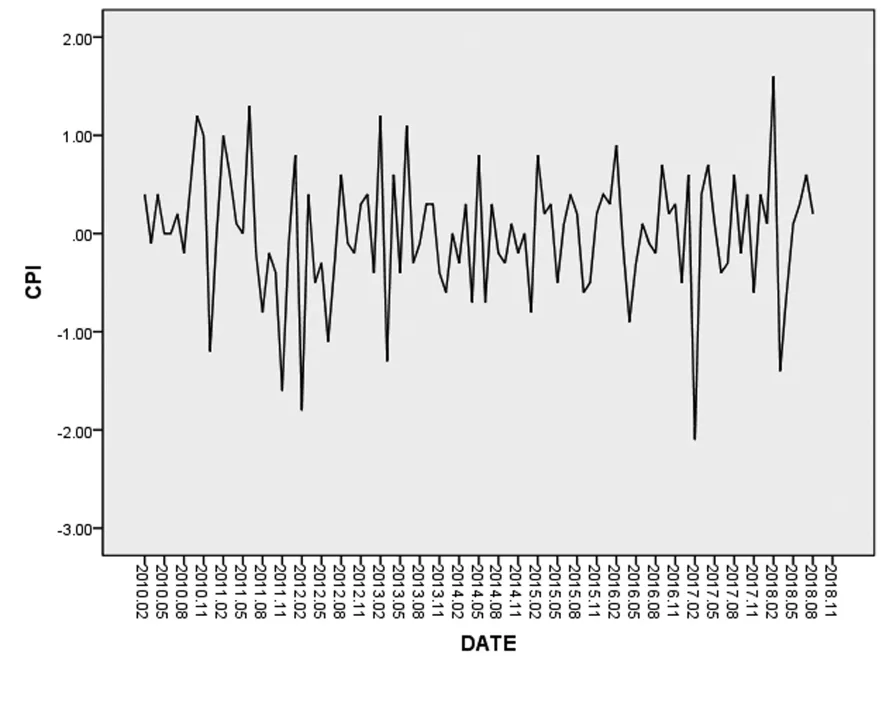
图2 安徽省CPI一阶差分后的时间序列图
由图2可看出,经过差分预处理后,基本消除了原序列的变化趋势,可以判断该序列满足了时间序列的平稳性。
为了更有效、准确地识别序列的平稳性,我们分别做了原CPI序列和一阶差分后的CPI时间序列自相关系数表格(表1和表2),并进行了对比。
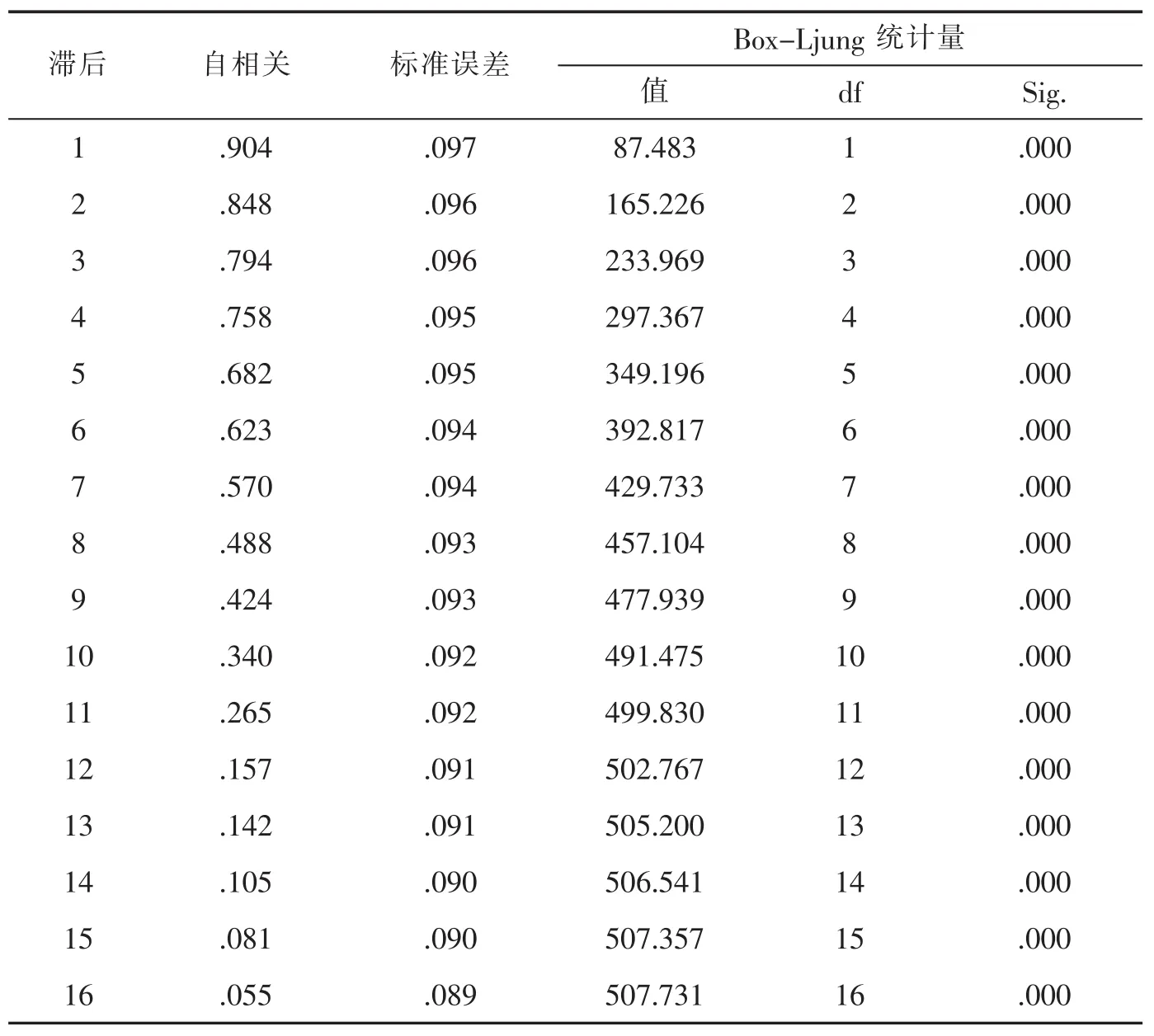
表1 原时间序列的自相关系数

表2 一阶差分后的自相关系数
表1和表2输出的结果显示原序列的自相关系数是缓慢变小的,但差分运算后的序列其自相关系数在较短延迟时期里快速向0趋近,其数值都比较小,且都在0值附近以一个很小的幅度随机波动。结合上述样本的时序图、自相关系数表格和平稳时间序列的性质,可以判定原序列是非平稳的,而经过差分处理后的序列是平稳的并且是白噪声的。
3.2 基于ARIMA的物价指数模型的分析与预测
根据数据处理结果显示,CPI时序图具有显著的趋势,则该序列为典型的非平稳序列,因此可以考虑应用ARIMA模型(表3)来提取序列季节效应和长期趋势信息以达到提高模型拟合精度并进行计量分析与预测的目的。本文运用SPSS软件对CPI时间序列进行模型选择与预测,结果见表4和图3。

表3 模型描述

表4 模型统计量

图3 CPI序列的拟合效果图
根据表3输出结果可知,基于安徽省实际CPI数据,我们选择了乘积季节模型为ARIMA(1,1,12)(1,0,0)的模型。表4中Ljung-Box检验统计量Sig.>0.05,因此我们认为该模型拟合的残差序列通过了白噪声检验,消除了原序列长期趋势和季节效应的影响,说明了构建的乘积季节模型对序列相关信息提取充分是显著有效的。由图3可以看出,CPI序列拟合值与其观测值变化趋势基本一致,说明该模型拟合效果理想。因此,应用该模型对安徽省公布的CPI实际数据进行分析与预测是合理有效的,能够为宏观经济调控提供可靠的技术支撑。下面对安徽省部分CPI数据进行了拟合比较,2017年12月至2018年5月的拟合情况见表5。由预测图3和表5可发现此拟合模型预测结果良好,能够用于安徽省CPI的分析与预测,预测情况见表6。
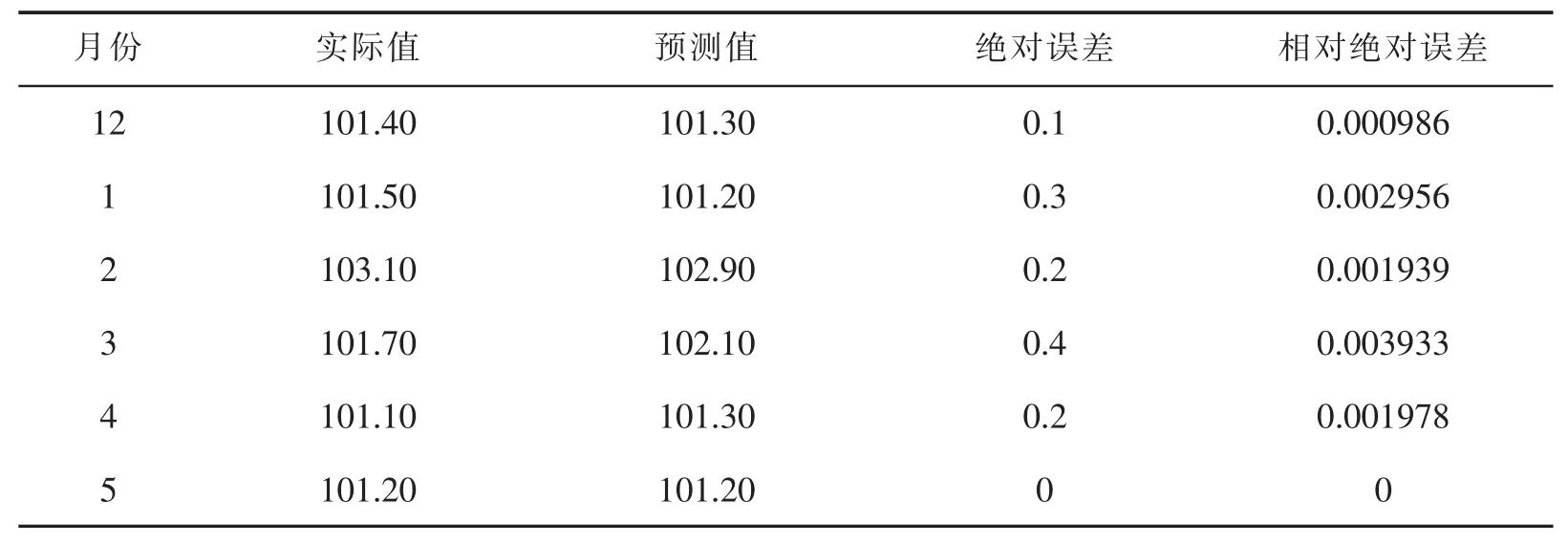
表5 2017年12月至2018年5月安徽省CPI拟合比较

表6 2018年6月至11月安徽省CPI模型预测结果
3.3 结果分析
根据图3预测结果显示,安徽省居民消费价格指数从2010年1月至2011年7月开始逐步上升到最高点,接着快速下滑直到2012年7月达到较低点,此时安徽省处于通货紧缩的状态,物价水平不稳定。直到2018年5月,居民消费价格指数缓慢回升、来回波动,且波动范围较小,逐渐趋于稳定。这是由于消费者的信心逐渐回暖,另外相关政府部门采取了积极有效的宏观调控措施,让CPI能够维持在一个相对稳定的水平,有效控制了物价指数。
依据此模型对安徽省2010年1月至2018年8月的实际CPI数据的预测结果能够发现,预测值接近真实值,拟合度较高。从表6能够看出未来安徽省2018年9月份的CPI数值将会持续上升,达到一个较高水平后,10月份有所回落,11月份将继续上升。这可能与市场经济的外部因素有关,比如中美贸易摩擦的不断升级,导致物价上涨较快,但10月份这种情况将得到缓和。由于居民消费价格指数进一步呈现出上升趋势,可能会带来通货膨胀的风险;为了使得物价处于一个合理的水平,相关政府部门应该加强宏观经济调控的力度。
4 结束语
本文依据安徽省2010年1月至2018年8月的实际CPI数据,构建了乘积季节模型,即基于ARIMA(1,1,12)(1,0,0)的居民消费价格指数预测模型。由实证分析的结果来看,此模型充分考虑了序列长期趋势效应、季节效应和随机波动之间的复杂交互影响,充分提取了CPI序列相关信息。模型的CPI预测值和实际观测值的绝对误差以及相对绝对误差向零值逼近且对应数值都比较小,说明此模型拟合的情况良好。应用该物价指数模型来分析和预测安徽省CPI的变化趋势及内在统计规律,具有良好的实际应用价值。
