基于单轴地磁信号的滚转角及转速解算*
2018-03-26张嘉易郝永平张继发
刘 英, 张嘉易, 郝永平, 孙 林, 张继发
(1.沈阳理工大学 现代教育技术中心,辽宁 沈阳 110159; 2.沈阳理工大学 CAD/CAM研究中心,辽宁 沈阳 110159)
0 引 言
在利用磁阻传感器进行导航的技术中,需要对受到干扰的采样信号进行实时处理。目前,国内应用磁阻传感器测姿进行了许多研究工作,如:针对地磁测量信号中含有的噪声特点,提出了将形态滤波与Hilbert-Huang变换结合起来,先低通滤波,再重构的方法[1];应用三维磁阻传感器采集地球三维磁场强度进行导航的方法[2];在保证旋转体制导方式高度自主的前提下引入了地磁信息,研究适用于大动态范围的旋转弹姿态测量算法[3]。在地磁信号处理中,均值滤波和中值滤波均为非常重要的滤波器,具有广泛的应用。如:利用包络均值滤波算法实时检测微弱信号[4];野外探测数据易受多种干扰影响,采用均值滤波和小波变换处理,可获得平滑的规律曲线[5]。但目前关于利用低成本单轴磁阻器件解算旋转体转角及转速的研究较少。
低成本地磁器件输出信号精度差,器件间电压幅值偏差较大,利用高斯公式解算旋转体转角会产生很大误差,导致部分象限无角度值。对环境干扰特别敏感,使部分采样点数据失真,有时产生采样电压在0~3.3 V的两端截止等现象。针对该低成本器件组成的处理系统,采用常规多轴采样信号解算旋转体对地转速、转角具有计算速度、内存等限制,难于实现。
本文提出了一种基于低成本单轴地磁基本采样信息直接解算旋转体对地转速、转角的新方法。采用单轴地磁传感器TMR2103检测旋转体地磁信息,利用STM32单片机进行信号处理与实时解算。该方法在均值去噪的基础上,直接进行采样数据的零点和周期实时解算,实现对旋转体滚转角实时预测,并分析了非匀速旋转体采样信号的变周期处理方法。
1 测试原理
单轴地磁传感器旋转体对地转速、转角测量机构原理如图1(a)所示,图1(b)为测量机构实验装置,电机产生旋转运动力矩通过联轴器带动滑环和旋转体一起转动,定角度套筒选择某一测量角度固定不动,旋转体通过光电传感器反馈固定角取值脉冲。旋转体内部的单轴地磁传感器测量地磁信号,通过单片机进行实时角度解算,当光电传感器反馈固定角取值脉冲为上升沿时返回旋转体解算角度,保存于STM32地址内存中,在连续测量过程中通过滑环信号线实时读取地磁测量解算角度值。
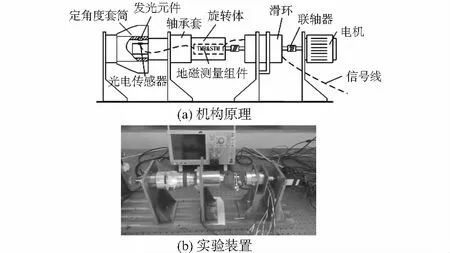
图1 测量机构
2 旋转体滚转角解算方法
采用均值滤波去除干扰信号,并对均值滤波进行了改进,在此基础上,实时计算采样信号均值线、均值点及角度零点,从而确定地磁信号周期,预测下个信号的角度值。
2.1 实时均值滤波
传统的均值滤波算法较占内存,且运算效率低。因此,采用少量数组X1[i](i≤10)和数组序号i进行滤波累加运算。
2.1.1 信号有效值确定及初始滤波
由旋转体采样特性推知,最高转速20 000 r/min时,采样数m>400。如图2所示,地磁信号近似正弦信号,可表示为f(t)=Asint+g(t),其中,t为采样时间,A为理论地磁信号电压幅值 3.3 V,g(t)为随机干扰信号。无干扰情况下f(t)=Asint,两采样点间的电压最大差值ΔVmax,即df(t)/dt极大值,可由f(t)=Asint=0求得t=kπ时电压差为最大值ΔVmax,对于离散形数字信号有
ΔVmax=A(sin(kπ+Δt)-sinkπ)=Asin Δt
(1)
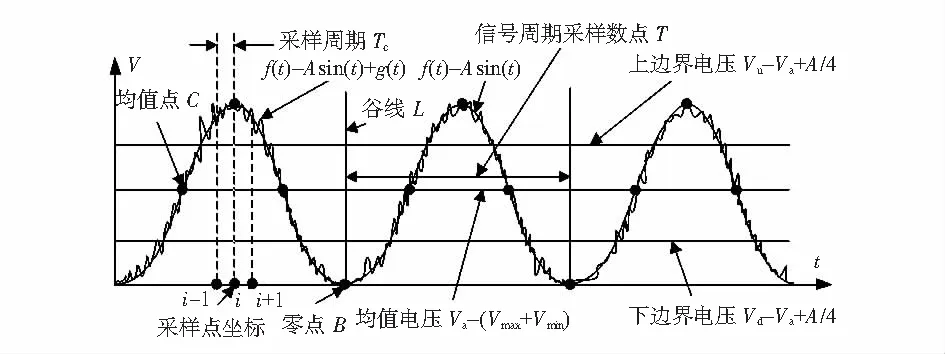
图2 地磁信号
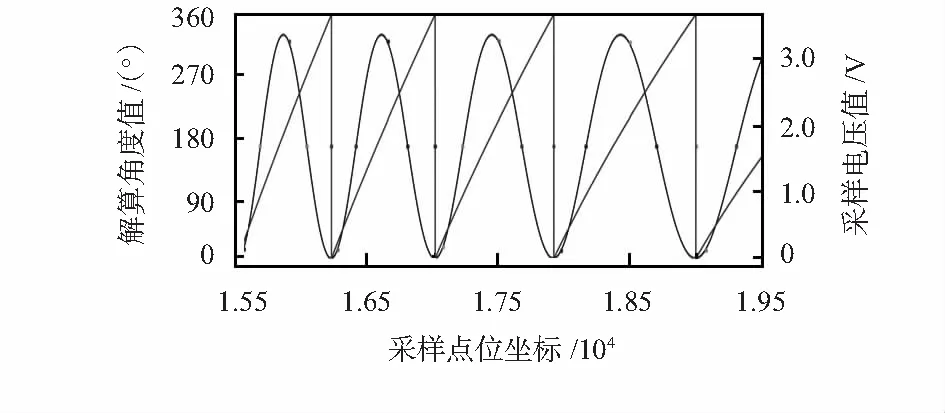
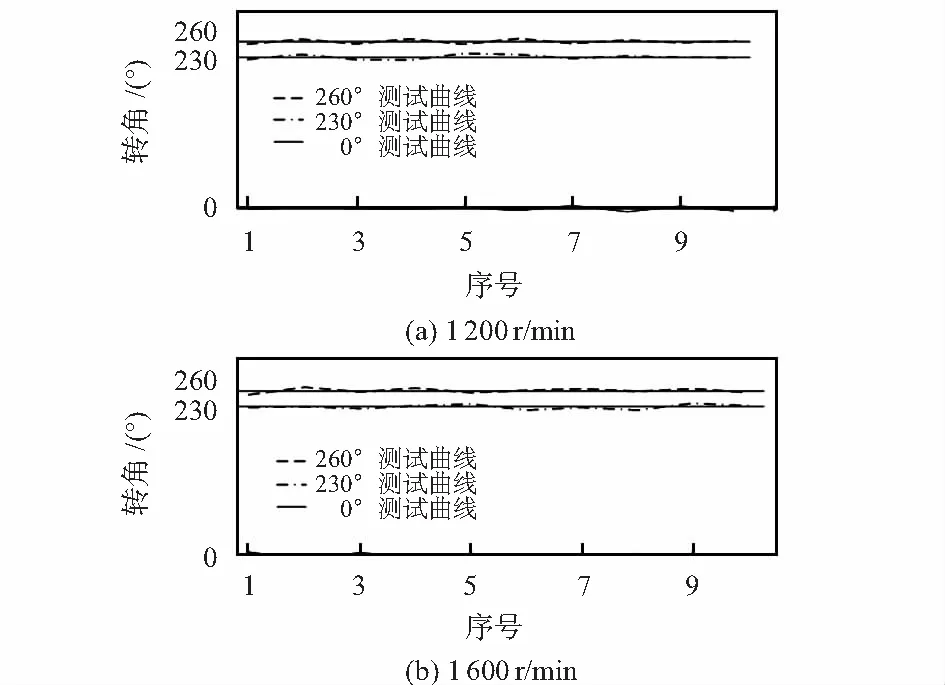
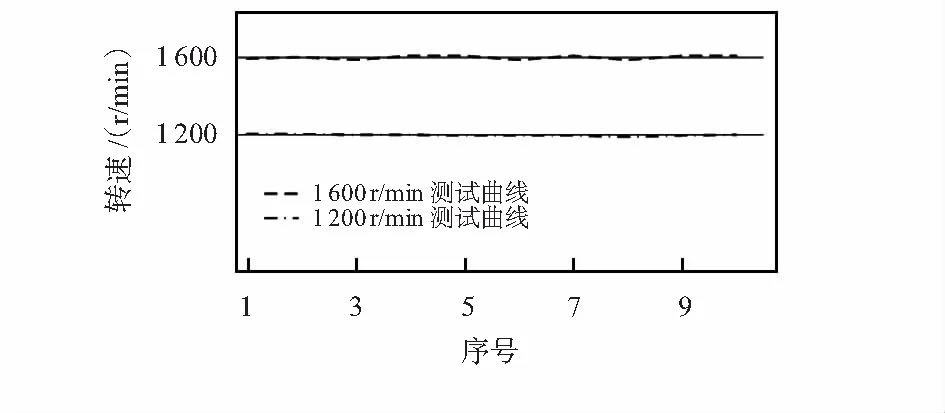
由采样数m>400知,ΔVmax=Asin Δt S=∑X1[i],1≤i≤10,U=S/N (2) S初值为0,每加一点i=i+1,计算两点差值D1[i]=|X1[i]-X1[i-1]|。将初始的10点中,除第一点外,满足D1[i]>ΔVmax且D1[i-1]>ΔVmax的点X1[i-1]值修改为临近点值后计算均值U,令i=1逐点推进均值计算。逐点滤波有效区域值确定为 ΔV=6×ΔVmax=0.345 (3) 若下一个的地磁信号值X1[i]=f(t)与当前均值的差值|X1[i]-U|>ΔV,则为无效信号;若|X1[i]-U|<ΔV,则为有效值。 2.1.2 均值滤波 在逐点推进均值算法中,每当检测到一个新的地磁信号f(t),首先判断|f(t)-U|是否大于ΔV,若是,则认为该地磁电压失真,用前一个电压值替换X1[i];否则,X1[i]=f(t)。以此类推,进行采样信号的实时均值滤波。总体均值滤波算法流程如图3所示。 图3 均值滤波算法流程 为减少内存占用并提高逐点累加计算速度,初始滤波后得到第一个均值点,令i=1,用下一个有效地磁信号替换数组X1[i]=f(t),i=i+1,以此类推。均值计算公式可简化为 U=U+(f(t)-X1[i])/N,1≤i≤10 (4) 图4为利用该算法获得的滤波效果。滤波后地磁电压信号误差控制在了0.057 V内。 如图2所示,采用计算地磁信号一周期采样点数T和零点C的解算方法实时预测旋转体的转速和转角。首先,根据转速范围(低速500~1 500 r/min,中速1 500~6 000 r/min,高速6 000~20 000 r/min),调整采样周期Tc使地磁信号周期采样点数控制在350~1 400之间。对初始的1 500个采样点进行最高电压Vmax和最低电压Vmin搜索。搜索策略是通过对实时计算的逐点累加电压均值U进行对比,求得Vmax和Vmin,进而求得均值线电压Va=(Vmax+Vmin)/2,幅值电压差A=Vmax-Vmin。由于地磁信号幅值是变化的,因此,在整个解算过程中Va,A的值要实时逐点搜索。 图4 均值滤波效果 如图2所示,在求得Va后,可计算上边界电压Vu和下边界电压Vd,由于采样周期固定,因此,可用X[k]=f(t)且k=p;k∈N表示第一个搜索到的满足Vd (5) 令峰值后的均值点C的采样点坐标为j1,谷值后的均值点C的采样点坐标为j2。谷线位置的采样点坐标jL为 jL=floor[(j1+j2)/2] (6) 标定旋转体角度时,令地磁信号谷底最低点对应的旋转体角度为0°,即B为零点(定义为旋转体零角度位置点)。如图2所示,两个谷线之间的采样点坐标数差值等于地磁信号一周期(即旋转体每转)采样点数量T。由于采样周期为定值,因此,对于匀速转动的旋转体,可利用已计算的周期采样点数T和当前谷底零点坐标jL实时解算旋转体滚转角度,即当前地磁采样信号k对应的角度α为 (7) 为适应周期T的实时变化和k值过大溢出,在搜索过程中每搜索过一个周期就更新T值,且令k=k-T,jL=jL-T,使0≤jL≤2T。 图5为利用该算法获得的滤波后地磁信号转角解算值曲线。图5(a)曲线为上端截止下部变形的地磁采样信号,折线为计算出的各采样点角度值;图5(b)曲线为幅值较小的地磁采样信号,折线为计算出的各采样点角度值。从图5的解算曲线结果来看,算法避免了地磁信号幅值和波形变化的影响,具有较强的容错能力。 图5 地磁转角解算值曲线 本文地磁采样周期Tc为根据转速范围预设的固定值,所以当计算出旋转体每转地磁信号采样点数T时,旋转体转速n(r/min)和ω((°)/s)由式(8)计算 (8) 旋转体在受外力矩作用时,会产生转速变化。假定外力矩为匀力矩M,M在角度α内做功Mα等于旋转体能量变化 (9) 考虑每两转i和i+1之间谷线位置的转速有 (10) (11) (12) 因此,可利用已搜索出的各周期谷线位置信号周期采样数倒数的平方差计算下一信号周期采样点数Ti+1。对于变化力矩M可由式(11),利用Qi-k~Qi-1的已知数据,用最小二乘法拟合Qi-k~Qi-1的规律曲线计算Qi,进而求得Ti+1的值代入式(7)和式(8),计算当前信号周期内采样点的转速和转角。 图6为利用该算法获得的变周期地磁信号转角解算值曲线。曲线为变周期地磁采样信号,折曲线为计算出的各采样点角度值。解算结果表明:算法可以对变周期地磁信号进行实时角度解算。 图6 变周期地磁信号的转角解算 利用图1(b)的实验装置对0°,230°及260°的固定角度分2种转速进行实时测量与解算。当固定套筒角度一定时(0°,230°,260°),根据转速设定Tc= 0.106 ms;启动旋转电机,运行单片机地磁信号实时角度解算程序;当光电传感器扫过光幕时,产生脉冲信号,根据是否产生中断读取当前解算预测的角度值。图7(a)和图7(b)为旋转体分别在1 200 r/min与1 600 r/min转速下,固定套筒角度取0°,230°和260°时,测量的旋转体滚转角度实时解算值曲线。 图7 不同转速下旋转体滚转角度实时解算值曲线 图8为旋转体分别在1 200 r/min转速与1 600 r/min转速下,固定套筒角度分别取0°,230°和260°时,测量的旋转体转速实时解算值曲线。 图8 旋转体转速实时解算值曲线 实验结果表明:方法原理可行,能够实现低成本磁阻器件的旋转体滚转角度和转速的实时解算。如果采用较好的地磁器件和高速大内存的处理器芯片,解算精度会有较大的提高。 提出了基于单轴地磁传感器的旋转体滚转角与转速的实时解算方法,实验分析表明:角度解算单边误差小于6.3°,转速解算误差小于0.81 %,说明利用本文方法可以实现对单轴磁阻器进行旋转体滚转角度和转速的实时解算,对于降低测量成本具有实际意义。 [1] 李 季,潘孟春,唐 莺,等.基于形态滤波和HHT的地磁信号分析与预处理[J].仪器仪表学报,2012,33(10):2175-2180. [2] 李文胜,管雪元,姜博文.基于磁阻传感器的地磁数据采集装置[J].传感器与微系统,2017,36(2):104-106. [3] 李兴城,牛宏宇.基于磁阻传感器的旋转弹姿态测量算法研究[J].计算机仿真,2012,29(5):51-54,85. [4] 叶卫东,李行善.包络均值滤波算法实时检测微弱信号[J].北京航空航天大学学报,2010,36(8):909-912,926. [5] 吴 巧,闫 述.均值滤波和小波变换在瞬变电磁信号处理的应用[J].数据通信,2013(6):33-35,43.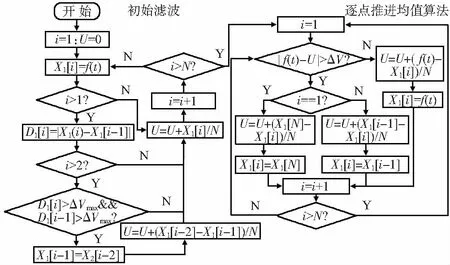
2.2 零点标定及转角和转速解算



3 变周期处理方法分析

4 实验验证
5 结束语
