无线充电式传感器系统设计及关键技术*

谢国民， 韩刘路， 付 华， 丁会巧

(辽宁工程技术大学 电气与控制工程学院，辽宁 葫芦岛 125105)

0 引 言

无线电能传输技术摆脱了传统有线传输对金属导线依赖[1]，更加灵活、方便地实现了能量的不接触转移。该技术不仅已经用于矿井、水下作业、电动汽车、医疗设备、家用电器等各个领域，而且对电磁学的发展具有促进作用[1～4]。近年来，特别是应用电磁共振式多负载无线电能传输越来越多，成为了当前研究的热点。

然而，该技术有仍有许多不足之处[5]，且在当前共振式无线电能传输技术的研究中，对多负载的空间位置问题缺乏具体分析，文献[6]分析了改变角度偏移对耦合因数的影响，仅对单负载传输系统进行研究。文献[7]对两个负载线圈的情况进行了研究，但均考虑同轴情况，未考虑线圈的方向和距离对系统功率、效率的影响。文献[8，9]分析了方向对双负载系统的影响，却未针对角度的具体变化分析影响效果。

本文采用双负载系统模拟同时对多个传感器进行传输的情况，研究偏移角度、最佳距离和双负载无线电能传输系统功率、效率的变化规律，并设计了无线电能传输实验系统，验证所提结论。

1 谐振式无线电能传输系统分析与建模

双负载电磁共振式无线电能传输系统的等效电路模型如图1所示，模型基于近场强耦合的概念，在发射线圈和2个接收线圈间保持相同的谐振频率实现能量的高效传输。

图1中，功率源US为具有一定的功率的高频电压源，作为无线输电的能量输入源；发射端线圈为LS，其高频下的内阻值为RS(S代表发射端)，CS为其谐振电容值；Ld1，Ld2为接收端线圈，Rd1，Rd2分别为其高频下的内阻值，Cd1，Cd2为谐振电容值；RL1，RL2为接收回路的负载；LS与Ld1，Ld2之间的互感为M12，M13;Ld1，Ld2之间的互感为M23。

图1 谐振式无线电能传输系统电路模型

发射线圈和2个接收线圈之间存在互感，而2个接收线圈间存在交叉耦合。其等效电路可以表示为耦合电感电路，如图2所示。

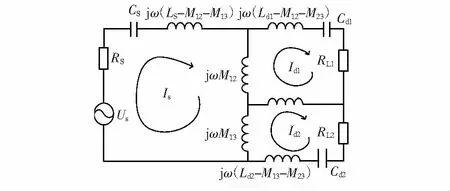
图2 两接收线圈间的互感等效电路

等效电路中，IS，Id1，Id2为发射系统和双接收系统的电流，列KVL方程可得

(1)

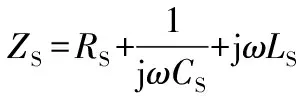
(2)

(3)

(4)

可以得到各回路的电流值

(5)

(6)

(7)

根据式(7)发射端的电流公式，简化系统电路图，即将接收端反射到发射端。简化的电路如图3。

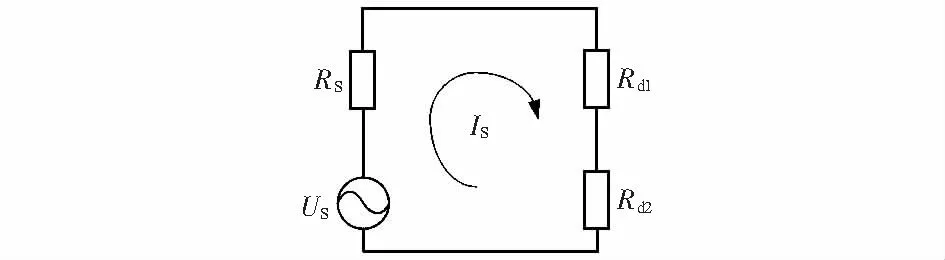
图3 简化的系统等效电路

两接收端获得的能量为

(8)

通过对互感模型的分析,系统效率等于输出功率和输入功率的比值，双负载系统的输出总功率、效率表达式为

(9)

2 空间位置对系统参数的影响

为了更确切描述空间位置和互感M的关系，引入了诺埃曼的二重积分公式[10]

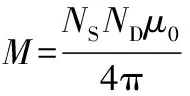
(10)

式中NS,ND为发射线圈和接收线圈的匝数；IS,ID为各自线圈的电流；rSD为距离相对标准方差可以通过几何方法评估；μ0为真空磁导率。

为了研究方便，图中只显示发射线圈和接收线圈，图4中，d为两个线圈的距离，θ和Φ为收发线圈参数方程的参数，Δ为位移的径向距离，而α是位移的偏转角度。保持发射线圈不变，调整接收线圈的空间位置。图4中的情况是认为是一般状态，根据空间几何分析，可以将dIS和dID及距离表示[11]

dIS=rS(-sinθx+cosθy)dθ

(11)

dID=rD(-sinφcosαx+cosφy+sinφsinαz)dφ

(12)

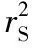
(13)

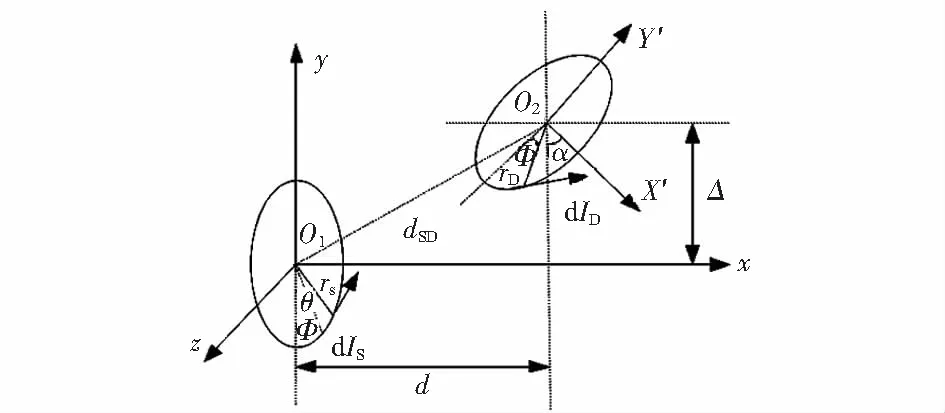
图4 无线电能传输系统的两线圈任意位置示意

将式(11)～式(13)代入式(8)中可以表示为

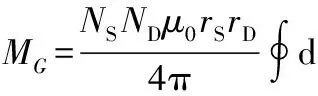
(14)

由式中可以清晰看到，径向距离Δ的下降速度较快，而α偏转角度的下降幅度比较舒缓，说明互感值对径向距离的变化更加敏感。当收发线圈之间存在合适的偏移角度时，不但不会减弱互感，反而可以增强收发线圈之间的耦合，使互感更大。

两负载线圈和源线圈同轴时，可以忽略两接收线圈的互感，即M23=0，认为M12=M13=M，当频率、线圈尺寸等参数确定时，令有功功率P对互感M求导，满足以下条件时

(15)

P有且仅有一个极大值，此时X1=0，X2=0。而对接收线圈的感抗X1，X2的效率进行分析，可以发现在发射线圈发生谐振时，只有两接收线圈同时谐振时，效率达到最大值。

当负载线圈存在一些角度时，此时的互感M23≠0，为了降低系统设计时的复杂性，将发射和两个接收线圈设计成相同的尺寸和结构，即，认为两线圈具有相同的等效参数。而偏转角度β1=arctan(Δ/d)，可以计算出源线圈和双负载线圈之间的互感

d1x=

(16)

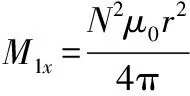
x=2,3

(17)

3 数据仿真分析

为了论证系统距离和偏转角度对系统的影响问题，使用仿真软件HFSS创建系统模型。谐振线圈半径R=30 cm、高度h=14 cm、匝数N=15，铜线半径a=2.2 mm，如图5所示。

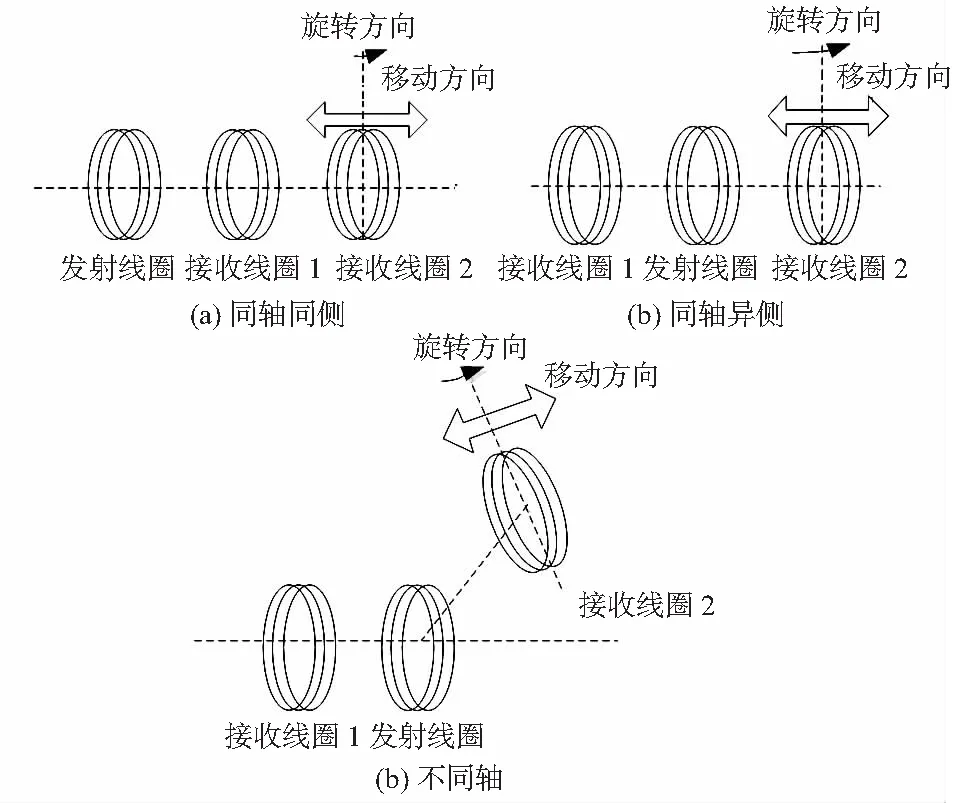
图5 3种情况下系统模型

在线圈参数给定情况下，线圈互感对线圈效率起到决定性作用。图6为互感随着角度和距离改变的变化情况。

图6 双负载线圈互感随偏转角度和距离的变化曲线

当接收端的两个线圈只存在径向距离和角度时，互感随两个线圈之间的角度增加而下降，当两个线圈呈90°的时候，接收线圈之间的互感已很小且随轴向距离的变化下降很缓慢。

4 实验验证与分析

为了验证理论的正确性，设计了一种磁耦合谐振式无线电能传输的实验系统。系统由电源、发射系统和接收系统组成，采用IR2110作为信号发生器。通过阻抗分析仪WK6500B得到电压值，然后由输入电流、电压值，可得系统的传输效率。实验所使用传输系统的发射线圈与接收线圈参数一致，结构对称。系统各项参数配置：系统频率f为202 kHz,输入电压U为24 V，线圈匝数N为14，半径r为11，导线线径a为2.2，发射端电感LS为66.15 μH，接收端1电感Ld1为66.30 μH，接收端2电感Ld2为66.35 μH，发射端电容CS为15.42 nF，接收端1电容Cd1为15.21 nF，接收端2电容Cd2为15.13 nF。

1)处于发射线圈两侧的单个接收线圈的距离特性验证：保持其他参数不变，通过测量负载电压，得出此时的功率、效率值。当系统其他参数确定时，随着轴向距离的增大系统的传输功率先增加后减少，系统的传输效率线性下降。参数配置完全时,最大功率在距离d≈14 cm实现，综合考虑系统功率和效率，在距离dMAX时可以取得最优值。

2)系统功率验证：由于单负载系统，存在最佳距离使功率值最大。考虑不同情况对负载线圈L1的最佳距离的影响，如图7，可以看出同单负载系统相比较，双负载系统的同轴异侧和同轴同侧情况，虽然整体功率降低，但最大功率对应的最大距离值增加。而在存在偏转角度的情况，最佳距离值约为19 cm。说明选择合适的偏转角度不仅能使功率值增加，还能提高最佳距离值。

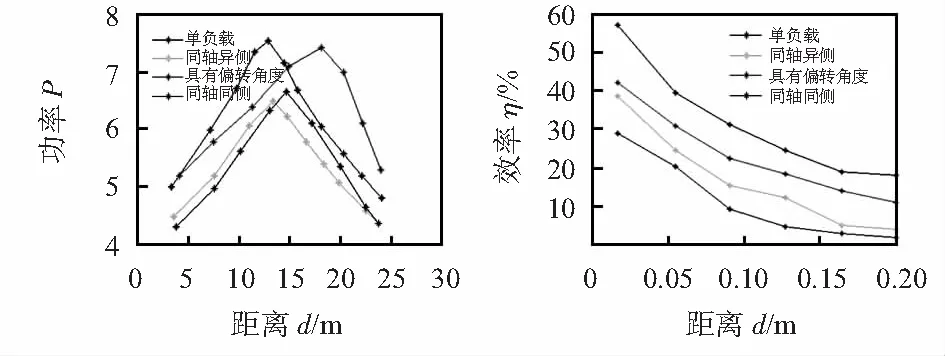
图7 接收线圈L1的功率和效率随距离变化曲线

3)接收部分旋转验证：两个接收线圈和磁场的相对空间关系会发生变化，接收线圈的平面法向将出现和磁场方向不平行甚至垂直的情况，则接收线圈中的电能会随两线圈空间位置的变化而变化。保持接收线圈的轴向距离不变，则收发线圈间的系统效率随偏转角度的变化如图8所示。

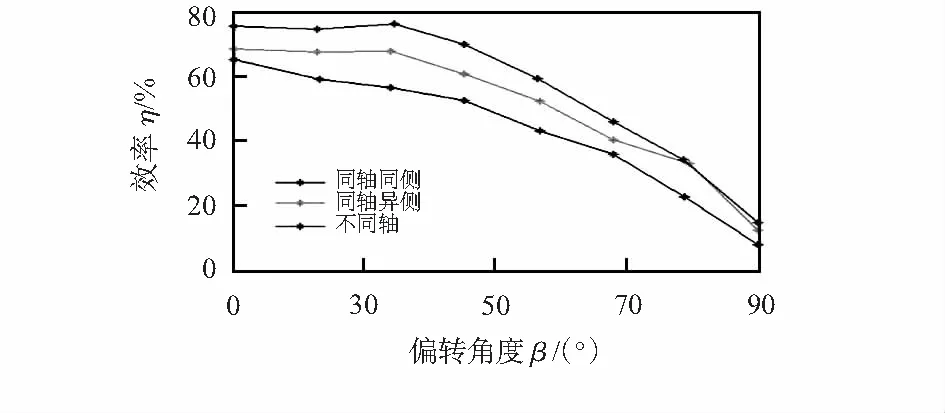
图8 系统传输效率随偏转角度变化曲线

磁耦合谐振式系统具有较强的方向性，当线圈偏转角度发生改变，系统的传输效率会发生变化。使系统距离保持在功率、效率的最大值，改变偏转角度。当同轴同侧，同轴异侧时，接收线圈发生角度变化，在大致角度为35°时，效率可实现最高值52 %。当不同轴时，在角度为30°时可达到最大效率57 %。

5 结 论

对单、双负载磁耦合谐振式无线电能传输系统的空间变化量进行对比分析和研究。分析了在同轴异侧、同轴同侧以及出现偏转角度3种情况下对功率、效率的影响。研究结果表明：

1)通过在两侧布置负载线圈，并合理控制参数，在距离dMAX时系统功率效率可以取得最大值；

2)随着两接收线圈的角度偏转，选择最优角度能使系统的效率最优；

3)运用控制变量法，当距离保持最大值，合适的角度偏移不但不会减弱能量的传输，反而可以增强收发线圈之间的耦合。

[1] 李求实,陈 彬.线性无线传感器网络应急应用优化[J].传感器与微系统,2012,31(10):68-69.

[2] 杨庆新,章鹏程,祝丽花,等.无线电能传输技术的关键基础与技术瓶颈问题[J].电工技术学报,2015(5):1-8.

[3] 徐晨洋,张 强,李 岳,等.体内植入装置的磁耦合谐振无线电能传输分析[J].传感器与微系统,2016,35(10):49-51.

[4] Kim J W,Son H C,Kim K H,et al.Efficiency analysis of magne-tic resonance wireless power transfer with intermediate resonant coil[J].IEEE Antennas and Wireless Propagation Letters,2011,10:389-392.

[5] 黄学良,谭林林,陈 中,等.无线电能传输技术研究与应用综述[J].电工技术学报,2013(10):1-11.

[6] 李 阳，杨庆新，严 卓，等.磁耦合谐振式无线电能传输方向性分析与验证[J].电工技术学报,2014,29(2):197-203.

[7] 张 波，张 青．两个负载接收线圈的谐振耦合无线输电系统特性分析[J]．华南理工大学学报：自然科学版，2012(10)：152-158．

[8] 陈文仙,陈乾宏,张惠娟.电磁共振式无线电能传输系统距离特性的分析[J].电力系统自动化,2015(8):98-104.

[9] Yin N，Xu G Z，Yang Q X，et al．Analysis of wireless energy transmission for implantable device based on coupled magnetic resonance[J]．IEEE Transactions on Magnetics，2012，48(2):723-726．

[10] 刘修泉,曾昭瑞,黄 平,等.空心线圈电感的计算与实验分析[J].工程设计学报,2008(2):149-153.