icMRCI+Q 理论研究BF+离子电子态的光谱性质和预解离机理∗

邢伟 孙金锋 施德恒 朱遵略

1)(河南科技大学材料科学与工程学院,洛阳 471023)

2)(信阳师范学院物理电子工程学院,信阳 464000)

3)(河南师范大学物理与材料科学学院,新乡 453007)

1 引 言

BF3等离子体在半导体制造中用于硅晶片的离子掺杂,其中,BF+是BF3等离子体中重要的组成成分[1].实验上,BF+离子产生于光电离过程B2F4+hν→BF++BF3+e[2].为了更好地理解这个反应过程,人们对BF+离子电子态的光谱信息进行了实验[3−5]和理论研究[5−12].

实验方面,主要研究了BF+(X2Σ+)←BF(X1Σ+)电离的垂直电离势(VIP)、绝热电离势(AIP)和BF+(X2Σ+)的光谱常数. 早在1963年,Robinson[3]采用发射光谱技术估算BF(X1Σ+)的第一电离势为10.9726 eV.1970年,Caton和Douglas[4]研究了90—1100 nm范围内BF分子高分辨率的发射和吸收光谱,基于110 nm附近的0-0波带报道了BF分子精确的AIP为(11.115±0.004)eV,从BF分子接近电离限的一系列里德伯态计算获得BF+离子X2Σ+态的平衡核间距(Re)、振动量子数υ′′=0与υ′′=1的能级间距(ΔG1/2)和平衡转动常数(Be)分别为0.121 nm,1680 cm−1和1.64 cm−1.随后,Hildenbrand[2]采用电子碰撞质谱分析方法获得了BF+(X2Σ+)←BF(X1Σ+)电离的VIP为(11.06±0.10)eV.1983年,Dyke等[5]利用高温光电子能谱观察到BF+(X2Σ+)←BF(X1Σ+)电离对应的0-0波带,获得了AIP为(11.12±0.01)eV以及BF+(X2Σ+)的离解能(De),Re和振动频率(ϖe)分别为(5.09±0.14)eV,(0.1208±0.0005)nm和(1765±20)cm−1.

理论方面,早期的研究主要在Hatree-Fock自洽场(HF SCF)[5−8]级别获得BF+离子X2Σ+,12Π和22Σ+态的光谱常数和VIPs,而且VIPs[5,6,8]都是从BF分子X1Σ+态Re处开始计算,没有考虑零点能修正、相对论效应和电子的关联效应. 直到1982年,Rosmus等[9]利用多参考组态自洽场方法和高斯型轨道基组计算了包括BF(X1Σ+)和BF+(X2Σ+)的势能曲线(PECs),并得到其相应的光谱常数. 1999年,Bauschlicher和Ricca[10]在基于密度泛函理论的B3 LYP/6-311+G(2df)下研究了BFn(n=1—3),BF+n(n=1—4),BCln(n=1—3)和BCl+n(n=1—3)的电子结构,并利用单、双重和三重微扰耦合簇[CCSD(T)]方法获得VIP,AIP和D0.两年后,Bruna和Grein[11]利用多参考组态相互作用(MRCI)方法结合原子轨道基组研究了MX±(M=Be,B,Mg,Al;X=N,O,F,P,S,Cl)分子离子X2Σ+态的Re以及12Π和22Π态的垂直激发能.最近,Magoulas等[12]在0.079—0.424 nm的核间距范围内,利用考虑Davidson修正的MRCI方法结合相关一致基aug-cc-pV6Z(AV6Z)基组计算了BF+离子前两个离解极限B+(1Sg)+F(2Pu)和B+(3Pu)+F(2Pu)的能量间隔、8个束缚Λ-S态的PECs,又采用部分自旋匹配的CCSD(T)理论[RCCSD(T)]和aug-cc-pCV5Z-DK基组计算X2Σ+态的PEC,并拟合得到相应的光谱常数.总结现有的实验和理论计算,我们发现:1)对于BF(X1Σ+)的VIPs和AIPs, 仅Bauschlicher和Ricca[10]采用CCSD(T)方法计算BF+(X2Σ+)←BF(X1Σ+)的AIP时考虑了核价相关修正、标量相对论修正和零点能修正;2)对于BF+前两个离解极限B+(1Sg)+F(2Pu)和B+(3Pu)+F(2Pu)所对应的14个Λ-S态,现有的实验和理论计算主要集中于研究X2Σ+态的光谱常数;对于其他的13个激发电子态(12Π,12Δ,22Σ+,32Σ+,12Σ−,22Π,32Π,14Π,24Π,14Σ+,24Σ+,14Δ和14Σ−), 只有Nesbet[7]和Magoulas等[12]计算了12Π,22Π,22Σ+,12Δ和12Σ−态的PECs,并获得了其光谱常数.另外,Niu等[13]对与BF+具有相同价电子的BBr+的计算结果表明:此类离子体系电子态之间存在强的相互作用;然而,迄今为止未有任何实验和理论计算对BF+电子态之间的相互作用进行研究.众所周知,旋轨耦合效应在研究双原子分子离子电子态的光谱特性和电子态之间相互作用方面扮演着重要的角色[14−18].

本文采用高精度的、包含旋轨耦合效应以及核价相关、标量相对论修正和PECs外推至完全基组极限的量化从头算方法,深入地研究BF+离子前两个离解极限所对应的14个电子态的光谱特性.本文报道了BF分子X1Σ+态的VIPs和AIPs,BF+离子14 个Λ-S态(X2Σ+,12Π,22Π,22Σ+,14Σ+,14Δ,14Σ−,12Δ,12Σ−,32Σ+,14Π,24Π,24Σ+和32Π)及其所产生的30个Ω态[(1)1/2,(1)2Π3/2,(2)1/2,(3)1/2,(2)3/2,(4)1/2,(3)3/2,(5)1/2,(1)4Δ7/2,(1)4Δ5/2,(4)3/2,(6)1/2,(7)1/2,(5)3/2,(6)3/2,(2)2Δ5/2,(8)1/2,(9)1/2,(3)4Π5/2,(1)4Π−1/2,(7)3/2,(10)1/2,(11)1/2,(8)3/2,(12)1/2,(9)3/2,(13)1/2,(10)3/2,(4)4Π5/2和(2)4Π−1/2]的PECs,获得束缚以及准束缚态的光谱常数(激发能Te,De,Re,谐振频率ωe和非谐振动常数ωexe).研究各种曲线交叉和避免交叉现象,分析邻近的激发电子态对X2Σ+,22Π,32Σ+和32Π态的扰动. 计算14个Λ-S态和30个Ω态离解极限处的相对能量. 最后研究22Π—X2Σ+,22Σ+—X2Σ+,(3)1/2—(1)1/2势阱一和(2)3/2—(1)1/2势阱一的跃迁特性(上标势阱一代表(1)1/2Ω态第一个势阱).

2 计算方法

本文所有计算都是在MOLPRO 2010.1程序包[19]中进行的.BF+离子和BF分子都属于C∞v群,由于MOLPRO程序包的限制,在计算中须将其具有的C∞v群变换为C2v群.C2v群有4个不可约表示:A1,B1,B2和A2.C∞v→C2v的对应关系为:Σ+→A1,Π→B1+B2,Δ→A1+A2和Σ−→A2.在C2v群下,本文第一步计算BF分子X1Σ+态和BF+离子14个Λ-S态的PECs,在核间距0.0808—1.0608 nm的范围内,首先采用HF SCF方法分别得到BF分子X1Σ+态和BF+离子X2Σ+态的初始猜测分子轨道和波函,然后使用态平均的完全活性空间自洽场(CASSCF)方法对初始猜测分子轨道和波函进行优化,最后用内收缩MRCI+Q(icMRCI+Q)[20,21]计算BF分子X1Σ+态和BF+离子14个Λ-S态的PECs.需要指出的是我们利用态平均的CASSCF方法总共计算了BF+离子12个双重态(4个A1态、3个B1态、3个B2态和2个A2态)和9个四重态(3个A1态、2个B1态、2个B2态和2个A2态),并且每一个态用相同的权重因子0.05.这对应于C∞v群下BF+离子前两个离解极限B+(1Sg)+F(2Pu)和B+(3Pu)+F(2Pu)所包含的全部14个Λ-S态. 为保证Λ-S态PECs的计算精度,B原子、B+离子和F原子都采用较大的相关一致基aug-cc-pV5Z(AV5Z)和AV6Z[22,23]. 计算步长取0.02 nm,在Re附近,为获得PECs的细节信息,步长取0.002 nm.使用非收缩全电子相关的cc-pCVTZ(CVTZ)[24]基组计算核价相关的贡献(记为CV).使用三级Douglas-Kroll-Hess(DKH3)哈密顿近似[25,26]在cc-pV5Z基组水平上进行相对论修正(记为DK).在CASSCF及其随后的icMRCI+Q计算中,选择10个分子轨道(MO)作为活性空间,分别是4个a1,3个b1和3个b2轨道;B原子、B+离子和F原子的2s2p壳层的电子处于这个活性空间中.也就是说,BF分子的10个价电子和BF+离子的9个价电子分布在3—7σ和1—2π MO 上.其余的4个内核电子则放入2个闭壳层轨道(2a1)中,对应于BF分子和BF+离子的1—2σ MO.另外,B原子、B+离子和F原子1s闭壳层的4个电子用于核价相关效应计算.当进行冻结核计算时,B原子、B+离子和F原子1s闭壳层的4个电子被冻结.当采用这12个轨道(6a1,3b1和3b2)进行计算时,在目前的核间距范围内所得的PECs既光滑、又收敛.

完全基组极限时的总能量采取参考能和相关能分别外推公式[27]得到:

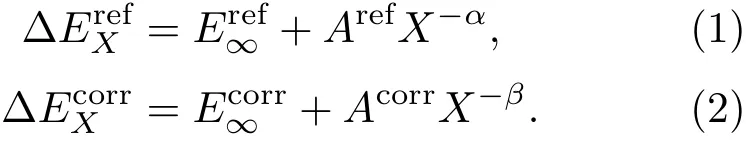
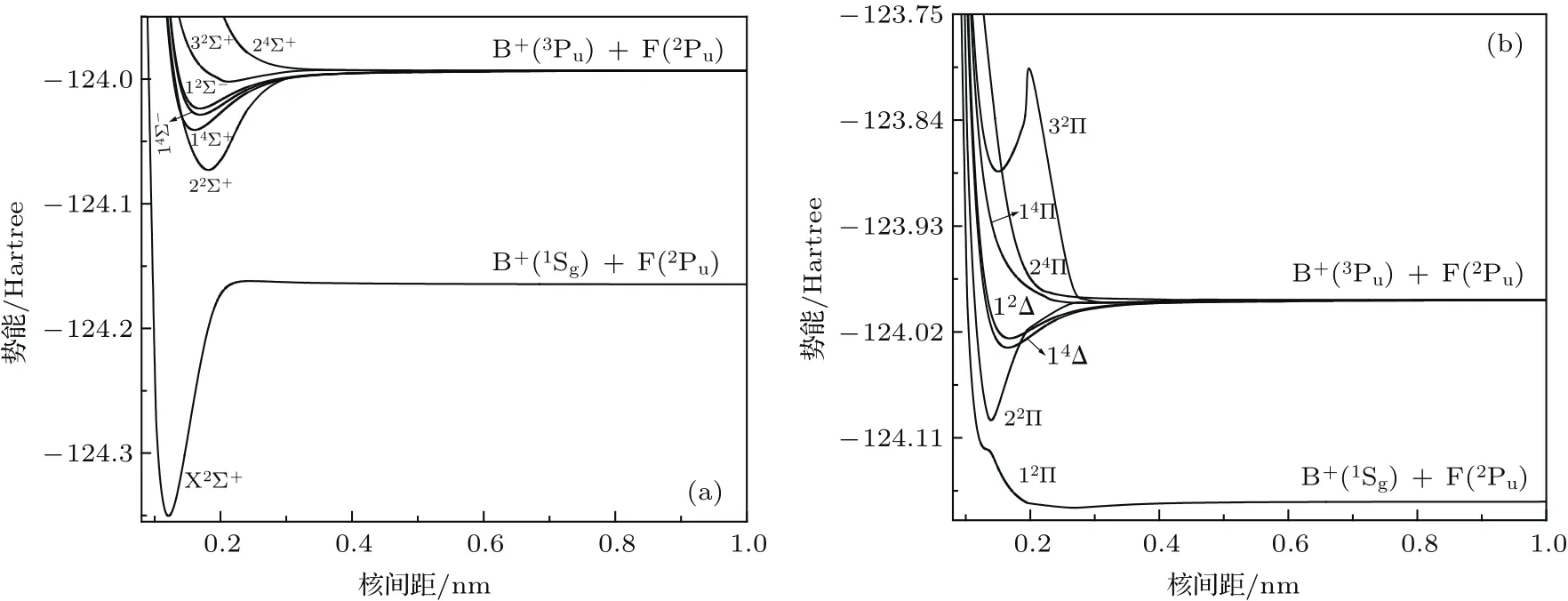
图1 BF+离子14个Λ-S态的PECs (a)7个Σ对称性的Λ-S态;(b)7个Π和Δ对称性的Λ-S态Fig.1.PECs of 14 Λ-S states of BF+cation:(a)7 Λ-S states with the Σ symmetry;(b)7 Λ-S states with the Π and Δ symmetries.

基于以上计算的Λ-S态和Ω态的PECs,利用LEVEL 8.0程序[28],通过求解原子核运动的Schrödinger方程,获得BF+离子束缚和准束缚的12个Λ-S态和28个Ω态的光谱常数.

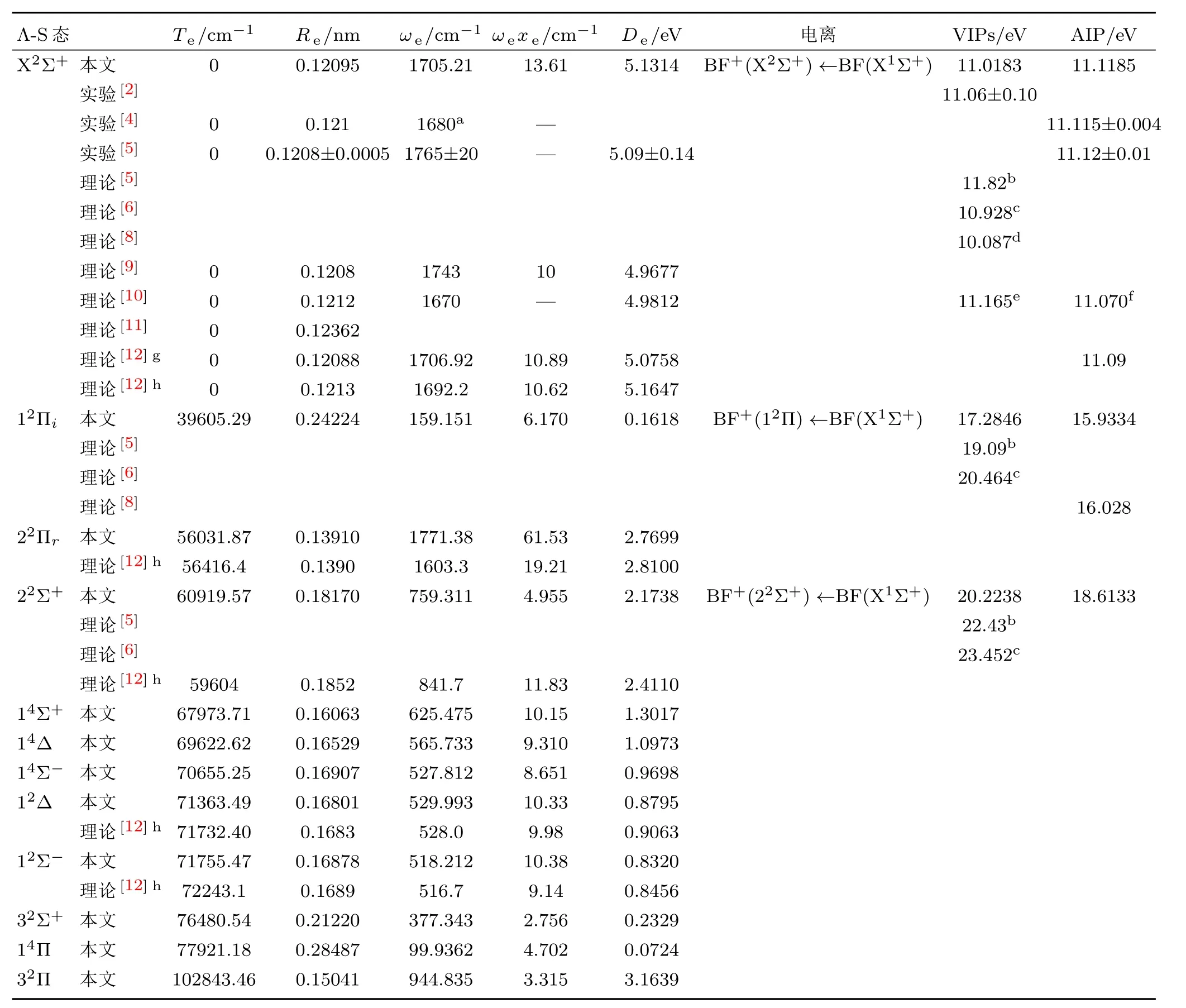
表1 icMRCI+Q/CV+DK+56理论水平上BF分子X1Σ+态的电离势和BF+离子12个Λ-S电子态的光谱常数Table 1.Ionization potentials for X1Σ+state of BF molecule and spectroscopic parameters of the 12 Λ-S states of BF+cation at level of icMRCI+Q/CV+DK+56.

3 结果与讨论

3.1 BF分子X1Σ+态的电离势

利用icMRCI+Q/CV+DK+56理论方法,在BF分子X1Σ+态几何构型下,获得了BF分子X1Σ+的VIPs, 在BF分子X1Σ+态和BF+离子X2Σ+,12Π和22Σ+态各自几何构型下,获得了BF分子X1Σ+的AIPs,并把本文计算的结果连同挑选的实验值[2,4,5]以及理论值[5,6,8,10,12]列入表1.

BF分子X1Σ+态的电子组态为1σ22σ23σ24σ21π45σ22π06σ07σ0,5σ轨道失去一个电子(5σ→∞)产生BF+(X2Σ+),本文计算得到的VIP和AIP分别为11.0183 eV和11.1185 eV,分别对应于BF+(X2Σ+,υ′′＜0)+e−←BF(X1Σ+,υ=0)+hν和BF+(X2Σ+,υ′′=0)+e−←BF(X1Σ+,υ=0)+hν的跃迁,由表1可知,没有理论结果比本文更接近实验值[2,4,5]. X1Σ+态1π轨道失去一个电子(1π→∞)产生BF+(12Π),本文计算得到的VIP和AIP分别为17.2846 eV和15.9334 eV,分别对应于BF+(12Π,υ′＞19)+e−←BF(X1Σ+,υ=0)+hν和BF+(12Π,υ′=0)+e−←BF(X1Σ+,υ=0)+hν的跃迁.BF分子X1Σ+态4σ轨道失去一个电子(4σ→∞)产生BF+(22Σ+),本文计算得到的VIP和AIP分别为20.2238 eV和18.6133 eV,分别对应于BF+(22Σ+,20＜υ′＜21)+e−←BF(X1Σ+,υ=0)+hν和BF+(22Σ+,υ′=0)+e−←BF(X1Σ+,υ=0)+hν的跃迁.

3.2 BF+离子Λ-S态的光谱常数

B原子和F原子基态的电离能分别为66928.01和140524.47 cm−1[29,30].因此,BF+离子的第一离解极限为B+(1Sg)+F(2Pu).B+离子第一激发态3Pu相对于基态1Sg的能级为37345.00 cm−1[31].利用这些电离能和能级,确定BF+离子的第二离解极限为B+(3Pu)+F(2Pu).利用分子群论理论,确定这前两个离解极限所产生的14个Λ-S态为X2Σ+,12Π,12Δ,22Σ+,32Σ+,12Σ−,22Π,32Π,14Π,24Π,14Σ+,24Σ+,14Δ和14Σ−. 在icMRCI+Q/CV+DK+56理论水平下,本文分别计算了B+(1Sg),B+(3Pu)和F(2Pu)的能量,并把本文计算的BF+离子前两个离解极限B+(3Pu)+F(2Pu)与B+(1Sg)+F(2Pu)的能量间隔连同实验值[31]以及理论值[12]列入表2.由表2可知,本文所计算的这两个离解极限的能量间隔与实验值[31]的偏离为96.34 cm−1(0.258%),明显优于Magoulas等[12]利用MRCI/AV6Z的计算结果,这表明本文的计算能很好地描述BF+离子的离解特性.

BF+离子X2Σ+态主要电子组态是1σ22σ23σ24σ21π45σ12π06σ07σ0(0.8570), 其他电子组态所占的权重很小.其势阱深度为41388.00cm−1,有33个振动态,本文计算的Re和De与实验值符合得很好. 它们与实验值[4,5]的最大偏离分别为0.00015 nm(0.124%)和0.0414 eV(0.813%);由表1可知,仅Rosmus等[9]获得的Re以及Magoulas等[12]在RCCSD(T)/aug-ccpCV5Z-DK理论水平计算的Re和De值比本文更接近实验结果[4,5]. 本文得到的ΔG1/2为1679.04 cm−1,仅比实验值[4]小0.96 cm−1.本文的ωe虽然比实验值[5]小59.79 cm−1,但与Magoulas等[12]在RCCSD(T)/aug-cc-pCV5Z-DK理论水平得到的结果接近.

表2 icMRCI+Q/CV+DK+56理论水平上获得的14个Λ-S态离解极限处的相对能量Table 2.Relative energies of the 14 Λ-S states in the dissociation limits at the level of icMRCI+Q/CV+DK+56.

X2Σ+态电子组态中一个电子从1π→5σ的激发产生12Π电子态,在核间距0.13910 nm附近,由于12Π态与22Π态的避免交叉,导致12Π态的PEC出现不光滑的点.另外,不同于文献[12]中12Π态为排斥态,本文计算的12Π态与BBr+的12Π态[13]相似,具有一个浅的势阱,势阱的深度和位置分别为1305.22 cm−1和0.24224 nm,包含19个振动能级(78.03,224.85,359.36,482.70,595.34,697.90,790.61,873.52,946.88,1010.98,1066.23, 1113.30, 1152.84, 1185.70, 1212.99,1235.23,1252.72,1266.49和1277.17 cm−1),由于其Re比X2Σ+态的Re大0.12129 nm,从而导致在Franck-Condon区域是排斥的,这给实验上观察这个态带来了很大的困难.X2Σ+电子组态中一个电子从5σ→2π的激发产生22Π态,22Π态具有较深的势阱,势阱的深度和位置分别为22340.74 cm−1和0.13910 nm.X2Σ+电子组态中一个电子从4σ→5σ的激发产生22Σ+态,22Σ+态也具有较深的势阱,势阱的深度和位置分别为17533.83 cm−1和0.18170 nm.X2Σ+态电子组态中一个电子从1π→2π的激发产生14Σ+,14Δ,14Σ−,12Δ,12Σ−和32Σ+6个态. 其中,32Σ+态具有较浅的势阱,势阱深度为1878.00 cm−1,包含8个振动能级(181.98,509.40,796.10,1044.60,1258.35,1450.13,1633.10和1803.93 cm−1),是一个弱束缚态,同样在Franck-Condon区域是排斥的.其余的5个电子态特征是:1)各自Re处的位置和能量分别密集的分布在0.1600—0.1691 nm和−124.041—−124.024 Hartree的范围内;2)在各自的吸引支分别与22Π态交叉;3)它们到X2Σ+态的跃迁是禁阻的,因此,在实验上很难观察到X2Σ+到这5个态的跃迁.

X2Σ+电子组态中一个电子从4σ→2π的激发产生14Π和32Π态. 14Π势阱的深度和位置分别为584.24 cm−1和0.28487 nm,包含12个振动能级(48.79,139.30,220.32,292.17,355.83,403.70,438.58,475.71,507.06,531.66,551.47和566.60 cm−1),势阱高于离解极限,因此,14Π是不稳定的态.由于32Π与42Π态的避免交叉,从而导致32Π态在核间距R=0.19680 nm处出现势垒,32Π态的势垒和势阱都高于离解极限,并且预解离(将在3.3节讨论)使这个态变得更加不稳定.X2Σ+电子组态中一个电子从1π→6σ和4σ→6σ的激发分别产生排斥态24Π和24Σ+态.

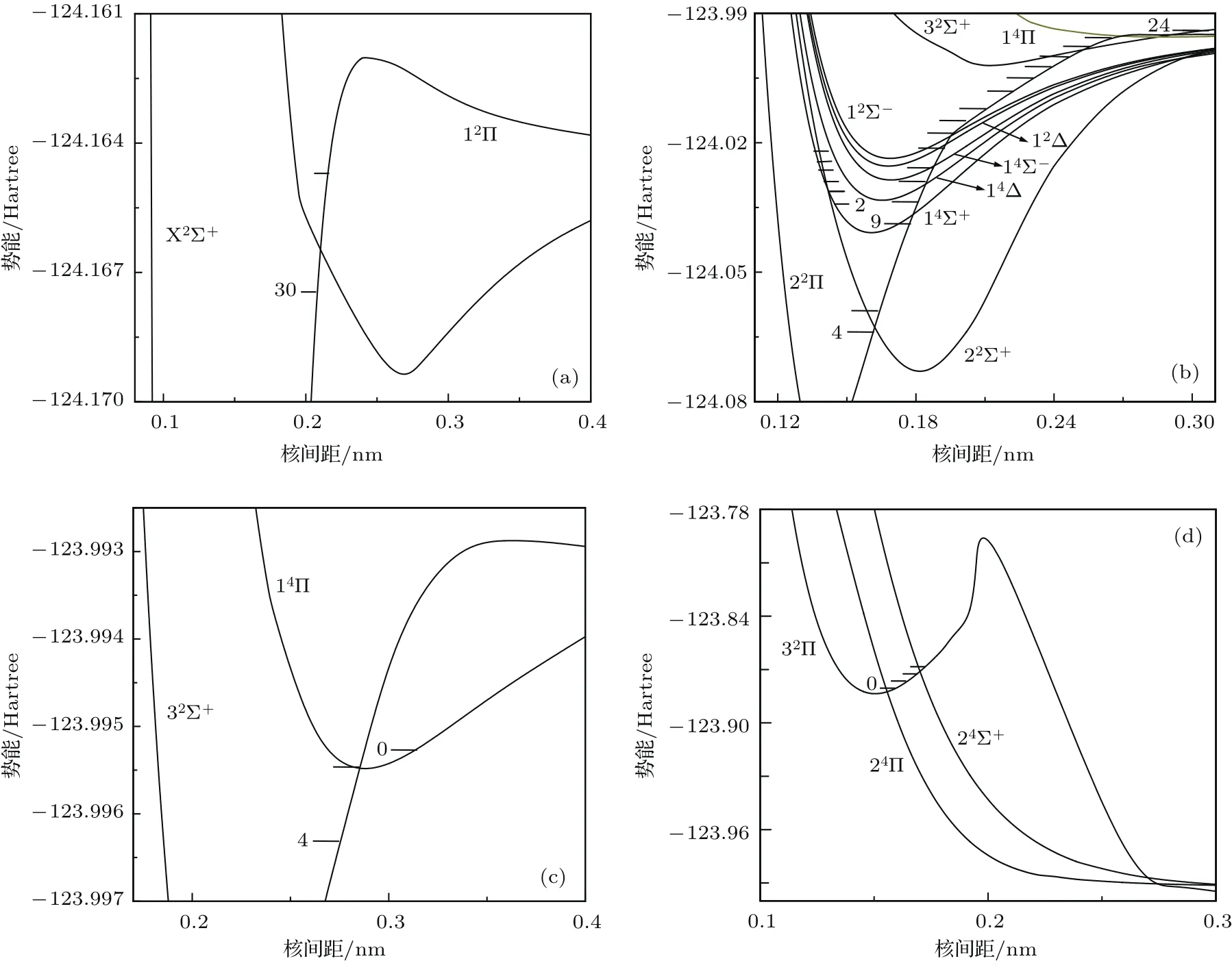
图2 BF+离子PECs交叉区域的放大图以及(a)X2Σ+,(b)22Π和14Σ+,(c)32Σ+和14Π,(d)32Π态所对应的振动能级Fig.2.An enlarged view of crossing regions for PECs of BF+cation and corresponding vibrational levels of the(a)X2Σ+,(b)22Π and 14Σ+,(c)32Σ+and 14Π,and(d)32Π states.

3.3 BF+离子Λ-S态的相互作用

为了讨论BF+离子Λ-S态的PECs交叉和态之间的相互作用,图2给出了PECs交叉区域的放大图连同X2Σ+,22Π,14Σ+,32Σ+和32Π态对应的振动能级.从图2可以看到有三个重要的交叉区域.第一区域位于能量−124.17—−124.16 Hartree范围内,如图2(a)所示,在这个区域,X2Σ+态的PEC与12Π态的PEC交叉.第二区域位于核间距0.12—0.30 nm和能量−124.08—−123.99 Hartree范围内,如图2(b)和图2(c)所示,主要的曲线交叉组成是:22Π态与22Σ+,14Σ+,14Δ,14Σ−,12Δ,12Σ−,32Σ+和14Π态PECs交叉;14Σ+和22Σ+态PECs交叉;32Σ+和 14Π 态PECs交叉.第三区域位于核间距0.10—0.20 nm和能量−123.96—−123.78 Hartree范围内,32Π态分别与24Π和24Σ+态PECs交叉,如图2(d)所示.为了决定这些不同自旋多重性和对称性PECs的耦合强度,本文计算了两个相互作用电子态在曲线交叉区域的旋轨耦合矩阵元,这些旋轨耦合矩阵元的绝对值随核间距的变化如图3所示.

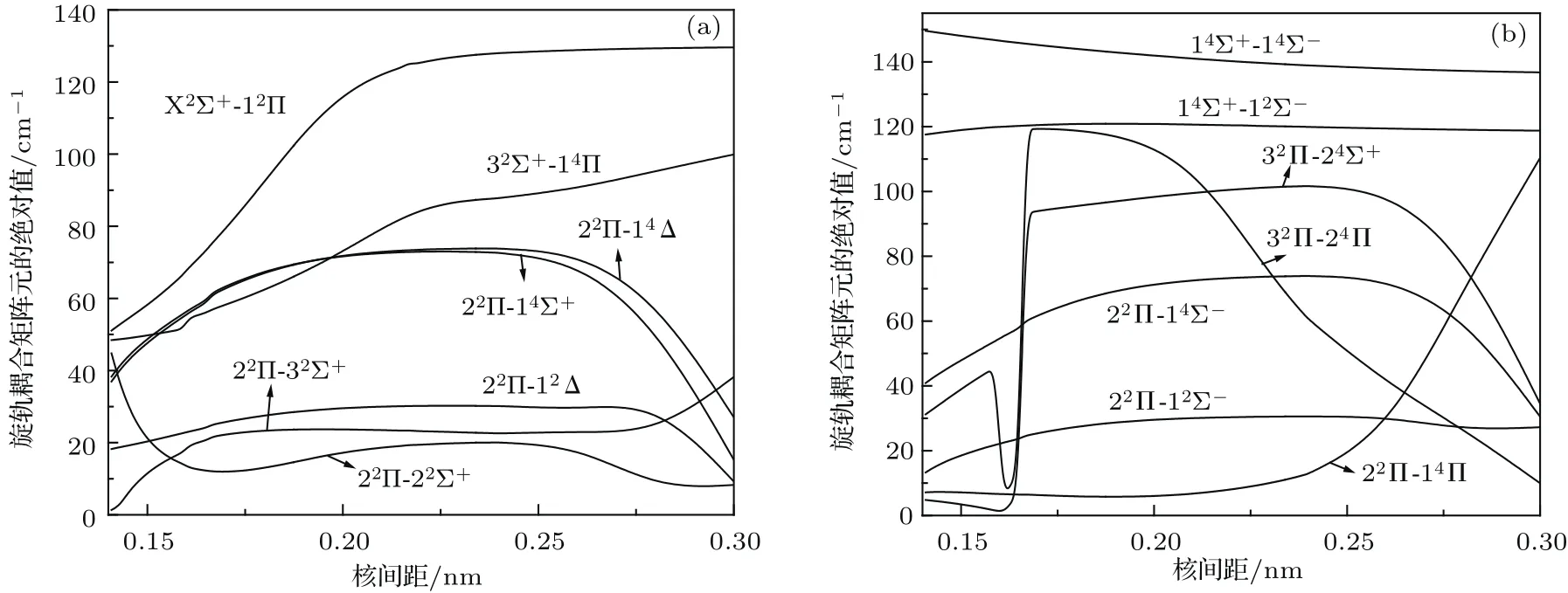
图3 在曲线交叉区域,与(a)X2Σ+,22Π和32Σ+态以及(b)22Π,14Σ+和32Π态相关的旋轨耦合矩阵元的绝对值Fig.3.Evolution of the absolute values of spin-orbit matrix elements related to the(a)X2Σ+,22Π,and 32Σ+states and(b)22Π,14Σ+,and 32Π states in the curve crossing regions.

在第一个曲线交叉区域,X2Σ+态PEC和12Π态PEC的排斥部分相交于R=0.21016 nm,位于X2Σ+态的υ′′=30和υ′′=31振动能级之间.在交叉点,它们之间旋轨耦合矩阵元的绝对值为122.44 cm−1,这为X2Σ+态提供了一个强的预解离通道.

在第二个交叉区域,22Π态与22Σ+,14Σ+,14Δ,14Σ−,12Δ,12Σ−,32Σ+和14Π态 PECs分别在核间距R=0.16209,0.17877,0.18421,0.18795,0.19291,0.19510,0.24760和0.25891 nm处交叉,相应交叉点旋轨耦合矩阵元的绝对值分别为12.63,66.93,68.59,68.88,29.02,29.14,22.58和26.02 cm−1;然而,除了22Π态与22Σ+态的交叉点位于22Σ+态的排斥支外,其他的交叉点位于这些电子态的吸引支,因此预解离通道:22Π(υ′≥ 9)→14Σ+,22Π(υ′≥ 10)→14Δ,22Π(υ′≥ 11)→14Σ−和22Π(υ′≥ 22)→14Π不能打开;但22Π态υ′≥4的振动能级将要被微扰,当υ′≥9时,22Π态与这些态之间的微扰进一步增强.14Σ+PEC和22Σ+PEC在R=0.14165 nm处交叉,位于14Σ+态的υ′=3和υ′=4振动能级之间,但在交叉点处(14Σ+-22Σ+)的旋轨耦合矩阵元的绝对值为0.00 cm−1,因此这个通道是禁阻的;14Δ,14Σ−,12Δ和12Σ−态的势阱位于14Σ+态的内部,其中14Σ+态与14Δ和12Δ态之间不存在相互作用,14Σ−和12Σ−态势阱的底部分别比14Σ+态υ′=4 和υ′=6的能级略高,因此,14Σ+态υ′≥4的振动能级将要被这两个态微扰.另外从图3可以看出,在整个束缚区域,(14Σ+-14Σ−)和 (14Σ+-12Σ−)的旋轨耦合矩阵元的绝对值分别大于115.00和136.00 cm−1,这将增强它们之间的微扰并且增大了检测14Σ+态υ′≥ 4振动能级的困难.32Σ+和14Π态的势阱有重叠部分,交叉点位于32Σ+态的υ′=4和υ′=5振动能级之间,虽然交叉点(R=0.28482 nm)处旋轨耦合矩阵元的绝对值高达95.53 cm−1,但是这个交叉点接近14Π态的势阱,所以预解离通道32Σ+(υ′≥ 4)→14Π不能打开,仅32Σ+态υ′≥ 4的振动能级与14Π态υ′≥0的振动能级存在着强的微扰.

在第三个曲线交叉区域,32Π态与排斥态24Π和24Σ+态PECs分别在核间距R=0.15573和0.17013 nm处交叉.在相应的交叉点处,(32Π-24Π)和(32Π-24Σ+)旋轨耦合矩阵元的绝对值分别为42.76和94.12 cm−1.所以这两个通道32Π(υ′≥ 0)→24Π和32Π(υ′≥ 2)→24Σ+都能导致预解离的产生.因此,旋轨耦合诱导32Π的预解离始于υ′=0的振动能级.

3.4 Ω态的PECs和光谱常数

考虑旋轨耦合效应后,BF+离子14个Λ-S态将产生30个Ω态,包含2个Ω=−1/2态、13个Ω =1/2态、10个Ω =3/2态、4个Ω =5/2态和1个Ω=7/2态.旋轨耦合效应使离解极限B+(1Sg)+F(2Pu)和B+(3Pu)+F(2Pu)分别分裂成2条和6条渐近线,其中B+(1S0)+F(2P3/2)的能量最低.我们把30个Ω态离解极限处的相对能量列入表3.由表3可知,本文计算得到的B+离子3P0-1S0,3P1-1S0,3P2-1S0和F原子2P3/2-2P1/2的能量间隔分别为37434.03,37441.34,37455.95和402.00 cm−1,它们分别与实验值[31,32]37335.54,37341.65,37357.80和404.10 cm−1符合得很好.30个Ω态的PECs见图4.为了使Ω=1/2和Ω=3/2的态能清晰地显示,图4(a)和图4(b)仅给出了核间距0.0808—0.5000 nm范围内的PECs.相应的束缚和准束缚Ω态的光谱常数以及各自Re处主要的Λ-S态权重列于表4.

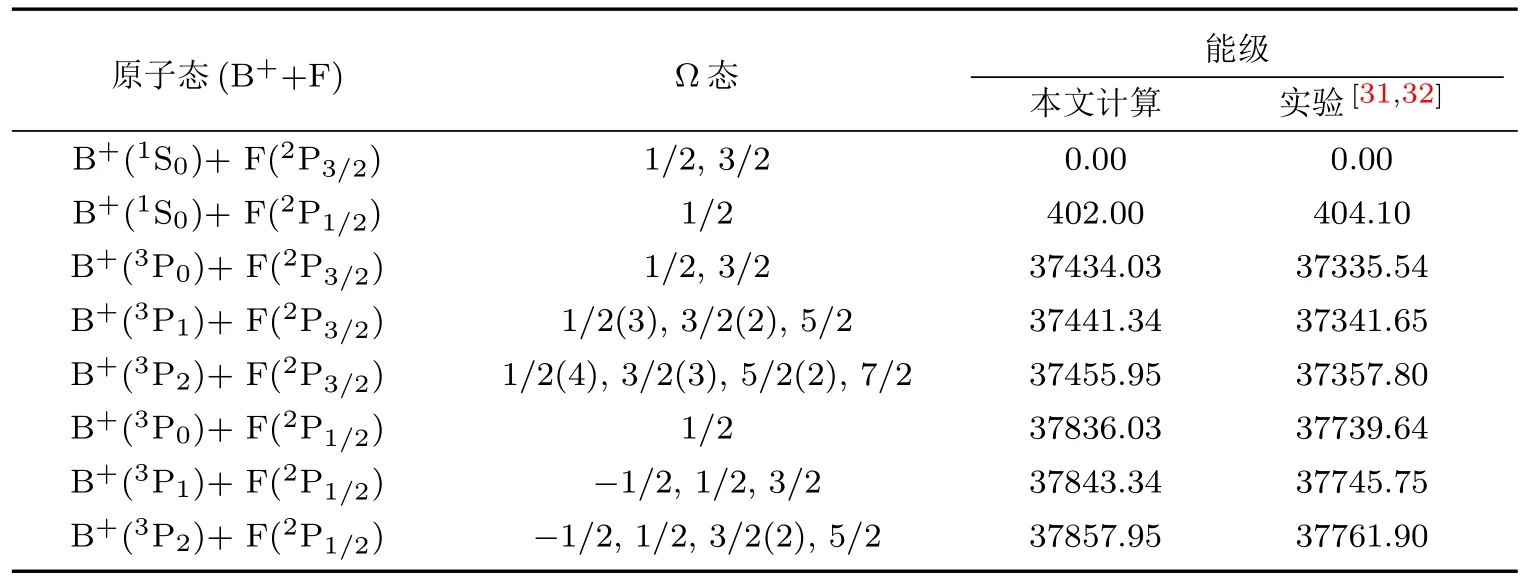
表3 icMRCI+Q/CV+DK+56+SO理论水平上获得的Ω态离解极限处的相对能量Table 3.Relative energies of the Ω states obtained by the icMRCI+Q/CV+DK+56+SO calculations in the dissociation limits.

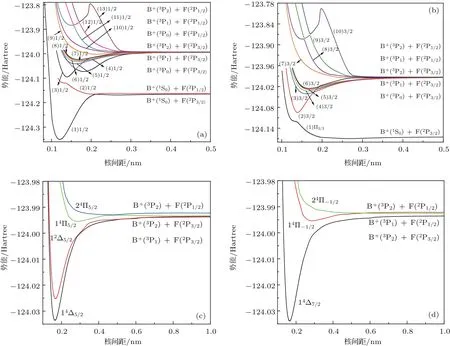
图4 BF+离子30个Ω态的PECs (a)Ω=1/2;(b)Ω=3/2;(c)Ω=5/2;(d)Ω=7/2和Ω=−1/2Fig.4.PECs of 30 Ω states of the BF+cation:(a)Ω=1/2;(b)Ω=3/2;(c)Ω=5/2;(d)Ω=7/2 andΩ=−1/2.

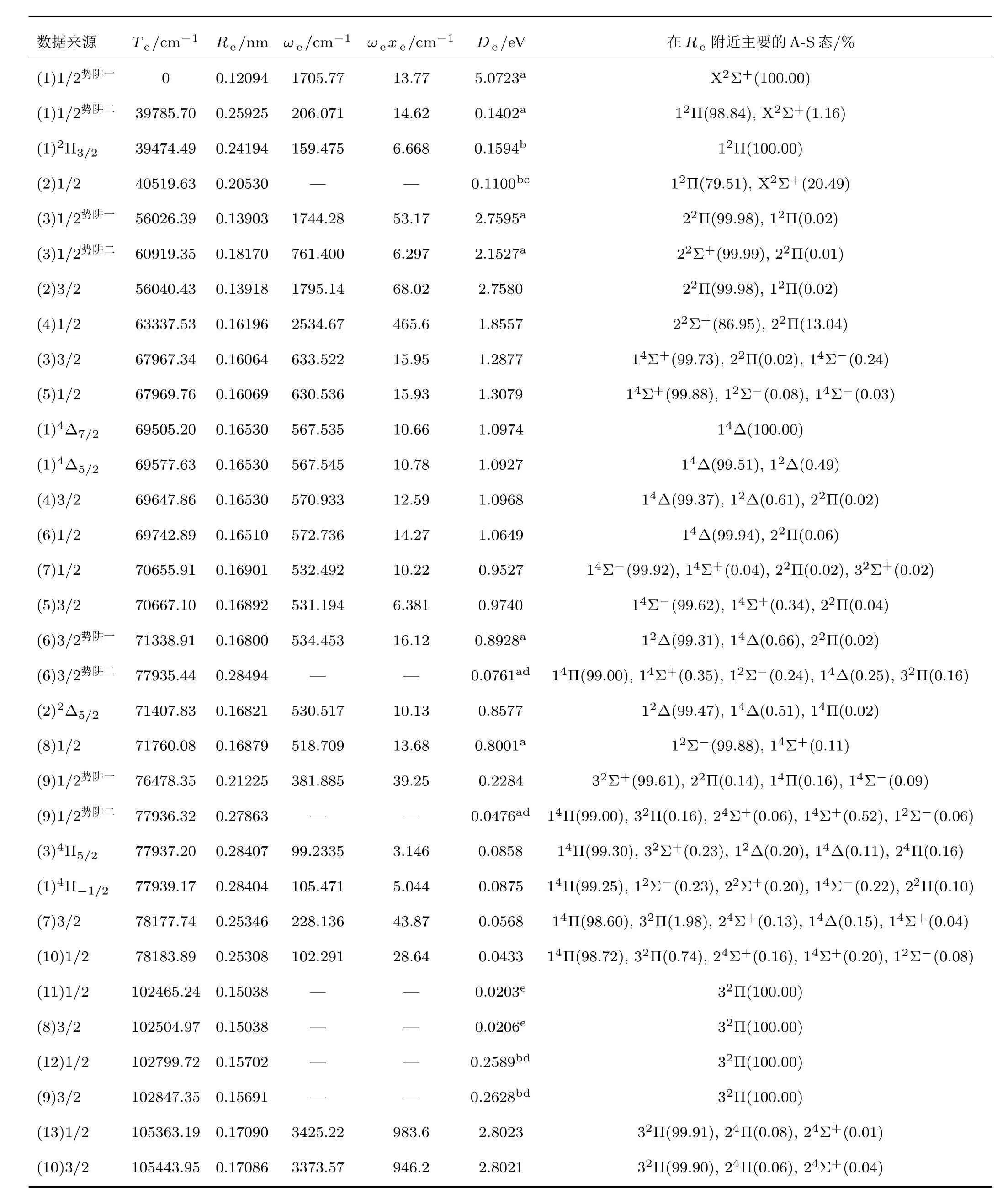
表4 icMRCI+Q/CV+DK+56+SO理论水平上计算的28个束缚和准束缚的Ω态的光谱常数Table 4. Spectroscopic parameters of the 28 bound and quasibound Ω states of BF+cation at level of icMRCI+Q/CV+DK+56+SO.

由3.3节的讨论知,X2Σ+态和12Π态的PECs在核间距R=0.21016 nm处相交,由于具有相同对称性的Ω态之间存在避免交叉规则,因此,X2Σ+分裂出的1个Ω =1/2分量与12Π态所分裂出的1个Ω=1/2分量之间的避免交叉导致:(1)1/2 Ω态具有1个势垒和两个势阱(以下用上标势阱一和势阱二分别表示第一个势阱和第二个势阱);(2)1/2态在Re=0.20530 nm附近出现一局域势阱.对于(1)1/2 Ω态,(1)1/2势阱一主要来自于X2Σ+态,由表1和表4知,它的Re,ωe和ωexe与相应X1Σ+态的差别很小,仅De降低了0.0591 eV,更接近于实验值5.09 eV[5].(1)1/2势阱二主要来自于12Π态,势阱深度为866.05 cm−1,包含8个振动能级(99.26,272.86,408.31,526.29,629.75,719.24,796.05和860.15 cm−1).对于(2)1/2态,势阱的深度为887.12 cm−1,包含2个振动能级(257.99和718.12 cm−1). 12Π Λ-S态分裂出的(1)2Π3/2Ω成分,由于与其他的Ω态之间不存在避免交叉现象,因此(1)2Π3/2Ω态的PEC与12Π Λ-S态的PEC的形状相同.由表1和表4知,其Te,Re,ωe,ωexe和De比相应的12Π Λ-S态分别降低了130.80 cm−1,0.00030 nm,0.324 cm−1,0.498 cm−1和0.0024 eV.

由3.3节的讨论知,22Π态与22Σ+,14Σ+,14Δ,14Σ−,12Δ,12Σ−,32Σ+和14Π态的PECs在核间距0.16—0.26 nm的范围内交叉,因此,22Π分裂出的2个Ω分量(1/2和3/2)与8个Λ-S态(22Σ+,14Σ+,14Δ,14Σ−,12Δ,12Σ−,32Σ+和14Π)分裂出的17个Ω分量(1个−1/2,7个1/2,5个3/2,3个5/2和1个7/2)之间存在12个避免交叉点;同理,32Π态分裂出的2个Ω分量(1/2和3/2)与24Π和24Σ+态所分裂出的6个Ω分量(1个−1/2,2个1/2,2个3/2和1个5/2)之间存在4个避免交叉点;另外,22Σ+分裂出的1个Ω=1/2的态与14Σ+态分裂出的Ω=1/2的态之间存在1个避免交叉点;32Σ+分裂出的1个Ω =1/2的态与14Π态分裂出的Ω=1/2的态之间存在1个避免交叉点.并且在避免交叉点附近,Ω态的ΛS成分有显著的变化并且将形成一些局域势阱,所以,这些Ω态的PECs的形状与相应的Λ-S态的PECs的形状明显的不同.其中,(2)3/2,(4)1/2,(3)3/2,(5)1/2,(4)3/2,(6)1/2,(7)1/2,(5)3/2,(8)1/2,(7)3/2,(10)1/2,(11)1/2,(8)3/2,(12)1/2,(9)3/2,(12)1/2,(13)1/2和(10)3/2这18个Ω态具有单势阱;(3)1/2,(6)3/2和(9)1/2这3个Ω态具有双势阱.

首先讨论18个单势阱Ω态,对于(2)3/2 Ω态,其主要的Λ-S成分从R=0.13918 nm处的22Π (99.98%)变化到R=0.17880 nm处的14Σ+(97.98%),其势阱深度为22245.73 cm−1,包含36个振动能级. 对于(4)1/2 Ω态,其主要的Λ-S成分从R=0.14080 nm处的14Σ+(99.94%)变化到R=0.16196 nm处的22Σ+(86.95%)又变化到R=0.16480 nm处的22Π(99.91%)再变化到R=0.17880 nm处的14Σ+(99.17%),其势阱深度为14967.29 cm−1,包含33个振动能级.对于(3)3/2 Ω态,其主要的Λ-S成分从R=0.15080 nm处的14Σ+(99.84%)变化到R=0.17880 nm处的22Π(96.50%)再变化到R=0.18480 nm处的14Δ (97.35%),其势阱深度为10386.42 cm−1,包含33个振动能级.对于(5)1/2 Ω态,其主要的Λ-S成分从R=0.14080 nm处的22Σ+(99.97%)变化到R=0.16069 nm处的14Σ+(99.88%)再变化到R=0.17880 nm处的22Π (96.18%)以及变化到R=0.18480 nm处的14Δ (89.78%),其势阱深度为10549.05 cm−1,包含33个振动能级. 对于(4)3/2 Ω态,其主要的Λ-S成分从R=0.16530 nm处的14Δ (99.37%)变化到R=0.18480 nm处的22Π (77.51%)再变化到R=0.18880 nm处的14Σ−(95.95%),其势阱深度为8823.76 cm−1,包含33个振动能级.对于(6)1/2 Ω态,其主要的Λ-S成分从R=0.16510 nm处的14Δ (99.94%)变化到R=0.18480 nm处的22Π(74.34%)再变化到R=0.18880 nm处的14Σ−(98.82%),其势阱深度为8589.36 cm−1,包含30个振动能级.对于(7)1/2 Ω态,其主要的Λ-S成分从R=0.16901 nm处的14Σ−(99.92%)变化到R=0.18880 nm处的22Π(78.76%)再变化到R=0.19680 nm处的12Σ−(98.02%),其势阱深度为7684.03 cm−1,包含32个振动能级.对于(5)3/2 Ω态,其主要的Λ-S成分从R=0.16892 nm处的14Σ−(99.62%)变化到R=0.18880 nm处的22Π(96.49%)再变化到R=0.19480 nm处的12Δ (98.04%),其势阱深度为7856.31 cm−1,包含30个振动能级.对于(8)1/2 Ω态,其主要的ΛS成分从R=0.16879 nm处的12Σ−(99.88%)变化到R=0.19680 nm处的22Π(98.66%)又变化到R=0.24080 nm处的32Σ+(98.30%)再变化到R=0.30080 nm处的14Π(98.17%),其势阱深度为6453.65 cm−1,包含16个振动能级.对于(7)3/2Ω态,其主要的Λ-S成分从R=0.25346 nm处的14Π (98.60%)变化到R=0.26080 nm处的22Π(98.60%),其势阱深度为457.82 cm−1,包含6个振动能级(121.33,340.96,381.79,404.49,426.95和445.12 cm−1). 对于(10)1/2 Ω态,其主要的Λ-S成分从R=0.25308 nm处的14Π (98.72%)变化到R=0.26080 nm处的22Π(97.29%),其势阱深度为349.18 cm−1,包含7个振动能级(56.48,168.66,206.88,254.17,306.70,315.87和348.86 cm−1).对于(11)1/2 Ω 态,其主要的Λ-S成分从R=0.15038 nm处的32Π(100.00%)变化到R=0.15680 nm处的24Π(100.00%),其势阱深度为163.95 cm−1,不包含任何振动态.对于(8)3/2 Ω态,其主要的Λ-S成分从R=0.15038 nm处的32Π (100.00%)变化到R=0.15680 nm处的24Π (99.99%),其势阱深度为165.92 cm−1,不包含任何振动态.对于(12)1/2 Ω态,其主要的Λ-S成分从R=0.15480 nm处的24Π(100.00%)变化到R=0.15702 nm处的32Π (100.00%)再变化到R=0.17280 nm处的24Σ+(99.98%),其势阱深度为2087.86 cm−1,包含1个振动能级(1132.28 cm−1). 对于(9)3/2 Ω态,其主要的ΛS成分从R=0.15480 nm处的24Π (100.00%)变化到R=0.15691 nm处的32Π (100.00%)再变化到R=0.17280 nm处的24Σ+(99.96%),其势阱深度为2119.25 cm−1,包含1个振动能级(1109.07 cm−1). 对于(13)1/2 Ω态,其主要的Λ-S成分从R=0.16880 nm处的24Σ+(99.98%)变化到R=0.17090 nm处的32Π(99.91%),其势阱深度为22602.16 cm−1,包含12个振动能级(1489.77,3547.47,5298.77,6832.28,8424.69,10157.36,11939.24,13798.02,15690.30,17618.59,19562.35和21524.35 cm−1). 对于(10)3/2 Ω态,其主要的Λ-S成分从R= 0.16880 nm处的24Σ+(99.97%)变化到R=0.17086 nm处的32Π(99.90%),其势阱深度为22600.40 cm−1,包含12个振动能级(1472.28,3526.49,5275.00,6808.52,8397.05,10124.78,11905.47,13760.53,15651.24,17577.31,19519.75和21480.13 cm−1).

下面讨论3个具有双势阱的Ω态,对于(3)1/2 Ω态,其主要的Λ-S成分从R=0.13903 nm处的22Π(99.98%)变化到R=0.18170 nm处的22Σ+(99.99%),其中(3)1/2势阱一态的势阱深度为6985.44 cm−1,包含5个振动能级(858.59,2489.92,3996.58,5403.82和6703.55 cm−1);(3)1/2势阱二的势阱深度为2092.47 cm−1,包含3个振动能级(378.92,1122.43和1838.69 cm−1). 对于(6)3/2 Ω态,其主要的Λ-S成分从R=0.16800 nm处的12Δ (99.31%)变化到R=0.19480 nm处的22Π (99.20%)再变化到R=0.28494 nm处的14Π (99.00),其中(6)3/2势阱一态的势阱深度为6680.59 cm−1,包含14个振动能级(263.69,778.77,1297.25, 1849.45, 2442.28, 3040.35, 3597.82,4130.97, 4631.09, 5090.01, 5508.23, 5887.96,6224.92和6529.51 cm−1);(6)3/2势阱二的势阱深度为84.06 cm−1,包含1个振动能级(51.80 cm−1).对于(9)1/2 Ω态,其主要的Λ-S成分从R=0.21225 nm处 的32Σ+(99.61%)变 化 到R=0.27863 nm处的14Π (99.00%)再变化到R=0.28080 nm处的32Σ+(53.49),其中(9)1/2势阱一态的势阱深度为1545.54 cm−1,包含5个振动能级(182.01,508.38,819.87,1129.99和1433.73 cm−1);(9)1/2势阱二的势阱深度为87.57 cm−1,包含1个振动能级(76.12 cm−1).

14Δ Λ-S态分裂出的(1)4Δ7/2和(1)4Δ5/2Ω成分,12Δ Λ-S态分裂出的(2)2Δ5/2Ω成分,14Π Λ-S态分裂出的(3)4Π5/2和(1)4Π−1/2Ω成分以及24Π Λ-S态分裂出的(4)4Π5/2和(2)4Π−1/2Ω成分. 由于与其他的Ω态之间不存在避免交叉现象,因此这7个 Ω态的PECs与相应的Λ-S态的PECs的形状相同. 由表1和表4知,(1)4Δ7/2态和(1)4Δ5/2的Te分别比相应的14Δ Λ-S态降低了117.42 cm−1和44.99 cm−1,然而它们的Re,ωe和ωexe比相应的14Δ Λ-S态分别增大了0.00001 nm,1.802 cm−1和1.35 cm−1及0.00001 nm,1.812 cm−1和1.47 cm−1;另外,(1)4Δ7/2态 的De比 相 应 的14Δ Λ-S态 增 大 了0.0001 eV,(1)4Δ5/2态的De比相应的14Δ Λ-S态减小了0.0046 eV.(2)2Δ5/2态的Te,Re和ωe分别比相应的12Δ Λ-S态增大了44.34 cm−1,0.00020 nm和0.524 cm−1;ωexe和De分别比相应的12Δ Λ-S态减小了0.20 cm−1和0.0218 eV.(3)4Π5/2和(1)4Π−1/2的Te和De分别比相应的14Π Λ-S态 增 大 了16.02 cm−1和0.0134 eV及17.99 cm−1和0.0151 eV;然而它们的Re分别比相应的14Π Λ-S态减小了0.00080 nm和0.00083 nm,另外,(3)4Π5/2态的ωe和ωexe比相应的14Π ΛS态减少了0.7027 cm−1和1.556 cm−1;(1)4Π−1/2态 的ωe和ωexe比 相 应 的14Π Λ-S态 增 大 了5.5348 cm−1和0.342 cm−1.(4)4Π5/2和(2)4Π−1/2这2个Ω态仍然是排斥态.

3.5 跃迁特性

为了研究22Π—X2Σ+和22Σ+—X2Σ+的跃迁特性,我们在icMRCI/AV6Z理论水平上计算了这两对跃迁的跃迁偶极距(TDMs),并把TDMs曲线(TDMCs)绘于图5中.由图5可以看出,当核间距R＞0.30 nm,这两对跃迁的TDMs趋近于零渐近线;另外,22Π—X2Σ+和22Σ+—X2Σ+的TDMs分别在核间距R=0.1408 nm和R=0.1888 nm附近出现极大值,这有利于它们之间的跃迁,然而,由3.3节的讨论知,22Π态υ′≥ 9的振动能级(对应核间距为R≤0.12004 nm和R≥0.17768 nm)将受到其他态强的微扰,这将不利于实验上观察22Π态υ′≥9的振动能级.

基于icMRCI+Q/CV+DK+56计算获得的22Π, 22Σ+和X2Σ+态 的PECs以 及icMRCI/AV6Z计算获得的22Π—X2Σ+和22Σ+—X2Σ+的TDMs,利用LEVEL 8.0程序[28]获得了这两对跃迁的Franck-Condon因子(qυ′,υ′′)和爱因斯坦自发辐射系数(Aυ′,υ′′), 由于篇幅的限制, 我们将其列入附录A表A1和A2.由表A1和A2可知,随着υ′或υ′′的变化, 这两对跃迁的qυ′,υ′′和Aυ′,υ′′数量级的变化趋势无规律性,另外,对于一个确定的υ′,随着υ′′的变化,一些相对大的qυ′,υ′′对应着相对大的Aυ′,υ′′(数量级在105—106s−1范围内),这将有利于22Π和22Σ+态的实验观察;然而,对于22Σ+—X2Σ+ 跃迁,相对大的qυ′,υ′′和Aυ′,υ′′对应于X2Σ+态高振动能级,这增加了实验上观察22Σ+态的困难.

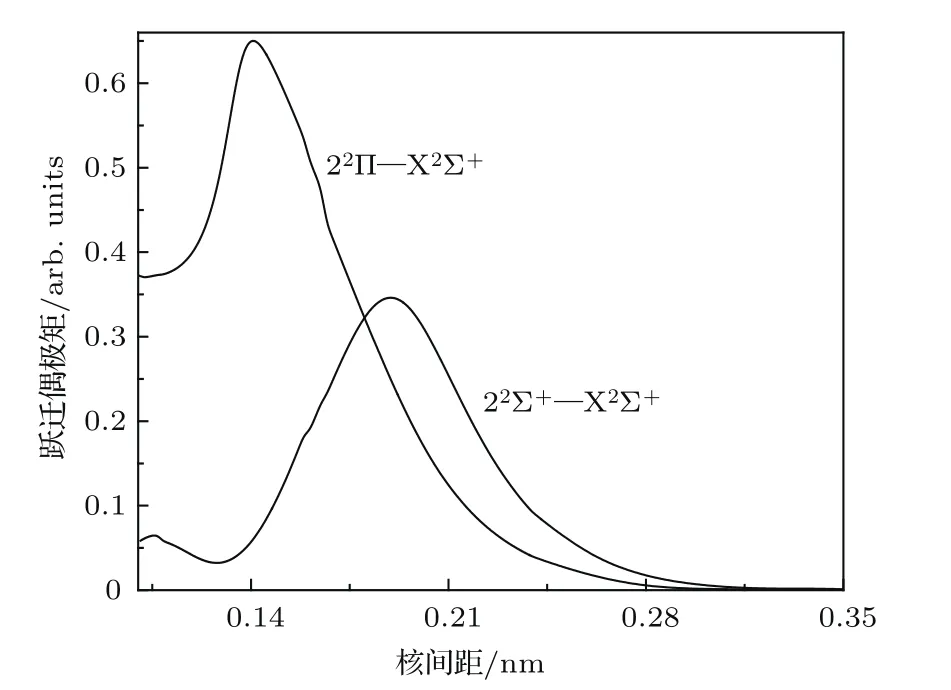
图5 BF+离子22Π—X2Σ+和22Σ+—X2Σ+的TDMCsFig.5.TDMCs ofthe 22Π–X2Σ+and 22Σ+–X2Σ+transitions of BF+cation.

上态一个υ′能级的辐射寿命(τυ′)等于υ′能级到下态所有υ′′能级的Aυ′,υ′′和的倒数[33]. 因此,对于给定激发态υ′能级的τυ′可以通过下面的公式获得:

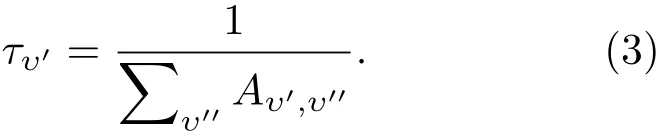
根 据(3)式, 本 文 得 到 了22Π(υ′= 0—9)和22Σ+(υ′=0—2)到X2Σ+态跃迁的τυ′,并把它们列入表5.

表5 BF+ 离子22Π (υ′=0—9)和22Σ+(υ′=0—2)到X2Σ+ 态跃迁的τυ′(ns)Table 5. τυ′(ns)values of the transitions from the 22Π (υ′=0–9)and 22Σ+(υ′=0–2)excited states to the X2Σ+state for BF+cation.

如表5所示,本文计算的22Π (υ′=0—9)—X2Σ+和22Σ+(υ′=0—2)—X2Σ+跃迁的τυ′依赖于振动能级. 随着υ′的增大,22Π (υ′=0—9)—X2Σ+和22Σ+(υ′=0—2)—X2Σ+跃迁的τυ′逐渐增大.

考虑旋轨耦合效应后,由3.4节的讨论知,(1)1/2势阱一, (3)1/2势阱一, (3)1/2势阱二和(2)3/2(υ′=0—9)Ω态主要的Λ-S成分分别为X2Σ+,22Π,22Σ+和22Π态. 基于icMRCI+Q/CV+DK+56+SO计 算 的(3)1/2势阱一, (2)3/2,(3)1/2势阱二和(1)1/2势阱一Ω态 的PECs以 及icMRCI/AV6Z计算获得的(3)1/2势阱一— (1)1/2势阱一,(2)3/2—(1)1/2势阱一和 (3)1/2势阱二—(1)1/2势阱一的TDMs,利用LEVEL 8.0程序[28]获得了这三 对 跃 迁 的qυ′,υ′′和Aυ′,υ′′, 并 把 它 们 列 入 附录A中的表A2—A4.同样根据(3)式,计算得到(3)1/2势阱一(υ′= 0—4)—(1)1/2势阱一,(2)3/2(υ′=0—9)—(1)1/2势阱一和(3)1/2势阱二(υ′=0—2)—(1)1/2势阱一跃迁的τυ′,并把它们列入附录A表A5.通过对表A1—A4的比较可知,旋轨耦合效应总体上对 本文所涉及跃迁相应的qυ′,υ′′的影响不大;然而,对跃迁概率相对大(数量级在105—107s−1)的波带, 除了(3)1/2势阱一(υ′=0—4)—(1)1/2势阱一的跃迁概率略高于22Π (υ′=0—4)—X2Σ+跃迁概率的两倍,其他两对Ω态跃迁的跃迁概率或稍低、或等于、或稍高于相应Λ-S态跃迁的跃迁概率.另外,通过对表5和表A5的比较可知,(3)1/2势阱一(υ′=0—4)—(1)1/2势阱一的τυ′约为22Π (υ′=0—4)—X2Σ+的τυ′的1/2,(2)3/2(υ′= 0—9)—(1)1/2势阱一和(3)1/2势阱二(υ′=0—2)—(1)1/2势阱一跃迁的τυ′比相应Λ-S态跃迁的τυ′略大.

4 结 论

本文利用icMRCI+Q方法在核间距为0.0808—1.0608 nm内计算了BF分子X1Σ+态和BF+离子14个Λ-S态的PECs,并在计算中纳入旋轨耦合效应获得BF+离子14个Λ-S态所产生的30个Ω态的PECs.使用态相互作用方法、非收缩全电子CVTZ基组和完全SO处理旋轨耦合效应,并对所有的PECs进行了核价相关、标量相对论修正以及外推至完全基组极限.基于得到的PECs,分别获得了BF分子X1Σ+态的VIPs和AIPs,BF+离子束缚和准束缚的12个Λ-S态和28个Ω态的光谱常数,并且BF+(X2Σ+)←BF(X1Σ+)的VIP和AIP以及BF+离子X2Σ+态的光谱常数与已有的实验结果符合.这表明了本文报道的BF的X1Σ+态到BF+离子12Π和22Σ+态的电离势、BF+离子其他11个Λ-S态以及28个Ω态的光谱常数也应是可靠的. 计算结果表明X2Σ+,22Π,14Σ+,32Σ+和32Π态与其他的激发电子态的PECs进行交叉,借助于计算的旋轨耦合矩阵元,分析了X2Σ+和32Π态的预解离机理:旋轨耦合效应诱导X2Σ+和32Π态预解离的产生,其预解离分别开始于υ′′=30和υ′=0的振动能级;研究了22Π,14Σ+,32Σ+与其他激发电子态的相互作用,22Π(υ′≥ 9),14Σ+(υ′≥ 4)和32Σ+(υ′≥ 4)的振动能级将要受到强的微扰.计算了30个Ω态的离解极限处的相对能量,并且与实验结果十分符合. 最后,计算了22Π(υ′=0—9)—X2Σ+,22Σ+(υ′= 0—2)—X2Σ+,(3)1/2—(1)1/2势阱一和(2)3/2(υ′=0—9)—(1)1/2势阱一跃迁的qυ′,υ′′,Aυ′,υ′′和τυ′. 我们期待本文的研究结果能激起实验和理论物理学家对BF+离子旋轨耦合效应、预解离机理和跃迁特性进一步研究的兴趣.

附录A 22Π—X2Σ+,22Σ+—X2Σ+,(3)1/2—(1)1/2势阱一和(2)3/2—(1)1/2势阱一的跃迁特性

表A1 22Π(υ′=0—9)—X2Σ+ 跃迁的qυ′,υ′′(第一行) 和Aυ′,υ′′(s−1,第二行)Table A1.qυ′,υ′′ (1st line)and Aυ′,υ′′(s−1,2nd line)values for the 22Π (υ′=0–9)–X2Σ+transitions.

表A2 22Σ+(υ′=0—2)—X2Σ+ 和(3)1/2势阱二—(1)1/2势阱一 跃迁的qυ′,υ′′ (第一行)和Aυ′,υ′′(s−1,第二行)Table A2.qυ′,υ′′ (1st line)and Aυ′,υ′′ (s−1,2nd line)values for the 22Σ+(υ′=0–2)–X2Σ+and(3)1/22ndwell–(1)1/21stwelltransitions.

表A3 (3)1/2势阱一—(1)1/2势阱一 跃迁的qυ′,υ′′(第一行)和Aυ′,υ′′(s−1,第二行)Table A3.qυ′,υ′′(1st line)and Aυ′,υ′′(s−1,2nd line)values for the(3)1/21stwell–(1)1/21stwelltransition.

表A4 (2)3/2(υ′=0—9)—(1)1/2势阱一 跃迁的qυ′,υ′′(第一行)和Aυ′,υ′′(s−1,第二行)Table A4.qυ′,υ′′(1st line)and Aυ′,υ′′ (s−1,2nd line)values for the(2)3/2(υ′=0–9)–(1)1/21stwelltransition.

表A5 BF+离子(3)1/2和(2)3/2(υ′=0—9)到(1)1/2势阱一态跃迁的τυ′(ns)Table A5. τυ′(ns)values of the transitions from the(3)1/2 and(2)3/2(υ′=0–9) Ω states to the(1)1/21stwellΩstate for BF+cation.

[1]Chakrabarti K,Tennyson J 2009J.Phys.B:At.Mol.Opt.Phys.42 105204

[2]Hildenbrand D L 1971Int.J.Mass Spectrom.Ion Phys.7 255

[3]Robinson D W 1963J.Mol.Spectrosc.11 275

[4]Caton R B,Douglas A E 1970Can.J.Phys.48 432

[5]Dyke J M,Kirby C,Morris A 1983J.Chem.Soc.,Faraday Trans.279 483

[6]Winifred M H 1965J.Chem.Phys.43 624

[7]Nesbet R K 1965J.Chem.Phys.43 4403

[8]Cade P E,Huo W M 1975At.Data Nucl.Data Tables15 1

[9]Rosmus P,Werner H J,Grimm M 1982Chem.Phys.Lett.92 250

[10]Bauschlicher C W,Ricca A 1999J.Phys.Chem.A103 4313

[11]Bruna P J,Grein F 2001J.Phys.Chem.A105 3328

[12]Magoulas I,Kalemos A,Mavridis A 2013J.Chem.Phys.138 104312

[13]Niu X H,Shu H B,Zhu Z L,Chen Q 2016Spectrochim.Acta A159 60

[14]Li R,Wei C L,Sun Q X,Sun E P,Jin M X,Xu H F,Yan B 2013Chin.Phys.B22 123103

[15]Li R,Zhang X M,Jin M X,Xu H F,Yan B 2014Chin.Phys.B23 053101

[16]Xing W,Liu H,Shi D H,Sun J F,Zhu Z L,Lü S X 2015Acta Phys.Sin.64 153101(in Chinese)[邢伟,刘慧,施德恒,孙金峰,朱遵略,吕淑霞2015物理学报64 153101]

[17]Liu X J,Miao F J,Li R,Zhang C H,Li Q N,Yan B 2015Acta Phys.Sin.64 123101(in Chinese)[刘晓军,苗凤娟,李瑞,张存华,李奇楠,闫冰2015物理学报64 123101]

[18]Zhao S T,Liang G Y,Li R,Li Q N,Zhang Z G,Yan B 2017Acta Phys.Sin.66 063103(in Chinese)[赵书涛,梁桂颖,李瑞,李奇楠,张志国,闫冰2017物理学报66 063103]

[19]Werner H J,Knowles P J,Lindh R,Manby F R,Schütz M,Celani P,Korona T,Mitrushenkov A,Rauhut G,Adler T B,Amos R D,Bernhardsson A,Berning A,Cooper D L,Deegan M J O,Dobbyn A J,Eckert F,Goll E,Hampel C,Hetzer G,Hrenar T,Knizia G,Köppl C,Liu Y,Lloyd A W,Mata R A,May A J,McNicholas S J,Meyer W,Mura M E,Nicklass A,Palmieri P,P fl üger K,Pitzer R,Reiher M,Schumann U,Stoll H,Stone A J,Tarroni R,Thorsteinsson T,Wang M,Wolf A 2010MOLPRO:a package of ab initio programs,http://www.molpro.net

[20]LanghoffS R,Davidson E R 1974Int.J.Quantum Chem.8 61

[21]Richartz A,Buenker R J 1978Chem.Phys.28 305

[22]Wilson A K,van Mourik T,Dunning T H 1996J.Mol.Struct.(Theochem)388 339

[23]Dunning T H 1989J.Chem.Phys.90 1007

[24]Woon D E,Dunning T H 1995J.Chem.Phys.103 4572[25]Reiher M,Wolf A 2004J.Chem.Phys.121 2037

[26]Wolf A,Reiher M,Hess B A 2002J.Chem.Phys.117 9215

[27]Oyeyemi V B,KrisiloffD B,Keith J A,Libisch F,Pavone M,Carter E A 2014J.Chem.Phys.140 044317[28]Le Roy R J 2007LEVEL 8.0:A Computer Program for Solving the Radial Schrödinger Equation for Bound and Quasibound Levels(Waterloo:University of Waterloo Chemical Physics Research Report)CP-663

[29]Kramida A E,Ryabtsev A N 2007Phys.Scr.76 544

[30]Lidén K 1949Ark.Fys.1 229

[31]Ryabtsev A N,Kink I,Awaya Y,Ekberg J O,Mannervik S,Ölme A,Martinson I 2005Phys.Scr.71 489

[32]Moore C E 1971Atomic Energy Levels(Vol.1)(Washington,DC:National Bureau of Standard)p60

[33]Okabe H(translated by Tang G Q,Bai Y B,Lu Z G)1982Photochemistry of Small Molecules(Changchun:Jilin People’s Press)p40(in Chinese)[冈田秀雄 著 (汤国庆,白玉白,陆志刚 译)1982小分子光化学(长春:吉林人民出版社)第40页]