相位调制激光多普勒频移测量方法的改进∗

杜军 杨娜 李峻灵 曲彦臣 李世明 丁云鸿 李锐

1)(哈尔滨师范大学计算机科学与信息工程学院,哈尔滨 150052)

2)(黑龙江工程学院电气与信息工程学院,哈尔滨 150050)

3)(哈尔滨工业大学,可调谐激光技术国家级重点实验室,哈尔滨 150080)

1 引 言

激光多普勒频移测量方法可以用于获取目标的振动和速度等信息[1−3].由于其具有极高的时-空分辨,所以一直以来备受关注,并在很多领域中得以应用,例如:军事伪装目标识别、全球大气风场测量等[4,5].按照工作原理,通常激光多普勒频移测量方法可以分成两类:相干(外差)探测方法和直接(非相干)探测方法.虽然这两种方法都有各自的优势,但也都存在明显的不足.相干探测方法是利用信号光和本振光产生的拍频信号来进行多普勒频移测量[6−12].由于本振光对信号光的转换增益作用以及滤波作用,理论上相干探测方法可以具有极高的测量精度.但由于信号光与本振光所经过的路径不同,所以为了保证它们的孔径、传播方向以及波前等相匹配以获得较高的拍频效率,将会给光学系统及其装调带来极高的要求.另外,由于信号光与本振光通常不是源于光源同一时刻出射的光,为了保证其相干性,需要光源具有极窄的带宽和极高的频率稳定性.所以,相干探测方法对光学系统和光源的要求极其苛刻,难以实现.直接探测是利用出射光与回波信号光通过边缘滤波器的相对能量变化来进行多普勒频移测量.由于基于Fabry-Perot(F-P)干涉仪的边缘技术方法结构简单、安全可靠、方便灵活,是主要的直接探测方法[13−16].虽然该方法对光源和光学系统要求不高,容易实现,但由于其探测器输出信号为基带信号,且工作带宽较大,所以进入系统的噪声功率较大,在没有有效方法抑制噪声的情况下,测量精度较低.

正是基于上述原因,相位调制多普勒频移测量方法得以提出[17−19].这种方法能够兼具直接探测方法和相干探测方法的优势.经过正弦相位调制的信号光,可以在其原有频率成分(载波)的基础上产生振幅相等、相位相反的正、负一阶边带,当利用F-P干涉仪调整载波与边带的振幅和相位,将会破坏其对称性,并产生固定频率的拍频信号.相位调制多普勒频移方法就是利用此拍频信号的振幅(或相位)随信号光频率变化的性质来进行多普勒频移测量.由于产生此拍频信号的光波是同一信号光的不同频率成分,所以具有相同的孔径、传播方向、偏振以及波前,并且相干性也不会随探测距离的增加而降低.这就使得相位调制多普勒频移测量方法对光源和光学系统的要求较低,易于实现.利用相关检测等方法对相位调制拍频信号的振幅(或相位)进行提取,可以有效地降低系统的工作带宽,从而减小进入的噪声功率,这就使得相位调制多普勒频移测量方法可以具有极高的测量精度.

然而,由于目前对相位调制多普勒频移测量方法的研究还不够深入,所以很多方面还存在不足,有待提高.例如:由于需要额外的探测器对信号光的光强进行检测,使其系统结构较复杂且造价较高;相位调制信号直流分量中也包含大量的有用信息,但却没能够得到有效的利用,造成信息的浪费等.本文旨在对现有相位调制多普勒频移测量方法进行改进,使其可以充分地利用相位调制信号中的有用信息来弥补自身的不足,并能够进一步提升自身的性能.

2 理论研究

2.1 相位调制基本原理

在经过正弦相位调制后的单频信号光可以表示为

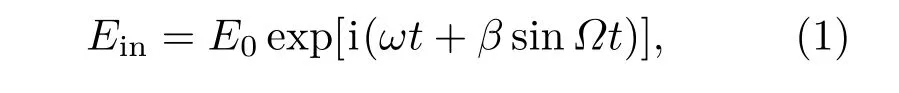
其中,E0和ω分别是信号光的场强和角频率;Ω和β分别是正弦相位调制角频率和调制度.

利用贝塞尔函数可将(1)式展开成载波(ω)和边带(ω±nΩ, 阶数n=1,2,3,···)相叠加的形式[20].当调制度β＜0.9时,二阶边带与载波的振幅比小于1.4%,所以可将二阶以上边带忽略,这样(1)式可以表示为

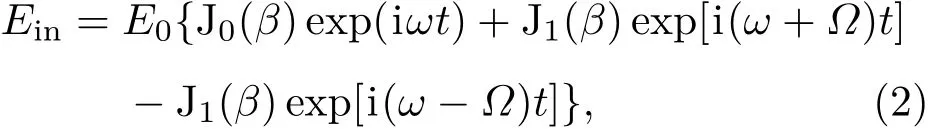
其中,J0和J1分别是零阶和一阶贝塞尔函数.

(2)式中的第一项为信号光原有频率成分(载波),第二和第三项分别为振幅相等、相位相反的正、负一阶边带.令此调制信号光通过F-P干涉仪,并利用光电探测器进行测量,输出的电信号可以表示为

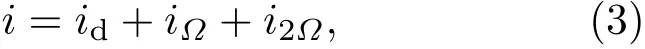
其中,id为直流信号;iΩ为一倍调制频率Ω拍频信号(由载波和两个一阶边带产生);i2Ω为二倍调制频率2Ω拍频信号(由正、负一阶边带产生,由于强度较弱,本文不予考虑).

直流信号id可以由下式表示为[20]:

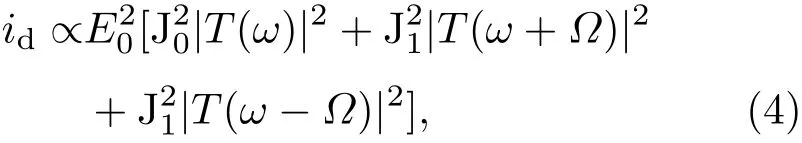
其中,T为F-P干涉仪场强透过系数.

由于(4)式中F-P干涉仪场强透过系数T的模方为光强透过率h,即h=|T|2,所以(4)式中的括号部分可以等效成调制信号光(载波与边带)的F-P干涉仪光强透过率.如果由h′代替,即h′(ω)=J20|T(ω)|2+J21|T(ω+Ω)|2+J21|T(ω−Ω)|2,那么(4)式变为

一倍调制频率拍频信号iΩ可以表示为[20]:

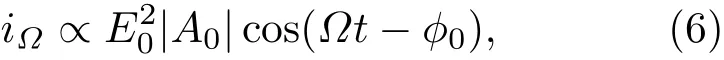
其中,

通过分析(5)—(8)式可以发现,直流id中调制信号光的等效F-P光强透过率h′以及交流iΩ中的归一化振幅|A0|和相位ϕ0都是信号光角频率ω的函数,理论上它们都可以作为多普勒频移鉴频参量.这三个参量随频率变化的曲线如图1所示,图中横坐标利用F-P干涉仪的自由光谱范围(free spectral range,FSR)进行了归一化处理,并且采用以坐标原点为参考点的相对频率,原点选择在F-P干涉仪光强透过率峰值位置.

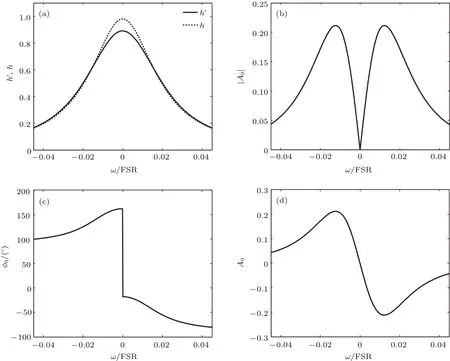
图1 调制信号各参量随频率的变化 (a)h′(ω),h(ω);(b)|A0(ω)|;(c)ϕ0(ω);(d)A0(ω)[16]Fig.1.Curves of modulation signal parameters changing with frequency:(a)h′(ω),h(ω);(b)|A0(ω)|;(c) ϕ0(ω);(d)A0(ω)[16].

在图1(a)中,用实线表示调制信号光等效F-P干涉仪光强透过率h′的频率变化曲线,为了比较,未调整信号光F-P干涉仪光强透过率h的频率变化曲线也在图中用虚线表示.通过观察可以发现,h′(ω)和h(ω)曲线的峰值位置相同,形状相似. 这一特性说明,即使对信号光进行正弦相位调制,其等效F-P干涉仪光强透过率曲线依然能保留未调制情况下的主要特点,可以像边缘技术中利用h(ω)曲线那样[1],利用h′(ω)曲线进行多普勒频移测量.

图1(b)和图1(c)分别为拍频信号iΩ归一化振幅|A0|和相位ϕ0的频率变化曲线.在图1(c)中的原点位置,相位ϕ0(ω)曲线存在一个180°的相位跳变,这就说明在该点振幅A0的符号发生了变化.如果假设当ϕ0为正数时,A0的符号为正A0=|A0|;当ϕ0为负数时,A0的符号为负A0=−|A0|,就可以得到振幅A0的频率变化曲线,如图1(d)所示[17].图1(d)中,在原点两侧,A0曲线存在上、下两个峰,在这两个峰之间存在着一段随频率单调变化的曲线.之前提出的相位调制多普勒频移测量方法就是利用这段A0曲线通过差分的方式测量回波信号光和出射光之间的多普勒频移,即:由于在上、下两个峰之间的频率范围内y=A0(ω)为单调函数,存在反函数如果频率为ω0的出射光经过调制后得到拍频信号振幅测量值y0,频率为ω0+ωd的回波信号光经过调制后得到的测量值y1,则多普勒频移为为了保证最大的多普勒频移测量范围,出射光频率ω0应锁定到这段A0曲线的中间位置,即图1(d)中的原点位置,该点称为多普勒频移测量的工作点[17].所以,图1中的横坐标由于采用以工作点(原点)为参考的相对坐标,本质上反映的是频移量.

2.2 信号处理方法

定义正弦相位调制的周期为TΩ=1/Ω,通过观察(3)式可知,对探测器输出信号i(t)进行积分,当积分时间为T=2nTΩ(n=1,2,3,···)时,交流分量iΩ(t)和i2Ω(t)的积分结果恰好等于零,这样就可以提取出直流分量id:

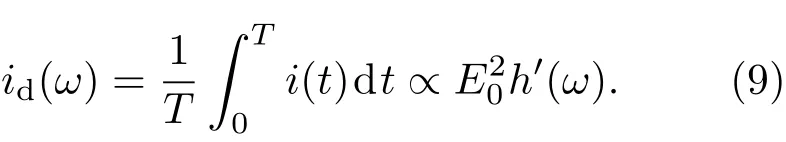
由于正弦相位调制频率Ω已知,很容易产生与拍频信号iΩ(t)同频的两个正交参考信号[21−23]:

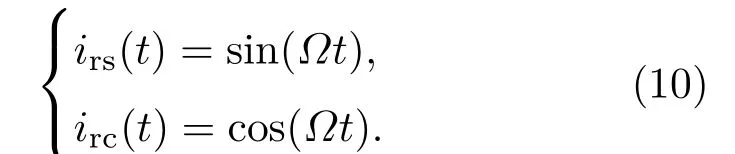
将(10)式中的两个参考信号分别与i(t)进行相关运算[16−18]:

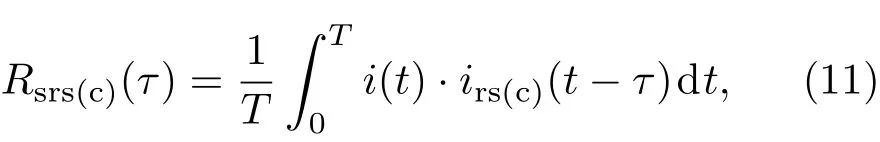
i(t)的三个分量id,iΩ和i2Ω将会分别进行相关运算,当积分时间为T=nTΩ(n=1,2,3,···)时,id和i2Ω的结果恰好为零,则(11)式变为

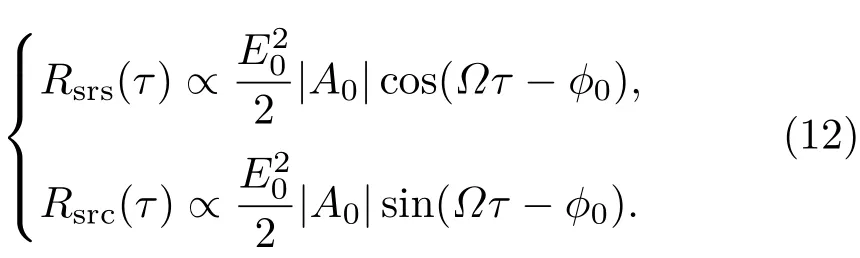
利用(12)式可以得到

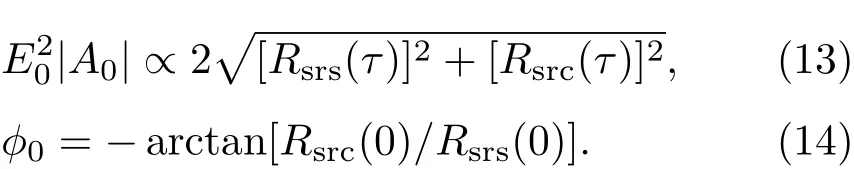
2.3 改进方法

可以采用边缘技术方法,利用h′(ω)曲线进行多普勒频移测量,但要求工作点选择在h′(ω)曲线边缘的中间位置,也就是图1(a)中0.02 FSR点附近[12];也可以采用相位调制方法,利用A0(ω)曲线进行多普勒频移测量,要求工作点选择在A0(ω)曲线中间位置,也就是图1(d)中原点位置.由于需要的工作点位置不同,所以无法简单地同时利用h′(ω)和A0(ω)两条鉴频曲线进行多普勒频移测量.另外,这两种方式都需要额外的探测器对信号光的光强进行测量,不但使系统的结构变得更为复杂,而且也增加了噪声混入的通道.

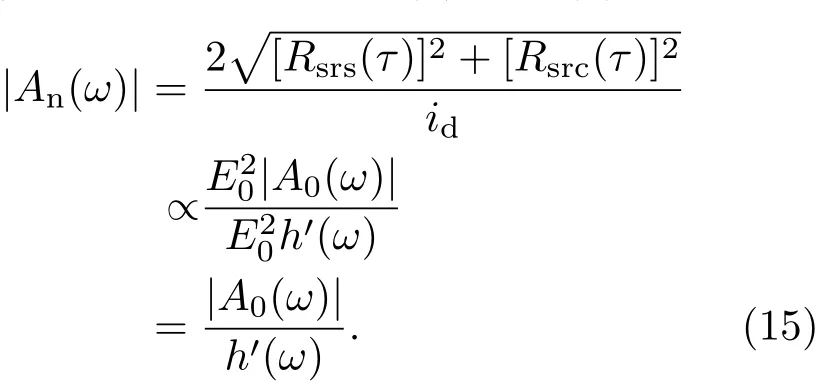
为了能同时利用直流id和交流iΩ中的有用信息,我们定义了一个新的鉴频参量,它的绝对值|An(ω)|可以利用测量值Rsrs(τ),Rsrc(τ)和id获得:可以看到,在利用(15)式定义|An(ω)|的过程中,id和iΩ中信号光强度被同时约掉.这就说明,如果利用An(ω)进行多普勒频移测量,鉴频系统将无需对信号光的光强进行直接测量,间接利用直流id中的光强信息即可,之前与之对应的问题就会得到解决.并且由于新定义的鉴频参量An(ω)是A0(ω)和h′(ω)的函数,所以采用An(ω)进行测量,就是同时利用相位调制信号直流id和交流iΩ中的多普勒频移信息.

另外,可以使用同样的办法利用ϕ0和|An(ω)|获取An(ω),即

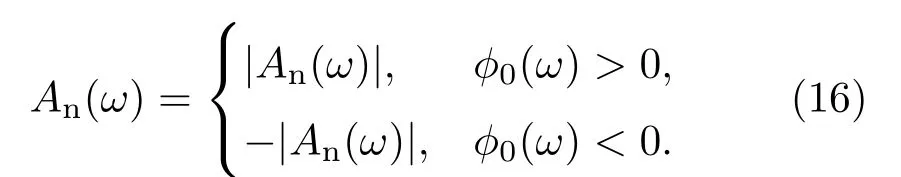
2.4 新鉴频参量An(ω)的理论研究

为了对比,新鉴频参量An以及A0的频移变化曲线用不同的线型在图2(a)中给出.通过观察图2(a)可以看出,An(ω)曲线存在上、下两个峰值,并且峰值间的曲线单调变化并通过原点,总体上与A0(ω)曲线的形状相同.这一性质说明,能够像原相位调制方法中利用A0(ω)曲线那样,利用An(ω)曲线进行多普勒频移测量,包括选择原点作为工作点.但除此以外,An(ω)和A0(ω)曲线也存在一些重要不同点.An(ω)曲线峰-峰值之间的宽度Ln比A0(ω)曲线峰-峰值之间的宽度L0要大;并且An(ω)曲线比A0(ω)曲线更为陡峭.这表明利用An(ω)曲线进行多普勒频移测量将会比利用A0(ω)曲线具有更高的测量动态范围和灵敏度.

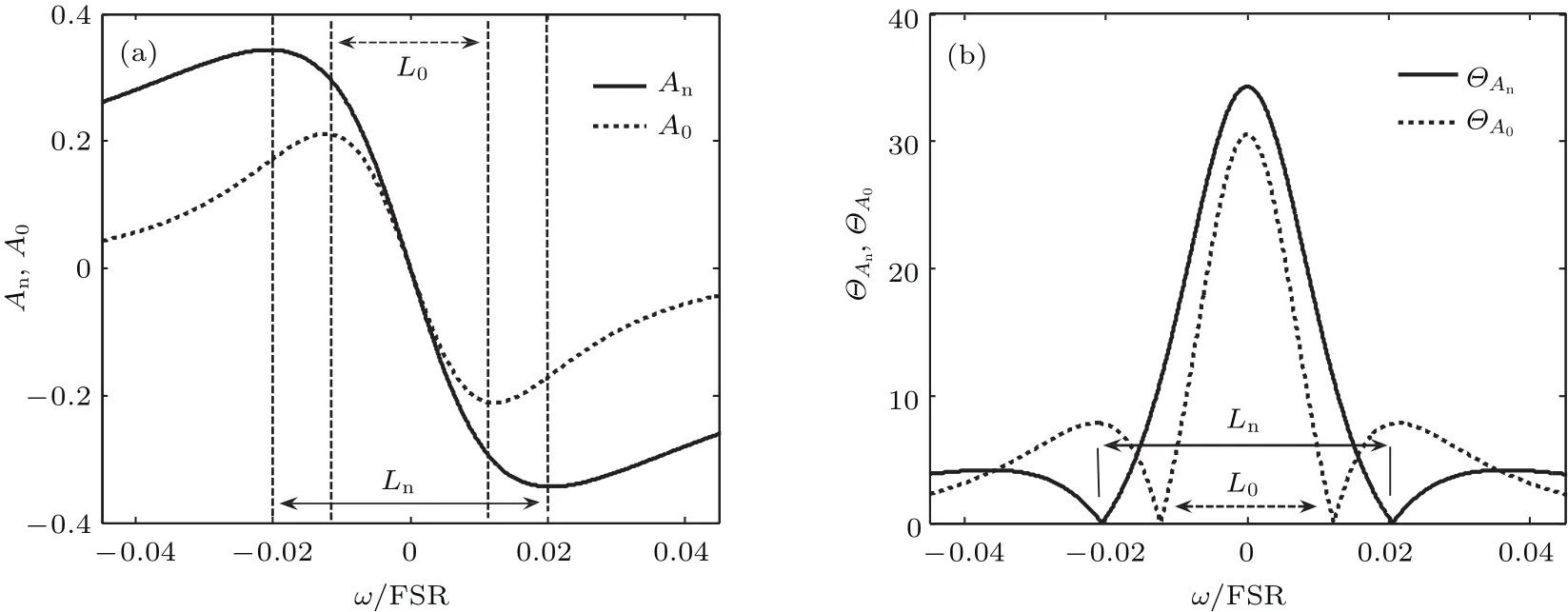
图2 An和A0及其绝对灵敏度ΘAn和ΘA0随频率的变化 (a)An(ω),A0(ω);(b)ΘAn(ω),ΘA0(ω)Fig.2.Curves of An,A0and their absolute sensitivity ΘAnand ΘA0changing with frequency:(a)An(ω),A0(ω);(b) ΘAn(ω),ΘA0(ω).

为了定量地比较利用An(ω)和A0(ω)曲线进行多普勒频移测量的动态范围和灵敏度,它们的绝对灵敏度ΘAn(0)(ω)曲线分别用不同的线型在图2(b)中给出,其中ΘAn(0)(ω)=|dAn(0)(ω)/dω|.如图2(b)所示,ΘAn(ω)和ΘA0(ω)曲线的最大值都出现在工作点(原点)位置,并且随着频移的增大而逐渐降低到零.图2(b)中的ΘAn=ΘA0=0的频移位置与图2(a)中An(ω)和A0(ω)曲线峰值的频率位置相对应,决定了多普勒频移测量的动态范围.An(ω)曲线的多普勒频移范围大于A0曲线的多普勒频移范围并且在此频移测量范围内ΘAn＞ΘA0.

通过定义新的鉴频参量对相位调制多普勒频移测量方法进行改进,本质上就是合理利用调制信号直流分量id中的光强和多普勒频移h′(ω)信息,其既可以保留原相位调制方法的工作方式,又无需对信号光光强进行测量,从而简化了系统结构,减少噪声通道,而且能进一步增加测量动态范围和测量灵敏度.

3 实验研究

3.1 实验装置及其原理

改进后相位调制多普勒频移测量方法的实验研究装置如图3所示.该实验装置由光路和电路两部分组成,在图3中分别用实线和虚线表示,接下来分别对这两部分进行介绍.

该实验装置的光源采用波长为1064 nm的单纵模稳频光纤激光器,其出射光被凸透镜准直后入射到固定目标上.目标的反射信号光再被透镜会聚,并进入多模光纤,由多模光纤引入到鉴频系统中.多模光纤出射的信号光经凸透镜准直后依次经过偏振片、空间光电相位调制器(调整频率为固定值30 MHz),然后再利用分束镜将该信号光分成透射和反射两部分,各占信号光强度的80%和20%.反射光由光电探测器2进行测量,用于监测信号光的光强度.透射光经过×4扩束后垂直入射到固体F-P标准具上,该固体F-P标准具的厚度、表面反射率和表面精细度分别为2 cm,90%和25.最终,该F-P标准具的透射信号光经凸透镜会聚后又由光电探测器1进行测量.

在实验装置的电路部分中,光电探测器1和2输出的信号连接到12位的数据采集卡,该数据采集卡具有一个外触发通道和两个最高采样率为500 MHz的数据通道.为了保证相位调制和数据采集的同步,正弦信号发生器的输出信号被分成两部分,其中一部分经过驱动器放大后连接到相位调整器,对信号光进行正弦相位调制;另一部分连接到数据采集卡的触发通道,作为触发源.将16位模拟量输出卡输出的−5—5 V范围的电压加载到激光器内部的压电陶瓷上,可以使激光器出射光频率在−150—150 MHz范围内线性变化,用于模拟信号光的多普勒频移.另外,可以通过调整激光器内部温度使激光器出射光频率在更大的范围内变化,用于工作点锁定.

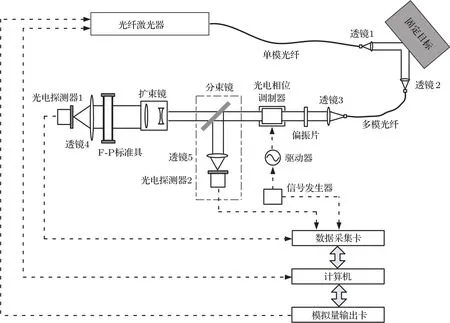
图3 实验研究装置原理图Fig.3.Experimental research device schematic.

需要强调的是,在出射光频率固定的情况下,通过导轨等装置可以使硬目标运动从而产生回波信号光的多普勒频移,但是这种方式不仅增加了实验成本和难度,而且对信号光频移量大小的调节会受到很多的限制,很难实现不同多普勒频移情况下对测量方法各项性质的研究,对多普勒频移测量方法本身的研究并不会产生过多贡献.为了使测量结果能够真实反映目标自身反射等方面的特性,本文对硬目标的反射信号光进行测量;并且在目标位置固定的情况下通过调整出射激光频率来模拟多普勒频移,其效果与目标运动产生的多普勒频移是一样的,而且成本低、实现难度小、频移量可控,对于全面研究多普勒频移测量方法的各项性质具有一定意义.另外,图3中虚线框出的分束镜、凸透镜和光电探测器2,对于改进后的相位调制多普勒频移方法并不是必须的,只是用来对改进前后的方法进行比较.

3.2 实验操作及结果

调整激光器内部温度,使出射光的频率ω0落在F-P标准具某一透过率峰位置,该点对应频移测量的工作点.当激光器内部温度达到平衡后,打开光电相位调制器,并控制模拟量输出卡,使其输出电压从−5 V到+5 V按照0.1 V的步长线性变化,从而使激光器的输出光频率从ω0+150 MHz到ω0−150 MHz按3 MHz的步长变化.在每次出射光频率改变后,数据采集卡同时以500 MHz的采样率对光电探测器1和2输出的信号进行采样,各采集500个点.然后,利用(9)—(14)式对光电探测器1的采样数据进行计算,获得直流信号以及拍频信号的振幅和相位ϕ0;对光电探测器2的采样数据进行平均运算获得信号光强这样就获得了不同频率下,ϕ0以及的测量值,如图4(a)—(d)所示.图4中的横坐标仍然使用以原点(工作点)为参考的相对频率坐标来表示频移,接下再利用图4中的数据获取鉴频参量A0和An.

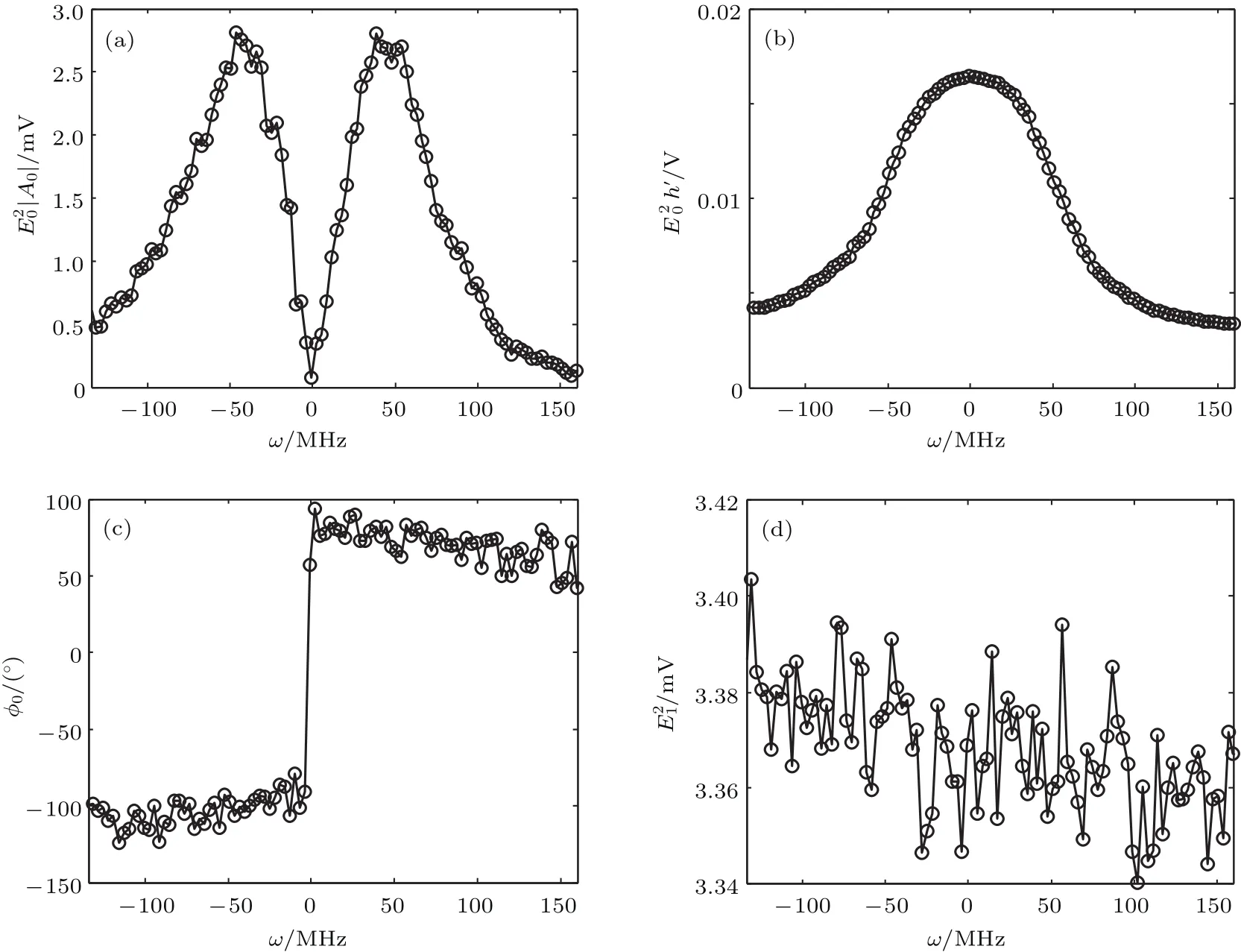
图4 不同频移下|A0|,h′,ϕ0和的测量值 (a)|A0(ω)|;(b)h′(ω);(c)ϕ0(ω);(d)Fig.4.Measuring values of |A0|,h′, ϕ0and under different frequency shifts:(a)|A0(ω)|;(b)h′(ω);(c) ϕ0(ω);(d).

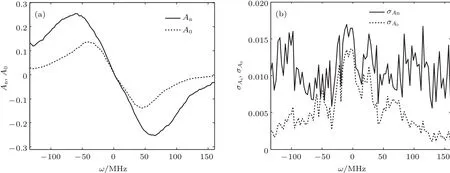
图5 A0和An的(a)测量平均值和(b)标准偏差曲线Fig.5.(a)Measurement mean values and(b)standard deviation curves of A0and An.

在每个频移位置,都对A0和An进行了多次测量并计算平均值和标准偏差,然后分别利用不同的线型在图5(a)和图5(b)表示出来.

通过比较图5(a)和图2(a)可以看出,实际测量的An(ω)和A0(ω)曲线与理论计算的曲线很相似,这可以证明理论分析的正确性.通过观察图5(b)可以看到An的测量标准偏差σAn大于A0的测量标准偏差σA0. 根据误差传递理论,σAn＞σA0的主要原因是h′的测量标准偏差大于的测量标准偏差.然而,h′和的测量标准偏差又主要依赖它们各自散粒噪声功率密度的大小

利用数值计算方法对图5(a)中A0(ω)和An(ω)的测量曲线进行偏微分运算,可以获得多普勒频移测量的绝对灵敏度ΘA0(ω)和ΘAn(ω)曲线,如图6(a)所示.通过观察图6(a)中的测量曲线可以发现,An的多普勒频移测量动态范围(大约为−54—62 MHz)大于A0的多普勒频移测量动态范围(大约为−36—43 MHz),并且在整个测量动态范围内ΘAn(ω)＞ΘA0(ω),这与图2(b)中的理论曲线具有同样的分布规律.利用绝对灵敏度ΘA0(n)(ω)曲线、测量标准偏差σAn(0)(ω)曲线以及计算公式σνA0(n)=1/(σA0(n)ΘA0(n))可以获得多普勒频移测量标准偏差σνA0(n)(ω)曲线,如图6(b)所示.通过观察多普勒频移测量标准偏差σνA0(ω)和σνAn(ω)的曲线分布,可以发现大约在−20—25 MHz较小的频移范围内,测量标准偏差σνA0和σνAn基本相同,但是大约在−48—−20 MHz以及25—52 MHz较大的频移范围内,σνAn变得小于σνA0,这证明利用An进行多普勒频移测量总体上比利用A0具有更高的测量精度.

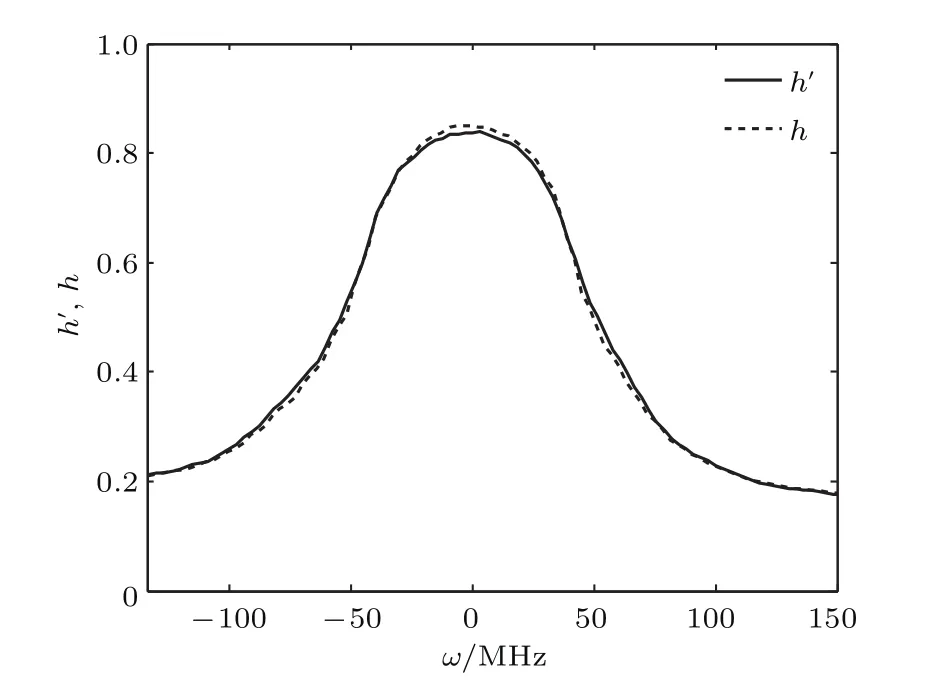
图7 h′(ω)和h(ω)测量平均值曲线Fig.7.Measuring mean value curves of h′(ω)and h(ω).

3.3 全功率实验结果

虽然,上面的实验结果可以在测量精度和动态范围方面展现An的优势,但并不充分,因为在获取An参量的过程中只使用了信号光的部分光功率,另外的功率部分则被用于测量信号光光强,信号光的功率大小是影响测量精度的重要因素.在实际测量过程中,无需对信号光的光强进行测量,所以为了更好地展现An的优势,图3虚框中的分束镜、透镜以及光电探测器被移除,使信号光的全部功率通过相位调制器,然后重复以上的实验过程,来获得不同频率下的E2h′′,E2|A′0|和ϕ′0. 新的实验结果用黑色圆圈分别在图8(a)—(c)给出.为了进一步反映测量精度和动态范围的提高程度,之前的测量结果h′,|A0|和ϕ0也分别在图8(a)—(c)给出.

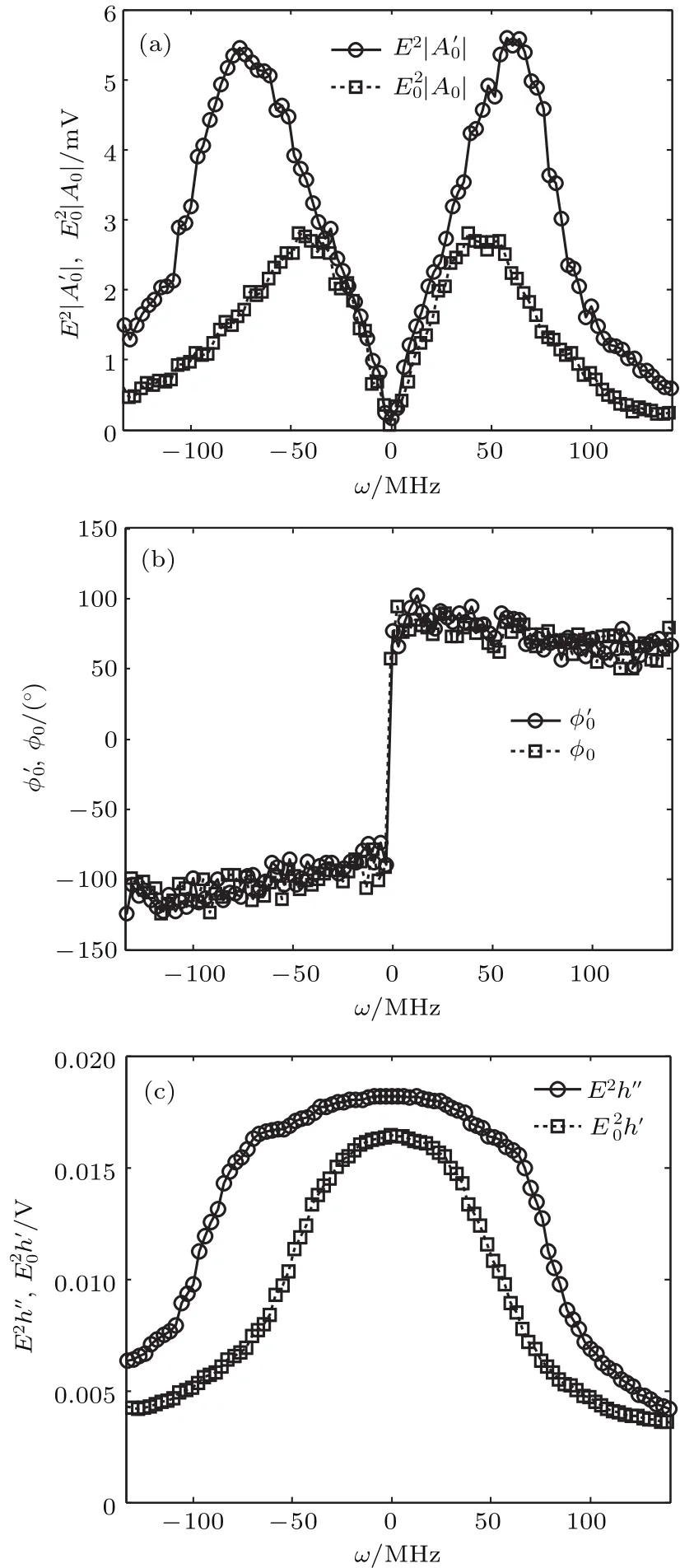
图 8 不同频率下 E2|A′0|(|A0|), ϕ′0(ϕ0) 和 E2h′′(h′)的 测 量 值 (a)E2|A′0(ω)| 和 |A0(ω)|;(b) ϕ′0(ω) 和 ϕ0(ω);(c)E2h′′(ω) 和 h′(ω)Fig.8.Measuring values of E2|A′0|(|A0|), ϕ′0(ϕ0)and E2h′′(h′)under different frequency shifts:(a)E2|A′0(ω)|,|A0(ω)|;(b) ϕ′0(ω),ϕ0(ω);(c)E2h′′(ω),h′(ω).

根据前面的理论可知,由于相位调制和F-P干涉仪等实验参数没有发生变化,所以在去除光强探测器后,调制信号光的F-P干涉仪光强透过率以及相位调制拍频信号的归一化振幅和相位不会发生变化,即h′′=h′,A′0=A0和ϕ′0=ϕ0. 然而,由于在两次实验中,信号光的光强E2和发生了变化(E2=+即E2＞),所以有E2h′′＞h′和E2|A′0|＞|A0|,如图8所示.

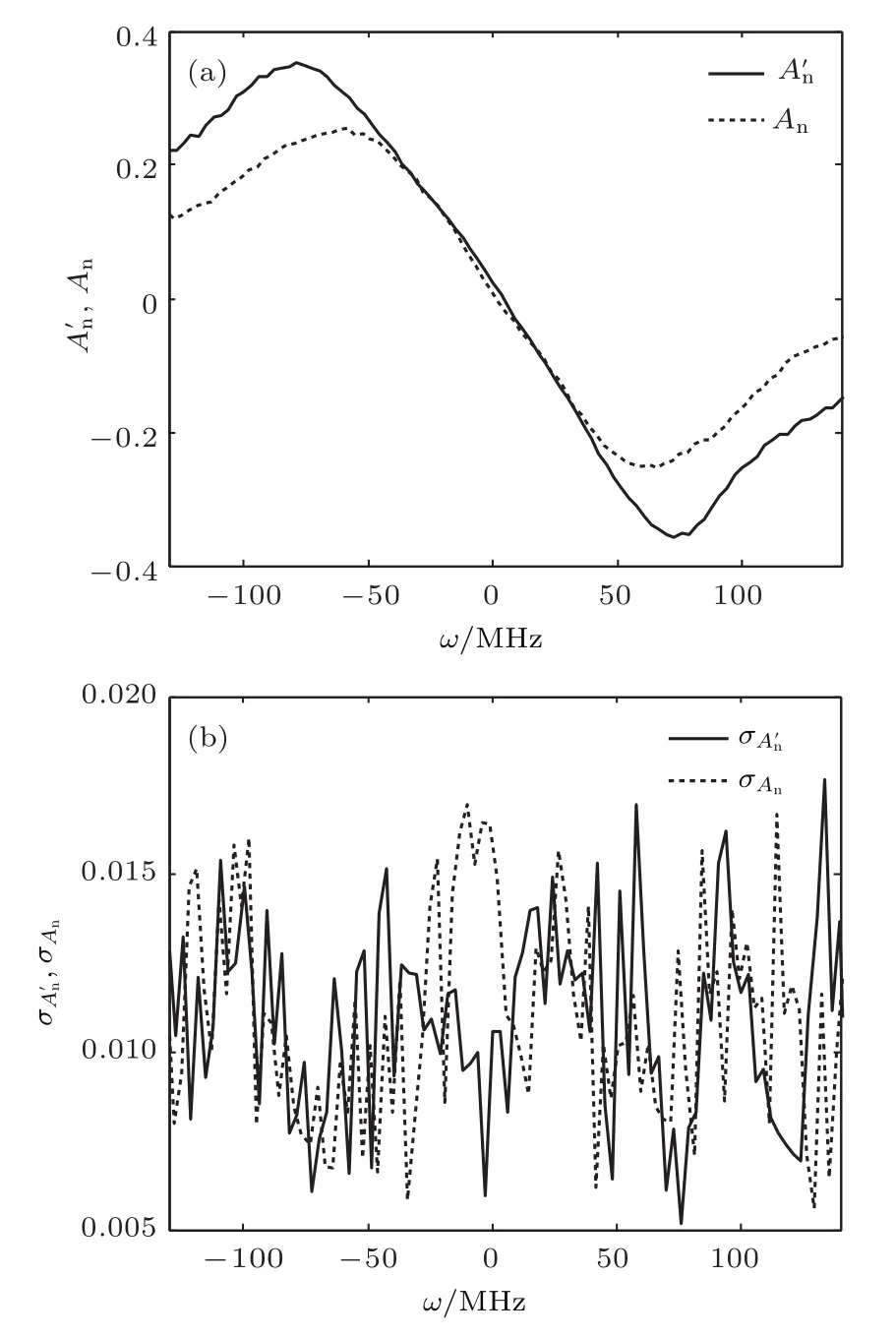
图9 A′n和An的(a)测量平均值和(b)标准偏差曲线Fig.9.(a)Curves of measurement mean values and(b)standard deviation of A′nand An.

根据前面的分析,去掉光强探测器前、后两次实验测量的A′n(ω)和An(ω)曲线的形状应该基本相同.然而,通过观察图9(a)和图10(a),可以发现A′n(ω)曲线上、下峰之间的高度差和横向距离都要比An(ω)曲线的要大,但斜率却基本相同,即A′n(ω)曲线的多普勒频移测量范围−90—80 MHz比An曲线的−54—62 MHz要大,但它们最高可达到的多普勒频移测量灵敏度基本相同,这一实验结果与理论不符.产生这一现象的可能原因是光电探测器对不同强度的信号光的响应不够线性.通过观察图10(b)可以发现,在多普勒频移测量范围内,的多普勒频移测量标准偏差σνA′n总体上比An的多普勒频移测量标准偏差σνAn小得多.图10中的实验结果说明,通过移除光强探测器,使信号光的全部光功率进入相位调制多普勒频移测量系统,将会进一步提高多普勒频移测量的动态范围和灵敏度.

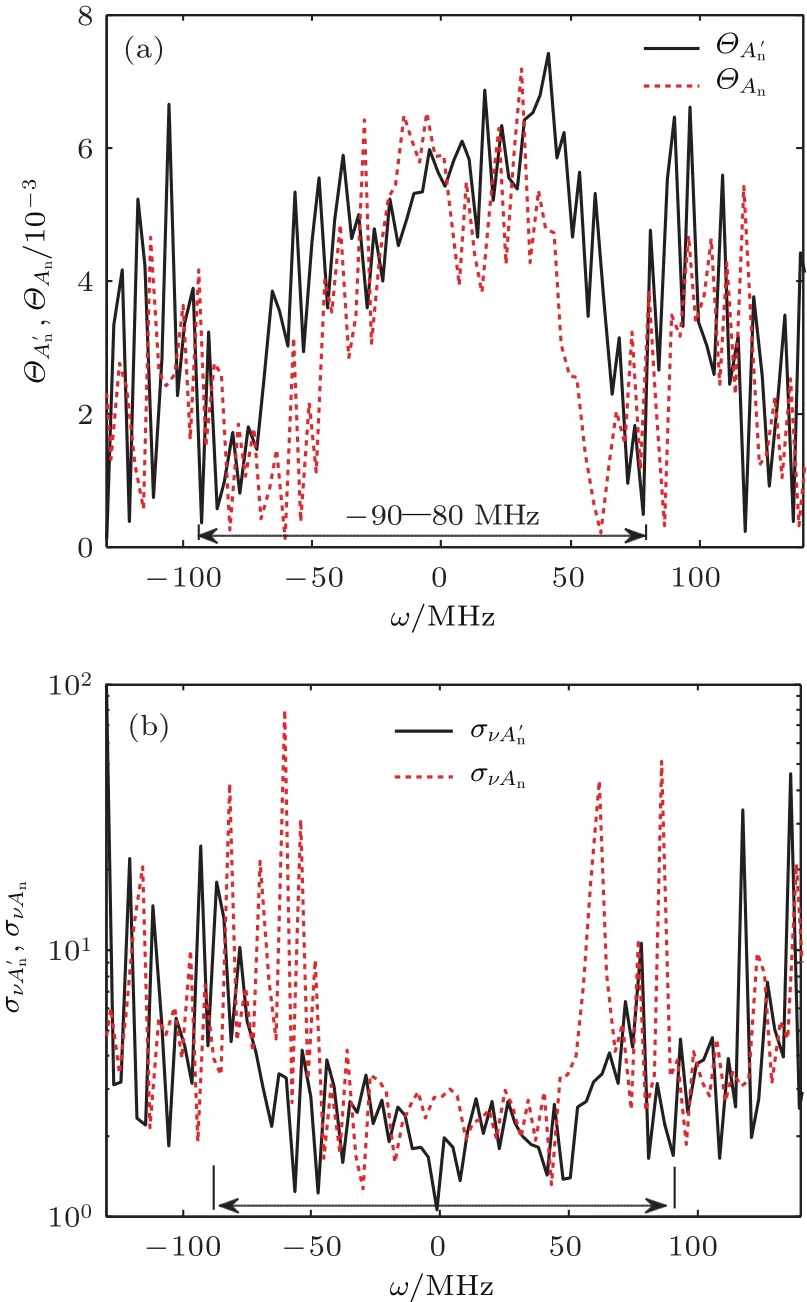
图10 多普勒频移测量灵敏度和标准偏差曲线(a) ΘA′n(ω)和 ΘAn(ω);(b)σνA′n(ω)和 σνAn(ω)Fig.10.Curves of Doppler shift measuring sensitivity and standard deviation:(a) ΘA′n(ω)and ΘAn(ω);(b) σνA′n(ω)and σνAn(ω).

通过进一步计算图6和图10中A0和A′n的实验数据,可以发现,与A0相比,利用A′n进行多普勒频移测量的动态范围提高接近一倍,可到达的最小测量标准偏差约降低35%.

4 结 论

相位调制信号直流分量中包含了光强信息和多普勒频移信息,但之前提出的相位调制多普勒频移测量方法并没有对其加以利用,造成了有效信息的浪费.所以本文对原有相位调制多普勒频移测量方法进行了改进,使其可以合理地利用相位调制信号直流分量中的有用信息.改进后的相位调制多普勒频移测量方法无需光强探测器,不但系统结构得到了简化,而且减少噪声混入通道.实验结果证明,其测量动态范围提高约一倍,测量精度提高约35%.

[1]Xia H,Dou X,Sun D,Shu Z,Xue X,Han Y,Hu D,Han Y,Cheng T 2012Opt.Express20 15286

[2]Du Z H,Li S Q,Jiang C Z,Tao Z F,Gao H,Xie Y 2004Acta Opt.Sin.24 834(in Chinese)[杜振辉,李淑清,蒋诚志,陶知非,高华,谢艳2004光学学报24 834]

[3]Yan C H,Wang T F,Zhang H Y,Lü T,Wu S S 2017Acta Phys.Sin.66 234208(in Chinese)[晏春回,王挺峰,张合勇,吕韬,吴世松2017物理学报66 234208]

[4]Tang L,Shu Z F,Dong J H,Wang G C,Wang Y T,Xu W J,Hu D D,Chen T D,Dou X K,Sun D S,Cha H 2010Chin.Opt.Lett.8 726

[5]Wen F,Ye H,Zhang X,Wang W,Li S,Wang H 2017Photon.Res.5 676

[6]Li Y C,Wang C H,Qu Y,Gao L,Chong H,Yang Y,Gao J,Wang A 2011Chin.Phys.B20 014208

[7]Li Y C,Wang C H,Gao L,Cong H F,Qu Y 2012Acta Phys.Sin.61 044207(in Chinese)[李彦超,王春辉,高龙,从海芳,曲杨2012物理学报61 044207]

[8]Bai Y,Ren D M,Zhao W,Qu Y,Qian L,Chen Z 2012Opt.Express20 764

[9]Bai Y,Ren D M,Zhao W,Qian L,Chen Z,Liu Y 2010Appl.Opt.49 4018

[10]Li Y C,Wang Y Q,Liu C Y,Yang J R,Ding Q 2016Appl.Phys.B122 24

[11]Fang S,Bi Z Y,Yao Y 2015Chin.Phys.B24 074202

[12]Li C Q,Wang T F,Zhang H Y,Xie J J,Liu L S,Guo J 2016Acta Phys.Sin.65 084206(in Chinese)[李成强,王挺峰,张合勇,谢京江,刘立生,郭劲 2016物理学报 65 084206]

[13]Xia H,Sun D,Yang Y,Shen F,Dong J,Kobayashi T 2007Appl.Opt.46 7120

[14]Imaki M,Kobayashi T 2005Appl.Opt.44 6023

[15]Du J,Ren D M,Zhao W J,Qu Y C,Chen Z L,Geng L J 2013Chin.Phys.B22 024211

[16]Shen F H,Shu Z F,Sun D S,Wang Z C,Xue X H,Chen T D,Dou X K 2012Acta Phys.Sin.61 030702(in Chinese)[沈法华,舒志峰,孙东松,王忠纯,薛向辉,陈廷娣,窦贤康2012物理学报61 030702]

[17]Du J,Zhao W J,Qu Y C,Chen Z L,Geng L J 2013Acta Phys.Sin.62 184206(in Chinese)[杜军,赵卫疆,曲彦臣,陈振雷,耿利杰2013物理学报62 184206]

[18]Qu Y C,Du J,Zhao W J,Geng L J,Liu C,Zhang R L,Chen Z L 2014Acta Photon.Sin.34 1112001(in Chinese)[曲彦臣,杜军,赵卫疆,耿利杰,刘闯,张瑞亮,陈振雷2014光子学报34 1112001]

[19]Du J,Qu Y C,Zhao W J,Geng L J,Liu C,Zhang R L,Chen Z L 2014Acta Opt.Sin.34 0712001(in Chinese)[杜军,曲彦臣,赵卫疆,耿利杰,刘闯,张瑞亮,陈振雷 2014光学学报34 0712001]

[20]Eric D B 2001Am.J.Phys.69 79

[21]Zhao L,Tian X J,Liang L,Zheng C T,Wang Y D 2012J.Jilin Univ.30 5(in Chinese)[赵玲,田小建,梁磊,郑传涛,王一丁2012吉林大学学报30 5]

[22]Zheng Z,Zhao C,Zhang H,Yang S,Zhang D,Yang H,Liu J 2016Opt.Laser Technol.80 169

[23]Yang H Z,Zhao C M,Zhang H Y,Yang S H,Li C 2017Acta Phys.Sin.66 184201(in Chinese)[杨宏志,赵长明,张海洋,杨苏辉,李晨2017物理学报66 184201]